具有输入约束的电机伺服系统鲁棒位置控制器的实现方法与流程

本发明涉及一种控制器，具体涉及一种具有控制输入约束的电机伺服系统非线性鲁棒位置控制器，属于机电伺服控制领域。

背景技术：

电机伺服系统由于具有响应快、传动效率高、维护方便以及能源获取方便等突出优点，广泛应用于工业及国防等重要领域，如机床进给、火箭炮随动系统、机器人等。随着这些领域的发展和技术水平的不断进步，迫切需要高性能的电机伺服系统作为支撑，传统基于线性化方法得到的控制性能逐渐不能满足系统需求。电机伺服系统存在诸多模型不确定性，包括参数不确定性(如负载质量的变化、随温度及磨损而变化的粘性摩擦系数等)以及不确定性非线性(如外干扰等)，这些不确定性的存在可能会严重恶化期望的控制性能，甚至使基于系统名义模型所设计的控制器不稳定，同时系统的控制输入可能遭受饱和行为，因此成为发展先进控制器的主要障碍。而且对于现有电机伺服系统的建模往往不够充分比如忽略摩擦的影响或者简单的把摩擦模型建立为线性的，然而存在于电机伺服系统中的摩擦对系统的高精度运动控制有着重要的影响，会引起极限环振荡、粘滑运动等现象，因此需要对电机伺服系统的建模作进一步研究。

为了处理以上存在的问题，有学者提出了连续的饱和自适应鲁棒控制算法(SARC)能对系统中存在的模型不确定性以及执行器中固有的饱和行为进行有效地控制，并获得了一致有界跟踪(即跟踪误差有界)的结果，这样的性能可能会在实际高精度需求的场合难以满足要求。为了获得渐近跟踪性能， 有学者针对一类具有模型不确定性的二阶系统提出了饱和的基于误差符号积分鲁棒的控制算法，然而这种算法只能保证整个系统半全局渐近稳定，并且设计控制器及证明稳定性时相对复杂。如何恰当的设计出能保证整个系统全局渐近稳定同时使控制输入具有约束性以避免控制输入饱和行为的发生并且简单的控制器仍是目前研究的焦点。

总结来说，现有考虑电机伺服系统饱和的控制策略的不足之处主要有以下几点：

1.对电机伺服系统建模不充分。电机伺服系统的建模不确定性主要有非线性摩擦和未建模扰动等。存在于电机伺服系统中的摩擦会引起极限环振荡、粘滑运动等不利因素，对系统的高精度运动控制有着重要的影响。同时，实际的电机伺服系统不可避免的会受到外界负载的干扰，若忽略将会降低系统的跟踪性能；

2.饱和自适应鲁棒控制算法(SARC)对同时存在参数不确定性和不确定性非线性的系统只能保证跟踪误差有界(即保证跟踪误差在一个有界的范围内，并不能确保跟踪误差趋于零)，这样的性能可能会在实际高精度需求的场合难以满足要求；

3.饱和的基于误差符号积分的鲁棒控制器设计及稳定性证明相对复杂并且只能保证整个系统半全局渐近稳定。

技术实现要素：

本发明为解决现有电机伺服系统的建模不够充分、饱和自适应鲁棒控制算法(SARC)对同时存在参数不确定性和不确定性非线性的系统只能保证跟踪误差有界(即保证跟踪误差在一个有界的范围内，并不能确保跟踪误差趋于零)，同时饱和的基于误差符号积分的鲁棒控制器设计及稳定性证明相对复 杂并且只能保证整个系统半全局渐近稳定的问题，提出一种具有控制输入约束的电机伺服系统非线性鲁棒位置控制器。

本发明为解决上述问题采取的技术方案是：

1、一种具有输入约束的电机伺服系统鲁棒位置控制器的实现方法，其特征在于，该方法包括以下步骤：

步骤一、建立电机位置伺服系统的数学模型，根据牛顿第二定律可得系统的运动学方程为：

公式(1)中，m为惯性负载参数，y为惯性负载角位移，k_f为与输入电压有关的力矩常数，u为系统的控制输入，B为粘性摩擦系数，为可建模的非线性摩擦模型，为不确定性项，包括外干扰及未建模的摩擦。

选取连续静态非线性摩擦模型为：

公式(2)中a₁、a₂、a₃、b₁、b₂均为已知常数，tanh函数为双曲正切函数；此连续静态摩擦模型的特征如下：①此摩擦模型是关于时间连续可微并且关于原点对称的；②库伦摩擦特性可用表达式表征；③静态摩擦系数可用b₁+b₂的值来近似表示；④表达式表征Stribeck效应；

公式(2)中的连续可微tanh(v₁)函数关于它的变量v₁满足：

选取状态变量为：则电机位置伺服系统的运动学方程转化为如下状态方程形式：

y＝x₁

公式(4)中θ₁＝m/k_f，θ₂＝b₁/k_f，θ₃＝b₂/k_f，θ₄＝B/k_f，定义参数集θ＝[θ₁,θ₂,θ₃,θ₄]^T；S_f(x₂)＝tanh(a₁x₂)，P_f(x₂)＝tanh(a₂x₂)-tanh(a₃x₂)，其中参数θ₁、θ₂、θ₃、θ₄均为名义值且已知，任何参数偏差造成的不确定性以及模型不确定性影响都可归结到系统的总干扰Δ(x,t)＝d(x,t)/m中；

假设1：系统状态x₁、x₂可测；

假设2：总扰动Δ(x,t)足够光滑并且其中η₁为已知常数；

步骤二、针对公式(4)中的状态方程，设计具有控制输入约束的电机伺服系统非线性鲁棒位置控制器，其具体步骤如下：

步骤二(一)、定义一组类似开关函数的变量为：

公式(5)中z₁＝x₁-x_1d为系统的跟踪误差，k₁、k₂为正反馈增益；在公式(5)中引入了一个扩张的误差信号z₃来获得额外的设计自由；

步骤二(二)、设计具有约束且基于期望指令补偿的非线性鲁棒控制器输入u，使得电机伺服系统具有全局渐近跟踪性能

根据公式(5)，扩张误差信号z₃变换为：

基于系统状态方程(4)，可以得到：

其中：

根据公式(7)的结构，具有控制输入约束的电机伺服系统非线性鲁棒位置控制器可以设计为：

q_s＝k₂z₂(θ₁k₁+θ₁k₂-θ₄)-k₁(θ₄-θ₁k₁)(z₂-k₁z₁),

q_n＝-η₂sign(z₃)

公式(9)中ω为正常数，同时还可以看出控制输入u具有约束性，并且u的上界为ω，即u≤ω，可通过调节ω来控制u的大小；q_a为基于模型的前馈补偿控制律；q_s为鲁棒控制律用来保证名义系统的稳定性；q_n为基于扩张误差符号z₃的鲁棒控制律，其用来处理时变的扰动；其中sign(z₃)定义为：

由于信号z₃未知，为了计算sign(z₃)，定义函数g₀(t)为：

由于z₃(t)＝lim_τ→0(g₀(t)-g₀(t-τ))/τ，τ可以选取为采样时间，根据(9)，只需要知道z₃的符号sign(z₃)即可，因此只需要知道g(t)增加还是减小就可以获得sign(z₃)，其中sign(z₃)＝sign(g₀(t)-g₀(t-τ))；

对公式(7)进行微分并经过转化可以得到：

根据公式(3)以及中值定理可以推出：

从而可以进一步得到：

公式(14)中γ₁、γ₂、γ₃为正常数；

把(9)中的控制律带入到(12)中，可以得到：

步骤三、选取恰当的正常数τ(τ＞0)、ω(ω＞0)、k₁(k₁＞0)、k₂(k₂＞0)以及η₂(η₂＞0)，从而来确保整个系统稳定，并使电机位置伺服系统的控制输入u具有约束性同时位置输出y(t)能准确地跟踪期望的位置指令y_d(t)。

本发明的有益效果是：本发明选取直流旋转电机位置伺服系统作为研究对象，建立了充分考虑系统的摩擦以及其它扰动的非线性模型；所设计的控制器通过引入基于期望指令轨迹的连续摩擦模型前馈补偿项针对系统存在的摩擦具有良好的补偿效果；所设计的控制器通过引入基于扩张误差信号积分的鲁棒项针对系统存在的外部干扰以及其它未建模动态等不确定性具有良好的鲁棒性；所设计的控制器的控制输入具有约束性，并能通过调节控制输入的大小来避免控制输入饱和行为的发生；所设计的控制器为全状态反馈控制器，并能使电机伺服系统的位置输出具有全局渐近跟踪性能，即当时间趋于无穷时跟踪误差为零；所设计的控制器参数容易调节并且控制输入电压连续，更利于在工程实际中应用。仿真结果验证了其有效性。

附图说明

图1是本发明所考虑的直流旋转电机位置伺服系统示意图。

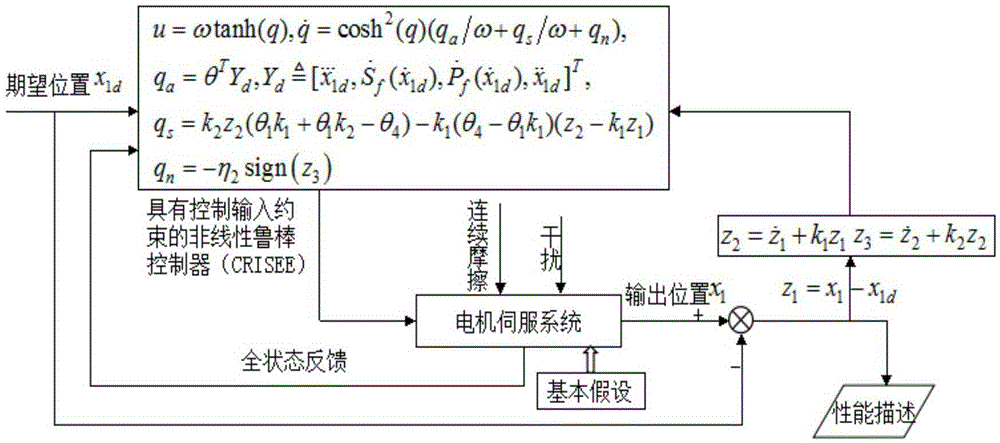
图2是具有控制输入约束的电机伺服系统非线性鲁棒位置控制器原理示意及流程图。

图3是本发明所设计的控制器(图中以CRISEE标识，其控制输入约束 幅值为2.5V)和传统PID控制器(图中以PID标识)分别作用下系统的跟踪误差随时间变化的曲线。

图4是电机位置伺服系统的实际控制输入u随时间变化的曲线。

具体实施方式

结合图1至图2说明本实施方式，本实施方式所述一种具有控制输入约束的电机伺服系统非线性鲁棒位置控制器的设计方法具体步骤如下：

步骤一、建立电机位置伺服系统的数学模型，本发明以直流旋转电机(如图1所示)为例，根据牛顿第二定律可得系统的运动学方程为：

公式(1)中m为惯性负载参数，y为惯性负载角位移，k_f为与输入电压有关的力矩常数，u为系统的控制输入，B为粘性摩擦系数，为可建模的非线性摩擦模型，为外干扰及未建模的摩擦等不确定性项。

选取连续静态非线性摩擦模型为：

公式(2)中a₁、a₂、a₃、b₁、b₂均为已知常数，tanh函数为双曲正切函数。此连续静态摩擦模型的主要特征如下：①此摩擦模型是关于时间连续可微并且关于原点对称的；②库伦摩擦特性可用表达式表征；③静态摩擦系数可用b₁+b₂的值来近似表示；④表达式可以表征Stribeck效应。

公式(2)中的连续可微tanh(v₁)函数关于它的变量v₁具有以下特点：

选取状态变量为：则电机位置伺服系统的运动学方程 可以转化为如下状态方程形式：

y＝x₁

公式(4)中θ₁＝m/k_f，θ₂＝b₁/k_f，θ₃＝b₂/k_f，θ₄＝B/k_f，定义参数集S_f(x₂)＝tanh(a₁x₂)，P_f(x₂)＝tanh(a₂x₂)-tanh(a₃x₂)。其中参数θ₁、θ₂、θ₃、θ₄均为名义值且已知，任何参数偏差造成的不确定性以及模型不确定性影响都可归结到系统的总干扰Δ(x,t)＝d(x,t)/m中。

假设1：系统状态x₁、x₂可测；

假设2：总扰动Δ(x,t)足够光滑并且其中η₁为已知常数。

在以下的控制器设计中，假设2给未建模扰动施加了一些约束。虽然摩擦一般被建模为不连续函数会导致假设2有点保守，但是没有哪个执行器可以产生不连续的力来补偿不连续摩擦力的影响。本发明在进行基于模型的控制器设计时采用连续的摩擦模型，因而假设2符合实际情况。控制器的设计目标是使位置输出x₁尽可能地跟踪期望跟踪的轨迹x_1d＝y_d(t)。

步骤二、针对公式(4)中的状态方程，设计具有控制输入约束的电机伺服系统非线性鲁棒位置控制器，其具体步骤如下：

步骤二(一)、定义一组类似开关函数的变量为：

公式(5)中z₁＝x₁-x_1d为系统的跟踪误差，k₁、k₂为正反馈增益。我们在公式(5)中引入了一个扩张的误差信号z₃来获得额外的设计自由。但是，由于扩张的误差信号z₃依赖于加速度的信息从而使得它不可测，这里仅仅用来协助以下的控制器设计。

步骤二(二)、设计具有约束且基于期望指令补偿的非线性鲁棒控制器输 入u，使得电机伺服系统具有全局渐近跟踪性能。

根据公式(5)，扩张误差信号z₃可以整理为：

基于系统状态方程(4)，我们可以得到：

其中：

根据公式(7)的结构，具有控制输入约束的电机伺服系统非线性鲁棒位置控制器可以设计为：

q_s＝k₂z₂(θ₁k₁+θ₁k₂-θ₄)-k₁(θ₄-θ₁k₁)(z₂-k₁z₁),

q_n＝-η₂sign(z₃)

公式(9)中ω为正常数，同时还可以看出控制输入u具有约束性，并且u的上界为ω，即u≤ω，我们可以通过调节ω来控制u的大小；q_a为基于模型的前馈补偿控制律；q_s为鲁棒控制律用来保证名义系统的稳定性；q_n为基于扩张误差符号z₃的鲁棒控制律，其用来处理时变的扰动；其中sign(z₃)定义为：

由于信号z₃未知，为了计算sign(z₃)，定义函数g₀(t)为：

由于z₃(t)＝lim_τ→0(g₀(t)-g₀(t-τ))/τ，τ可以选取为采样时间，根据(9)可以看出我们只需要知道z₃的符号sign(z₃)即可，因此我们只需要知道g(t)增 加还是减小就可以获得sign(z₃)，其中sign(z₃)＝sign(g₀(t)-g₀(t-τ))，这样看来，获得sign(z₃)并不需要加速度的信息，从而比获得z₃容易多了。

对公式(7)进行微分并经过转化可以得到：

为了下面的稳定性分析，根据公式(3)以及中值定理可以推出：

从而可以进一步得到：

公式(14)中γ₁、γ₂、γ₃为正常数。

把(9)中的控制律带入到(12)中，我们可以得到：

步骤三、选取恰当的正常数τ(τ＞0)、ω(ω＞0)、k₁(k₁＞0)、k₂(k₂＞0)以及η₂(η₂＞0)，从而来确保整个系统稳定，并使电机位置伺服系统的控制输入u具有约束性同时位置输出y(t)能准确地跟踪期望的位置指令y_d(t)。

本例子中，还基于Lyapunov方程分析了基于控制器(9)作用下的电机位置伺服系统的稳定性：

理论1：选取足够大的反馈增益k₁、k₂，使得以下定义的矩阵Λ正定，同时确保ωη₂≥η₁，那么提出的控制律(9)能够确保整个闭环电机伺服系统的所有信号有界，并且能获得全局渐近跟踪性能，即当t→∞时z₁→0。Λ定义为：

其中k₃为：

k₃＝θ₄-θ₁k₁-θ₁k₂ (17)

选取Lyapunov方程为：

对公式(18)关于时间进行求导可得：

把公式(5)和(15)代入公式(19)，可得：

由于ωη₂≥η₁，可得：

再根据公式(14)，可对公式(20)进一步转化得：

根据公式(16)中定义的Λ为正定矩阵，对公式(22)进一步转换可得：

公式(23)中z定义为z＝[z₁,z₂,z₃]^T；λ_min(Λ)为矩阵Λ的最小特征值。

根据公式(23)可以得到V∈L_∞以及W∈L₂，同时信号z有界。因此，可以得出x以及控制输入u有界。基于z₁、z₂以及z₃的动态方程，可以得到W的时间导数有界，因此W一致连续。从而，根据Barbalat引理可以得到当t→∞时W→0，理论1即得到证明。

具有控制输入约束的电机伺服系统非线性鲁棒位置控制器原理示意及流程如图2所示。

下面结合一个具体的例子来说明前述实施例的实现：

电机伺服系统参数为：惯性负载参数m＝0.4kg·m²；力矩放大系数k_f＝4N·m/V；粘性摩擦系数B＝1.6N·m·s/rad；连续摩擦模型中的参数：a₁＝700、a₂＝15、a₃＝1.5、b₁＝0.1、b₂＝0.05；时变外干扰d(t)＝2sin(t)N·m，因此选取η₁＝2；系统期望跟踪的位置指令为曲线x_1d(t)＝sin(πt)[1-exp(-t³)]rad。

本发明所设计的控制器的参数选取为:τ＝0.2ms、k₁＝250、k₂＝10以及η₂＝1,控制输入约束幅值选取为w＝2.5；PID控制器参数选取为：P增益k_P＝1500,I增益k_I＝800,D增益k_D＝10。

控制器作用效果：图3是本发明所设计的控制器(图中以CRISEE标识)和传统PID控制器(图中以PID标识)分别作用下系统的跟踪误差随时间变化的曲线，从图中可以看出，本发明所设计的控制器作用下系统的跟踪误差明显小于PID控制器作用下系统的跟踪误差并且稳态跟踪误差趋近于0，从而使其跟踪性能获得很大的提高。

图4是电机位置伺服系统的控制输入u随时间变化的曲线，从图中可以看出，本发明所得到的控制输入信号连续而且有规律，同时控制输入幅值约束在2.5V内，能有效避免控制输入饱和行为的发生，有利于在工程实际中应用。