一种UPFC控制器间交互影响的规范型评估方法与流程

本发明涉及一种UPFC控制器间交互影响的规范型评估方法，属于电力系统控制技术。
背景技术：
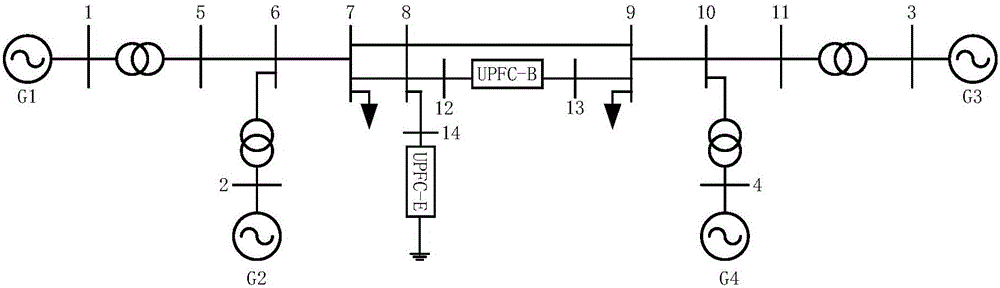
：统一潮流控制器(UnifiedPowerFlowController，UPFC)通常是由两个电压源型换流器(VSC)组成的，它们共用一个直流电容，一侧通过耦合变压器并联到母线上，主要用来维持母线电压稳定，一侧通过耦合变压器串联到线路中，主要用来控制线路潮流，合理调节系统有功和无功的流动，提高线路的传输能力。目前，UPFC控制器主要采用的是基于同步旋转dq坐标系的控制方法。并联换流器的输出电流iE被分解为iEd和iEq两个分量，通过控制d轴分量iEd用来控制直流电容两侧的电压，通过控制q轴分量iEq用来控制并联换流器接入点的母线电压；串联换流器注入系统的电流iB被分解成iBd和iBq，线路传输的有功功率P由q轴分量iBq控制，线路传输的无功功率Q有d轴分量iBd控制。采用PI调节器的控制器比较常见，而采用神经网络、模糊控制等方案虽然在理论上有较好的控制效果，但由于缺乏实践的验证，在工程应用上比较少见。若UPFC控制器间存在较强的交互影响，将影响UPFC控制器的正常运行以及系统稳定性。规范型理论(NormalForm)，是一种非常强大的数学工具，广泛用于研究电力系统的模式交互分析、系统稳定域研究及其控制器设计。因此可以利用规范型理论评估UPFC控制器间的交互影响。规范型理论描述如下：技术实现要素：发明目的：为了克服现有技术中存在的不足，本发明提供一种UPFC控制器间交互影响的规范型评估方法，依据电力系统的非线性方程，应用规范型理论，得到非线性交互指标，并进行UPFC控制器间交互影响的量化分析，可以用于定量分析UPFC控制器之间交互影响的强弱。技术方案：为实现上述目的，本发明采用的技术方案为：一种UPFC控制器间交互影响的规范型评估方法，依据系统非线性状态方程，利用规范型理论，分别计算不同工况下含UPFC控制器的系统非线性交互影响指标，比较不同工况下系统非线性交互影响指标的大小，进而判断UPFC控制器间交互影响的强弱，具体包括如下步骤：(1)收集系统中发电机与励磁系统参数、输电线路参数和UPFC参数，计算当前工况下状态变量与代数变量的稳态值，得到当前工况下含UPFC控制器的系统非线性状态方程：其中：x＝[x1x2…xi…xn]，xi是系统的第i个状态变量，是x的一阶导数；f(x)＝[f1f2…fi…fn]，fi是f(x)中的第i个方程；(2)对含有UPFC控制器的系统非线性状态方程在稳态点进行泰勒级数展开，并保留到二阶非线性项，可以得到：其中：A是系统非线性状态方程的雅克比矩阵，A中第i行第j列的元素为Hi是二阶偏导数的海森(Hessian)矩阵，Hi中第j行第k列的元素为xT是x的转置；计算A的特征值矩阵Λ＝[λ1λ2…λj…λn]，左特征向量V和右特征向量U，λj对应系统的第j个振荡模态；(3)假设存在x＝UY变换，将x＝UY带入式(2)进行若当(Jordan)变换，计算若当型系数其中：Y是若当变量，Y＝[y1y2…yj…yn]T，是yj的一阶导数；YTCjY是中的二次项，Cj是YTCjY中的系数矩阵，Cj中第k行第l列的元素为VT是V的转置，是VT中第j行第i列的元素；(4)进行规范型变换，并计算规范型系数：Y＝z+h(z)(5)其中：z是规范型变量，z＝[z1z2…zj…zn]；h(z)是以n个矩阵为元素的向量，h(z)中第j个矩阵的第k行第l列的元素为(5)通过求解非线性优化问题获得z的初始值z0：ming(z0)＝z0+h(z0)-Y0(6)其中：Y0是Y的初始值；(6)评价当前工况下，系统的第j个振荡模态下的非线性交互影响指标index(j)：其中：zk0、zl0、zj0分别为zk、zl、zj的初始值；(7)针对不同工况重复步骤(1)～(6)，得到不同工况下系统的第j个振荡模态下的非线性交互影响指标；针对UPFC上某一个控制器，所有控制器(包含该控制器)均闭环得到的非线性交互影响指标与该控制器单独闭环(其他控制器开环)得到的非线性交互影响指标差值越小，则认为该控制器与其他控制器的交互影响越弱，反之越强。有益效果：本发明提供的UPFC控制器间交互影响的规范型评估方法，可以评估UPFC各控制间交互影响的强弱，为协调设计UPFC上各控制器，改善控制器性能提供依据，进而避免令UPFC运行效果恶化的交互作用。附图说明图1为装有UPFC的四机两区域电力系统；图2为UPFC等效电路图；图3为定直流电压控制器的传递框图；图4为定交流电压控制器的传递框图；图5为定有功功率控制器的传递框图；图6为定无功功率控制器的传递框图；图7为工况4下各控制器的仿真图。具体实施方式下面结合附图对本发明作更进一步的说明。一种UPFC控制器间交互影响的规范型评估方法，依据系统非线性状态方程，利用规范型理论，分别计算不同工况下含UPFC控制器的系统非线性交互影响指标，比较不同工况下系统非线性交互影响指标的大小，进而判断UPFC控制器间交互影响的强弱，具体包括如下步骤：(1)收集系统中发电机与励磁系统参数、输电线路参数和UPFC参数，计算当前工况下状态变量与代数变量的稳态值，得到当前工况下含UPFC控制器的系统非线性状态方程：其中：x＝[x1x2…xi…xn]，xi是系统的第i个状态变量，是x的一阶导数；f(x)＝[f1f2…fi…fn]，fi是f(x)中的第i个方程；(2)对含有UPFC控制器的系统非线性状态方程在稳态点进行泰勒级数展开，并保留到二阶非线性项，可以得到：其中：A是系统非线性状态方程的雅克比矩阵，A中第i行第j列的元素为Hi是二阶偏导数的海森(Hessian)矩阵，Hi中第j行第k列的元素为xT是x的转置；计算A的特征值矩阵Λ＝[λ1λ2…λj…λn]，左特征向量V和右特征向量U，λj对应系统的第j个振荡模态；(3)假设存在x＝UY变换，将x＝UY带入式(2)进行若当(Jordan)变换，计算若当型系数其中：Y是若当变量，Y＝[y1y2…yj…yn]T，是yj的一阶导数；YTCjY是中的二次项，Cj是YTCjY中的系数矩阵，Cj中第k行第l列的元素为VT是V的转置，是VT中第j行第i列的元素；(4)进行规范型变换，并计算规范型系数：Y＝z+h(z)(5)其中：z是规范型变量，z＝[z1z2…zj…zn]；h(z)是以n个矩阵为元素的向量，h(z)中第j个矩阵的第k行第l列的元素为(5)通过求解非线性优化问题获得z的初始值z0：ming(z0)＝z0+h(z0)-Y0(6)其中：Y0是Y的初始值；(6)评价当前工况下，系统的第j个振荡模态下的非线性交互影响指标index(j)：其中：zk0、zl0、zj0分别为zk、zl、zj的初始值；(7)针对不同工况重复步骤(1)～(6)，得到不同工况下系统的第j个振荡模态下的非线性交互影响指标；针对UPFC上某一个控制器，所有控制器均闭环得到的非线性交互影响指标与该控制器单独闭环(其他控制器开环)得到的非线性交互影响指标差值越小，则认为该控制器与其他控制器的交互影响越弱，反之越强。在含有一台UPFC控制器和m台发电机的电力系统中，发电机采用三阶模型，励磁系统采用一阶模型，UPFC控制器采用9阶模型。第i台发电机的状态方程包括：式(8)中的代数变量通过式(9)求得：式中：δi为第i台发电机转子相对于同步参考轴的角位移，ωi是第i台发电机的转速，ω0为同步转速；Mi为第i台发电机的转子运动惯性常数，Di为第i台发电机的转子运动阻尼系数；Pmi和Pi分别为第i台发电机的输入机械功率和输出电磁功率；Eqi'为第i台发电机的交轴暂态电动势，Eqi为第i台发电机对应实际励磁电流的空载电动势，Efd0i为第i台发电机对应于励磁电压作用下的励磁电流强制分量的空载电动势，Efdi'为第i台发电机自动电压调节器的输出电压；Td0i'为第i台发电机的励磁绕组本身的时间常数；Vgi为第i台同步发电机的机端电压幅值，Vrefgi为第i台发电机的机端电压的给定参考值；KAi和TAi为第i台发电机的自动电压调节器的增益和时间常数，Vdi和Vqi为第i台发电机机端电压在自身di-qi旋转坐标系下的直轴和交轴分量，Idi和Iqi为第i台发电机输出电流在自身di-qi旋转坐标系下的直轴和交轴分量；Xdi、Xqi、Xdi'为第i台发电机的直轴电抗、交轴电抗和直轴暂态电抗。UPFC控制器的状态方程为：式中：Vdc为UPFC直流电容电压，Vdcref为UPFC直流电容参考电压，Cdc为UPFC直流电容；VEd和IEd为UPFC并联侧的电压和电流的d轴分量，VEq和IEq为UPFC并联侧的电压和电流的q轴分量，VBd和IBd为UPFC串联侧的电压和电流的d轴分量，VBq和IBq为UPFC串联侧的电压和电流的q轴分量；VEd'和IEd'为UPFC并联侧的电压和电流的d轴分量的计算值，VEq'和IEq'为UPFC并联侧的电压和电流的q轴分量的计算值；VBd'和IBd'为UPFC串联侧的电压和电流的d轴分量的计算值，VBq'和IBq'为UPFC串联侧的电压和电流的q轴分量的计算值；VEdref和IEdref为UPFC并联侧的参考电压和参考电流的d轴分量，VEqref和IEqref为UPFC并联侧的参考电压和参考电流的q轴分量；VBdref和IBdref为UPFC串联侧的参考电压和参考电流的d轴分量，VBqref和IBqref为UPFC串联侧的参考电压和参考电流的q轴分量；Ki1～Ki8和Kp1～Kp8分别为四个UPFC的8个PI控制器的积分系数和比例系数；XE为UPFC并联侧等效电抗，XB为UPFC串联侧等效电抗；V3d,V4d,V5d和V3q,V4q,V5q为连接UPFC的节点电压的d轴、q轴分量。因此可知系统的状态变量为：x＝[x1x2…xi…xn]＝[…,δi,ωi,Eqi',Efdi',…,Vdc,IEd',VEd',IEq',VEq',IBd',VBd',IBq',VBq']光滑矢量场为：f(x)＝[…,fi1,fi2,fi3,fi4,…,f5,f6,f7,f8,f9,f10,f11,f12,f13]，i＝1,2,…,m利用式(2)对进行泰勒级数展开，得到雅克比矩阵A为：再计算海森矩阵，以Hi2为列，Hi2为：下面以四机两区电力系统为例说明分析过程。该电力系统包含14个节点：1、2、3、4节点为发电机，节点7和节点9为负荷，其他节点为母线；其中，UPFC的串联部分安装在节点12与节点13之间，UPFC的并联部分安装在节点14上，如图1所示。四机两区域电力系统及UPFC的参数(均为标幺值)如下：表1四机两区电力系统的节点参数表2四机两区电力系统的线路参数起始节点终止节点线路电阻线路电抗线路电纳1500.016702600.0167031100.0167041000.01670560.00250.0250.04375670.0010.010.0175780.0110.110.1925780.0110.110.192581200.033081400.033013900.0770890.0110.110.19259100.0010.010.017510110.00250.0250.04375表3四机两区电力系统的发电机及励磁参数表4UPFC及其控制器参数UPFCCdc1Udc1XE0.02XB0.01控制器1Kp15Ki10.01Kp22Ki20.02控制器2Kp32Ki30.02Kp42Ki40.02控制器3Kp52Ki50.02Kp62Ki60.02控制器4Kp72Ki70.02Kp82Ki80.02对于四机两区电力系统，表5列出4种不同的工况，分别计算关键模态处的非线性交互影响指标，比较不同工况下该指标的大小，从而定量分析UPFC不同控制器间交互影响的强弱程度。表6给出了装有一台UPFC的四机两区电力系统的机电振荡模式。表5UPFC4种运行工况工况1工况2工况3工况4直流电压控制器闭环闭环闭环闭环交流电压控制器开环闭环开环闭环潮流控制器开环开环闭环闭环表6装有一台UPFC的四机两区电力系统机电振荡模式模态特征值阻尼比频率(Hz)模态类型参与机组1/3-0.139±j5.7660.0240.917局部模式G1、G22/4-0.160±j6.0750.0260.966局部模式G3、G45/6-0.160±j2.7890.0570.443区域模式G3、G4、G2、G1表7列出了四种工况下非线性交互影响指标。UPFC的正常运行需要保持直流电容上的电压恒定，以只有直流电压控制器闭环的工况1为基准，比较其他工况下的非线性交互影响指标。从表7中的数据可以发现，工况2、工况3与工况1相比，非线性交互影响指标相差不大。因此，定交流电压控制器闭环或定潮流控制器闭环与定直流电压控制器的交互影响很弱。进一步对比工况2、工况3与工况4，这三种工况下，非线性交互影响指标同样相差很小。因此，定直流电压控制器、定交流电压控制器和定潮流控制器全部闭环时，各个控制器之间的交互影响很弱。表7非线性交互影响指标模态工况1工况2工况3工况41/37.8916.1419.1117.832/41.633.541.644.105/61.252.373.029.56为了验证分析结果，在工况4下，分别对定直流电压控制器、定交流电压控制器、定有功功率控制器进行仿真测试，测试结果如图7所示。图7(a)中，定直流电压控制器的参考电压Vdcref在1s时增加1％，波形没有明显振荡，逐渐趋于平稳。图7(b)中，定交流电压控制器的参考电压Vref在1s时增加2％，仿真波形在阶跃后趋于稳定。图7(c)中，定有功功率控制器的参考值Pref在1s时增加5％，波形经过小幅振荡后趋于平稳。因此，仿真结果验证了规范型分析结果的正确性，即当UPFC所有控制器均闭环时，各控制器间交互影响很弱。以上所述仅是本发明的优选实施方式，应当指出：对于本
技术领域：
的普通技术人员来说，在不脱离本发明原理的前提下，还可以做出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。当前第1页1 2 3