一种永磁同步电机滑模变结构位置控制的方法与流程

本发明属于电动机设备领域，具体涉及永磁同步电机的一种反馈控制方法。

背景技术：

经检索，目前线性二次性型（LQ）最优控制是线性系统状态反馈控制的一种常用的方法。该方法已被应用到永磁同步电机的控制中，但是其最优性能仅适合于额定条件下。其工作原理是通过对转子磁场定向控制，建立转子旋转的坐标系，将控制信号变换成三相电流给定信号，分别与三相实际电流比较，产生电流跟踪PWM信号。然后采用二次型控制形成反馈，状态反馈控制增益也是建立在最优控制的基础上。通过寻找补偿输入，定义一个新的跟踪状态，来控制整个反馈系统。

以上二次型（LQ）控制有以下几个缺点：（1）对参数变化敏感，抗外部的干扰能力弱；（2）鲁棒性能差，动态反应较慢；（3）反馈系数过大，导致系统稳定性变差。因此，这种位置的控制方法容易受到外部因素的影响，随着这些不确定因素往往会影响系统性能，使滑模控制系统品质下降，甚至造成系统不稳定。

故近年来国内外许多学者还在致力于研究怎样解决此类问题以及研发更好的控制方法。

技术实现要素：

针对上述现有技术的缺点，本发明提出在传统控制的基础上将整个扰动P反馈给控制模块的一种永磁同步电机滑模变结构位置控制的方法。

本发明技术方案是：测试单元模块将整个扰动误差反馈给耦合器，耦合器将耦合得到的误差分别送到PI位置控制器和PI速度控制器，PI控制器以下述数学模型进行运算：

上式中，表示永磁同步电机的位置控制的增广系统函数，A和B为电机内部矩阵参数，x为三相坐标矩阵，u为补偿输入参数矩阵，θ_r为转子位置角度；

PI位置控制器和PI速度控制器的信号经3s/2s变换模块输出至PMSM矢量控制模块，PMSM矢量控制模块输出的PWM信号输出至三项逆变器模块，用于对永磁同步电机控制。

本发明采用将整个扰动误差P反馈给耦合器，然后重新通过PI控制器进行调节，PI速度控制器采用的控制模块的数学模型为：

当时，额定响应和系统控制在滑膜面上，使趋于坐标原点。

上式中A和B分别为电机内部矩阵参数，x为三相坐标矩阵，u为补偿输入参数矩阵，P为反馈参数，θ_r为转子位置角度；为滑模面位置渐近线函数，，β为扰动上边界大小, 表示上下边界参数的比值，为符号函数，函数表示的滑模面函数。

本发明的工作原理为：本发明在传统控制方法的基础上将整个误差反馈P同时间进行反馈，将整个扰动P反馈到耦合器，然后通过PI控制进行调节，计算原理方程式为：

由上式建立数学模型，数据通过PI位置控制器和PI速度控制器进行调节。然后在PMSM发生器模块采用本发明的控制算法，进行滑模函数计算，满足，=0，系统渐近稳定，实现控制与系统不确定因素基本无关。

这种控制方法有利于消除不确定边界对变结构控制造成的影响，减小外部干扰产生的误差，系统满足滑模面的方程的解趋近等于零，最后达到稳定状态。

本发明在传统控制方法的基础上添加了整个扰动反馈P，将整个扰动P反馈给耦合器，通过PI控制重新调节，将整个扰动反馈P重新进行处理。本发明的这种控制方法有利于消除不确定边界对变结构控制造成的影响，减小外部干扰产生的误差，系统满足滑模面的方程的解趋近等于零，最后达到稳定状态。本发明能降低扰动对瞬态的影响，不会对整个系统的性能带来危害。

附图说明

图1为传统的LQ变结构系统控制框图。

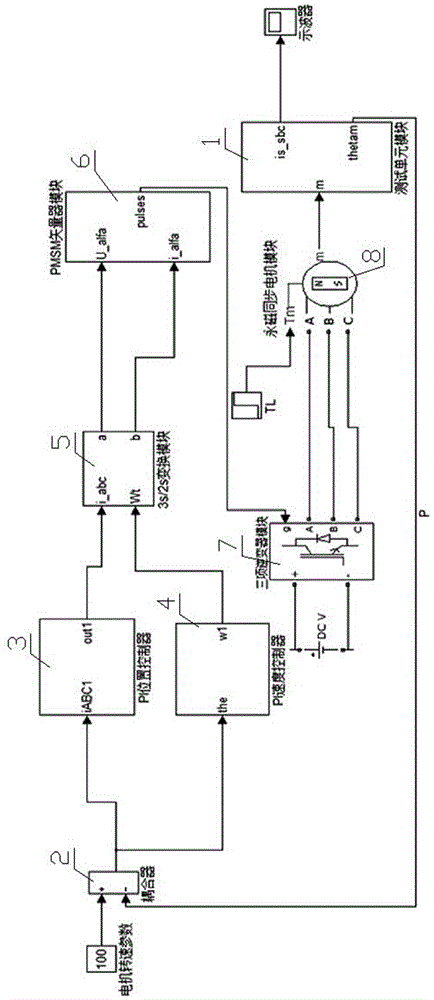
图2为本发明的控制原理图。

图3在额定条件下，本发明控制的系统的转子位置与时间的关系图。

图4在额定条件下，传统LQ控制的系统的转子位置与时间的关系图。

图5突加负载转矩时，本发明控制的系统的转子位置与时间的关系图。

图6突加负载转矩时，传统LQ控制的系统的转子位置与时间的关系图。

图7转动惯量J变化时，本发明控制的系统的转子位置与时间的关系图。

图8转动惯量J变化时，传统LQ控制的系统的转子位置与时间的关系图。

图9阻尼系数B变化时，本发明控制的系统的转子位置与时间的关系图。

图10阻尼系数B变化时，传统LQ控制的系统的转子位置与时间的关系图。

具体实施方式

一、设计滑模切换函数，使系统进入滑模运动后收敛于系统控制期望点。通过对永磁同步电机的转子建立坐标系，设d轴定子电流i_{d =0}，可以用ω_r、i_d、u_q用作状态变量建立永磁同步电机的数学模型，可表示为：

转矩方程为：

设定数学模型中的系数。

转子的位置模型为：

以上ω_r 为电机实际机械角速度，为参考转速，i_d表示d轴的定子电流，R_s为电机的阻尼电阻，为转子永磁铁磁极的励磁磁链，L_q为电机的直流电感，u_q为q轴输出电压，T_L表示电机的负载阻力矩，T_e表示永磁同步电机的电磁转矩，P_n为电机极对数，电机电磁转矩转比于i_d，K_t为系数， 为转子位置，J为电机转动惯量。

1、如图1所示，传统LQ的二次型控制方法：

LQ传统二次型的工作原理为：如果图1所示，反馈模块将反馈的位置坐标和加速度分别单独反馈到PI位置控制器模块和PI速度控制器模块，然后通过控制器按照的方法来计算反馈导致的误差，再通过控制器产生PWM信号送给电机。电机通过测试模块，再通过反馈模块进行循环反馈。这样工作导致控制不能消除外部干扰，参数反馈不能协调一致，导致系统不稳定。

以上方程式的p_T代表转矩误差。

其中，反馈模块将K1角速度误差反馈PI速度控制器中，反馈模块将K2坐标误差反馈至PI控制器模块中。

传统的二次型控制形成反馈中，其控制规律方程为：

其中，k为反馈增益矩阵，；u(t)为i_q；u_c (t)为补偿输入。

由于在伺服跟踪控制系统中，寻找补偿输入u_c (t)很困难，因此，采用一个新的跟踪控制状态：

其中为参考输入。定义变量 。

则永磁同步电机的位置控制增广系统可以表示成：

由上式可知，该系统是可控的，采用下图的控制律，在控制系统稳态时，Z为零。

控制系统的框图如图1所示，如果该系统渐近稳定，整个系统对参数变化或反馈增益变化就是鲁棒性。鲁棒性就是系统的稳定和和抗干扰的能力，这里的鲁棒性就是指系统反馈的误差的大小。

状态反馈控制增益k的选择，建立在最优控制率基础上，目标是使性能指标最小。如下：

其中，权值矩阵Q是非负定矩阵，R是正定矩阵。为了得到最优控制律，需要解决Ricatti方程：

方程的解为非负定矩阵，因此可控，使性能指标J最小。反馈增益为：

其中K表示反馈增益，u为补偿输入，A和B为电机内部参数矩阵，A^T和B^T分别为A和B矩阵的转制，R为正定矩阵，Q为权值矩阵。

此时当扰动存在时，需要一个大的反馈增益k来快速地减小误差，这样会产生一个大的电流命令，而且k中的系数太大，系统的稳定性将变差。

2、本发明的控制方法：

如图2所示，测试单元模块1将整个的扰动误差同一时间统一反馈到耦合器2，耦合器2将整个误差分别送到PI位置控制器3和速度控制器4，经PI位置控制器3和速度控制器4分别调节，PI位置控制器3对整个扰动反馈后的计算方程式如下：

PI位置控制器3和速度控制器4分别处理后的结果通过3s/2s模块5送给PMSM矢量控制模块6进行算法控制产生电机PWM信号，再将信号送给三项逆变器模块7，然后由三项逆变器7来控制电机8；电机8再通过测试单元模块1将产生误差继续反馈，形成误差反馈的循环，不断减小电机系统产生的误差。这样将整个扰动P反馈同一时间反馈到PI控制器，有利于消除外部干扰，增强系统鲁棒性。

本发明计算方案如下：

（1）首先，设计扰动反馈后PI控制数学模型。

建立LQ-VSC数学模型：

其中，分别表示系统的矩阵输入参数，A和B表示x和t的矩阵参数，ΔA和ΔB表示系统不确定的参数变化，d表示外部扰动，θ_r表示角速度和转子误差参考输入量，u表示补偿输入。

上式变换写成：

上式中，P为整个扰动，公式如下：

Δa和Δb分别为反馈矩阵参数变化量。

（2）然后，采用如下式的控制算法，保证额定响应和系统控制能在滑模面上。

方程式如下：

其中表示滑模面函数，sgn(S)为符号函数，β为扰动上边界大小。

计算渐近稳定的表达式：

上式中，为滑模面位置函数，其中，p_n为极对数，J为转动惯量。

推导结果满足：

其中上式为滑模面位置函数，，k1，k2，k3为电机内部参数，x₁，x₂，x₃三相坐标位置，β为扰动上边界大小，表示上下边界参数的比值，为符号函数，函数表示的滑模面函数。

当上式成立时，才有=0，系统才能渐近稳定。

总结：如图2所示，本发明在传统控制方法的基础上添加了整个扰动反馈P，通过将整个的扰动误差同时间统一反馈到前面耦合器，耦合得到的误差送到PI控制器里。

然后把整个扰动误差计算到以下数学模型当中：

再通过3s/2s模块，送给PMSM矢量控制模块进行算法控制产生电机PWM信号，由PMSM矢量控制模块进行滑模函数计算。

对渐近线进行计算

通过计算上式解满足，=0，系统渐近稳定，实现控制与系统不确定因素基本无关。

本发明的这种控制方法有利于消除不确定边界对变结构控制造成的影响，减小外部干扰产生的误差，系统满足滑模面的方程的解趋近等于零，最后达到稳定状态。本发明能降低扰动对瞬态的影响，不会对整个系统的性能带来危害。

本发明以上方案的实施例：

首先定义开关函数为：

其中，x₀是x的初始值，C为常矢量，；要求。

由于传统最优控制是在电机额定参数下设计的，当这些参数发生变化或存在扰动时，最优指标不能满足要求，系统性能恶化，稳态误差增加。因此，本发明的控制数学模型也可以写成：

其中，p表示整个扰动，p为标量函数，公式为：

其系统控制的框图如图2所示。

二、设计滑模控制算法，形成滑动模态运动。

为了保证额定响应和系统控制能在滑模面上，本发明控制的算法为：

计算渐近稳定的表达式：

计算得满足条件：

根据滑模变结构控制存在的条件，上式结果满足滑模面存在的条件，则系统必定渐近稳定，且x(t)将滑向原点。

三、进行程序模拟仿真：

仿真所选择的权值矩阵Q和R分别为：

这是最优增益矩阵：

此时，设定系统的极点分别为-4.5，-30.6+j30.6，-30.6-j30.6。控制的目的是驱动电机旋转到给定位置，用传统的LQ与本发明的LQ-VSC进行模拟仿真。

模拟的程序原理图如图2所示。

四、通过simulink仿真软件进行系统控制方法模拟仿真，对比本发明方法与传统LQ控制方法的性能差异：

通过对驱动电机旋转到给定的位子，用传统的LQ控制和LQ-VSC控制分别对系统进行仿真实验得到图3至图10的仿真曲线图，通过仿真曲线图可以得到以下结论：

（1）在额定条件下LQ控制的系统受到扰动的影响很大，而LQ-VSC控制下系统受扰动的影响很小，如图3和图4所示；（2）在突加负载转矩时系统的位置响应，LQ出现较大波动，而LQ-VSC基本稳定，如图5和图6所示；（3）在转动惯量J变化时LQ控制出现下降然后回到平衡，而LQ-VSC控制的转动惯量J基本保持稳定值不变，如图7和图8所示；（4）当阻尼系数B变化时，LQ控制的阻尼系数值出现上下波动变化，而LQ-VSC保持稳定不变，如图9和图10所示。

因此，本发明对于永磁同步电机滑膜变结构位置控制LQ-VSC与LQ反馈控制相比，消除了不确定边界对变结构控制造成的影响，外部干扰产生的误差明显变小，最终系统趋近稳定状态，达到了预期的效果。