一种新能源柔性直流并网可靠性估计方法与流程

本发明属于电网规划领域，涉及一种新能源柔性直流并网可靠性估计方法。
背景技术：
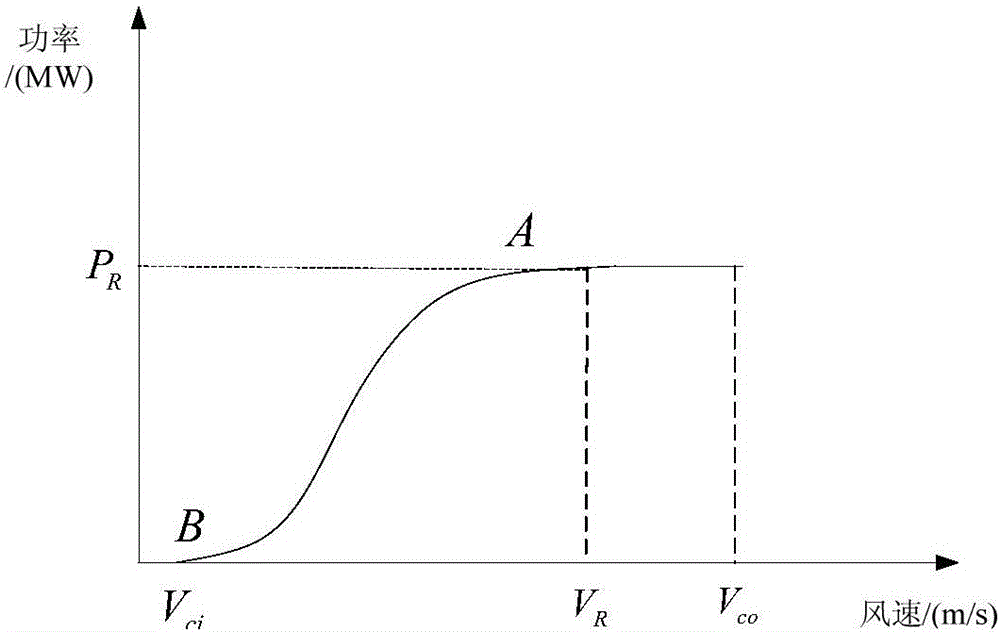
：随着经济发展，能源和环境问题日益突出，发展可再生能源成为各国实施可持续发展的重要选择。目前，风能、太阳能等新能源开发已进入大规模商业化阶段，尤其是风能的开发，传统的风电场并网方式以交流加静止无功补偿器(SVC)的方式接入公用电网，但随着风能开发规模的加大，柔性直流并网成为风能并网的发展趋势，如图1，风能发电具有典型的波动性与间歇性特点，传统的可靠性评估指标与方法已难以满足风能并网系统的精准评估需求。技术实现要素：本发明的目的在于克服上述现有技术的缺点，提供了一种新能源柔性直流并网可靠性估计方法，该方法能够准确估计得到风电场并网后直流输电网络的可靠性。为达到上述目的，本发明所述的新能源柔性直流并网可靠性估计方法包括以下步骤：1)确定风电场的装机容量，给定风电场机组的故障率，再进行风速抽样，然后根据风速抽样的结果及风电场的装机容量构建风电场机组的出力模型，并根据风电场机组的出力模型及风电场机组的故障率计算风电场的机组出力，并将所述风电场的机组出力作为风电场机组的发电量；2)统计模拟时间内风电场机组的总出力，确定风电场机组的平均出力期望，然后计算风电场机组的平均出力期望与风电场机组的装机容量之比，并将计算的结果作为风电场容量因子C；3)根据MMC-HVDC换流器原理基于马尔科夫过程与FD理论构建MMC换流器子系统的可靠性等效模型，同时构建直流输电网络中输电线路的可靠性模型；4)采用串并联网络法将直流输电网络中各MMC换流器子系统的可靠性等效模型与输电线路的可靠性模型进行组合，计算组合后直流输电网络的故障率、平均故障时间及等效故障率，然后根据组合后直流输电网络的故障率、平均故障时间及等效故障率计算组合后直流输电网络的不可用率U；5)计算风电场的功率送出概率Pout、组合后直流输电网络的故障受阻电量ESF及组合后直流输电网络的等效强迫不可用率EUEQ，然后根据风电场的功率送出概率Pout、组合后直流输电网络的故障受阻电量ESF、组合后直流输电网络的等效强迫不可用率EUEQ以及组合后直流输电网络的不可用率U估计风电场接入直流输电网络后直流输电网络的可靠性。风电场容量因子C的表达式为：C=ETAT×SN---(6)]]>其中，T为统计模拟时间，ETA为统计模拟时间内风电场机组的实际发电量，SN为风电场额定容量。风电场的功率送出概率Pout的表达式为：其中，SN为风电场额定容量。组合后直流输电网络的故障受阻电量ESF的表达式为：ESF＝8760(C×SN-SEQ)(8)组合后直流输电网络的等效强迫不可用率EUEQ的表达式为：风速抽样的结果为：v＝c[lnX]1/k(4)其中，v为风速，X为均匀分布随机变量，k为威布尔分布形状参数，c为风电场的尺度参数。风电场机组的出力模型为：Pi=0,0≤vi<VciPRvi-VciVR-Vci,Vci≤vi<VRPR,VR≤vi<Vco0,vi>Vco---(5)]]>其中，Pi为风电场机组的功率，PR为风电场机组的输出功率额定值，Vci为风电场机组要求的最小风速，VR为风电场机组的额定风速，Vco为风电场机组的切出风速。本发明具有以下有益效果：本发明所述的新能源柔性直流并网可靠性估计方法在具体操作时，采用串联网络法将风电场接入到直流输电网中，构建直流输电网络中各MMC换流器子系统的可靠性等效模型，再采用串并联网络法将各MMC换流器子系统的可靠性模型进行组合，计算出组合后直流输电网络的不可用率U、故障受阻电量ESF及等效强迫不可用率EUEQ、以及风电场的功率输出概率Pout，再根据风电场的功率送出概率Pout、组合后直流输电网络的故障受阻电量ESF、组合后直流输电网络的等效强迫不可用率EUEQ以及组合后直流输电网络的不可用率U估计风电场接入直流输电网络后直流输电网络的可靠性，实现对风电场的功率送出概率Pout、组合后直流输电网络的故障受阻电量ESF及组合后直流输电网络的等效强迫不可用率EUEQ重新定义，提高估计的精准度。附图说明图1为接入风电场后直流输电网络的结构原理图；图2为风电机组输出功率曲线；图3为本发明中的桥臂状态空间图。具体实施方式下面结合附图对本发明做进一步详细描述：参考图1，本发明所述的新能源柔性直流并网可靠性估计方法包括以下步骤：1)确定风电场的装机容量，给定风电场机组的故障率，再进行风速抽样，然后根据风速抽样的结果及风电场的装机容量构建风电场机组的出力模型，并根据风电场机组的出力模型及风电场机组的故障率计算风电场的机组出力，并将所述风电场的机组出力作为风电场机组的发电量；2)统计模拟时间内风电场机组的总出力，确定风电场机组的平均出力期望，然后计算风电场机组的平均出力期望与风电场机组的装机容量之比，并将计算的结果作为风电场容量因子C；3)根据MMC-HVDC换流器原理基于马尔科夫过程与FD理论构建MMC换流器子系统的可靠性等效模型，同时构建直流输电网络中输电线路的可靠性模型；4)采用串并联网络法将直流输电网络中各MMC换流器子系统的可靠性等效模型与输电线路的可靠性模型进行组合，计算组合后直流输电网络的故障率、平均故障时间及等效故障率，然后根据组合后直流输电网络的故障率、平均故障时间及等效故障率计算组合后直流输电网络的不可用率U；5)计算风电场的功率送出概率Pout、组合后直流输电网络的故障受阻电量ESF及组合后直流输电网络的等效强迫不可用率EUEQ，然后根据风电场的功率送出概率Pout、组合后直流输电网络的故障受阻电量ESF、组合后直流输电网络的等效强迫不可用率EUEQ以及组合后直流输电网络的不可用率U估计风电场接入直流输电网络后直流输电网络的可靠性。风电场机组的出力取决于风速，首先建立风电场风速模型，目前，风电场风速建模的方法很多，主要有两参数威布尔分布模型，瑞利分布模型及时间序列模型。本文选用威布尔分布模型进行风速模拟，具体过程如下：威布尔分布函数为F(v)＝P(V≤v)＝1-exp[-(v/c)k](1)其中，k为威布尔分布形状参数，c为风电场的尺度参数。采用反函变换法产生服从威布尔分布的随机变量，反变换法的基本原理是：对于服从[0,1]上均匀分布的随机变量U，则随机变量X＝F-1(U)为一个连续累积概率分布函数F(X)。根据反函变换法，令x＝F(v)＝1-exp[-(v/c)k](2)则有，v＝c[-ln(1-x)]1/k(3)其中，x及1-x同为均匀随机变量，用1-x替代x，则上式变为v＝c[lnX]1/k(4)其中，X为均匀分布随机变量。风电机组的输出功率受风速变化影响，其关系曲线被称为风电机组功率特性曲线，图2为一典型的风电机组功率特性曲线，当风速低于切入风速Vci时，机组出力为0MW；当大于Vci时风机开始启动，在Vci与额定风速VR之间时，其关系为非线性正相关；当风速继续增大，在VR与切出风速Vco之间时，风机输出功率为额定值PR；当风速进一步增大，超过Vco时，为了风机安全，风机将自动退出运行。由于AB段曲线近似为直线，因此风电场机组的出力模型为：Pi=0,0≤vi<VciPRvi-VciVR-Vci,Vci≤vi<VRPR,VR≤vi<Vco0,vi>Vco---(5)]]>建立新能源接入系统可靠性评估指标体系1)仅受输电系统本身设备停运影响，能够反应HVDC输电系统最大输送能力的基本可靠性指标。1.HVDC输电系统年平均故障频率ff反映了HVDC输电系统每年的平均故障次数。2.HVDC输电系统各运行状态概率PiHVDC输电系统可能有不同的运行状态，如双极LCC-HVDC(单12脉)输电系统存在100％容量运行、50％容量运行和0％容量运行三种运行状态，因此用Pi分别表示各运行状态概率如下：P1为100％容量运行概率；P0.5为50％容量运行概率；P0为0％容量运行概率。3.HVDC输电系统平均故障持续时间Da(h/a-1)4.系统总等值停运时间TEOT(h/year)TEOT=f0Df0+12f0.5Df0.5=8760(P0+12P0.5)]]>其中，Df0.5为50％容量运行平均持续时间；Df0为0％容量运行平均持续时间，f0.5为单极故障频率；f0为双极故障频率。2)计算风电场出力特性，反应HVDC输电系统对风电场并网可靠性实际影响的风电HVDC并网系统可靠性指标。1.效容量SEQ(MW)效容量SEQ(MW)是将整个风电场与输电系统联合视为接入交流主网的一台等效大容量发电机，考察其T小时(一般认为T足够大)内的平均等效出力，效容量SEQ为：其中，t为时间/(小时)，p(t)为第t小时的并网功率。风电场的功率送出概率Pout的表达式为：其中，SN为风电场额定容量。风电场容量因子C的表达式为：C=ETAT×SN---(6)]]>其中，T为统计模拟时间，ETA为统计模拟时间内风电场机组的实际发电量，SN为风电场额定容量。3.系统故障受阻电量ESF(MWh/a-1)系统故障受阻电量ESF在输电系统降容量运行时，考虑了风电场出力情况，计算结果为输电系统故障引起的实际受阻电量，同时，ESF可用来计算电量损失费用，是经济性评估中的重要参考指标。ESF＝8760(C×SN-SEQ)(8)4.系统等效强迫不可用率EUEQ风电具有间歇性，传统的输电系统强迫不可用率指标，在输电系统降额运行时并未考虑电源间歇性引起的实际减小容量，不能真实反映输电系统故障对间歇性电能传输的阻碍能力。本发明考虑到风电场并网的受阻电量完全是由于输电系统强迫停运导致，因此，在此以实际受阻电量与风电场发出电量的比值来等效输电系统的强迫不可用率，系统等效强迫不可用率EUEQ能真实反映风电场输电系统对电能的可靠传输能力。(2)基于“k/n”冗余备用的MMC可靠性建模及子模块备用优化MMC换流器基于模块化和“k/n”冗余备用设计，备用元件有冷热备用两种情况；冗余子模块的热备用优点是，冗余子模块已接入桥臂，可以立即进入运行；冷备用状态下的子模块进入运行前需将旁路开关可靠关掉，要短暂数十毫秒时间，可以忽略不计，且在每次子模块故障，热备用投入运行后，冷备用会直接自动切换到热备用状态。由于每个桥臂的冗余配置是独立的，因此首先求取每个桥臂等效可靠性模型，然后基于串联卷积公式对各桥臂进行组合，得MMC换流器子系统的可靠性等效模型。对于MMC拓扑，当应用于高压场合时，一个桥臂上串联的子模块数往往达到几十甚至上百个，并且其大小决定着MMC可以输出电平数的大小，在此以直流电压为±200kV的MMC-HVDC为例，设单个子模块SM的电压为10kV，MMC每个桥臂的子模块数nSM由直流电压Udc和单个子模块电压Uc共同决定，即nSM＝Udc/Uc考虑冗余配置，以20/23拓扑结构的MMC为例，建模如下：1)桥臂状态空间图如图3所示，只有子模块在无备用的情况下故障，才会导致桥臂故障，因此，只有状态4为故障状态。则状态转移矩阵T为：T=1-21λ21λ000μ1-μ-21λ21λ0002μ1-2μ-21λ21λ0003μ1-3μ-20λ20λ0004μ1-4μ]]>2)采用状态空间法，得MMC桥臂各状态概率Pi为：Σi=1nPi=1]]>PT＝P3)MMC桥臂正常状态集合由状态1、2、3、4组成，故障状态集合由状态5单独构成，由所求各状态概率累加得两状态集合概率；4)根据FD理论，得两状态集合的转移频率为：fs＝P4*4μ5)由图3知MMC单个桥臂等效两状态可靠性模型的修复率为4μ，则平均修复时间为1/4μ；然后将正常状态集合概率和状态集合转移频率fs代入公式Pi＝fidi得桥臂平均无故障工作时间，进而得等效故障率；6)MMC各桥臂间存在串联关系，任一桥臂故障都将导致MMC换流器故障，对桥臂等效两状态模型进行串联卷积，求得MMC等效故障率和修复时间，进而得等效修复率。当前第1页1 2 3