一种基于电容电荷平衡升降压DC‑DC开关电源系统及控制方法与流程
本发明属于电子设计技术领域,具体涉及一种基于电容电荷平衡升降压DC-DC变换器系统及控制方法。
背景技术:
实际应用中,很多设备需要电源,开关电源因功耗小、效率高等特点渐渐地被应用在各个领域。开关电源分为AC-DC和DC-DC两大类,控制方法的选择和设计对其性能十分重要,采用不同的检测信号和控制电路会有不同的控制效果。
现有的基于伏秒平衡原理控制的DC-DC变换器和滞环电流控制的DC-DC变换器,输出负载电流变化时,暂态过程电路处于断续导电模式(CCM)均具有较好的动态性能。但负载电流突变范围较大电路进入断续导电模式(DCM)时,动态性能将不是很理想,影响供电设备的稳定性、可靠性,限制其应用场合。因此,设计一种基于电容电荷平衡升降压DC-DC变换器系统及控制方法具有应用价值。
技术实现要素:
为了克服上述现有技术的不足,本发明的目的是提供一种基于电容电荷平衡升降压DC-DC变换器系统及控制方法,利用电容电荷平衡原理,根据变换器不同的工作模式提出对应的暂态滞环电流控制策略,在DCM下,使得变换器仍具有较好的动态性能,满足实际需求。
为了实现上述目的,本发明采用的技术方案是:
一种基于电容电荷平衡升降压DC-DC变换器系统,包括DC-DC变换器、采样电路、判断处理电路和控制电路,DC-DC变换器输出端连接采样电路的输入端,采样电路输出端连接判断处理电路的输入端,判断处理电路的输出端连接控制电路的输入端,控制电路的输出端连接DC-DC变换器形成闭环反馈系统;
所述的DC-DC变换器采用BUCK-BOOST DC-DC变换器拓扑结构,实现宽范围电压输入;
所述的采样电路采样输出电流、电感电流和输出电压和输入电压,并将采样信息发送到判断处理模块;
所述的判断处理电路采用处理器STM32F4,实现判断输出负载电流是否发生突降,如果突降,判断电路工作模式,连续导电模式(CCM)或断续导电模式(DCM),并发送信息到控制电路模块;
所述的控制电路输出频率占空比可变的PWM波,精确地控制BUCK-BOOST DC-DC变换器开关管的导通与关断。
一种基于电容电荷平衡的升降压DC-DC变换器系统及控制方法,包括以下步骤:
1)采样电路采样输出电流、电感电流、输出电压和输入电压;
2)将采样信息送入判断处理模块,根据BUCK-BOOST DC-DC变换器输入输出电压之间的关系,推导出实时平均电感电流IL(t);
3)处理器将前一时刻的IL2和这一时刻IL1作比较,判断负载电流是否发生变化,如果IL2-IL1>ΔI,则突变发生,反之,负载电流保持不变;如果突降,判断电路工作状态是DCM还是CCM;
4)根据判断结果采用相应的控制策略,如果负载电流变换范围较大进入DCM,则采用DCM控制策略,如果变化范围较小处于CCM,则采用CCM控制策略。
5)根据不同步控制策略,控制变换器开关管的占空比,使输出电压稳定。
所述的步骤1)中电流检测电路采用霍尔传感器CSM001A,其匝数比为25:1000,可根据电路电流大小i和处理器处理最大电压Vmax,计算出采样电阻R,即满足R<Vmax/(40i)。
所述的步骤3)中判断突变后电路工作模式是DCM或CCM,具体步骤为:
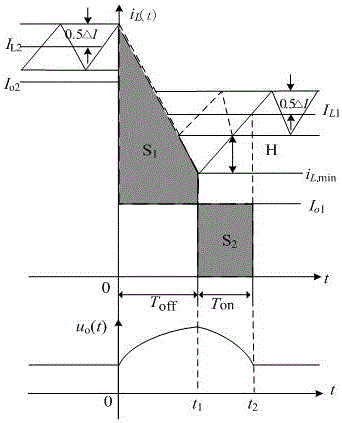
1)负载电流突变,假定变换器处于CCM,根据电容电荷平衡原理,分析出理想的波形如图2所示。图中Io2和Io1分别为前一时刻IL2和这一时刻IL1对应的输出平均电流,H为变换器暂态参数;
2)负载电流突降,开关关断,电容C充电电荷量为Q1,即S1的面积,如式(1),
iL1,min为电感电流最小值,其中如式(2)
3)电感电流最小时,开关导通,电容C放电电荷量为Q2,即S2的面积,则如式(3)、式(4),
Q2=Io1×Ton (3)
其中
4)根据电容电荷平衡原理Q1=Q2,得式(5)
5)如果处理器计算出H>0,则电路工作于CCM,否则,电路进入DCM。
所述的步骤4)中控制策略包含CCM和DCM两部分,分析方法如下:
第一部分:CCM下,根据式(2)、(4)和(5)可求出开关管的导通与关断时间,从而精确地控制开关动作;
第二部分:DCM下,给出图3的电路波形图,电路工作过程如下:
1)负载电流突降,S关断(即0时刻)。
2)输出电压大于额定输出电压时,S保持关断(即0~t3时刻),变换器工作在以下三个阶段;
①t∈[0,t1):iL(t)>Io1,储存在电感中的能量同时给电容和负载供能,过渡过程满足微分方程为式(6),
初始条件为式(7)、式(8),
uo(0)=Ue=24 (7)
根根据式(7)和式(8),求出微分方程的解uo(t)。0到t1时刻的时间Δt1为式(9),
Δt1=(IL2+0.5ΔI-Io1)L/Ue (9)
将t1=Δt1代入uo(t),求出输出电压uo(t1);
②t∈[t1,t2):iL(t)<Io1,电容C和电感同时给负载供能,过渡过程满足微分方程为式(10),
初始条件为式(11),
根据式(11),求出输出电压uo(t),t1到t2的时间Δt2为式(12),
Δt2=Io1L/Ue (12)
将t2=t1+Δt2代入uo(t),求出输出电压uo(t2);
③t∈[t2,t3):iL=0,电路工作在DCM,仅由电容C给负载供能,过渡过程的微分方程为式(13),
将uo(t3)=24V代入式(13),求出t2到t3时刻经历的时间Δt3为式(14),
3)输出电压小于等于额定输出电压时,S导通(即t3~t4时刻),电容给负载供能,变换器满足的微分方程为式(15),
t=t4时,电感电流为iL(t4)=IL1-0.5ΔI,暂态过程结束,电路进入稳态过程,t3到t4的时间Δt4为式(16),
Δt4=(IL1-0.5ΔI)L/ui (16)
将t=Δt4代入式(16),求出输出电压uo(t4);
4)根据每阶段工作时间,可精确地控制开关动作,实现智能控制。
本发明的有益效果是:
本发明所提供DC-DC变换器系统及控制方法可智能地判断负载电流是否变降,进而判断电路所处的工作模式是DCM或CCM,根据不同的工作模式,利用电容电荷平衡原理采取对应的控制策略,从而保证了变换器在不同的工作模式均具有较好的动态性能,提高供电设备的可靠性。
附图说明
图1为本发明的组成结构示意图。
图2为本发明CCM下变换器的理想波形图。
图3为本发明DCM下变换器的理想波形图。
图4为本发明CCM下变换器的仿真波形图。
图5为本发明DCM下变换器的仿真波形图。
其中,1为DC-DC变换器;2为采样电路;3为判断处理电路;4为控制电路模块。
具体实施方式
以下结合附图对本发明进一步叙述。
如图1所示,一种基于电容电荷平衡升降压DC-DC变换器系统,包括DC-DC变换器1、采样电路2、判断处理电路3和控制电路4,DC-DC变换器1输出端连接采样电路2的输入端,采样电路2输出端连接判断处理电路3的输入端,判断处理电路3的输出端连接控制电路4的输入端,控制电路4的输出端连接DC-DC变换器1形成闭环反馈系统;
所述的DC-DC变换器1采用BUCK-BOOST DC-DC变换器拓扑结构,实现宽范围电压输入;
所述的采样电路2采样输出电流、电感电流和输出电压和输入电压,并将采样信息发送到判断处理模块;
所述的判断处理电路3采用处理器STM32F4,实现判断输出负载电流是否发生突降,如果突降,判断电路工作模式,连续导电模式(CCM)或断续导电模式(DCM),并发送信息到控制电路模块;
所述的控制电路4输出频率占空比可变的PWM波,精确地控制BUCK-BOOST DC-DC变换器开关管的导通与关断。
一种基于电容电荷平衡的升降压DC-DC变换器系统及控制方法,包括以下步骤:
1)采样电路采样输出电流、电感电流、输出电压和输入电压;
2)将采样信息送入判断处理模块,根据BUCK-BOOST DC-DC变换器输入输出电压之间的关系,推导出实时平均电感电流IL(t);
3)处理器将前一时刻的IL2和这一时刻IL1作比较,判断负载电流是否发生变化,如果IL2-IL1>ΔI,则突变发生,反之,负载电流保持不变;如果突降,判断电路工作状态是DCM还是CCM;
4)根据判断结果采用相应的控制策略,如果负载电流变换范围较大进入DCM,则采用DCM控制策略,如果变化范围较小处于CCM,则采用CCM控制策略。
5)根据不同步控制策略,控制变换器开关管的占空比,使输出电压稳定。
所述的步骤1)中电流检测电路采用霍尔传感器CSM001A,其匝数比为25:1000,可根据电路电流大小i和处理器处理最大电压Vmax,计算出采样电阻R,即满足R<Vmax/(40i)。
所述的步骤3)中判断突变后电路工作模式是DCM或CCM,具体步骤为:
1)负载电流突变,假定变换器处于CCM,根据电容电荷平衡原理,分析出理想的波形如图2所示。图中Io2和Io1分别为前一时刻IL2和这一时刻IL1对应的输出平均电流,H为变换器暂态参数;
2)负载电流突降,开关关断,电容C充电电荷量为Q1,即S1的面积,如式(1),
iL1,min为电感电流最小值,其中如式(2)
3)电感电流最小时,开关导通,电容C放电电荷量为Q2,即S2的面积,则如式(3)、式(4),
Q2=Io1×Ton (3)
其中
4)根据电容电荷平衡原理Q1=Q2,得式(5)
5)如果处理器计算出H>0,则电路工作于CCM,否则,电路进入DCM。
所述的步骤4)中控制策略包含CCM和DCM两部分,分析方法如下:
第一部分:CCM下,根据式(2)、(4)和(5)可求出开关管的导通与关断时间,从而精确地控制开关动作;
第二部分:DCM下,给出图3的电路波形图,电路工作过程如下:
1)负载电流突降,S关断(即0时刻)。
2)输出电压大于额定输出电压时,S保持关断(即0~t3时刻),变换器工作在以下三个阶段;
④t∈[0,t1):iL(t)>Io1,储存在电感中的能量同时给电容和负载供能,过渡过程满足微分方程为式(6),
初始条件为式(7)、式(8),
uo(0)=Ue=24 (7)
根根据式(7)和式(8),求出微分方程的解uo(t)。0到t1时刻的时间Δt1为式(9),
Δt1=(IL2+0.5ΔI-Io1)L/Ue (9)
将t1=Δt1代入uo(t),求出输出电压uo(t1);
⑤t∈[t1,t2):iL(t)<Io1,电容C和电感同时给负载供能,过渡过程满足微分方程为式(10),
初始条件为式(11),
根据式(11),求出输出电压uo(t),t1到t2的时间Δt2为式(12),
Δt2=Io1L/Ue (12)
将t2=t1+Δt2代入uo(t),求出输出电压uo(t2);
⑥t∈[t2,t3):iL=0,电路工作在DCM,仅由电容C给负载供能,过渡过程的微分方程为式(13),
将uo(t3)=24V代入式(13),求出t2到t3时刻经历的时间Δt3为式(14),
3)输出电压小于等于额定输出电压时,S导通(即t3~t4时刻),电容给负载供能,变换器满足的微分方程为式(15),
t=t4时,电感电流为iL(t4)=IL1-0.5ΔI,暂态过程结束,电路进入稳态过程,t3到t4的时间Δt4为式(16),
Δt4=(IL1-0.5ΔI)L/ui (16)
将t=Δt4代入式(16),求出输出电压uo(t4);
4)根据每阶段工作时间,可精确地控制开关动作,实现智能控制。
上述内容均是对升降压DC-DC开关电源系统的理论分析,出于论证的严密性,在MATLAB/simulik软件中对负载电流突降过程进行了仿真验证。仿真参数为:输入电压范围为16~32V,额定输出电压为24V,开关频率f=50kHz,L=1mH,C=300μF,ΔI=100mA,负载电流突降范围分别为500mA到400mA和500mA到100mA。
从图4和图5仿真结果可以看出,负载电流突变范围不同时,电路工作于不同的模式。突变范围小,电路工作于CCM,突变范围大,电路进入DCM,针对不同的工作模式采用对应的控制策略,使得变换器均具有较好的动态性能。
- 还没有人留言评论。精彩留言会获得点赞!