一种基于改进次梯度粒子群的微电网并网优化调度方法与流程

本发明提供一种基于改进次梯度粒子群的微电网并网优化调度方法，涉及微电网并网优化调度领域。

背景技术：

随着智能电网概念的引入和推广应用，微电网将成为智能电网的重要组成部分，然而构成微电网中的分布式电源——风电和光伏发电单元，其出力特性具有较强的波动性和随机性，对微电网的实时调度会带来较强的负面影响。微电网并网优化调度问题实际上是一个高维、非线性、非凸、不可导的数学优化问题。由于存在配电网输送能力限制和系统功率平衡条件的约束，其对应的优化问题常常具有非连续、不可微等特点。现有智能优化算法中的标准PSO算法在解决这类高维度、非光滑的复杂问题时，时常会遇到早熟和收敛的问题，也就是说种群在没有找到全局最优时，已经聚集到某局部最优点而停滞不动。另一方面，标准PSO算法在接近或进入最优点区域时的收敛速度也比较缓慢，特别是后期的寻优结果不够理想，这主要是由于粒子收敛到局部极小，缺乏有效的方法使粒子远离局部极小点。

技术实现要素：

为了克服现有技术存在的不足，本发明提供一种基于改进次梯度粒子群的微电网并网优化调度方法，在解决含储能装置的微电网并网优化时，具有寻优效果好、收敛速度快的优点。

本发明所采用的技术方案是：

一种基于改进次梯度粒子群的微电网并网优化调度方法，包括以下步骤：

步骤1：含储能装置的微电网并网模型的建立：根据实际情况，以微电网总的发电成本和环境污染治理成本最小，建立优化调度目标函数；

步骤2：确立微电网系统中的运行约束条件：分别确立系统功率平衡约束、蓄电池充放电功率约束条件、微电源的输出功率限制、微电网与大电网交互的购售电约束；

步骤3：对标准粒子群算法进行改进：分别对惯性权重、加速因子进行改进，提出利用次梯度优化方法来更新粒子群算法中粒子的速度。

一种基于改进次梯度粒子群的微电网并网优化调度方法，包括以下步骤：

步骤1：含储能装置的微电网并网模型建立：根据实际情况，以微电网总的发电成本和环境污染治理成本最小，建立优化调度目标函数：

上式中，微电源的燃料成本为微电源运行维护费用为与电网交互成本为N为微电源个数；c_i为第i个微电源的燃料费用单价；m_i为第i个微电源的运维费用；p_i为第i个微电源的发电量；n为调度周期；c_b,i为i时段向大电网购电价格；c_p,i为i时段向大电网售电价格；p_b,i为i时段向大电网的购电电能(kW·h)；p_p,i为i时段向大电网的售电电能(kW·h)；；M为排放气体种类数(NO_X,SO₂,CO₂)；ω_i,j为第i个微电源产生的第j种排放气体污染物系数；α_j为第j种污染气体单位排放量的治理费用。

步骤2：确立微电网系统中的运行约束条件，如下：

(1)系统功率平衡约束：

P_load＝P_pv+P_wind+P_MT+P_grid+P_BA

式中：P_load为微电网中负荷所需的总功率；P_pv、P_wind分别为微电网中光伏和风力的输出功率；P_MT、P_grid、P_BA分别为系统对微型燃气轮机、电网和蓄电池的优化功率。

(2)蓄电池充放电功率约束条件：

式中：P_c,i为蓄电池在第i时段的充电功率；P_c,max、P_c,min为蓄电池充电功率的最大、最小值；P_f,i为蓄电池在第i时段的放电功率；P_f，max、P_f，min为蓄电池放电功率的最大、最小值。

(3)微电源的输出功率限制：

式中：P_MT为微型燃气轮机的实际输出功率；分别为微型燃气轮机输出功率的上、下限。

(4)微电网与大电网交互的购售电约束：

式中：P_b、P_s分别为微电网向大电网购、售电量；P_b,max、P_b,min分别为购电的上下限；P_s,max、P_s,min分别为售电的上下限。

步骤3：对标准粒子群算法进行改进：

步骤3.1：标准粒子群算法：

速度更新公式如下：

v_i,j(k+1)＝ωv_i,j(k)+c₁r₁[p_i,j-x_i,j(k)]+c₂r₂[p_g,j-x_i,j(k)]

位置更新公式如下：

x_i,j(k+1)＝x_i,j(k)+v_i,j(k+1)

式中：j＝1,2,…,n；ω为惯性权重；r₁,r₂为[0，1]范围内的均匀随机数；c₁,c₂为非负常数，称为学习因子。

步骤3.2：对标准粒子群算法的改进：

(1)惯性权重的改进：

惯性权重ω体现的是粒子当前速度继承先前速度的主要程度。一个较大的惯性权重有利于全局搜索，而一个较小的惯性权重则更利于局部的搜索。为了更好的平衡全局搜索与局部搜索，本发明采用线性递减惯性权重：

ω(k)＝ω_star-(ω_star-ω_end)×k/T_max

式中：ω_star为初始惯性权重；ω_end为最大迭代次数时的惯性权重；k为当前迭代次数；T_max为最大迭代次数。

(2)加速因子的改进：

参数c₁决定粒子个体历史对运动轨迹的影响，c₂决定种群的全局经验对运动轨迹的影响。在标准PSO中，c₁、c₂的取值一般为固定值。本发明采用时变加速因子：

c₁＝(c_1f-c_1e)×cos(kπ/T_max)+c_1e

c₂＝(c_2f-c_2e)×cos(kπ/T_max)+c_2e

式中：c_1e,c_1f,c_2e,c_2f分别表示c₁,c₂在优化过程开始和结束的取值。其中k为当前迭代次数，T_max为最大迭代次数。由c₁＝c₂，可得因此，当时，c₁>c₂，此时是让粒子尽量多的向最优pbest学习，使粒子的全局搜索能力增强；当时，c₁<c₂，此时使粒子向社会最优位置gbest的局部靠拢，使得局部搜索得到增强。

(3)基于次梯度的PSO算法：

基于次梯度的粒子群算法其主要思想是通过沿次梯度的反方向(负次梯度方向)搜索以找到目标函数的极小值。

x_k+1＝x_k-η_k·g_k

上式中，g_k是x_k上的一个次梯度，η_k为步长函数。由于负梯度的方向不一定是函数的下降方向。因此，通过如下的最小化函数加以保证：

其中是第k步迭代时的最佳函数值。

通过对传统粒子群算法的的速度更新公式进行修正，可以得到如下基于次梯度粒子群的更新方案：

基于次梯度粒子群的更新方案中对速度v进行了两次更新，第一次按照标准PSO算法中的速度公式更新速度为v'_i,j(k+1)；第二次更新按照次梯度公式更新速度为v_i,j(k+1)。最后，根据v_i,j(k+1)给出的方向，使得x_i,j(k)的位置移动至x_i,j(k+1)。

通过以上步骤，完成含储能装置的微电网并网优化调度过程。

本发明一种基于改进次梯度粒子群的微电网并网优化调度方法，通过对标准粒子群算法中的惯性权重、加速因子的改进，引入了次梯度优化机理，使得粒子群的位置和速度往好的方向变化，具有全局收敛性；使粒子不易陷入局部最优；具有收敛速度快与寻优效果好的特点；能对微电网的优化调度进行较好的优化，能有效提升微电网系统的运行效果。

附图说明

图1为本发明算法流程图。

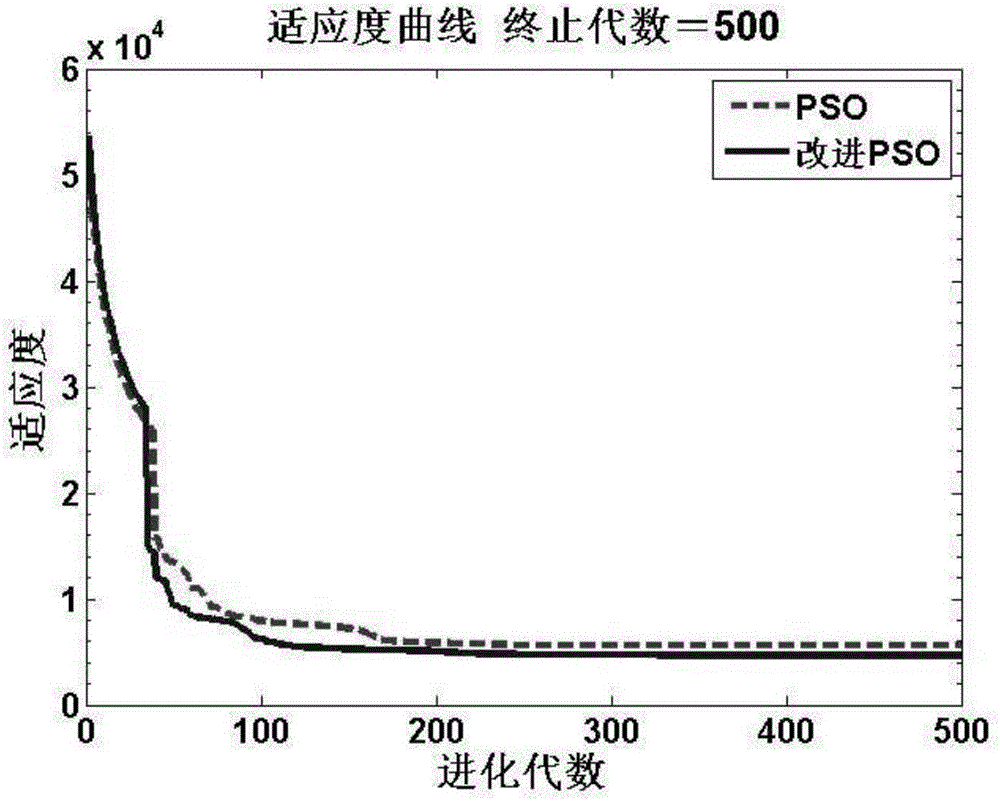
图2为两种算法的收敛性比较图。

图3为负荷、风力、光伏的预测曲线图；

其中：1—负荷；2—风力；3—光伏。

图4为微型燃气轮机出力曲线图。

图5为储能装置的出力柱状图。

图6为与大电网交互的购售电功率柱状图。

具体实施方式

如图1所示，一种基于改进次梯度粒子群的微电网并网优化调度方法，包括以下步骤：

步骤1：含储能装置的微电网并网模型建立：根据实际情况，以微电网总的发电成本和环境污染治理成本最小，建立优化调度目标函数：

上式中，微电源的燃料成本为微电源运行维护费用为与电网交互成本为N为微电源个数；c_i为第i个微电源的燃料费用单价；m_i为第i个微电源的运维费用；p_i为第i个微电源的发电量；n为调度周期；c_b,i为i时段向大电网购电价格；c_p,i为i时段向大电网售电价格；p_b,i为i时段向大电网的购电电能(kW·h)；p_p,i为i时段向大电网的售电电能(kW·h)；；M为排放气体种类数(NO_X,SO₂,CO₂)；ω_i,j为第i个微电源产生的第j种排放气体污染物系数；α_j为第j种污染气体单位排放量的治理费用。

步骤2：确立微电网系统中的运行约束条件，如下：

(1)系统功率平衡约束：

P_load＝P_pv+P_wind+P_MT+P_grid+P_BA

式中：P_load为微电网中负荷所需的总功率；P_pv、P_wind分别为微电网中光伏和风力的输出功率；P_MT、P_grid、P_BA分别为系统对微型燃气轮机、电网和蓄电池的优化功率。

(2)蓄电池充放电功率约束条件：

式中：P_c,i为蓄电池在第i时段的充电功率；P_c,max、P_c,min为蓄电池充电功率的最大、最小值；P_f,i为蓄电池在第i时段的放电功率；P_f，max、P_f，min为蓄电池放电功率的最大、最小值。

(3)微电源的输出功率限制：

式中：P_MT为微型燃气轮机的实际输出功率；分别为微型燃气轮机输出功率的上、下限。

(4)微电网与大电网交互的购售电约束：

式中：P_b、P_s分别为微电网向大电网购、售电量；P_b,max、P_b,min分别为购电的上下限；P_s,max、P_s,min分别为售电的上下限。

步骤3：对标准粒子群算法进行改进：

步骤3.1：标准粒子群算法：

速度更新公式如下：

v_i,j(k+1)＝ωv_i,j(k)+c₁r₁[p_i,j-x_i,j(k)]+c₂r₂[p_g,j-x_i,j(k)]

位置更新公式如下：

x_i,j(k+1)＝x_i,j(k)+v_i,j(k+1)

式中：j＝1,2,…,n；ω为惯性权重；r₁,r₂为[0，1]范围内的均匀随机数；c₁,c₂为非负常数，称为学习因子。

步骤3.2：对标准粒子群算法的改进：

(1)惯性权重的改进：

惯性权重ω体现的是粒子当前速度继承先前速度的重要要程度。一个较大的惯性权重有利于全局搜索，而一个较小的惯性权重则更利于局部的搜索。为了更好的平衡全局搜索与局部搜索，本发明采用线性递减惯性权重：

ω(k)＝ω_star-(ω_star-ω_end)×k/T_max

式中：ω_star为初始惯性权重；ω_end为最大迭代次数时的惯性权重；k为当前迭代次数；T_max为最大迭代次数。

(2)加速因子的改进：

参数c₁决定粒子个体历史对运动轨迹的影响，c₂决定种群的全局经验对运动轨迹的影响。在标准粒子群算法中，c₁、c₂的取值一般为固定值。本发明采用时变加速因子：

c₁＝(c_1f-c_1e)×cos(kπ/T_max)+c_1e

c₂＝(c_2f-c_2e)×cos(kπ/T_max)+c_2e

式中：c_1e,c_1f,c_2e,c_2f分别表示c₁,c₂在优化过程开始和结束的取值。其中k为当前迭代次数，T_max为最大迭代次数。由c₁＝c₂，可得因此，当时，c₁>c₂，此时是让粒子尽量多的向最优pbest学习，使粒子的全局搜索能力增强；当时，c₁<c₂，此时使粒子向社会最优位置gbest的局部靠拢，使得局部搜索得到增强。

(3)基于次梯度的PSO算法：

基于次梯度的粒子群算法其主要思想是通过沿次梯度的反方向(负次梯度方向)搜索以找到目标函数的极小值。

x_k+1＝x_k-η_k·g_k

上式中，g_k是x_k上的一个次梯度，η_k为步长函数。由于负梯度的方向不一定是函数的下降方向。因此，通过如下的最小化函数加以保证：

其中是第k步迭代时的最佳函数值。

通过对传统粒子群算法的的速度更新公式进行修正，可以得到如下基于次梯度粒子群的更新方案：

基于次梯度粒子群的更新方案中对速度v进行了两次更新，第一次按照标准PSO算法中的速度公式更新速度为v'_i,j(k+1)；第二次更新按照次梯度公式更新速度为v_i,j(k+1)。最后，根据v_i,j(k+1)给出的方向，使得x_i,j(k)的位置移动至x_i,j(k+1)。

通过以上步骤，完成含储能装置的微电网并网优化调度过程。

实施例：

在本仿真算例中的微电网包括20kW光伏、100kW风力、100kW微型燃气轮机、20kW磷酸铁锂蓄电池储能系统，负荷常规运行在并网模式下，微电网与上级大电网有能量交互。所提算法使用了Matlab进行编程实现，仿真实验在硬件配置为i7-4790@3.6GHZ的计算机中进行。

本系统算例中微型燃气轮机、大电网交互、蓄电池每小时的功率均为可调度的决策变量，粒子维度为D＝24×3＝72。标准PSO算法与基于次梯度的改进PSO算法中的种群规模都为N＝100，最大迭代次数都设置为T_max＝500。标准PSO算法中的两个学习因子c₁＝c₂＝2，惯性权重ω＝0.8。基于次梯度的改进PSO算法中，c_1e＝2.5，c_1f＝0.5，c_2e＝0.5，c_2f＝2.5，初始惯性权重ω_star＝0.9，结束惯性权重ω_end＝0.4。

表1.改进算法前后优化结果对比

通过表1和比较图2中的两条曲线可以看出：基于次梯度的改进PSO算法相较于标准PSO算法具有较快的收敛速度和更优的求解质量。标准PSO算法在系统迭代到180次左右才得到局部最优成本(5547.57元)，而基于次梯度的改进PSO算法在迭代到110次左右就可得到最优成本(4664.53元)。由此可知：基于次梯度的改进PSO算法不仅提高了收敛速度，而且提高了改进算法的全局收敛能力。

图4给出了微型燃气轮机的出力曲线，由于微型燃气轮机的发电成本相对较高，因此应当在风机和光伏发电不能满足负荷需求时才予以使用，并且由于负荷及风机、光伏的出力不确定性，导致了微型燃气轮机有较大的功率波动情况。

图5、图6分别给出了储能装置的出力情况及微电网与大电网交互时的购售电功率情况。图5中功率正值表示储能单元充电，功率负值表示储能单元放电，可以看出在负荷高峰期，储能装置放电，在负荷低谷期，储能装置充电，起到了良好的削峰填谷作用。同时，在分布式电源如风力发电机、光伏电池组有较大波动的时候，储能装置也可以很好地起到平抑波动的作用，有效保证微电网内部的稳定性。图6中正值为微电网向大电网售电，负值为微电网向大电网购电。这表明通过微电网与大电网的交互，利用峰、谷时段的电价差获得一部分收益来降低微电网的运行成本。