随迭代和节点类型改变雅可比矩阵的牛顿法潮流计算方法与流程

本发明涉及含小阻抗支路电力系统的潮流计算方法，特别是一种电力系统的直角坐标牛顿法潮流计算方法。
背景技术：
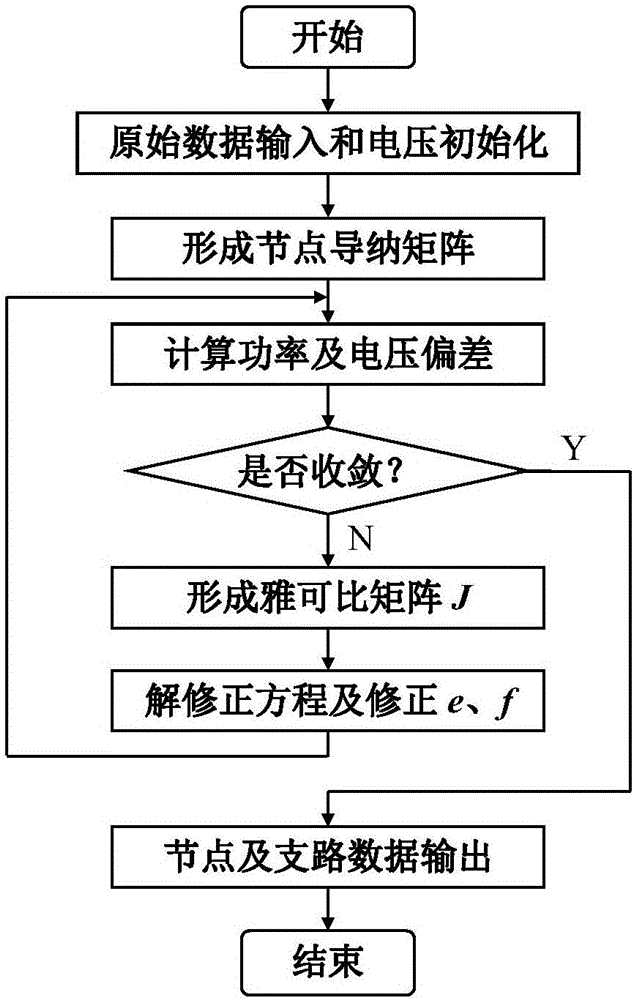
：电力系统潮流计算是研究电力系统稳态运行的一项基本计算，它根据电力系统给定的运行条件和网络结构确定整个电力系统的运行状态。潮流计算也是电力系统其他分析的基础，如安全分析、暂态稳定分析等都要用到潮流计算。由于具有收敛可靠、计算速度较快及内存需求适中的优点，牛顿法成为当前潮流计算的主流算法。牛顿法分为极坐标和直角坐标两种形式，其中直角坐标牛顿法潮流计算不需要三角函数计算，计算量相对小一些。在直角坐标牛顿法潮流计算中，节点i的电压采用直角坐标表示为：对正常电力网络，直角坐标牛顿法潮流计算具有良好的收敛性，但遇到含有小阻抗支路的病态网络时，直角坐标牛顿法潮流计算就可能发散。电力系统小阻抗支路可分为小阻抗线路和小阻抗变压器支路，在数学模型上线路可以看作变比为1:1的变压器，因此下面分析时仅以小阻抗变压器支路为例分析。小阻抗变压器模型见图1，变压器的非标准变比k位于节点i侧，阻抗位于标准变比侧。变压器阻抗zij＝rij+jxij很小，导纳为式中，yij、gjj、bjj分别为节点i和节点j之间小阻抗支路的导纳、电导和电纳；rij、xjj分别为节点i和节点j之间小阻抗支路的电阻和电抗。由于小阻抗支路lij的阻抗很小，支路的电压降也很小，因此变压器两端节点的电压应满足：如图2所示，现有直角坐标牛顿法潮流计算方法，主要包括以下步骤：A、输入原始数据和初始化电压根据电力系统节点的特点，潮流计算把电力系统节点分成3类：节点有功功率和无功功率已知、节点电压幅值和电压相角未知的节点称为PQ节点；节点有功功率和电压幅值已知、节点无功功率和电压相角未知的节点称为PV节点；节点电压幅值和电压相角已知，节点有功功率和无功功率未知的节点称为平衡节点。电压初始化采用平启动，即PV节点和平衡节点的电压实部取给定值，PQ节点的电压实部取1.0；所有电压的虚部都取0.0。这里单位采用标幺值。B、形成节点导纳矩阵设节点i和节点j原来的自电导与自电纳分别为Gi0、Bi0、Gj0、Bj0，在它们之间增加一条小阻抗支路后的自导纳和互导纳分别为：式中，Yii、Yjj分别为节点i和节点j的自导纳；Yij为节点i和节点j之间的互导纳；rij、xjj分别为节点i和节点j之间小阻抗支路的电阻和电抗；k为节点i和节点j之间小阻抗支路的变比(如果是输电线支路，变比为1)；C、计算功率及电压偏差PQ节点的功率偏差计算公式为：式中，Pis、Qis分别为节点i给定的注入有功功率和无功功率，Pis为电源有功功率与负荷有功功率之差，Qis为电源无功功率与负荷无功功率之差；ai、bi分别为节点i的计算注入电流相量的实部和虚部，为式中，n为电力系统的节点数。潮流计算收敛时，式(6)中ΔPi、ΔQi都趋近于0，因此ai和bi等于由给定值Pis和Qis计算出的ais和bisPV节点的有功功率及电压偏差计算公式为：式中，Vis为节点i给定的电压幅值。平衡节点不参与迭代计算，不需要计算功率偏差或电压偏差。平衡节点的电源有功功率和无功功率以及PV节点的电源无功功率采用式(6)计算。计算各节点功率或电压偏差的最大值，称为最大不平衡量，如果最大不平衡量的绝对值小于给定的收敛精度，转步骤F，否则执行步骤D。D、形成雅可比矩阵J雅可比矩阵J的元素(i≠j时)计算公式如下：PQ节点按式(10)-(13)计算雅可比矩阵元素；PV节点按式(10)、(11)、(14)、和(15)计算雅可比矩阵元素；平衡节点不计算雅可比矩阵元素。雅可比矩阵J的元素(i＝j时)计算公式如下：PQ节点按式(16)-(19)计算雅可比矩阵元素；PV节点按式(16)、(17)、(20)、(21)计算雅可比矩阵元素；平衡节点不计算雅可比矩阵元素。E、解修正方程及修正电压实部e、虚部f修正方程为：式中，J为雅可比矩阵。电压修正公式为：式中，上标(t)表示第t次迭代。F、输出节点及支路数据。对正常电力网络，牛顿法潮流计算具有良好的收敛性，但遇到含有小阻抗支路的病态网络时，牛顿法潮流计算就可能发散。而电力系统中小阻抗支路普遍存在，收敛性是电力系统潮流计算这类非线性问题的最重要指标，计算不收敛就无法得到方程的解。因此改善直角坐标牛顿法潮流计算针对含有小阻抗支路电力系统的收敛性具有非常重要的意义。中国专利ZL201410299531.5披露了一种通过修改常规直角坐标牛顿法潮流计算雅可比矩阵的方法，该方法计算雅可比元素时采用由给定值Pis和Qis计算的ai和bi值，改善了潮流计算的收敛性，有效解决了含有电阻为0的小阻抗支路电力系统潮流计算的发散问题。但当小阻抗支路的电阻不为0时，该方法迭代次数增加，收敛性变差，甚至不收敛。中国专利ZL201410315785.1提出了一种雅可比矩阵改变的直角坐标牛顿法潮流计算方法，该方法首次迭代和后续各次迭代采用不同的雅可比矩阵计算方法，首次迭代计算雅可比元素时采用由给定值Pis和Qis计算的ai和bi值，后续各次迭代计算雅可比元素时仍采用传统方法，有效解决了含电阻不为0的小阻抗支路电力系统潮流计算的发散问题，但该方法在电阻不为0的小阻抗支路较多时，迭代次数增加，收敛性变差。技术实现要素：为解决现有技术存在的上述问题，本发明要提出一种随迭代和节点类型改变雅可比矩阵的牛顿法潮流计算方法，该方法可以改善其分析含有电阻不为0的小阻抗支路电力系统的收敛性。为了实现上述目的，本发明根据PV节点的电源无功功率不是给定值的特点，提出了一种直角坐标牛顿法潮流计算方法来改善潮流计算收敛性。本发明的首次迭代时PQ节点采用由给定值Pis和Qis计算的ai和bi值计算雅可比矩阵元素，首次迭代时PV节点以及后续各次迭代时所有节点则采用传统方法计算雅可比矩阵元素。本发明的技术方案如下：随迭代和节点类型改变雅可比矩阵的牛顿法潮流计算方法，包括以下步骤：A、输入原始数据和初始化电压；B、形成节点导纳矩阵；C、设置迭代计数t＝0；D、计算功率及电压偏差，求最大不平衡量ΔWmax；E、判断最大不平衡量|ΔWmax|是否小于收敛精度ε；如果小于收敛精度ε，执行步骤I；否则，执行步骤F；F、形成雅可比矩阵；除首次迭代外，雅可比矩阵计算方法仍采用传统方法。首次迭代的雅可比矩阵计算方法根据节点类型采用不同方法。对于PQ节点，因潮流计算收敛时，计算功率Pi和Qi与给定值Pis和Qis相等，故采用式(8)计算注入电流相量的实部和虚部效果较好；由于PV节点的电源无功功率不是给定的，原始数据输入时该值输入是任意值，因此Qis与潮流计算收敛时的计算无功功率Qi相差很大，采用式(8)计算注入电流相量的实部和虚部效果可能较差，应该采用式(7)计算。形成雅可比矩阵元素的具体步骤如下：F1、按式(10)-(15)计算i≠j时的雅可比矩阵元素；F2、令i＝1；F3、判断是否同时满足t＝0和节点i是PQ节点的条件，如果不满足转步骤F4；如果满足，则按式(8)计算节点i的注入电流相量的实部ai和虚部bi，然后转步骤F5；F4、按式(7)计算节点i的注入电流相量的实部ai和虚部bi；F5、按式(16)-(21)计算i＝j时的雅可比矩阵元素；F6、令i＝i+1；F7、判断i是否大于节点数n，如果i不大于n转步骤F3；否则转步骤G；G、解修正方程及修正电压实部e、虚部f；H、令t＝t+1，返回步骤D进行下一次迭代；I、输出节点及支路数据。与现有技术相比，本发明具有以下有益效果：1、本发明通过在首次迭代过程中PQ节点采用与以后各次迭代过程不同的雅可比矩阵计算方法，解决了直角坐标牛顿法潮流计算在分析含有小阻抗支路电力系统时的收敛性问题。采用常规直角坐标牛顿法潮流计算不收敛时，本算法能够可靠收敛，且比现有专利技术迭代次数少。2、由于本发明不仅能有效解决常规直角坐标牛顿法潮流计算分析含有小阻抗支路电力系统的收敛性问题，同时也能对正常电力系统进行潮流计算，没有不良影响。附图说明本发明共有附图4张。其中：图1是电力系统小阻抗变压器模型示意图。图2是直角坐标牛顿法潮流计算的流程图。图3是现有发明直角坐标牛顿法潮流计算的流程图。图4是本发明直角坐标牛顿法潮流计算的流程图。具体实施方式下面结合附图对本发明进行进一步地说明。根据图1所示的小阻抗变压器模型，采用图4所示的直角坐标牛顿法潮流计算的流程图，对一个实际大型电网进行了潮流计算。该实际大型电网有445个节点，含有大量的小阻抗支路。其中，x≤0.001的小阻抗支路有49条，x≤0.0001的小阻抗支路有41条，x≤0.00001的小阻抗支路有22条。其中阻抗值最小的是节点118和节点125之间的小阻抗支路l118-125为x＝0.00000001，变比k＝0.9565，k位于节点118侧。潮流计算的收敛精度为0.00001。为了验证本发明计算含电阻不为0的小阻抗支路电力系统的收敛性，把小阻抗支路l118-125、l60-122及l287-310的电阻改为r＝0.0001。作为对比，同时采用常规直角坐标牛顿法潮流算法及现有专利算法(专利号为ZL201410315785.1)对该实际大型电网进行了潮流计算，迭代次数见表1。表1不同潮流方法的迭代结果方法常规算法ZL201410315785.1算法本发明算法迭代结果不收敛7次收敛6次收敛由表1可见，对于修改后的445节点实际电力系统算例，常规直角坐标牛顿法潮流算法不收敛，本发明算法和专利ZL201410315785.1算法都能够收敛，但本发明算法的迭代次数少1次。不同潮流计算方法各次迭代最大不平衡量见表2。单位为标幺值。表2不同潮流方法各次迭代最大不平衡量迭代序号常规算法ZL201410315785.1算法本发明算法0-4754.570367135-4754.570367135-4754.5703671351-3451593.823720038-11.138394991-3.2643685832-886651.468310079-6.163450054-0.7151480453-222023.112200678-1.441071252-0.0768472774-55754.415245002-0.106199006-0.0022945905-13972.568194423-0.006353455-0.0000174996-6386.835620506-0.000141863-0.0000000017-6585.38761914-0.0000000628-378994.7769073519-98508.02584122610-37917.863557986由表2可知，3种方法首次迭代前最大不平衡量相同且很大。首次迭代后，现有专利方法最大不平衡量明显减少，迭代7次收敛；本专利方法最大不平衡量减少速度更快，迭代6次收敛；而常规方法的最大不平衡量则变大，最终发散。PV节点的电源无功功率输入值与潮流计算的计算值及差值见表3，差值为输入值与计算值的差。单位为标幺值。表3PV节点的电源无功功率输入值与计算值及差值由表3可见，PV节点的电源无功功率输入值与潮流计算的计算值有较大的差值，有的差值达到1.6以上，用此输入值计算出的注入电流相量的实部和虚部与潮流计算收敛时的值必定有很大差距，影响潮流计算的收敛性。本算法可以采用任何一种编程语言和编程环境实现，如C语言、C++、FORTRAN、Delphi等。开发环境可以采用VisualC++、BorlandC++Builder、VisualFORTRAN等。本发明不局限于本实施例，任何在本发明披露的技术范围内的等同构思或者改变，均列为本发明的保护范围。当前第1页1 2 3