一种基于最优二矢量组合的模型预测控制方法及系统与流程

本发明属于工业自动化技术领域，更具体地，涉及一种基于最优二矢量组合的模型预测控制方法及系统。

背景技术：

目前，有很多种交流电机控制技术，如矢量控制、直接转矩控制、滑模控制和模糊控制等。但是，上述控制方法均存在一定的不足，如矢量控制动态响应慢，直接转矩控制低速特性不够理想，转矩脉动大等。模型预测控制(Model Predictive Control，MPC)诞生于上世纪70年代，随着计算机技术与微控制器的飞速发展，近年来在实时快速动态系统中的应用成为研究热点。MPC应用于永磁同步电机(Permanent-Magnet Synchronous Motor，PMSM)控制系统，能明显提高系统响应特性，抑制转矩波动、改善稳态性能、并减少逆变器开关损耗。

传统的MPC方法采用单一矢量作用于整个控制周期，系统的稳态性能较差。大量研究指出，通过增加单周期内电压矢量数目能够显著提高系统性能，常见的有基于占空比的二矢量MPC和基于电压空间矢量调制(Space Voltage Modulation，SVM)的MPC，其中SVM MPC控制方法稳态性能最优，但是，系统计算量较大、开关频率高，而且需要复杂的调制过程。基于占空比的二矢量MPC方案系统性能改善比较明显，但是已有方法采用级联策略，先选择有效矢量，再选择零矢量，最后计算占空比，没有同时考虑矢量组合在所有的占空比下的作用效果，输出矢量并非最优，对系统稳态性能提升不够理想，造成较大的电流纹波。

因此，MPC方法通过增大预测域，能够进一步提高系统性能。状态预测、代价函数和占空比计算在所有的组合中进行，计算量随着预测步长的增大而呈指数增加，过大的计算量使得MPC算法在工业应用中尤为困难。

技术实现要素：

针对现有技术的以上缺陷或改进需求，本发明提供了一种基于最优二矢量组合的模型预测控制方法及系统，以定子电流为目标基于模型预测电流控制(MPCC)，同时考虑所有可能的二矢量组合与相应作用时间下的合成矢量集合，在全部集合中选择使得代价函数最小的合成矢量，且对于MPC计算量较大的缺点，给出了可行的快速算法。由此解决现有技术中模型预测方法中电流纹波较大以及计算量较大的技术问题。

为实现上述目的，按照本发明的一个方面，提供了一种基于最优二矢量组合的模型预测控制方法，包括：

(1)以永磁同步电机的定子电流为状态变量，结合三相两电平电压逆变器开关状态计算电流矢量和电压矢量，并通过Clarke，Park坐标变换转化到dq旋转坐标系下，利用永磁同步电机的数学模型预测下一时刻的电流矢量：i＝(0,…,7)，其中X(k)＝[i_d(k) i_q(k)]^T为k时刻的电流矢量，u_i(k)为输入变量，为对应u_i(k)的在k+1时刻的预测电流矢量，F(k)、G_C(k)和H(k)为系数矩阵；

(2)在七个电流矢量中选择两个作为第一电流矢量、第二电流矢量：则合成电流矢量为：其中，i＝1,2,…表示无限集，d为占空比，表示第一电流矢量的作用时间比例且0≤d≤1；

(3)根据合成矢量构造代价函数：(i＝1,2,…)，选出合成矢量集合中的最优合成矢量使得代价函数最小，其中，X^*(k+1)＝[i_d^*(k+1)i_q^*(k+1)]^T为k+1时刻的目标电流矢量，i_d^*(k+1)与i_q^*(k+1)为dq坐标系下电流分量的参考值。

优选地，步骤(3)具体包括以下子步骤：

(3.1)通过公式：将dq坐标系下的参考电流复矢量i_dq^*转化为dq坐标系下的参考电压复矢量v_dq^*，其中，为反电动势的估算值，为对应输入u(k-1)的预测电流矢量，R_s与L_s分别为定子电阻和定子电感，T_s为采样周期；

(3.2)将dq坐标系下的参考电压复矢量v_dq^*经过Park逆变换转化到αβ坐标系下的参考电压复矢量v_αβ^*；

(3.3)将αβ坐标系下的参考电压复矢量v_αβ^*转换到N1扇区：其中，v_N1^*为转化到N1扇区的参考电压复矢量，θ_N1^*为v_N1^*的相角，U_dc为采样的母线电压；

(3.4)将αβ坐标系中的逆变器基本电压矢量幅值进行归一化处理，得到八个归一化的基本电压矢量(i＝0,1,…,7)；

(3.5)在αβ坐标系下，从基本电压矢量中选取矢量集中的两个，结合作用时间得到五个待选二矢量组合集合；

(3.6)将五个待选二矢量组合转化为对应的五条直线：其中，占空比为0≤d≤1，与为可用的电压矢量中的两个矢量；

(3.7)计算N1扇区的参考电压复矢量v_N1^*的终点到五条直线的距离，将距离最小时对应的待选二矢量组合作为最优二矢量组合。

优选地，占空比d采用无差拍控制法求解，

优选地，将最优二矢量组合的选取和占空比计算转化到离线进行，将N1扇区内参考电压复矢量v_N1^*和相角θ_N1^*的范围分别细化为N、M等分，则参考电压复矢量v_N1^*的寻址坐标为(n,m)，其中，

v_N1^*＝r_N1^*∠θ_N1^*(0≤|r_N1^*|≤1,0≤θ_N1^*＜π/3)

离线计算得到N1扇区中所有N*M点的分布和对应的占空比，存储到两个数表中，最优二矢量组合及相应占空比通过查表直接获得。

按照本发明的另一方面，提供了一种基于最优二矢量组合的模型预测控制系统，包括：

电流矢量预测模块，用于以永磁同步电机的定子电流为状态变量，结合三相两电平电压逆变器开关状态计算电流矢量和电压矢量，并通过Clarke，Park坐标变换转化到dq旋转坐标系下，利用永磁同步电机的数学模型预测下一时刻的电流矢量：i＝(0,…,7)，其中X(k)＝[i_d(k) i_q(k)]^T为k时刻的电流矢量，u_i(k)为输入变量，为对应u_i(k)的在k+1时刻的预测电流矢量，F(k)、G_C(k)和H(k)为系数矩阵；

合成电流矢量生成模块，用于在七个电流矢量中选择两个作为第一电流矢量、第二电流矢量：则合成电流矢量为：其中，i＝1,2,…表示无限集，d为占空比，表示第一电流矢量的作用时间比例且0≤d≤1；

最优合成矢量选择模块，用于根据合成矢量构造代价函数：(i＝1,2,…)，选出合成矢量集合中的最优合成矢量使得代价函数最小，其中，X^*(k+1)＝[i_d^*(k+1)i_q^*(k+1)]^T为k+1时刻的目标电流矢量，i_d^*(k+1)与i_q^*(k+1)为dq坐标系下电流分量的参考值。

总体而言，通过本发明所构思的以上技术方案与现有技术相比，主要有以下优点：

(1)以定子电流为控制对象，代价函数不受力矩、磁链及输入序列的加权系数干扰，得以简化，而且方法计算量减小，系统电流性能得到提高；

(2)不限制选出的两个矢量为有效矢量还是零矢量，同时考虑全部二矢量组合与相应的作用时间，在合成矢量集合中选取最优，消除了级联策略的局限性，为全局最优；

(3)本发明给出等效的电压方程，将电流矢量等效转化为电压矢量，进一步提出扇区变换，将电压矢量转换到指定扇区进行统一处理，很大程度地减小了计算的复杂程度；

(4)给出快速计算方案，将最优二矢量组合的选取和占空比计算转化到离线进行，采用查表法直接获取，显著减小了实时计算量；

(5)方法结构简单、实时计算量小、易于实现，运用于PMSM控制系统，电机动态响应速度快，定子电流纹波和畸变小，逆变器开关频率相对较低，系统动态和稳态性能优异。

附图说明

图1为本发明实施例公开的一种基于本发明MPC方法的PMSM控制系统的结构示意图；

图2为本发明方法的流程示意图；

图3为三相两电平电压逆变器的输入量电压矢量图；

图4为dq坐标系中待选的最优二矢量组合示意图；

图5为αβ坐标系中待选的最优二矢量组合示意图；

图6为αβ坐标系中最优组合选择示意图；

图7为快速算法分块示意图；

图8为快速算法的流程图；

图9为基于最优二矢量组合MPC方法的PMSM系统实验输出信号波形图；

图10为PMSM系统全速度范围电流纹波趋势图；

图11为本发明实施例公开的一种基于最优二矢量组合的模型预测控制系统的结构示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

图1为基于本发明MPC方法的PMSM控制系统的结构图。系统采用i_d^*＝0控制方式，速度环使用PI控制器，输出作为定子电流参考值i_q^*。采样电机转子速度ω、位置信号θ，定子电流i_abc和直流母线电压U_dc，结合开关状态S_abc计算电流和电压矢量，并通过Clarke，Park坐标变换到dq旋转坐标系下；依据PMSM系统模型预测下一时刻电流矢量然后遍历开关状态集合，选择使得代价函数最小的二矢量组合与占空比，并在下一个控制周期作用于系统。

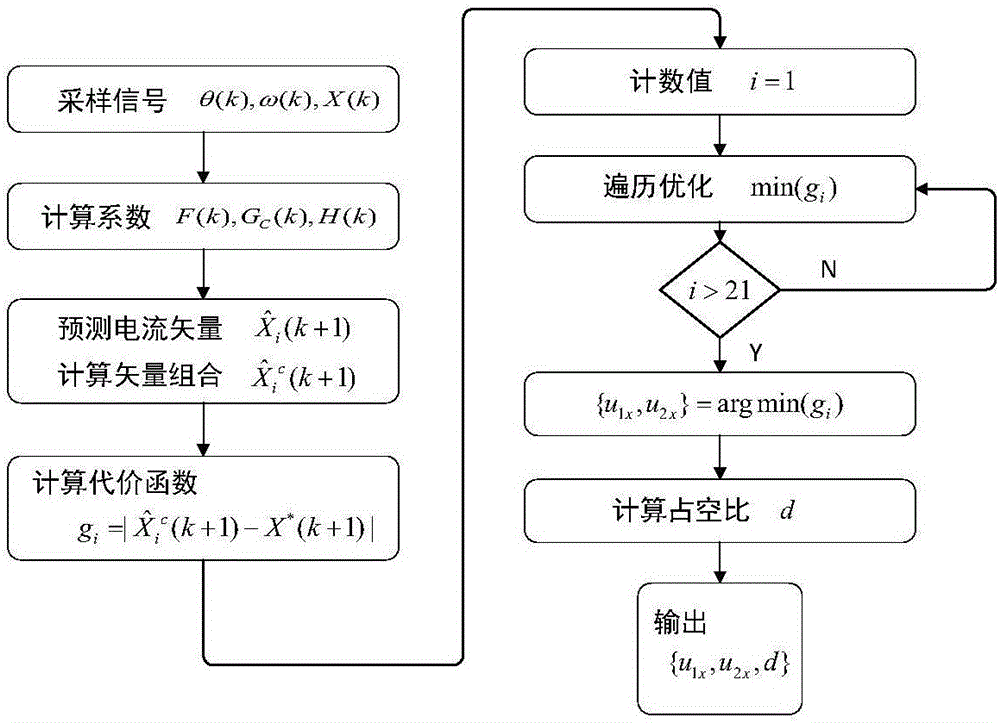
图2为本发明实施例公开的一种基于最优二矢量组合的模型预测控制方法的流程示意图，在图2所示的方法中包括以下步骤：

(1)以永磁同步电机的定子电流为状态变量，结合三相两电平电压逆变器开关状态计算电流矢量和电压矢量，并通过Clarke，Park坐标变换转化到dq旋转坐标系下，利用永磁同步电机的数学模型预测下一时刻的电流矢量：i＝(0,…,7)，其中X(k)＝[i_d(k) i_q(k)]^T为k时刻的电流矢量，u_i(k)为输入变量，为对应u_i(k)的在k+1时刻的预测电流矢量，F(k)、G_C(k)和H(k)为系数矩阵。

其中，系数矩阵F(k)、G_C(k)和H(k)的计算方式为：

G_c(k)＝U_dcC_parkC_clarke

H(k)＝[0 -T_sω(k)φ_f/L_s]^T

R_s，L_s分别为定子电阻和定子电感；ω(k)为转换到定子侧的转子角速度；T_s为采样周期，U_dc为采样的母线电压；C_park、C_clarke分别为Park变换系数和等幅值Clarke变换系数。

图3为三相两电平电压逆变器的输入量即基本电压矢量图。定义S_x,(x＝a,b,c)为逆变器开关状态，理想情况下，每一桥臂上下开关管互补导通，S_x,(x＝a,b,c)为二值函数。定义S_x＝1表示相应桥臂上管开通下管关断，S_x＝0表示相应桥臂上管关断下管开通。从图3可以看出，输入变量u_i(k)与基本电压矢量v_i一一对应，u(k)＝[S_a S_b S_c]^T。

(2)在七个电流矢量中选择两个作为第一电流矢量、第二电流矢量：则合成电流矢量为：其中，i＝1,2,…表示无限集，d为占空比，表示第一电流矢量的作用时间比例且0≤d≤1。

在选取两个电流矢量时，不限制选出的两个矢量为有效矢量或零矢量，在七个电流矢量中任意选取两个，构成全部的二矢量组合，每个矢量组合结合相应的作用时间得到合成矢量集合，同时考察矢量组合和相应的作用时间的影响，方法性能达到最优。

(3)根据合成矢量构造代价函数：选出合成矢量集合中的最优合成矢量使得代价函数最小，其中，X^*(k+1)＝[i_d^*(k+1)i_q^*(k+1)]^T为k+1时刻的目标电流矢量，i_d^*(k+1)与i_q^*(k+1)为dq坐标系下电流分量的参考值。

其中，在获取使得代价函数最小的合成矢量时，不需要对所有的二矢量组合进行判断，从所有的二矢量组合中选出待选二矢量组合，待选二矢量组合的选取方式为：定义εX_i为电流矢量的增矢量，εX^*为参考矢量的增矢量，表达式为：

εX^*＝X^*(k+1)-X(k)

定义σX_i为矢量εX^*到矢量εX_i的夹角，正负代表超前与滞后关系：

当矢量εX_1x和矢量εX_2x位于参考矢量εX^*两侧，且夹角小于π时，两矢量为待选二矢量组合，即：

然而，在目前的方式中，均是直接以dq坐标系下的电流矢量来选取最优矢量组合，需要判断某两个矢量是否为待选二矢量组合，方法比较复杂；若将全部21组二矢量作为待选二矢量组合，则遍历计算量较大，图4为在dq坐标系中待选的二矢量组合示意图，图中标号1至8的八条虚线表示有效的二矢量组合在不同的占空比下合成的矢量集合。

为了简化计算过程，本发明实施例中，步骤(3)具体包括以下子步骤：

(3.1)通过公式：将dq坐标系下的参考电流复矢量i_dq^*转化为dq坐标系下的参考电压复矢量v_dq^*，其中，为反电动势的估算值，为对应输入u(k-1)的预测电流矢量，R_s与L_s分别为定子电阻和定子电感，T_s为采样周期；

(3.2)将dq坐标系下的参考电压复矢量v_dq^*经过Park逆变换转化到αβ坐标系下的参考电压复矢量v_αβ^*；

(3.3)将αβ坐标系下的参考电压复矢量v_αβ^*转换到N1扇区：其中，v_N1^*为转化到N1扇区的参考电压复矢量，θ_N1^*为v_N1^*的相角，U_dc为采样的母线电压；

图5为αβ坐标系中待选的二矢量组合示意图，θ_N1^*为θ^*与扇区的函数，由表1给出。

表1

(3.4)将αβ坐标系中的逆变器基本电压矢量幅值进行归一化处理，得到八个归一化的基本电压矢量(i＝0,1,…,7)；

表2所示为归一化的八个基本电压矢量表达式。

表2

(3.5)在αβ坐标系下，从基本电压矢量中选取矢量集中的两个，结合作用时间得到五个待选二矢量组合集合；

(3.6)将五个待选二矢量组合转化为对应的五条直线：(i＝1,2,…,5)，其中，占空比为0≤d≤1，与为可用的电压矢量中的两个矢量；

图6为一种αβ坐标系中最优组合选择示意图。通过扇区变换，待选二矢量组合集合转化为固定的五条直线l_i(i＝1,2,…,5)：

(3.7)计算N1扇区的参考电压复矢量v_N1^*的终点到五条直线的距离，将距离最小时对应的待选二矢量组合作为最优二矢量组合。

优化原则转化为寻找目标矢量终点v_N1^*到五条直线的距离最小者：(i＝1,2,…,5)，其中δ_i为目标矢量终点v_N1^*到第i条直线的距离：

表3给出了N1扇区映射到原扇区后集合l_i在各个扇区对应的最优二矢量组合。

表3

基于最优二矢量组合MPC方法先得到转换到N1扇区的参考电压矢量v_N1^*，然后计算参考电压矢量v_N1^*终点与五条直线的距离并选出最优二矢量组合，最后计算得到矢量作用占空比。优化和占空比计算量相对较大，给出快速计算方案，将最优二矢量组合的选取和占空比计算转化到离线进行。图7为快速算法分块示意图。N1扇区中由五条线l_i(i＝1,2,…,5)划分为三个三边形和一个四边形共四个区域，每个区域的夹角平分线即图中虚线将扇区划分为九个子块B_i,(i＝1,2,…,9)。任一子块都包含了一个待选集合l_i即为该子块对应的最小距离的集合。例如子块B₁、B₅内的点到直线l₁的距离最小，对应最优矢量集合为直线l₁。子块B_9-1和B_9-2最优矢量集合与B₉相同均为l₃，表4给出了子块对应最优矢量集合。边界c₁以外的占空比不在查表范围之内，计算公式调整如下所示：

表4

将N1扇区内电压幅值v_N1^*和相角的范围θ_N1^*分别细化为N、M等分，则参考电压矢量的寻址坐标为(n，m)：

v_N1^*＝r_N1^*∠θ_N1^*(0≤r_N1^*≤1，0≤θ_N1^*＜π/3)

离线计算得到N1扇区中所有N*M点的分布区和对应的占空比，存储到两个数表中。则v_N1^*的最优矢量组合及相应占空比通过查表直接获得。图8为快速算法的流程图。

将本发明提供的基于最优二矢量组合的模型预测控制方法应用于PMSM调速系统实验。系统基于TI公司提供的TMS320F28335型号的DSP芯片实现，电机速度采用闭环PI控制器调节。实验配置及电机参数由表5给出。

表5

图9为本发明最优二矢量组合方法应用于PMSM系统实验输出信号波形图。给定速度为1500rpm，电机由静止开始启动，快速稳定状态。四个子图依次为定子电流q轴分量i_a及相应给定值i_q^*；定子电流d轴分量i_d及给定值i_d^*；电机转速n和定子A相电流i_A。从图9可以看出速度曲线平滑，超调很小；电流完全跟随指令电流，波形平滑，正弦性好；系统动态、稳态性能良好。

图10为基于本发明MPC方法的PMSM系统全速度范围电流纹波趋势。纹波有效值计算公式为：

其中为电流平均值。由实验结果可知，新方法在极低速下能够正常运行，高速段性能更优，PMSM系统全速度范围稳定运行，纹波较小，系统性能优良。

图11为本发明实施例公开的一种基于最优二矢量组合的模型预测控制系统的结构示意图，在图11所示的系统中包括：

电流矢量预测模块，用于以永磁同步电机的定子电流为状态变量，结合三相两电平电压逆变器开关状态计算电流矢量和电压矢量，并通过Clarke，Park坐标变换转化到dq旋转坐标系下，利用永磁同步电机的数学模型预测下一时刻的电流矢量：i＝(0，…，7)，其中X(k)＝[i_d(k) i_q(k)]^T为k时刻的电流矢量，u_i(k)为输入变量，为对应u_i(k)的在k+1时刻的预测电流矢量，F(k)、G_C(k)和H(k)为系数矩阵；

合成电流矢量生成模块，用于在七个电流矢量中选择两个作为第一电流矢量、第二电流矢量：则合成电流矢量为：其中，i＝1，2，…表示无限集，d为占空比，表示第一电流矢量的作用时间比例且0≤d≤1；

最优合成矢量选择模块，用于根据合成矢量构造代价函数：(i＝1，2，…)，选出合成矢量集合中的最优合成矢量使得代价函数最小，其中，X^*(k+1)＝[i_d^*(k+1) i_q^*(k+1)]^T为k+1时刻的目标电流矢量，i_d^*(k+1)与i_q^*(k+1)为dq坐标系下电流分量的参考值。

其中，各模块的具体实施方式可以参照方法实施例中的表述，本发明实施例将不作复述。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。