基于分区组合Kruskal算法的海上风电场拓扑设计方法与流程

本发明属于电源规划领域，具体涉及基于分区组合Kruskal算法的海上风电场拓扑设计方法。

背景技术：

能源问题愈发严重的今天，风力发电已被诸多国家重视并开发，研究也趋于成熟，已经成为了新能源发电的最重要形式之一。而海上风能相比于陆地风能更是具有风速稳定、单机效率高等优点，是未来新能源体系中不可替代的组成部分。但由于海上风电场成本十分高昂，维护难度大，因此如何提高海上风电场的技术经济价值是促使海上风能被大量利用的必要条件。

针对现有海上风电场规划设计中普遍采用典型放射形或其它规则排列的拓扑结构设计可能造成集电线路成本不经济的问题，可以采用基于Kruskal最小生成树原理的风电场内部拓扑优化方法。首先对海上风电场内部拓扑结构进行了分析，根据现今海上风电场内部拓扑结构设计的冗余与不足点，可采用基于Kruskal算法的海上风电场拓扑结构优化方法，能够减小海上风电场内部拓扑的电缆总成本。

然而，标准Kruskal算法直接应用于风电场拓扑结构计算中可能出现线路载流量过于集中的问题，是海上风电场拓扑结果设计中亟待解决的难题。

技术实现要素：

为了解决上述现有技术存在的问题，本发明的目的在于提供基于分区组合Kruskal算法的海上风电场拓扑设计方法，对使用标准Kruskal算法的数据进行预处理，将风机划分区域后再进行Kruskal计算来保证每个区的汇流线载流量都不会超过线路最大载流量。

为达到以上目的，本发明采用如下技术方案：

基于分区组合Kruskal算法的海上风电场拓扑设计方法，其特征在于：对使用标准Kruskal算法的数据进行预处理，将风机划分区域后再进行标准Kruskal计算，来保证每个区的汇流线载流量都不会超过线路最大载流量，即通过预先对待求拓扑结构中的风机进行逐一分区降低汇流到母线时电缆的载流量，使其满足要求。

所述基于分区组合Kruskal算法的海上风电场拓扑设计方法，包括以下步骤：

步骤一：将风机位置录入，形成路径权重集，录入载流量限制，设置分区节点数；即预先录入线路预期最大载流量为k台风机发出的功率量，由于标准Kruskal算法得出的结果必定会将树的所有节点通过一根线连接至汇流母线，则对于总风机数为m的风电场划分的区域数n即是m/k的值，m/k的值小数直接进位，再将树的所有节点平均分布到各个分区，即能够保证每个分区中的节点数都不超过允许的最大载流量；

步骤二：对第i个分区M_i排列组合分配节点；

步骤三：判断是否i＝n，如果不满足，令

其中，i为标记当前需要排列组合的分区，初值为1，M为可分配节点集，用于记录每次分配时还可供M_i分区选取的节点，初始化后为初始节点集，n为总分区数；即对分区号i和可分配节点集M进行更新；同时返回步骤二；

步骤四：对分区逐一使用标准Kruskal算法计算在本次为最优解时记录树；标准Kruskal算法为：初始化计算数据，主要是录入所有节点的坐标与节点间的路径权重，形成初始路径权重集，并建立已选节点集与已选路径集供储存计算结果备用；根据上述初始化的结果，从路径权重集中挑选权重最小的路径加入已选路径集，将该路径连接起来的点加入已选节点集；对每一个已经由多个节点和路径组成起来的树，将除了已选路径以外其他节点之间的路径从路径权重集中删除，以防止形成环网；重复上述选取最小路径和更新路径权重集的步骤，直到所有节点都加入到已选节点集中；这时已选路径集中的路径即为加权连通图最小生成树的所有路径；

步骤五：判断排列组合是否枚举完毕，如果不满足，令i＝1，并重置M为初始节点集，返回步骤二；

步骤六：输出结果最小生成树。

本发明将标准Kruskal算法的节点集根据电缆线路能够承受的载流量预先进行分区，再进行Kruskal计算，这种方法在进行Kruskal算法计算之前就先杜绝Kruskal算法的汇流过载问题，同时这也是均匀化电缆线路载流量最简单的方式。

下面通过附图和实施例，对本发明的技术方案做进一步的详细描述。

附图说明

图1为基于分区组合Kruskal算法的海上风电场拓扑设计方法流程图。

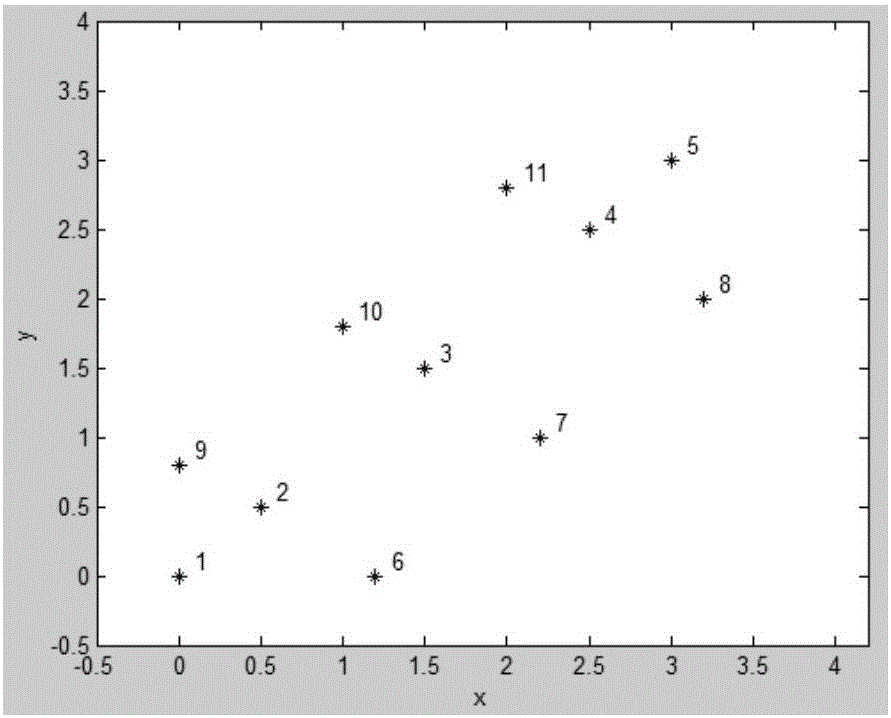
图2为算例风机位置排布情况。

图3为典型海上风电场的风机拓扑。

图4为标准Kruskal算法设计的海上风电场的风机拓扑。

图5为分区组合Kruskal算法设计的海上风电场的风机拓扑。

具体实施方式

以下结合附图及详细模型构建原理，对本发明作进一步的详细描述。

算例风机排布情况如图2，该风电场典型拓扑如图3，经过标准Kruskal算法计算后拓扑如图4，图中数字为风机编号，横纵坐标为风机所在地理位置(适用于图2‐图5)。将标准Kruskal算法拓扑与其它拓扑对比可以得到，一方面肯定了标准Kruskal算法对风电场减少电缆连接线总距离的效果，并通过计算发现了在均一网下电力系统潮流并不会受到太大影响；但另一方面也发现了应用Kruskal算法之后完全忽视了原本典型排布中各个接线可能的载流量限制与可靠性问题，由此引出本发明围绕该标准Kruskal算法采取的改进方式。

本发明设计基于分区组合Kruskal算法的海上风电场拓扑设计方法，具体流程图如图1。将标准Kruskal算法的节点集根据电缆线路能够承受的载流量预先进行分区，再进行Kruskal计算，这种方法在进行Kruskal算法计算之前就先杜绝Kruskal算法的汇流过载问题，同时这也是均匀化电缆线路载流量最简单的方式。

本发明方法会预先录入线路预期最大载流量为k台风机发出的功率量，由于标准Kruskal算法得出的结果必定会将树的所有节点通过一根线连接至汇流母线，则对于总风机数为m的风电场划分的区域数n即是m/k的值(小数直接进位)，再将节点集平均分布到各个分区，即可保证每个分区中的节点数都不超过允许的最大载流量。在计算程序中，需要对排列组合算法进行迭代的方式枚举各个区分配到不同节点的所有情况。基于分区组合Kruskal算法的海上风电场拓扑设计，得到的拓扑如图5。

对分区组合Kruskal算法拓扑进行潮流分析可得，该种算法计算出的拓扑结构同标准Kruskal排布一样，更改了分布之后对电力系统静态参数几乎没有任何影响，损耗也较标准Kruskal算法略微降低；而最重要的是，其可以按照输入的允许线路最大载流量来规划线路，这在线路载流量要求与典型排布相同时可能效果不佳，但如果线路最大载流量超过典型排布的载流量，并在降低分区数量的情况下依然满足要求，本发明方法可以有效筛选出当前不会造成线路载流量超额的电缆线最短排布。

另一方面，即使线路最大载流量在典型分布拓扑中已经到达极限值，但根据此种算法，降低少量的分区数，即提升并不多的线路载流量就可能换来更多的电缆铺设线路节省，所付出的是全网使用带载能力更高的电缆线，有效对这两个部分进行规划取舍也可换取相当的经济价值。

对于经济指标的衡量，本发明中采用电力系统成本评估中常用的等年值法来对不同拓扑结构的组网方案进行经济比较。等年值法是选取等年值费用最小的方案为最佳方案，该方案将电网设备在使用寿命内的所有费用均换算成每年等值费用。

根据经济指标模型计算可以得到不同拓扑结构的固定投资成本如表1。

由表1可以看出，虽然标准Kruskal算法排布的电缆线长度很短，但由于其对电缆线横截面规格要求很高，实际投资成本并没有显著降低，而分区组合Kruskal算法排布则在总的投资成本上明显低于典型放射链式排布和标准Kruskal算法排布。

表1不同拓扑结构固定投资成本表

同样，可以计算得到不同拓扑结构的总年损耗费用如表2，不同拓扑结构年故障损失功率与总平均功率成本如表3。

表2不同拓扑结构年损耗费用表

表3不同拓扑结构年平均功率成本表

根据以上计算结果可以看出，对于基于分区组合Kruskal算法的拓扑结构而言，其载流量与典型式大致持平，电缆线截面积小，同时还具有年故障损失功率低等特点，因此平均功率成本较其余两种排布明显降低。

和现有技术相比较，本发明具备如下优点：

(1)本发明方法考虑了线路载流量的限制：基于分区组合Kruskal算法的海上风电场拓扑设计方法可以按照输入的允许线路最大载流量来规划线路，这在线路载流量要求与典型排布相同时可能效果不佳，但如果线路最大载流量超过典型排布的载流量，并在降低分区数量的情况下依然满足要求，本发明方法可以有效筛选出当前不会造成线路载流量超额的电缆线最短排布。

(2)本发明方法具有较好的经济性：对于基于分区组合Kruskal算法的拓扑结构而言，其载流量与典型式大致持平，电缆线截面积小，同时还具有年故障损失功率低等特点，因此平均功率成本较其余两种排布明显降低。

最后应当说明的是：以上实施例仅用以说明本发明的技术方案，本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的范围内，根据本发明的技术方案及其发明构思加以等同替换或改变，都属于本发明的保护范围。