基于双极对称特征的特高压直流输电系统可靠性计算方法与流程

本发明涉及一种电力系统输电部分可靠性计算方法，特别是涉及了一种基于双极对称特征的特高压直流输电系统可靠性计算方法。
背景技术：
：我国面临着负荷中心和能源基地分布不均衡的矛盾，用电大省多集中在东南沿海一带，如珠三角和长三角地区，而能源基地多集中于中西部地区，如长江金沙江上游水能资源丰富的西南地区和煤炭资源丰富的三北地区。负荷中心“电荒”和电源中心“窝电”并存，解决这一矛盾的关键是建设特高压为主的电力输送通道，而特高压直流又以其控制方式灵活、快速，可点对点、大功率、远距离直接将电力输送至负荷中心，成为负荷中心承载区外来电的首选方案。特高压的接入对受端电网是一把双刃剑，若直流发生双极闭锁故障，会造成潮流转移和功率缺额，对受端电网产生较大的系统冲击，严重影响电网的安全稳定运行。因此，研究特高压直流输电系统的可靠性具有重要的现实意义。目前特高压直流输电系统的可靠性分析方法主要有解析法和模拟法两大类，模拟法主要是蒙特卡洛模拟，而解析法则包括频率和持续时间法、故障树分析法、串并联分析法等。但蒙特卡洛采样方法随着系统采样系统规模增大，状态评估时间明显增加；但故障树分析法不能处理多状态元件，也无法计算故障频率和持续时间；串并联分析方法无法考虑特高压直流输电系统元件受迫停运效应和恢复效应。因此基于状态空间转移的频率和持续时间方法称为特高压直流输电系统可靠性分析的主流，现有的计算方法对特高压直流输电系统进行子系统划分，充分考虑了特高压直流输电系统结构特点及多种运行方式，由换流变压器组、换流站、双极系统层层递进，充分考虑了特高压直流输电系统拓扑结构，较为准确地反映了特高压直流输电系统的实际情况。但上述模型状态空间结构复杂，状态枚举及转移时容易出现遗漏和疏忽，且计算繁杂，因此快速评估特高压直流输电系统可靠性的方法成为电力系统运行规划的需要。技术实现要素：针对上述
背景技术：
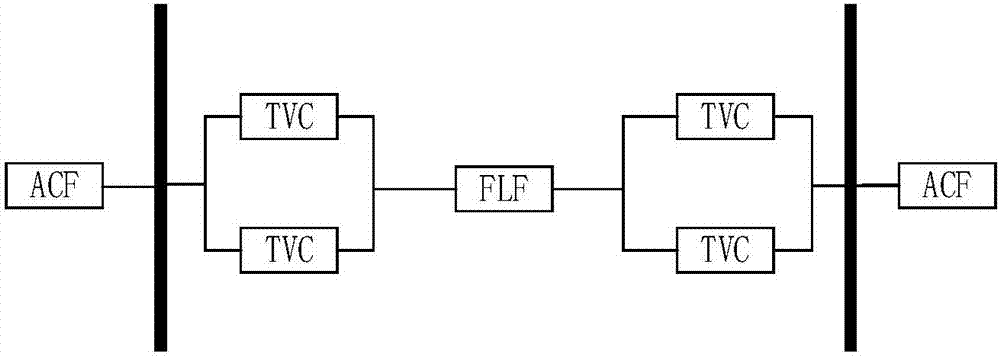
中的问题，本发明提供了一种基于双极对称特征的特高压直流输电系统可靠性计算方法，可快速评估特高压直流输电系统可靠性，便于指导电力系统调控运行。特高压直流输电系统可靠性体系众多，本发明的技术方案主要针对各容量状态概率进行计算，采用以下步骤进行计算特高压直流输电系统的可靠性结果：1)根据特高压直流输电系统拓扑结构和元件可靠性参数，串联简化得到单极模型及单极模型各组件可靠性参数。2)根据特高压直流输电系统单极等效模型，确定其状态空间模型3)根据特高压直流输电系统单极状态空间模型，可进一步推导出各容量状态转移矩阵，计算各容量状态平稳概率并进行状态合并。4)采用通用生成函数方法，综合考虑交流滤波器备用效应和备用恢复效应，计算双极系统容量状态和平稳概率。因此本发明是采用状态空间和通用生成函数结合方法，充分利用特高压直流输电系统双极对称特征，计算获得稳态概率，作为各容量状态可靠性结果，具体采用以下步骤进行计算：1)根据特高压直流输电系统的拓扑结构及其元件可靠性参数，进行串联简化获得特高压直流输电系统的单极等效模型和单极等效模型中各组件可靠性参数；原有特高压直流输电系统拓扑结构如图1所示。图中，ct为换流变压器、cv为换流阀，cc为阀控及保护装置，acf为交流滤波器acfilter，dcf为直流滤波器dcfilter，dcl为直流线路dcline。2)根据特高压直流输电系统所有可能的故障状态及其各故障状态之间的转换关系，建立特高压直流输电系统的单极状态空间模型；3)根据特高压直流输电系统的单极状态空间模型，构建包含有容量状态转移矩阵x的微分方程，再计算求得特高压直流输电系统所有可能的故障状态对应的稳态概率；4)将相同容量状态合并获得单极中正常运行换流桥个数nt对应的累计概率，再根据累计概率获得双极中正常运行换流桥个数nt’对应的稳态概率，作为特高压直流输电系统的可靠性结果。所述步骤1)具体是：对特高压直流输电系统的拓扑结构进行简化，将换流变压器ct、换流阀cv和阀控cc组合构成换流单元tvc，将直流滤波器dcf和直流线路dcl组合构成直流单元flf；并同时根据特高压直流输电系统拓扑结构中各个元件的可靠性参数采用以下公式计算获得单极等效模型中各组件的可靠性参数：λ1＝λct+λcv+λccλ2＝λacfμ2＝μacfλ3＝λdcf+λdcl+λdcf其中，λct和μct分别表示换流变压器的故障率和修复率，λcv和μcc分别表示换流阀的故障率和修复率，λcc和μcc分别表示阀控及保护装置的故障率和修复率，λacf和μacf分别表示交流滤波器的故障率和修复率，λdcf和μdcf分别表示直流滤波器的故障率和修复率，λdcl和μdcl分别表示换流变压器的故障率和修复率；λ1和μ1分别表示换流单元tvc的故障率和修复率，λ2和μ2分别表示交流单元acf的故障率和修复率，λ3和μ3表示直流单元flf的故障率和修复率。所述步骤2)具体是：2.1)将特高压直流输电单极系统所有可能的故障状态分为以下11种状态：状态1为单极等效模型中各个组件未发生故障的状态；状态2为单极等效模型仅有一侧的一个换流单元tvc发生故障的状态；状态3为单极等效模型仅有一侧的交流滤波器acf发生故障的状态；状态4为单极等效模型仅有直流单元flf发生故障的状态；状态5为单极等效模型仅有两侧的各自一个换流单元tvc发生故障的状态；状态6为单极等效模型仅有一侧的两个换流单元tvc均发生故障的状态；状态7为单极等效模型仅有一侧的一个换流单元tvc和一侧的交流滤波器acf发生故障的状态；状态8为单极等效模型仅有直流单元flf和一侧的一个换流单元tvc发生故障的状态；状态9为单极等效模型仅有一侧的两个换流单元tvc和另一侧的一个换流单元tvc发生故障的状态；状态10为单极等效模型仅有两侧的各自一个换流单元tvc和一侧的一个换流单元tvc发生故障的状态；状态11为单极等效模型仅有直流单元flf和两侧的各自一个换流单元tvc发生故障的状态；2.2)然后在状态1～状态11之间形成以下转换关系：状态1分别和状态2～状态4之间相互转换：状态1以四倍的换流单元tvc故障率λ1转换到状态2，状态2以一倍的换流单元tvc修复率μ1转换到状态1；状态1以两倍的交流单元acf故障率λ2转换到状态3，状态3以一倍的交流单元acf修复率μ2转换到状态1；状态1以一倍的直流单元flf故障率λ3转换到状态4，状态4以一倍的直流单元flf修复率μ3转换到状态1；状态2分别和状态5～状态8之间相互转换：状态2以两倍的换流单元tvc故障率λ1转换到状态5，状态5以两倍的换流单元tvc修复率μ1转换到状态2；状态2以一倍的换流单元tvc故障率λ1转换到状态6，状态6以两倍的换流单元tvc修复率μ1转换到状态2；状态2以两倍的交流单元acf故障率λ2转换到状态7，状态7以一倍的交流单元acf修复率μ2转换到状态2；状态2以一倍的直流单元flf故障率λ3转换到状态8，状态8以一倍的换流单元tvc修复率μ1转换到状态2；状态5分别和状态9～状态11之间能相互转换：状态5以两倍的换流单元tvc故障率λ1转换到状态9，状态9以两倍的换流单元tvc修复率μ1转换到状态5；状态5以两倍的交流单元acf故障率λ2转换到状态10，状态10以一倍的交流单元acf修复率μ2转换到状态5；状态5以一倍的直流单元flf故障率λ3转换到状态11，状态11以一倍的直流单元flf修复率μ3转换到状态5；状态9以一倍的换流单元tvc修复率μ1转换到状态6，状态11以两倍的换流单元tvc修复率μ1转换到状态8，状态8以一倍的直流单元flf修复率μ3转换到状态4，状态10能以两倍的换流单元tvc修复率μ1转换到状态7，状态7以一倍的换流单元tvc修复率μ1转换到状态3。获得的特高压直流输电系统的单极状态空间模型如图3所示，图中λ1表示换流单元tvc故障率，μ1表示换流单元tvc修复率；λ2表示交流滤波器acf故障率，μ2表示交流滤波器acf修复率；λ3表示直流单元flf故障率，μ3表示直流单元flf修复率，nt表示单极中状态对应的正常运行换流桥个数。所述步骤3)具体为：3.1)构建以下公式表示的包含有容量状态转移矩阵x的微分方程：其中，t表示时间，λ1表示换流单元tvc故障率，μ1表示换流单元tvc修复率，λ2表示交流滤波器acf故障率，μ2表示交流滤波器acf修复率，λ3表示直流单元flf故障率，μ3表示直流单元flf修复率；p1～p11分别表示单极等效模型为状态1～状态11的概率，k1～k11分别表示容量状态转移矩阵x对角线的第1个～第11个元素，具体采用以下公式计算：其中，xij表示容量状态转移矩阵x中第i行第j列的元素，i表示行序号，j表示列序号；3.2)将微分方程用马尔科夫逼近原理，计算求得各状态的概率p的稳定值，作为特高压直流输电系统单极等效模型所有可能的11种故障状态(状态1～状态11)对应的稳态概率ps1～ps11。所述步骤4)具体为：4.1)将状态对应的正常运行换流桥个数nt相同的状态进行合并，计算获得同一换流站的单极中正常运行换流桥个数nt对应的累计概率，具体如下：状态1对应的正常运行换流桥个数nt＝2，因此正常运行换流桥个数nt为2的累计概率pnt2计算为pnt2＝ps1；状态2、5对应的正常运行换流桥个数nt＝1，因此正常运行换流桥个数nt为1的累计概率pnt1计算为pnt1＝ps2+ps5；状态3、4、6～11对应的正常运行换流桥个数nt＝0，因此正常运行换流桥个数nt为0的累计概率pnt0计算为pnt0＝ps3+ps4+ps6+ps7+ps8+ps9+ps10+ps11；对于正常运行换流桥个数nt为0的累计概率pnt0情况，表示双极停运，考虑同一换流站中两极的交流滤波器组能够相互替换，再分为累计概率pnt0-1和累计概率pnt0-2，pnt0＝pnt0-1+pnt0-2，用于分别表示由状态3、7、10对应acf故障导致的双桥停运和状态4、6、8、9、11对应tvc故障或flf故障导致的双桥停运，累计概率pnt0-1表示由于存在交流滤波器acf故障导致的正常运行换流桥个数nt为0的累计概率，pnt0-1＝ps3+ps7+ps10；累计概率pnt0-2表示由于存在直流单元flf或者换流单元tvc故障导致的正常运行换流桥个数nt为0的累计概率，pnt0-2＝ps4+ps6+ps8+ps9+ps11。对于累计概率pnt0-1，根据交流滤波器备用效应，将不计交流滤波器故障对应的换流桥个数加以区分，再分为累计概率pnt0-11和累计概率pnt0-12，pnt0-1＝pnt0-11+pnt0-12，用于分别表示由状态3对应acf故障考虑备用效应其恢复正常运行换流桥个数nt＝2和状态7、10对应交流滤波器故障考虑备用效应其恢复换流桥个数nt＝1，累计概率pnt0-11表示由于仅交流滤波器acf故障导致的正常运行换流桥个数nt为0的累计概率，pnt0-11＝ps3；累计概率pnt0-12表示由于交流滤波器acf和换流单元tvc共同故障导致的正常运行换流桥个数nt为0的累计概率，pnt0-12＝ps7+ps10。考虑同一换流站中两极的交流滤波器组能够相互替换的情况，具体可能有如下几种：1、状态3+状态2位于同一换流站的交流滤波器组可以互为备用，如图4所示，当两极分别处于状态3和状态2时，通过调整交流滤波器的位置，可以使系统可用换流桥个数由1增加到2。因此在计算累计概率pnt0时细分为累计概率pnt0-1和累计概率pnt0-2。2、状态3+状态7通过调整交流滤波器使系统可用换流桥个数增加时，又存在不同的情况，如图5所示，当两极分别处于状态3和状态7时，通过调整交流滤波器位置，可以使系统可用换流桥个数由0增加到2。因此在计算累计概率pnt0-1时细分为累计概率pnt0-11和累计概率pnt0-12。3、状态10+状态7通过调整交流滤波器使系统可用换流桥个数增加时，又存在不同的情况，如图6所示，当两极分别处于状态10和状态7时，通过调整交流滤波器位置，可以使系统可用换流桥个数由0增加到1。因此在计算累计概率pnt0-1时细分为累计概率pnt0-11和累计概率pnt0-12。4.2)考虑同一换流站中两极各自的交流滤波器组能够相互换(同一换流站具有两极)，构建通用生成函数，并根据通用生成函数计算获得同一换流站双极正常运行换流桥个数nt’对应的稳态概率：特高压直流输电系统单极可用换流桥个数及状态概率可以使用以下通用生成函数表示为：pnt0＝pnt0-1+pnt0-2pnt0-1＝pnt0-11+pnt0-11其中，z为通用生成函数的变量值，用于区分表示正常运行换流桥个数nt的值，z2表示正常运行换流桥个数nt为2。两极为并联状态，且换流桥个数满足同样的概率分布，两极均发生交流滤波器故障导致双桥停运时，可分为两种情况：第二次交流滤波器故障发生在同侧时，两极换流桥停运；第二次交流滤波器故障发生在异侧时，由于同一极的交流滤波器组可以互为备用，特高压直流输电系统等效为单极停运，仍有两换流桥保持正常运行状态，两种情况概率相当。同时，考虑交流滤波器互为备用的恢复效应，基于并联系统通用生成函数方法，整个特高压直流输电系统正常运行换流桥个数的通用生成函数可以表示为：同一换流站双极中正常运行的换流桥个数nt’＝4对应的稳态概率计算为：pnt'＝4＝pnt22同一换流站双极中正常运行的换流桥个数nt’＝3对应的稳态概率计算为：pnt'＝3＝2pnt2pnt1同一换流站双极中正常运行的换流桥个数nt’＝2对应的稳态概率计算为：pnt'＝2＝2pnt2pnt0+2pnt1pnt0-11+pnt12+pnt0-12/2+pnt0-11pnt0-12+2pnt0-11pnt0-2同一换流站双极中正常运行的换流桥个数nt’＝1对应的稳态概率计算为：pnt'＝1＝2pnt1pnt0-12+2pnt1pnt0-2+pnt0-122/2+2pnt0-12pnt0-2同一换流站双极中正常运行的换流桥个数nt’＝0对应的稳态概率计算为：pnt'＝0＝pnt0-112/2+pnt0-122/2+pnt0-11pnt0-12+pnt0-22本发明具有以下有益效果：本发明简化了现有系统的拓扑结构，实现了快速准确评估特高压直流输电系统可靠性结果，便于指导电力系统运行规划和备用方案的制定。附图说明图1是特高压直流输电系统的主要设备及拓扑结构。图2是特高压直流输电系统的单极等效模型。图3是特高压直流输电系统的单极状态空间模型。图4是本发明方法中考虑交流滤波器互换情况之一的示意图。图5是本发明方法中考虑交流滤波器互换情况之二的示意图。图6是本发明方法中考虑交流滤波器互换情况之三的示意图。具体实施方式以下结合实施例及附图作进一步说明。采用本发明方法的实施例如下：本发明实例采用的元件可靠性参数由论文《特高压直流输电系统可靠性评估方法(现代电力,2011,28(4):1-6)》和论文《reliabilityequivalenceandsensitivityanalysistouhvdcsystemsbasedonmatrixdescriptionoff&dmethod.ieeetransactionsonpowerdelivery,2015:1-1》获得，如表1所示：表1元件故障率(次/年)修复率(次/年)换流阀0.13741460.000换流变压器0.0126290.501阀控及保护单元0.0881158.12直流滤波器和极设备0.25730输电线路4.70801101.890交流滤波器0.28761)根据特高压直流输电系统的拓扑结构及其元件可靠性参数，进行串联简化获得特高压直流输电系统的单极等效模型和单极等效模型中各组件可靠性参数：λ1＝0.2388μ1＝1114.8λ2＝0.2000μ2＝876.0λ3＝5.2080μ3＝1049.92)根据特高压直流输电系统所有可能的故障状态及其各故障状态之间的转换关系，建立特高压直流输电系统的单极状态空间模型；3)根据特高压直流输电系统的单极状态空间模型，构建包含有容量状态转移矩阵x的微分方程：再计算求得特高压直流输电系统所有可能的故障状态对应的稳态概率。p1s＝0.9938p2s＝8.464e-04p3s＝4.540e-04p4s＝0.0049p5s＝1.804e-07p6s＝9.036e-08p7s＝1.701e-07p8s＝2.037e-06p9s＝2.567e-11p10s＝2.323e-11p11s＝2.864e-104)将相同容量状态合并获得单极中正常运行换流桥个数nt对应的累计概率。pnt2＝0.9938pnt1＝8.466e-04pnt0＝0.0054pnt0-1＝4.542e-04pnt0-2＝0.0049pnt0-11＝4.540e-04pnt0-11＝0.002e-04再根据累计概率获得双极中正常运行换流桥个数nt’对应的稳态概率，作为特高压直流输电系统的可靠性。采用本发明方法进行实施和采用论文《特高压直流输电系统可靠性评估方法(现代电力,2011,28(4):1-6)》的方法作为对照，两个实施的结果如表2所示：表2换流桥个数累计概率如表3所示：表3换流桥个数nt＝4nt≥3nt≥2nt≥1nt≥0累计概率98.757％98.926％99.997％99.998％1由上述实施结果可见，本发明方法简化了现有系统的拓扑结构，可以快速评估特高压直流输电系统可靠性，还可扩展到其他领域具有双极对称性质的系统可靠性分析。当前第1页12