一种微电网数据驱动逆变器并联智能控制方法与流程

本发明属于微电网控制技术领域，特别涉及一种微电网数据驱动逆变器并联智能控制方法。

背景技术：

随着微电网技术的发展，一方面，负荷的增大要求微源提供更大的输出功率；另一方面，由于可再生能源分布相对分散、规模小、生产不连续，而传统的集中供电方式不能很好地满足这些需求，将各个逆变器系统进行并联能够实现功率分配，并且有很好的冗余性和可靠性。逆变器并联所带来的的问题是各个逆变器之间会产生环流，使逆变器的输出电能质量下降、缩短电力电子器件的寿命。

现有的逆变器并联控制方法，多采用电压电流双环和下垂控制环组成的三环结构。下垂控制根据测得的逆变器输出电压电流计算输出功率，再由pq下垂公式得到电压电流参考值，经过电压电流双环产生pwm波形来控制开关。下垂控制是通过牺牲电压水平来保证各个逆变器功率平均分配，在设计控制器时需要对系统进行建模，会有未建模动态等问题，在系统参数发生变化时控制效果变差。无模型自适应控制算法通过引入伪偏导数，把非线性系统进行线性化，然后仅仅利用系统的输入输出数据对伪偏导数实时更新，不需要对系统进行建模，为解决微电网中逆变器并联的这种复杂系统提出了新的解决思路。

此外，传统的逆变器控制方法主要有spwm、svpwm，这些方法都是根据三相相电压为调制波进行调制的，此时系统输出的三相相电压在负载以及直流侧电压中点清楚的情况下才能保证平衡，而实际的应用系统中，因为逆变系统输出三相相电压的中点与逆变器直流侧电压中点很难找到并连接，所以系统输出的真正相电压很难找到，一旦负载不平衡或者直流侧电压中点找到的有误差，即便采用先进的控制策略对系统进行调节，但因为三相电压之间有耦合的原因，所得到的三相相电压依旧是不平衡的，所以线电压也是不平衡的，即不能保证三相逆变器输出的线电压是期望的正弦波形，而在实际中虽然负载表面上所接入的是相电压，但是本质上其实是线电压，无论负载是什么特性的，只要线电压是正弦波形就能够满足要求。

技术实现要素：

本发明的目的是克服传统逆变器并联控制方法存在的未建模动态等问题，即当有外界干扰时会出现参数漂移，提出了一种微电网数据驱动型逆变器并联控制方法，来平衡各个逆变器之间的负载功率分配。同时，针对现有调制技术的不足，提出一种离散式反向线电压求解的pwm逆变器控制方法，避免负载不平衡、直流侧电压的中点找不到的问题，从而实现即便在负载不平衡的情况下，根据所需要的线电压即可达到平衡状态。

本发明提出的微电网数据驱动逆变器并联智能控制方法，包括以下步骤：

步骤1、根据下垂控制方法得到各个逆变器的控制参数初始值，也就是稳定时的输入输出数据，即：产生pwm控制脉冲的线电压形式的调制波uab、ubc、uca和输出三相线电压eab、ebc、eca，进行3s/2r变换后得到dq坐标系下的直流电压ud、uq和ed、eq，然后根据逆变器的线性化模型得到伪梯度向量的初始值φ(1)和关联矩阵p。

步骤1-1、对采集到的输入输出数据进行如下坐标变换：

式中，cz为abc坐标系到dq坐标系的正变换矩阵，θ为dq坐标系d轴与abc坐标系a轴的夹角。

步骤1-2、根据单个逆变器的线性化模型得到伪梯度向量的初始值φ(1)。

由单个逆变器线性化模型：δe＝φδu转置可得：

由于逆变器输出稳定时相邻两组数据伪梯度向量近似相等，可得：

从而得到伪梯度向量初始值：

式中，ud(m-1)、ud(m)、ud(m+1)分别为线电压调制波在m-1、m和m+1时刻d轴的值，uq(m-1)、uq(m)、uq(m+1)分别为线电压调制波在m-1、m和m+1时刻的q轴值，ed(m-1)、ed(m)、ed(m+1)分别为输出电压在m-1、m和m+1时刻的d轴值，eq(m-1)、eq(m)、eq(m+1)分别为输出电压在m-1、m和m+1时刻的q轴值。

步骤1-3、根据逆变器并联的线性化模型计算关联矩阵p。

将所得的伪梯度向量初始值φ(1)代入逆变器并联系统线性化模型δe＝φδu-pδe：

pδe＝φ(1)δu-δe(6)

令等号两边矩阵各个元素相等从而求得关联矩阵p。

式中，δe为自身逆变器输出电压和其他逆变器的差值，δu输入调制电压的变化量，δe输出电压的变化量。

步骤2、以步骤1得到的伪梯度向量初始值为初始点，利用逆变器并联系统的输入输出数据，根据通过极小化辨识准则函数：

j(φ(k))＝||e^*(k+1)-e(k+1)||²+μ||φ(k)-φ(k-1)||²(7)

式中，e^*(k+1)是逆变器输出电压参考值，e(k+1)是逆变器输出电压的实际测量值，μ是变化量的惩罚因子。

得到伪梯度向量估计值的更新公式：

即

从而在线更新伪梯度向量的估计值

式中，η∈(0,2]，δud和δuq分别是dq坐标系下k-1时刻输入调制电压的变化量，δed和δeq分别是dq坐标系下k时刻输出电压的变化量。

步骤3、根据步骤2得到的伪梯度向量估计值计算产生pwm信号的三相线电压调制波，通过极小化控制目标函数：

j(u(k))＝||e^*(k+1)-e(k+1)||²+λ||u(k)-u(k-1)||²(10)

从而得到输入调制波：

即

式中ρ∈(0,2]，λ是u(k)变化量的惩罚因子，p、δe(k)与公式(8)中定义相同。

步骤4、把步骤3中得到的输入调制信号u(k)经过2r/3s坐标变换为三相静止abc坐标系下的线电压形式uabˊ、ubcˊ、ucaˊ,通过反向线电压调制得到功率开关管的控制pwm信号。具体步骤如下：

步骤4-1、线电压uabˊ对应开关导通时间的为，在每个开关周期内，使pwm波的面积sd与正弦波面积sl相等，面积为正表示功率开关管vt1、vt6导通，面积为负表示vt3、vt4导通，功率开关管导通时间记为tab，则有：

sl＝u′ab(k)t(13)

sd＝vdctab(14)

其中，t为开关周期，uabˊ(k)为k时刻a、b相之间的线电压调制信号，vdc为直流侧电压。

步骤4-2、把线电压uabˊ分别替换为ubcˊ和ucaˊ，代入公式(15)可求得ubcˊ和ucaˊ对应的开关导通时间tbc和tca。

步骤4-3、按相位将每个一周期中线电压的波形分为6个区域，即第一区、第二区、第三区、第四区、第五区和第六区，对每个区域中的开关组合和导通时间进行说明。(定义开关状态p为逆变器的上桥臂开通，开关状态o为逆变器的下桥臂开通)

步骤4-3-1、在第一区内，易得tab>0、tbc>0、tca<0，即功率开关管vt1、vt6同时导通tab，vt2、vt3同时导通tbc，vt1、vt2同时导通tca。同一桥臂上下2个开关管不能同时导通，且每一时刻总有3个开关管工作，因此开关组合为vt1、vt6、vt2(poo)同时开通tab，vt1、vt3、vt2(ppo)同时开通tbc，剩余时间t-tab-tbc用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤4-3-2、在第二区内，易得tab<0、tbc>0、tca<0，即功率开关管vt3、vt4同时导通tab，vt2、vt3同时导通tbc，vt1、vt2同时导通tca。因此，开关组合为vt1、vt3、vt2(ppo)同时开通tca，vt4、vt3、vt2(opo)同时开通tab，剩余时间t-tab-tca用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤4-3-3、在第三区内，易得tab<0、tbc>0、tca>0，即功率开关管vt1、vt6同时导通tab，vt2、vt3同时导通tbc，vt1、vt2同时导通tca。因此，开关组合为vt4、vt3、vt2(opo)同时开通tbc，vt4、vt3、vt5(opp)同时开通tca，剩余时间t-tab-tbc用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤4-3-4、在第四区内，易得tab<0、tbc<0、tca>0，即功率开关管vt4、vt3同时导通tab，vt6、vt5同时导通tbc，vt5、vt4同时导通tca。因此，开关组合为vt4、vt3、vt5(opo)同时开通tab，vt4、vt6、vt5(oop)同时开通tbc，剩余时间t-tab-tbc用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤4-3-5、在第五区内，易得tab<0、tbc<0、tca>0，即功率开关管vt1、vt6同时导通tab，vt6、vt5同时导通tbc，vt5、vt4同时导通tca。因此，开关组合为vt1、vt6、vt5(pop)同时开通tab，vt4、vt6、vt5(oop)同时开通tca，剩余时间t-tab-tca用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤4-3-6、在第六区内，易得tab<0、tbc<0、tca>0，即功率开关管vt1、vt6同时导通tab，vt6、vt5同时导通tbc，vt2、vt1同时导通tca。因此，开关组合为vt1、vt6、vt5(pop)同时开通tbc，vt1、vt6、vt2(poo)同时开通tca，剩余时间t-tbc-tca用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤4-4、当有两个开关组合时间之和大于开关周期时，即t-tab-tbc<0，取

步骤5、将计算所得的6个区域的时间数据经过数据转换发送至dsp内的pwm中的比较寄存器，根据pwm模块内部的计数器的值和比较寄存器中的值的关系，将比较结果发送至pwm模块，产生pwm脉冲送至驱动和功率放大单元触发各个功率开关管。

步骤6、重复步骤2至步骤5得到下一时刻的伪梯度向量和线电压调制信号，再通过反向线电压调制得到pwm开关信号，直至得到理想的输出电压。

在求解伪梯度向量估计值的辨识准则函数中，对于采集的逆变器输出电压数据e(k+1)的选取，采用智能协调分析法确定数据的有效性，即是否满足使得系统趋于稳定的要求。e(k+1)数据的智能判断方法如下：

把δe＝φδu-pδe代入公式(11)中，令σ(k+1)＝e^*(k+1)-e(k+1)可得，

构造能量函数

式中，σ(k+1)为逆变器实际输出电压与参考电压的差值，l为正定实对称矩阵。然后筛选出能使为负定的输出数据。

当有逆变器并入或切除时，根据传统下垂控制方法重新获取伪梯度向量的初始值φ(1)和关联矩阵p。

在数据传输过程中，当出现数据缺失、延迟甚至错误时，可以通过已有的数据进行预估加以弥补。数据预估方案如下(以第j个逆变器在第r时刻传输的数据出现故障为例)：

在第i个逆变器的数据驱动控制模块中，利用已有的前一时刻r-1的输出数据ej(r-1)来估计ej(r)的值。由于各逆变器通过无模型自适应算法线性化得到的模型近似，所以伪梯度向量的变化也近似，利用第i个逆变器第r时刻的伪梯度向量作为第j个逆变器的伪梯度向量，求解ej(r)。

由

即得到第r时刻第j个逆变器的估计输出电压

式中，为第i个逆变器第r时刻的伪梯度向量，p为关联矩阵，δe(r)为r时刻自身逆变器输出电压和其他逆变器的差值。

本发明的有益效果为，本发明克服了传统逆变器并联控制方法存在的未建模动态等问题，平衡各个逆变器之间的负载功率分配。同时，避免负载不平衡、直流侧电压的中点找不到的问题，从而实现即便在负载不平衡的情况下，根据所需要的线电压即可达到平衡状态。

附图说明

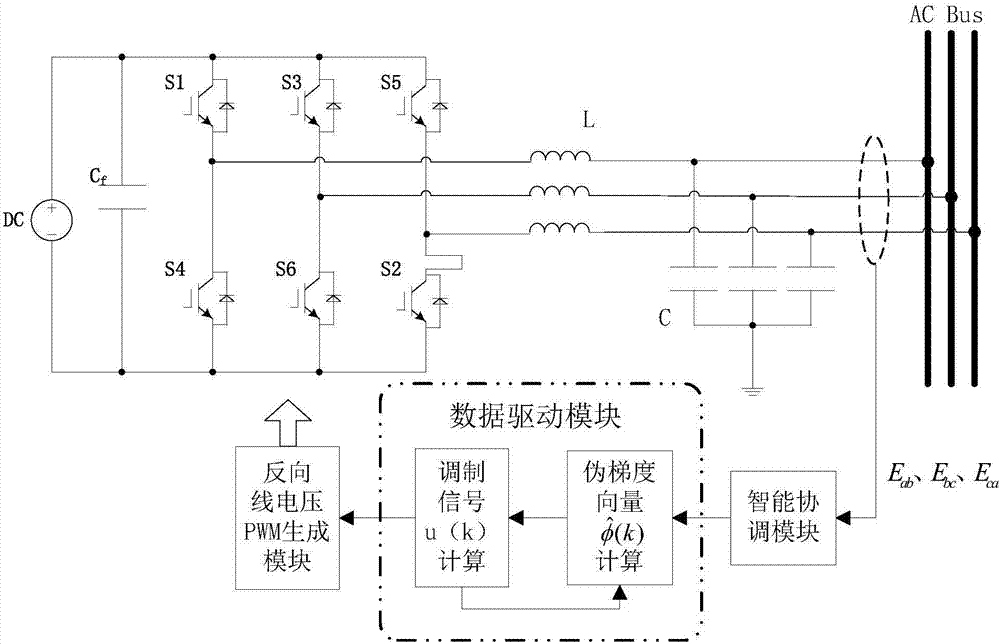
图1为本发明的数据驱动型微电网逆变器并联结构框图。

图2为本发明的带有反向线电压pwm生成器的智能数据驱动控制框图。

图3为本发明的具体的数据驱动模块控制框图。

图4为本发明的实现流程图。

图5为本发明的无模型自适应控制算法的实现流程图。

图6为本发明的坐标变换示意图。

图7为本发明的三相线电压的离散波形示意图。

图8为本发明第一区域的放大图。

图9为本发明第一区域线电压sab＝sd等效图及对应开关管的pwm波形。

图10为本发明的逆变器三相线电压输出波形。

图11为本发明的逆变器线电压uab、ubc输出波形。

具体实施方式

将本发明提出的分布式数据驱动型微电网逆变器并联智能控制方法应用于3个30kw逆变器的并联系统中，如图1和2所示，微电网交流母线电压为380v，每个逆变器控制器都采用所提出数据驱动智能控制方法，控制框图如图3所示，并且各个逆变器都通过通信总线进行数据共享。根据图4和图5将具体的控制实现步骤如下：

步骤1、根据下垂控制方法得到各个逆变器的控制参数初始值，即：产生pwm控制脉冲的线电压形式的调制波uab、ubc、uca和输出三相线电压eab、ebc、eca，经过dsp芯片tms320f28377d的a/d采样模块转换为数字信号，采样频率为10khz，在dsp中进行3s/2r变换后得到dq坐标系下的直流电压ud、uq和ed、eq，根据逆变器的线性化模型得到伪梯度向量φ(1)关联矩阵p。

步骤1-1、应用公式(1)和(2)对采集到的输入输出数据进行坐标变换。以稳定时刻t＝0.08s为例，θ＝wt＝2π×50×0.08＝8π，得到：

步骤1-2、根据单个逆变器的线性化模型得到伪梯度向量的初始值φ(1)。结合公式(3)-(5)和通过步骤1-1坐标变换输入输出数据，取不同时刻数据经过30次运算然后求平均，从而得到伪梯度向量初始值：

步骤1-3、根据逆变器并联的线性化模型计算关联矩阵p。

将所得的伪梯度向量初始值φ(1)代入逆变器并联系统线性化模型

令等号两边矩阵各个元素相等从而求得关联矩阵p。

步骤2、以步骤1得到的伪梯度向量初始值为初始点，利用逆变器并联系统的输入输出数据，根据通过极小化辨识准则函数：

j(φ(k))＝||e^*(k+1)-e(k+1)||²+μ||φ(k)-φ(k-1)||²(26)

式中，输出线电压有效值参考值设为e^*(k+1)＝380v，e(k+1)是逆变器输出电压有效值的实际测量值，μ＝1.2。

得到伪梯度向量估计值的更新公式：

从而在线更新伪梯度向量的估计值

式中，取k＝20，η＝1，根据前一时刻的输入输出数据和伪梯度向量估计值求得

步骤3、根据步骤2得到的伪梯度向量估计值计算产生pwm信号的三相线电压调制波，通过极小化控制目标函数：

j(u(k))＝||e^*(k+1)-e(k+1)||²+λ||u(k)-u(k-1)||²(29)

从而得到输入调制波：

式中ρ＝1，λ＝1.5，和是逆变器输出参考电压在dq坐标系下的分解且ed和eq是逆变器输出实测电压在dq坐标系下的分解，且k＝19时ed＝310.2117，eq＝-0.4666。

则

步骤4、把步骤3中得到的输入调制信号u(k)经过2r/3s坐标变换到三相静止abc坐标系下并转化为的线电压形式uabˊ、ubcˊ、ucaˊ,如图6所示，

通过反向线电压调制得到功率开关管的控制pwm信号。具体步骤如下：

步骤4-1、线电压uabˊ对应开关导通时间的为，在每个开关周期内，使pwm波的面积sd与正弦波面积sl相等，面积为正表示功率开关管vt1、vt6导通，面积为负表示vt3、vt4导通，功率开关管导通时间记为tab，则有：

sl＝u′ab(k)t(33)

sd＝vdctab(34)

式中，t＝0.02s为开关周期，vdc＝600v为直流侧电压。

步骤4-2、把线电压uabˊ分别替换为ubcˊ和ucaˊ，代入公式(15)可求得ubcˊ和ucaˊ对应的开关导通时间tbc＝0.0963t和tca＝0.4959t。

步骤4-3、按相位将每个一周期中线电压的波形分为6个区域，如图7所示，即第一区、第二区、第三区、第四区、第五区和第六区，对每个区域中的开关组合和导通时间进行说明。(定义开关状态p为逆变器的上桥臂开通，开关状态o为逆变器的下桥臂开通)

根据步骤4-2计算的时间大小tab<0、tbc>0、tca>0可知此时线电压在第三区，如图8和9，对开关导通时间进行求解，得到功率开关管vt1、vt6同时导通tab，vt2、vt3同时导通tbc，vt1、vt2同时导通tca。因此，开关组合为vt4、vt3、vt2(opo)同时开通tbc＝0.0963t，vt4、vt3、vt5(opp)同时开通tca＝0.4959t，剩余时间t-tab-tbc＝0.4078t用开关组合vt4、vt6、vt2(ooo)或者vt1、vt3、vt5(ppp)来补充。

步骤5、将计算所得的此时的开关导通时间数据经过数据转换发送至dsp内的pwm中的比较寄存器，根据pwm模块内部的计数器的值和比较寄存器中的值的关系，将比较结果发送至pwm模块，产生pwm脉冲送至功率放大单元触发各个功率开关管。

步骤6、重复步骤2至步骤5得到下一时刻的伪梯度向量和线电压调制信号，再通过反向线电压调制得到pwm开关信号，直至得到理想的输出三相电压，如图10和11所示。

在求解伪梯度向量估计值的辨识准则函数中，对于采集的逆变器输出电压数据e(k+1)的选取，采用智能协调分析法确定数据的有效性，即是否满足使得系统趋于稳定的要求。e(k+1)数据的智能判断方法如下：

把δe＝φδu-pδe代入公式(11)中，令σ(k+1)＝e^*(k+1)-e(k+1)可得，

构造能量函数

式中，σ(k+1)为逆变器实际输出电压与参考电压的差值，l为正定实对称矩阵。然后筛选出能使为负定的输出数据。

当有逆变器并入或切除时，根据传统下垂控制方法重新获取伪梯度向量的初始值φ(1)和关联矩阵p。

在数据传输过程中，当出现数据缺失、延迟甚至错误时，可以通过已有的数据进行预估加以弥补。数据预估方案如下(以第2个逆变器在第r时刻传输的数据出现故障为例)：

在第1个逆变器的数据驱动控制模块中，利用已有的前一时刻r-1的输出数据e2(r-1)来估计e2(r)的值。由于各逆变器通过无模型自适应算法线性化得到的模型近似，所以伪梯度向量的变化也近似，利用第1个逆变器第r时刻的伪梯度向量作为第2个逆变器的伪梯度向量，求解e2(r)。

由

即可得到第r时刻第j个逆变器的估计输出电压

式中，为第1个逆变器第r时刻的伪梯度向量，p为关联矩阵，δe(r)为r时刻自身逆变器输出电压和其他逆变器的差值。