一种基于分布式计算的输配电网一体化无功优化方法与流程

本发明涉及一种输配电网一体化无功优化方法，特别是涉及一种基于分布式计算的输配电网一体化无功优化方法，属于电力系统优化运行技术领域。

背景技术：

随着dg在配电网中渗透比例的持续增长，配电网将兼具电源接纳、电能分配、协同输电网运行的作用。配电网的运行特性和运营模式将变得日益复杂，与主网联系更加紧密，无功调节手段更加丰富。输电网无功优化不能再忽视配网的无功电压支撑作用，传统相对独立的输配电网无功优化经济性和安全性难以保证，输配电网一体化无功优化可在更大范围内实现无功资源的合理配置。基于输、配网分布自治、集中协调的管理模式，实现输配网一体化分布式无功电压控制具有重要的研究意义。

输配电网电压等级、网络结构等方面存在较大差异，管理调控分属不同控制中心。因此输配电网分布式计算需要分解协调计算。目前关于输配电网分布式无功优化有一定研究。例如：《大电网自动电压控制技术的研究与发展》(电力科学与技术学报，2007年第22卷第1期第7页)提出采用关口电压或无功功率作为协调变量的分层自动电压控制(avc)，但是此种方法不适用于大量dg接入的输配网计算。《输—配电网联合静态电压安全评估与无功优化》(山东大学，2015年)和《输配电网潮流与优化的理论研究》(山东大学，2013年)采用主从分裂法在输配电网进行了考虑双方潮流影响的协同无功优化，模型中将输配网直接分解，难以保证最优解。《coordinatedtransmissionanddistributionacoptimalpowerflow》(ieeetransactionsonsmartgrid，2016年第pp卷第99期第1页)提出广义主从算法将输配电网分解并进行分布式有功优化。该方案利用交换边界变量和乘子的方法可以一定程度上精确的全局最优解，但是边界乘子的互换对输配电网的求解算法有一定要求，对离散变量的处理也带来了一定难度。《decentralizedreactivepoweroptimizationmethodfortransmissionanddistributionnetworksaccommodatinglarge-scaledgintegration》(ieeetransactionsonsustainableenergy，2017年第1卷第8期第363页)采用广义benders分解法将输配电网无功优化问题进行分解并计算。

技术实现要素：

本发明所要解决的技术问题是：提供一种基于分布式计算的输配电网一体化无功优化方法，结合kkt最优解条件、广义主从分裂法、异步迭代分布式计算和无功优化技术对输配电网组成的全局电力系统进行无功优化。

本发明为解决上述技术问题采用以下技术方案：

一种基于分布式计算的输配电网一体化无功优化方法，所述输配电网包括一个输电网和多个配电网，各配电网和输电网之间通过各自对应的边界节点联系；包括如下步骤：

步骤1，对第k个配电网边界电压幅值和相角赋初值，根据所赋初值对输配电网进行一体化分布式潮流计算，得到潮流结果并判断潮流结果是否收敛；若不收敛则停止计算，否则输出一体化潮流边界节点状态变量k＝1,2,…,ndis，ndis为配电网的数量，开始输配电网一体化分布式无功优化计算；

步骤2，利用广义主从分裂法将输配电网一体化分布式无功优化计算模型分解为输电网无功优化、第k个配电网无功优化和边界节点信息交互三个模型；迭代次数赋初值m＝1，第k个配电网边界影响因子赋初值对应的输电网边界影响因子赋初值第k个配电网边界电压幅值、相角分别为

步骤3，根据步骤2分解得到的第k个配电网无功优化模型，采用二次罚函数-原对偶内点法进行无功优化计算，第k个配电网边界电压幅值、相角分别为输网边界影响因子取优化计算得到边界功率及配网边界影响因子并发送给输电网作为迭代数据；

步骤4，根据步骤2分解得到的输电网无功优化模型，采用二次罚函数-原对偶内点法进行无功优化计算，输电网中与各配电网对应的边界节点的负荷功率值取配电网边界影响因子取优化计算得到输电网中与各配电网对应的边界节点的电压幅值相角和输电网边界影响因子并发送给配电网作为迭代数据；

步骤5，步骤4完成后，判断边界节点的状态变量和影响因子是否收敛，若收敛则计算成功，否则m＝m+1，将步骤4计算得到的电压幅值、相角作为下一次迭代时各个配电网边界节点的电压幅值、相角，即并返回步骤3。

作为本发明的一种优选方案，步骤2所述利用广义主从分裂法将输配电网一体化分布式无功优化计算模型分解为输电网无功优化、第k个配电网无功优化和边界节点信息交互三个模型，其中输配电网分解前数学模型为：

输配电网全局无功优化目标函数为：

其中，ndis为配电网的数量，xm表示输电网内部变量向量，xpcc,k分别表示第k个配电网内部变量向量、边界变量向量，fm、分别表示输电网、第k个配电网优化的目标函数；

输电网内部等式与不等式约束为：

gm(xm)≤0

其中，hm表示输电网潮流约束，gm表示输电网的状态变量与控制变量的不等式约束；

第k个配电网内部等式与不等式约束为：

其中，表示第k个配电网潮流约束，表示状态变量与控制变量的不等式约束；

输配电网边界约束如下：

gpcc,k(xpcc,k)≤0k＝1，…，ndis

其中，hpcc,k为输电网与第k个配电网的边界等式约束条件，gpcc,k为输电网与第k个配电网的边界不等式约束条件。

作为本发明的一种优选方案，步骤2所述基于广义主从分裂法将输配电网一体化分布式无功优化计算模型分解为输电网无功优化、第k个配电网无功优化和边界节点信息交互三个模型，其中输电网分解后无功优化模型为：

其中，表示分解后的输电网目标函数，ωm表示输电网所有节点的集合，vi、vj分别表示节点i、j的电压幅值，gij表示节点i、j之间的电导，θij表示节点i、j之间的相角差，ndis为配电网的数量，xpcc,k表示第k个配电网边界变量向量，xpcc,k＝[vm,pcc,kθm,pcc,k]^t，vm,pcc,k、θm,pcc,k分别为输电网中与第k个配电网的边界节点的幅值和相角，～表示变量在该子问题求解过程中为定值，t表示转置，αk具体表示为：

其中，表示第k个配电网优化的目标函数，表示第k个配电网潮流约束，表示状态变量与控制变量的不等式约束，分别表示分解后的第k个配电网边界等式约束、不等式约束，分别为第k个配电网边界电压幅值、相角，分别表示第k个配电网的等式约束、不等式约束、边界等式约束、边界不等式约束对应的拉格朗日乘子向量；

输电网的等式与不等式约束为：

其中，pdi、qdi分别表示输电网节点i的有功、无功负荷，pgi、qgi分别表示节点i发电机的有功、无功出力，qci表示节点i电容器的无功出力，bij表示节点i、j之间的电纳；qgi,max、qgi，min分别表示节点i发电机的无功出力上、下限；tl、tl，max、tl，min分别表示支路l变压器的可调变比及其上、下限；vi,max、vi，min分别表示节点i电压的上、下限；ci、ci，maxci，min分别表示节点i电容器的档位及其上、下限。

作为本发明的一种优选方案，步骤2所述利用广义主从分裂法将输配电网一体化分布式无功优化计算模型分解为输电网无功优化、第k个配电网无功优化和边界节点信息交互三个模型，其中第k个配电网分解后无功优化模型为：

边界不等式约束包括有功、无功功率上下限：

其中，分别表示边界有功功率及其上、下限，分别表示边界无功功率及其上、下限；

配电网分解后的目标函数为：

其中，表示分解后的配电网目标函数，表示第k个配电网所有节点的集合，gab表示节点a、b之间的电导，va、vb分别表示节点a、b的电压幅值，θab表示节点a、b之间的相角差，为上次输电网迭代计算结果，表示边界优化计算结果对输网优化目标的影响，在此时为定值；

βk＝ym.pcc,k

其中，ym.pcc,k表示输电网中与第k个配网的边界等式约束对应的拉格朗日乘子，分别为第k个配电网边界有功、无功功率；

第k个配电网的等式与不等式约束为：

其中，pd,a、qd,a分别表示节点a的有功、无功负荷，pdg,a、qdg,a分别表示节点a并网dg的有功、无功出力，qc,a表示节点a处电容器的无功出力，bab表示节点a、b之间的电纳，qdg,a,max、qdg,a，min分别表示节点a处并网dg的无功出力上、下限，va,max、va，min分别表示节点a处电压上、下限；ca、ca，max、ca，min分别表示节点a处电容器的档位及其上、下限。

作为本发明的一种优选方案，步骤5所述判断边界节点的状态变量和影响因子是否收敛，其中收敛的判据为：

其中，k＝1,2,…,ndis，ndis为配电网的数量，分别为第k个配电网边界有功、无功功率，分别为第k个配电网边界电压幅值、相角，αk为第k个配电网中的配网边界影响因子，βk为输电网中与第k个配电网对应的输网边界影响因子，m+1、m、m-1均表示迭代次数，ε＝10-⁵，|·|表示绝对值。

本发明采用以上技术方案与现有技术相比，具有以下技术效果：

1、本发明将全局优化模型分解，引入边界影响因子，保证了输、配电网优化目的的一致性和同步性。

2、本发明校正环节中输、配电网无功优化的分布式计算保持了输、配电网现有的计算模式，通过pcc点处电气信息和边界影响因子的交换即可实现全网无功优化的分布式计算。

3、本发明采用罚函数规整离散变量，使得在输配网全局优化目标函数可微可分的基础上，保证了边界影响因子的计算，保证了方法的可行性和适用度。

附图说明

图1是本发明输配全局无功优化问题分解示意图。

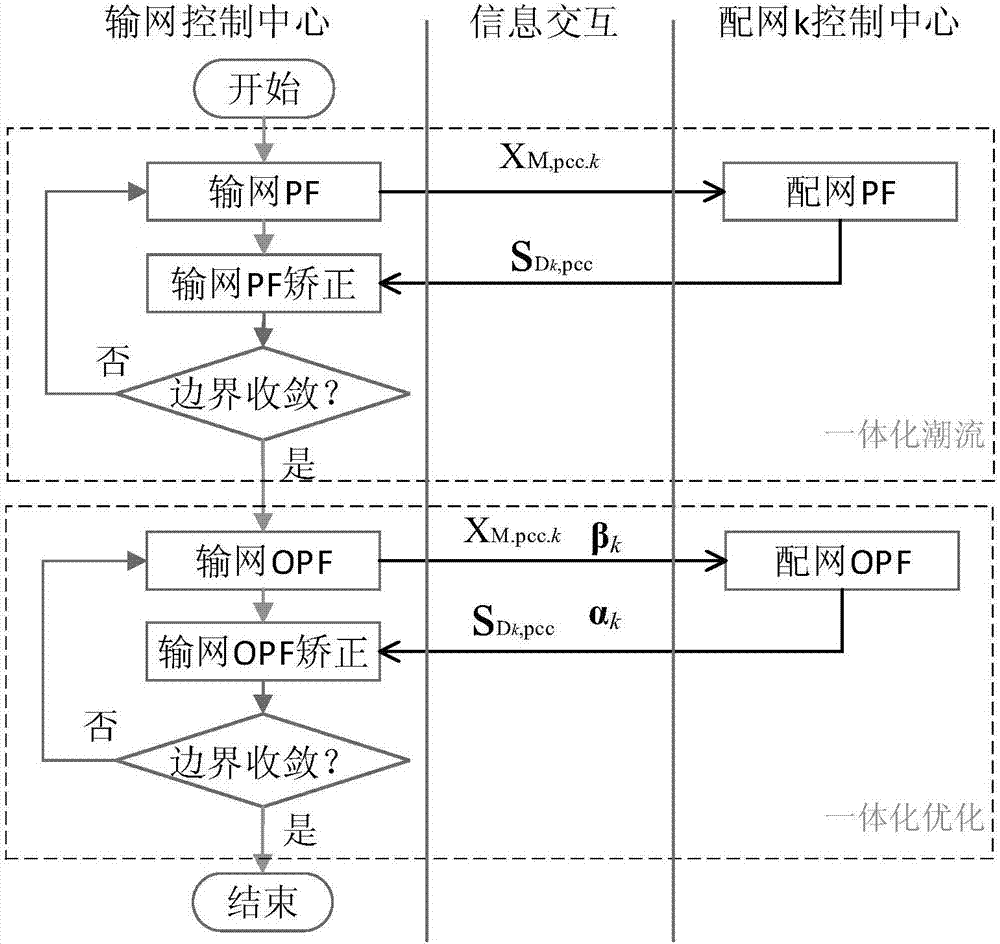
图2是本发明输配电网分布式无功优化算法流程图。

图3是独立优化、集中优化与本发明方法下的电压水平变化趋势图。

图4是独立优化、集中优化与本发明方法下的无功补偿设备投入量图。

具体实施方式

下面详细描述本发明的实施方式，所述实施方式的示例在附图中示出。下面通过参考附图描述的实施方式是示例性的，仅用于解释本发明，而不能解释为对本发明的限制。

本发明将输配电网无功优化问题分解为输电网无功优化、配电网无功优化和边界信息交互三部分，引入代表输配电网的相互影响的边界拉格朗日乘子项(简称边界影响因子)，并将边界状态变量及边界影响因子作为协同无功优化的边界协调量，采用二次罚函数-原对偶内点法分别交替求解输、配电网无功优化子问题，通过分布式迭代实现输配电网一体化无功优化计算。针对离散变量导致边界乘子无法计算的问题，本发明引入二次罚函数规整离散变量，使得在输配网全局优化目标函数可微可分的基础上，实现离散变量的处理。

如图1所示的输配电网全局无功优化问题分解图，主要包括分解前和分解后两个过程，分解前包括一个输电网(m)连接多个配电网dk(k＝1,2,…,ndis)，其边界节点简称pcc点。分解后为输电网无功优化、配电网无功优化和边界交互三个部分。具体分解过程为：

输配网分解前数学模型：

1)输配网全局无功优化目标函数为：

其中，ndis表示配电网的数量，xm、xpcc.k分别表示输网内部变量向量、配网k内部变量向量及其边界变量向量，fm、分别表示输网、第k个配网优化的目标函数。

2)输电网内部等式与不等式约束为：

gm(xm)≤0

其中，hm表示输网潮流约束，gm表示输网的状态变量与控制变量的不等式约束。将pcc点进行复制，规定xm,pcc,k与为电气上的同一点，拥有相同的电气量，xm,pcc.k、分别表示输网和第k个配网的pcc点在输、配网中的状态变量向量。

3)配网k内部等式与不等式约束为：

其中，为第k个配网潮流约束，表示状态变量与控制变量的不等式约束。

4)输配电网边界约束如下：

gpcc,k(xpcc,k)≤0k＝1，…，ndis

其中，hpcc,k为输电网与配网k的边界等式约束条件，gpcc,k为输电网与配网k的边界不等式约束条件。

全网无功优化的kkt条件分解：

1)为将输配电网潮流解耦，引入变量向量spcc.k，表示输配网边界传输功率向量。则边界等式约束hpcc,k变为：

hm,pcc.k(xm,xm,pcc.k)＝spcc.k

其中，hm,pcc.k、分别表示分解后输网、配网k边界等式约束。

2)输配网全局目标函数根据拉格朗日理论分解，下面进行分解。全网拉格朗日函数为：

其中，y、w分别表示等式、不等式约束的对偶乘子，上标t表示转置。全网取得最优解的kkt条件为：

设则全网取得最优解的kkt条件也可以写为：

若要满足上述条件，进行一阶线性近似，输、配电网目标函数改进为：

βk＝ym.pcc,k

其中，分别表示分解后的输配网目标函数，αk、βk分别称为配网边界影响因子、输网边界影响因子。可以看出，输电网目标函数的增加项αk^txpcc.k代表边界对配电网的影响，配电网的目标函数增加项βk^tspcc.k代表边界对输电网的影响。

因此通过以上处理，本发明将全局无功优化问题分解为输网无功优化子问题、配网无功优化子问题和边界一致性协调子问题。输配网可通过交换少量边界信息和有限次的迭代完成一体化分布式计算，从而达到全局的优化配置。

3)输电网分解后无功优化数学模型

输网通过调节发电机无功出力、电容器分接头及可调变压器的分接头，同时要满足无功电源出力、节点电压幅值的约束和电容器(c)、可调变压器(t)分接头位置的限制。目标函数为：

其中，vi表示节点i的电压幅值；gij、bij表示节点i、j之间的电导、电纳；θij＝θi-θj表示节点i、j之间的相角差；ωm表示输电网所有节点的集合；来自配电网上一次迭代计算结果，此时为定值，具体表示为：

xpcc,k＝[vm,pcc,kθm,pcc,k]^t

输网的等式与不等式约束为：

其中，pdi、qdi分别表示输电网节点i的有功、无功负荷，pgi、qgi分别表示节点i发电机的有功、无功出力，qci表示节点i电容器的无功出力，bij表示节点i、j之间的电纳；qgi,max、qgi，min分别表示节点i发电机的无功出力上、下限；tl、tl，max、tl，min分别表示支路l变压器的可调变比及其上、下限；vi,max、vi，min分别表示节点i电压的上、下限；ci、ci，maxci，min分别表示节点i电容器的档位及其上、下限。

输电网无功优化问题是个连续变量和离散变量共存的、非线性混合整数规划问题。离散变量的存在使边界影响因子的计算面临了困难，因此本发明采用在目标函数中加入二次罚函数项的方法迫使离散控制到达它的一个分级上，同时也可保证乘子项的计算。

4)配网k分解后无功优化数学模型

输配电网边界功率约束，配电网优化过程中，传输功率需符合以下约束，如果超过限制，采用边界值。边界不等式约束包括有功、无功功率上下限：

其中，分别表示边界有功功率及其上、下限，分别表示边界无功功率及其上、下限。配电网分解后的目标函数为：

其中，表示分解后的配电网目标函数，表示第k个配电网所有节点的集合，gab表示节点a、b之间的电导，va、vb分别表示节点a、b的电压幅值，θab表示节点a、b之间的相角差，为上次输电网迭代计算结果，表示边界优化计算结果对输网优化目标的影响，在此时为定值。

βk＝ym.pcc,k

其中，ym.pcc,k表示输电网中与第k个配网的边界等式约束对应的拉格朗日乘子，分别为第k个配电网边界有功、无功功率；

配网无功优化控制变量包括可控dg的无功出力和电容器：

其中，pd,a、qd,a分别表示节点a的有功、无功负荷，pdg,a、qdg,a分别表示节点a并网dg的有功、无功出力，qc,a表示节点a处电容器的无功出力，bab表示节点a、b之间的电纳，qdg,a,max、qdg,a，min分别表示节点a处并网dg的无功出力上、下限，va,max、va，min分别表示节点a处电压上、下限；ca、ca，max、ca，min分别表示节点a处电容器的档位及其上、下限。

本发明所涉及的基于分布式计算的输配电网一体化无功优化算法流程图如图2所示，包括如下步骤：

1)配电网k的pcc点赋电压初值(此后默认配网k＝1，…，ndis)，输配电网进行一体化分布式潮流计算。若潮流不收敛，停止计算；若收敛得到一体化潮流pcc点状态变量开始输配电网一体化分布式无功优化计算，同时赋初值：迭代次数m＝1，输、配电网边界影响因子配网边界电压幅值和相角

2)配电网进行无功优化，配网pcc点电压初值为输网边界影响因子取根据配网k无功优化问题模型，采用的罚函数-原对偶内点法进行无功优化计算，优化计算得边界功率及配网边界影响因子发给输网作为迭代数据。

3)根据输网的无功优化模型，pcc点负荷功率值取配网边界影响因子取采用罚函数-原对偶内点法进行无功优化计算。输网无功优化算得输网pcc点电压幅值和相角以及下次迭代计算的输网边界影响因子发送给配网作为迭代数据，

4)判断边界收敛条件是否收敛。若满足则计算成功；否则m＝m+1，返回2)。

其中边界收敛判据为：

其中，分别为第k个配电网边界有功、无功功率，分别为第k个配电网边界电压幅值、相角，αk为第k个配电网中的配网边界影响因子，βk为输电网中与第k个配电网对应的输网边界影响因子，m+1、m、m-1均表示迭代次数，ε为很小的数，取ε＝10^-5，|·|表示绝对值。

结果验证：为了测试本发明所提方法的有效性，应用本发明方法对ieee-30和ieee-33节点系统进行了仿真验证。为不改变原输网负荷分布，将输网pcc点的部分负荷值等效为配网系统，形成输配电网优化系统模型。输电网功率基准值为100mw，配电网电压基准值取为12.66kv，功率基准值取为10000kw，电压安全范围为0.95～1.05p.u.。由于输配电网采用的标幺值不同，因此边界乘子在进行交替迭代时也需要进行标幺值归算。

ieee30节点系统电容器调节范围标幺值为0～0.3，设为6档，每档0.05，最大、最小离散惩罚系数为100,10；变压器分接头调节范围为0.95～1.05，档位间隙0.01，最大、最小系数为200,50。

ieee33节点系统在节点4、8、15安装dg(称为dg4,dg8,dg15)，有功出力为300kw，无功出力在-300～300kvar范围内可调；29号节点接入svc，可调范围为0～300kvar；在10、24号节点接入c，调节范围标幺值为0～0.03，设为6档，每档0.005，最大、最小系数为100,10。

为验证本发明算法正确性，构建输配网集中优化算例系统(输、配网传送数据到同一控制中心优化)，从而找到具有参照性的精确最优解，为接下来的对比分析做准备。将配网网络参数标幺值归算至输网侧，其中为不改变原输网负荷分布，将输网26号节点的部分负荷值等效为配网系统，形成输配集中优化系统算例，输配电网简称m，d26。

采用集中优化、独立优化、本文一体化分布式优化三种方式分别对算例进行仿真，计算结果及对比分析见表1。独立优化表示输配网采用一体化潮流计算的边界结果分别进行无功优化，配电网控制变量初值选为调节范围上限的1/3。

表1集中、独立、一体化分布式无功优化结果对比

由表1可知，本发明优化算法和集中优化结果非常接近，证明本发明算法合理有效。相比于独立优化，本发明算法更合理地分配了无功资源，明显减少网损并提高了pcc点电压幅值。输配网可以相互支撑，增加了电网运行的安全性和经济性。给出输配电网各节点电压幅值曲线如图3所示，无功补偿设备投入对比如图4所示。由图3、图4可知，本发明算法可以在降低系统网损的同时，合理分布无功资源。

算例结果表明，本发明可以充分调度输配网无功资源，提供输配网电压水平，配网可为输电网提供无功支撑；输网也能为配网的运行提供支持；输配网一体化分布式无功优化比传统主配网独立优化更加合理，将为大量dg接入后的主配网一体化运行分析提供基础理论和技术支撑。

以上实施例仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明保护范围之内。