考虑铁损的永磁同步电机分数阶变结构模型及辨识方法与流程
本发明涉及一种考虑铁损的永磁同步电机分数阶变结构模型及辨识方法。
背景技术:
随着能源枯竭和环境污染的日益严重,电动汽车越来越备受关注,成为未来汽车发展的主要方向。电机驱动系统是电动汽车动力系统的核心部件,是动力电池的输出负载,对整车动力性、经济性和舒适性等至关重要。在电动汽车用驱动电机,如交流异步电机、直流无刷电机、开关磁阻电机、永磁同步电机、轮毂电机等,其中永磁驱动电机因具有效率高、能量密度大、响应快、调速性能好、体积小、运行可靠等众多优点,已成为当前电动汽车用驱动电机研发与应用的热点。精确的电机模型对电机本体设计和高性能电机控制器的设计意义重大,也是电动汽车电机驱动系统性能提高和效率优化的研究基础。
按不同的建模方法电机模型可以划分为不同的种类,如按模型变量,可以划分为电流模型、磁链模型和混合模型等;按电机变量变化情况,可以分为稳态模型和暂态模型;按是否考虑铁损等损耗,可以分为忽略损耗的模型和考虑损耗的模型。目前,常用的电机模型按不同研究领域主要有以下几种:①物理坐标系模型、②等效电路模型、③磁链模型、④小信号模型、⑤归一化模型、⑥空间相量模型等。其中,等效电路模型因物理意义清晰,建模分析简单,在电机系统研究,尤其是电机系统的故障研究中应用比较广泛。
然而,建立一个实用而精确的电机模型并不简单,这是因为永磁驱动电机是一个多变量、非线性、强耦合的高阶时变系统。目前传统电机等效电路模型中的电感采用的是整数阶模型,实际上,电感表现出较强的非线性特性,更适合用分数阶模型来模拟。对比整数阶模型,分数阶电机模型具有更多的自由度、更大的柔性。同时,分数阶电感的引入也增加了许多新的现象和规律,具有比传统电机模型更优的动态响应特性。
现有的模型一般不计铁心损耗,实际上,在电机稳定运行后,电机稳态效率优化成为系统考虑和关注的焦点,而铁心损耗是电机效率优化不可忽略的因素,因此单一结构模型并不能兼顾电机动态响应指标和电机效率优化的多重需求,研究如何实现模型的变结构成为必然。
技术实现要素:
本发明为了解决上述问题,提出了一种考虑铁损的永磁同步电机分数阶变结构模型及辨识方法,本发明将传统电机等效电路模型的整数阶电感推广到分数阶电感,由于增加了分数阶阶次参数,模型获得了更多的自由度、更大的柔性;同时,铁心损耗引入模型,使研究电机效率优化的模型更为精确。本发明两个模型之间通过切换控制实现模型变结构,因此模型精度更高,兼顾了模型的实用性和准确性,满足电机动态响应和效率优化的多重需求,具有较高的应用价值。
为了实现上述目的,本发明采用如下技术方案:
一种考虑铁损的永磁同步电机分数阶变结构模型,包括永磁同步电机分数阶动态等效电路模型和考虑铁损的永磁同步电机稳态等效电路模型,两个模型之间通过切换控制实现在电机动态响应性能或电机效率优化等稳态性能的研究阶段中的模型变结构;
所述动态等效电路模型和稳态等效电路模型,均包括旋转坐标系下的d轴等效电路和q轴等效电路,两个等效电路均包括依次相连的电机对应轴电压、电机定子绕组电阻、对应轴电流控制的电压源,其中,q轴等效电路还包括由转子永磁体的励磁磁通控制的电压源;
所述动态等效电路模型还包括串联在电机定子绕组电阻、对应轴电流控制的电压源之间的电机对应轴分数阶电感;
所述稳态等效电路模型还包括并联在电机定子绕组电阻、对应轴电流控制的电压源之间的电机铁心损耗电阻。
进一步的,所述动态等效电路模型的所述分数阶电感的阶次基于最小二乘法辨识模型确定。
进一步的,所述动态等效电路模型中的d轴等效电路,电路电压方程表示为
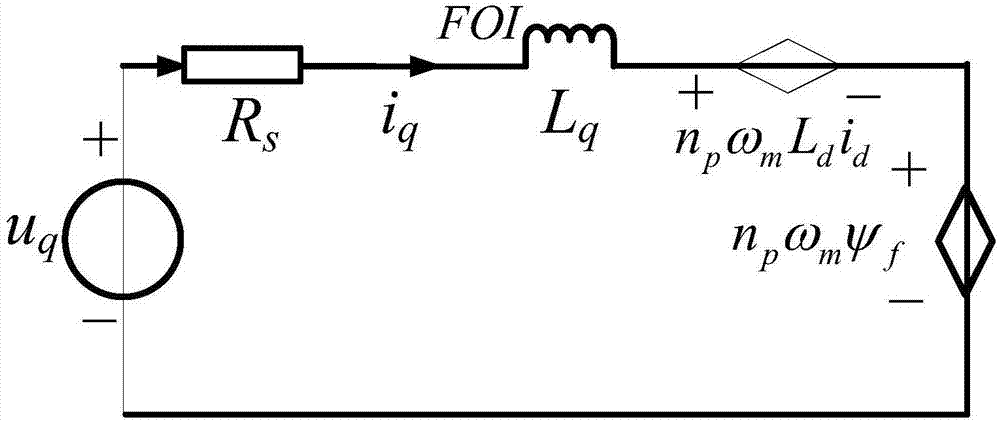
式中,ud为电机d轴电压;id、iq分别为电机d轴和q轴电流;lq分别为电机q轴分数阶电感大小;rs为电机定子绕组电阻;np为定子绕组的极对数;ωm为转子机械角速度。
进一步的,所述动态等效电路模型中的q轴等效电路,电路电压方程表示为
式中,uq分别为电机q轴电压;ψf为转子永磁体的励磁磁通。
进一步的,所述稳态等效电路模型中的d轴等效电路,电路电压方程表示为ud=rs(id+idc)-npωmlqiq=rs(id+idc)+rcidc,式中,idc为电机定子中铁心损耗电流的d轴电流分量,rc为电机铁心损耗电阻。
进一步的,所述稳态等效电路模型中的q轴等效电路,电路电压方程表示为uq=rs(iq+iqc)+npωmldid+npωmψf=rs(iq+iqc)+rciqc,式中,iqc为电机定子中铁心损耗电流的q轴电流分量。
所述动态等效电路模型的分数阶电感,利用分数阶微积分理论来描述实际电感特性的分数阶电感模型,其特性方程表示为
所述的分数阶电感的阻抗za(s),令s=jω,表示为:
所述考虑铁损的永磁同步电机分数阶变结构等效电路模型,其输出转矩表示为te=np[ψf+(ld-lq)id]iq,式中,te为电机的输出转矩。
基于上述考虑铁损的永磁同步电机分数阶变结构等效电路模型的参数辨识方法,包括以下步骤:
(1)根据分数阶微积分理论,实际的电感模型是分数阶元件,表示分数阶电感的特性方程及传递函数;
(2)分别构建永磁同步电机分数阶动态等效电路模型和考虑铁损的永磁同步电机稳态等效电路模型;
(3)通过用电桥测量三相电阻确定电机定子绕组电阻;
(4)基于电机稳态电压方程,通过电压、电流及转速数据的采集,通过稳态计算实现电机d轴和q轴分数阶电感参数的离线辨识;
(5)通过测量电压、电流和计算得到的等效电路分数阶电感得到分数阶电感的分数阶阶次;
(6)采用直接测试法,利用原动机与被测试电机对拖,利用不同负载下的测试计算电机铁心损耗,进而拟合得到电机铁心损耗电阻的变化曲线;
(7)根据得到的考虑铁损的永磁同步电机分数阶变结构等效电路模型,建立永磁同步电机分数阶动态等效电路模型和考虑铁损的永磁同步电机稳态等效电路模型两部分,两个模型之间通过切换控制实现在不同研究阶段中的模型变结构。
与现有技术相比,本发明的有益效果为:
1.本发明将传统的永磁同步电机等效电路模型推广到分数阶,并通过实验辨识模型参数和分数阶阶次,由于分数阶电感增加了分数阶阶次这一未知参数,模型获得了更多的自由度、更大的柔性;分数阶动态等效电路使得模型获得了更好的动态性能;铁心损耗引入模型,使得电机效率优化的模型更为精确。
2.本发明两个模型之间通过切换控制实现在不同研究阶段中的模型变结构,因此模型精度更高,兼顾了模型的实用性和准确性,满足电机动态响应和电机效率优化的多重需求,具有较高的应用价值。
附图说明
构成本申请的一部分的说明书附图用来提供对本申请的进一步理解,本申请的示意性实施例及其说明用于解释本申请,并不构成对本申请的不当限定。
图1为本发明永磁同步电机分数阶动态等效电路d轴模型结构示意图;表中foi表示分数阶电感;
图2为本发明永磁同步电机分数阶动态等效电路q轴模型结构示意图;
图3为本发明考虑铁损的永磁同步电机稳态等效电路d轴模型结构示意图;
图4为本发明考虑铁损的永磁同步电机稳态等效电路q轴模型结构示意图;
具体实施方式:
下面结合附图与实施例对本发明作进一步说明。
应该指出,以下详细说明都是例示性的,旨在对本申请提供进一步的说明。除非另有指明,本文使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。
需要注意的是,这里所使用的术语仅是为了描述具体实施方式,而非意图限制根据本申请的示例性实施方式。如在这里所使用的,除非上下文另外明确指出,否则单数形式也意图包括复数形式,此外,还应当理解的是,当在本说明书中使用术语“包含”和/或“包括”时,其指明存在特征、步骤、操作、器件、组件和/或它们的组合。
在本发明中,术语如“上”、“下”、“左”、“右”、“前”、“后”、“竖直”、“水平”、“侧”、“底”等指示的方位或位置关系为基于附图所示的方位或位置关系,只是为了便于叙述本发明各部件或元件结构关系而确定的关系词,并非特指本发明中任一部件或元件,不能理解为对本发明的限制。
本发明中,术语如“固接”、“相连”、“连接”等应做广义理解,表示可以是固定连接,也可以是一体地连接或可拆卸连接;可以是直接相连,也可以通过中间媒介间接相连。对于本领域的相关科研或技术人员,可以根据具体情况确定上述术语在本发明中的具体含义,不能理解为对本发明的限制。
正如背景技术所介绍的,现有技术中存在永磁驱动电机是一个多变量、非线性、强耦合的高阶时变系统,因此建立一个实用而精确的电机模型并不简单的不足,为了解决如上的技术问题,本申请提出了一种考虑铁损的永磁同步电机分数阶变结构等效电路模型及参数辨识方法,本发明将传统等效电路模型的整数阶电感推广到分数阶电感,由于增加了分数阶阶次参数,模型获得了更多的自由度、更大的柔性;同时,铁心损耗引入模型,使得电机效率优化的研究更为精确。本发明两个模型之间通过切换控制实现在不同研究阶段中的模型变结构,因此模型精度更高,兼顾了模型的实用性和准确性,满足电机动态性能指标提升和电机效率优化的多重需求,具有较高的应用价值。
本发明公开的一种考虑铁损的永磁同步电机分数阶变结构等效电路模型,包括永磁同步电机分数阶动态等效电路模型(以下简称动态等效电路模型)和考虑铁损的永磁同步电机稳态等效电路模型(以下简称稳态等效电路模型)两部分,其中,永磁同步电机分数阶动态等效电路模型主要用于电机响应速度控制等动态性能的研究,考虑铁损的永磁同步电机稳态等效电路模型主要用于电机效率优化等稳态性能的研究;两个模型之间通过切换控制实现在不同研究阶段中的模型变结构。
所述动态等效电路模型和稳态等效电路模型,均包括旋转坐标系下的d轴等效电路和q轴等效电路,两个等效电路均包括依次相连的电机对应轴电压ud或uq、电机定子绕组电阻rs、对应轴电流id或iq控制的电压源,其中,q轴等效电路还包括由转子永磁体的励磁磁通控制的电压源。此外,所述动态等效电路模型还包括电机对应轴分数阶电感ld或lq,所述分数阶电感的阶次基于最小二乘法辨识模型确定;所述动态等效电路模型还包括电机铁心损耗电阻rc;
进一步的,所述动态等效电路模型中的d轴等效电路,电路电压方程表示为
式中,ud为电机d轴电压;id、iq分别为电机d轴和q轴电流;lq分别为电机q轴分数阶电感大小;rs为电机定子绕组电阻;np为定子绕组的极对数;ωm为转子机械角速度。
进一步的,所述动态等效电路模型中的q轴等效电路,电路电压方程表示为
式中,uq分别为电机q轴电压;ψf为转子永磁体的励磁磁通。
进一步的,所述稳态等效电路模型中的d轴等效电路,电路电压方程表示为ud=rs(id+idc)-npωmlqiq=rs(id+idc)+rcidc,式中,idc为电机定子中铁心损耗电流的d轴电流分量,rc为电机铁心损耗电阻。
进一步的,所述稳态等效电路模型中的q轴等效电路,电路电压方程表示为uq=rs(iq+iqc)+npωmldid+npωmψf=rs(iq+iqc)+rciqc,式中,iqc为电机定子中铁心损耗电流的q轴电流分量。
所述动态等效电路模型的分数阶电感,利用分数阶微积分理论来描述实际电感特性的分数阶电感模型,其特性方程表示为
所述的分数阶电感的阻抗za(s),令s=jω,表示为:
所述考虑铁损的永磁同步电机分数阶变结构等效电路模型,其输出转矩表示为te=np[ψf+(ld-lq)id]iq,式中,te为电机的输出转矩。
一种应用上述考虑铁损的永磁同步电机分数阶变结构等效电路模型及其辨识方法,包括以下步骤:
步骤一:根据分数阶微积分理论,实际的电感模型是分数阶元件,分数阶电感的特性方程及传递函数可以表示为
式中:α为分数阶电感的分数阶阶次;i(t)和u(t)分别为分数阶电感通过的电流和两端电压;ua(s)、ia(s)分别表示分数阶电感电压和电流的象函数;za(s)为分数阶电感的阻抗,如果令s=jω,则可以表示为:
实际的永磁同步电机系统具有显著的电感特性,因此也是分数阶的物理系统,根据所述的动态等效电路模型,由电路电压方程和电机输出转矩方程,可得:
式中,ud、uq分别为电机d轴和q轴电压;id、iq分别为电机d轴和q轴电流;ld、lq分别为电机d轴和q轴电感;rs为电机定子绕组电阻;np为定子绕组的极对数;ωm为转子机械角速度;ψf为转子永磁体的励磁磁通。
步骤二:根据永磁同步电机分数阶等效电路模型及其系统关系表达式,模型需要辨识的参数主要包括电机定子绕组电阻rs,电机d轴和q轴分数阶电感的大小ld、lq,分数阶电感的分数阶阶次α,转子永磁体的励磁磁通ψf。
步骤三:电机定子绕组电阻rs通过用电桥测量三相电阻可得到,一般永磁同步电机的三相定子绕组采用y型接法,通过3次测量的数据r1,r2,r3,电机定子绕组电阻rs=(r1+r2+r3)/6。
步骤四:电机的反电动势以a相相电压ea为例,其表达式为:ea≈npωmψf=2πf,而线电压uab为√3倍的相电压ea,因此可得磁链系数:
步骤五:当不考虑铁损时,电机稳态电压方程:
通过电压、电流及转速数据的采集,通过稳态计算可实现电机d轴和q轴分数阶电感ld、lq参数的离线辨识。
步骤六:根据
步骤七:采用一般的直接测试法,利用原动机与被测试电机对拖,利用不同负载下的测试计算电机铁心损耗,进而拟合得到电机铁心损耗电阻rc的变化曲线。
步骤八:通过以上实验和参数辨识,可以得到考虑铁损的永磁同步电机分数阶变结构等效电路模型,包括永磁同步电机分数阶动态等效电路模型和考虑铁损的永磁同步电机稳态等效电路模型两部分,两个模型之间通过切换控制实现在不同研究阶段中的模型变结构。
以上所述仅为本申请的优选实施例而已,并不用于限制本申请,对于本领域的技术人员来说,本申请可以有各种更改和变化。凡在本申请的精神和原则之内,所作的任何修改、等同替换、改进等,均应包含在本申请的保护范围之内。
上述虽然结合附图对本发明的具体实施方式进行了描述,但并非对本发明保护范围的限制,所属领域技术人员应该明白,在本发明的技术方案的基础上,本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。
- 还没有人留言评论。精彩留言会获得点赞!