带偏磁控制的精简矩阵变换器模型预测控制方法与流程

本发明属于电力电子技术领域，具体涉及一种带偏磁控制的精简矩阵变换器模型预测控制方法。

背景技术：

精简矩阵变换器(reducedmatrixconverter，rmc)是一种新型功率变换器，rmc拓扑如图1所示，它是由输入滤波器、rmc整流级、高频变压器、可控整流桥构成。rmc整流级完成了电网三相交流电压到正负交变的高频脉冲电压的转换，实现了三相到单相交-交变换，前级正负脉冲电压经高频变压器耦合到后级经整流成直流。与传统ac/dc-dc/ac-ac/dc三级变换器相比，rmc省去了中间dc/ac环节，简化了硬件电路，提高了转换效率。rmc还具有如下性能：1)输入电流正弦，可实现输入单位功率因数；2)具备能量双向流动功能，能够实现四象限运行；3)前后级通过变压器隔离，便于系统集成；4)直流侧无需储能电容，体积小，结构简单紧凑。

但是，rmc传统调制策略为近似开环控制，供电电源扰动会传到负载侧，负载扰动会影响输入性能。而模型预测控制以输入和输出性能为约束，能消除输入和输出扰动影响，始终获得优良输入输出性能。但模型预测控制缺陷之一是开关频率不固定，此策略控制下rmc变压器器因随机开关频率而存在偏磁饱和问题。

技术实现要素：

本发明的目的在于提供一种带偏磁控制的精简矩阵变换器模型预测控制方法，不仅能提高精简矩阵变换器的抗扰性，而且能解决变压器偏磁问题。

本发明所采用的技术方案是：带偏磁控制的精简矩阵变换器模型预测控制方法，以输入滤波器、精简矩阵变换器前级变换器、变压器、后级可控整流桥以及负载模型为基础，采样网侧输入电压、电流、精简矩阵变换器整流级输入侧电压和输出电流，构建精简矩阵变换器系统数学模型并离散化，以输入无功和输出电流误差为目标函数，寻出最优开关状态，采用正负脉冲交替分配模式解决变压器偏磁问题，实现精简矩阵变换器带偏磁抑制的模型预测控制

本发明的特点还在于，

具体按照以下步骤实施：

步骤1：建立精简矩阵变换器前后级开关数学模型；

步骤2：建立精简矩阵变换器前后级所有开关状态表；

步骤3：在步骤1的基础上，离散化精简矩阵变换器数学模型；

步骤4：在步骤1至步骤3的基础上，建立以输入无功功率和输出电流误差为目标函数的品质函数；

步骤5：在步骤1至步骤4的基础上，考虑变压器偏磁的脉冲序列分配：采用正负脉冲交替分配模式，解决传统模型预测控制随机开关状态导致的变压器偏磁问题。

步骤1具体为：

精简矩阵变换器前级变换器数学模型描述了精简矩阵变换器输入侧电压电流ue，ie与直流侧电压电流udc，idc的关系，其开关矩阵模型如下：

其中，sap、san、sbp、sbn、scp、scn均为精简矩阵变换器整流级开关；

后级可控整流桥的开关数学模型如下：

u0＝u1(s1-s3)(3)

i0＝i1(s1-s3)(4)

其中，u0和i0为输出电压和电流，u1和i1为变压器副边电压和电流，s1、s3均为后级可控整流桥的开关状态。

步骤2具体为：根据精简矩阵变换器整流级输出侧不能短路，输入侧不能开路的原则，精简矩阵变换器整流级三相桥臂共有九种开关状态组合，为了增大电压传输比，去除三种零矢量，只考虑有效矢量，如表1所示中的六种开关状态：

表1：

表1中，1表示开通，0表示关断；

后级可控整流桥列出了后级全桥整流的两种开关状态，如表2所示：

表2：

表2中，s1、s2、s3、s4均为后级可控整流桥开关，1表示开通，0表示关断。

步骤3具体为：

网侧相电流和精简矩阵变换器整流级输入侧相电压的离散化形式为：

其中，和分别表示第k时刻和k+1时刻整流级输入侧相电压值，和分别表示第k时刻和k+1时刻网侧相电流值，表示第k时刻整流级输入侧相电流值，表示第k时刻网侧相电压值；cf、lf和rf分别表示输入滤波器的容值、感值和等效电阻阻值，ts为开关周期；c和d为网侧相电压和rmc整流级输入侧相电压离散形式的系数矩阵；a和b为输入滤波参数组成的因子矩阵；系数矩阵中cij、dij用于计算一个采样周期后离散系统对应的变量的预测值(i＝1，2；j＝1，2)；i2*2为两行两列的单位矩阵；

负载模型的离散化表达式为：

其中，和分别表示第k时刻和k+1时刻系统输出电流值，表示第k时刻系统输出电压值，l1和r1表示负载的感值和阻值。

步骤4具体为：

输出电流预测参考值的误差表达式如下：

其中，上标“*”代表参考值，为k+1时刻预测电流；

网侧瞬时无功功率与其参考值的误差表达式如下：

其中，0是瞬时无功功率参考值，和分别为采样输入三相电压、电流经输入侧离散化模型预测所得两相静止坐标系下k+1时刻输入电压、电流的实部和虚部；

综合式(7)和式(8)，得到品质函数的表达式如下：

其中，λ为权重因子。

步骤5中考虑变压器偏磁的脉冲序列分配的具体过程是：每个开关周期分成两个相等的半周期，前半个开关周期时，精简矩阵变换器前级变换器为模型预测控制选择的开关状态矢量，后半个开关周期时，控制矢量为前半个周期方向相反的矢量，即前后半个周期状态下同一桥臂导通开关上下桥臂互换，使得每一个开关周期内精简矩阵变换器整流级的输出电压由两部分组成，两部分电压幅值相等方向相反，从而确保高频变压器原边电压始终为正负交变脉冲，解决变压器偏磁问题。

本发明的有益效果是：

1、本发明提供一种精简矩阵变换器模型预测控制方法，实现rmc模型预测控制，使rmc即使在电源和负载扰动条件下仍能获得控制目标性能(输入单位功率因数，输出电流高精度跟随)，提高rmc抗扰性。

2、本发明提供了一种模型预测控制下rmc变压器偏磁解决方法，相比于传统解决偏磁的方法，本发明不需要检测直流分量，无需增加硬件电路情况下，仅通过调整脉冲序列，利用算法就能完全消除模型预测控制下rmc变压器偏磁问题。

附图说明

图1是精简矩阵变换器的拓扑结构图；

图2是本发明带偏磁控制的精简矩阵变换器模型预测控制方法的实现框图；

图3是本发明带偏磁控制的精简矩阵变换器模型预测控制方法的流程图；

图4是本发明建立数学模型时输入滤波电路结构图；

图5是本发明建立数学模型时rmc整流级电路结构图；

图6是本发明建立数学模型时高频变压器电路结构图；

图7是本发明建立数学模型时可控整流桥电路结构图；

图8是本发明建立数学模型时负载电路结构图；

图9是本发明偏磁控制时整流级输出电压导通顺序图；

图10是本发明偏磁控制时前半周期电流流向；

图11是本发明偏磁控制时后半周期电流流向；

图12是本发明网侧输入电压电流仿真波形；

图13是本发明输出电流仿真波形；

图14是本发明加入偏磁控制变压器原边电流仿真波形；

图15是本发明加入偏磁控制变压器原边电流局部放大仿真波形；

图16是本发明未加入偏磁控制变压器原边电流仿真波形；

图17是本发明未加入偏磁控制变压器原边电流局部放大仿真波形；

图18是本发明输入电压瞬间跌落波形；

图19是本发明输入电压瞬间跌落时输入电流波形；

图20是本发明输入电压瞬间跌落时a相电压电流波形；

图21是本发明输入电压瞬间跌落时输出电流波形；

图22是本发明输入电压不平衡波形；

图23是本发明输入电压不平衡时输入电流波形；

图24是本发明输入电压不平衡时a相电压电流波形；

图25是本发明输入电压不平衡时输出电流波形。

具体实施方式

下面结合附图以及具体实施方式对本发明进行详细说明。

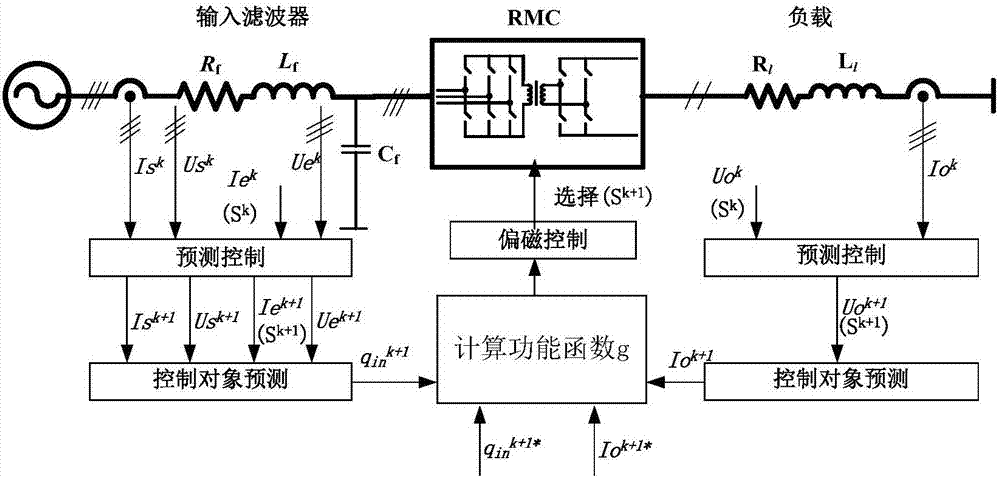
本发明提供了一种带偏磁控制的精简矩阵变换器模型预测控制方法，利用网侧输入电压(图4中usa、usb、usc)、电流(图4中isa、isb、isc)、rmc整流级输入侧电压(图5中uea、ueb、uec)、变压器原副边电压电流(图6中udc、idc、u1、i1)、输出电压电流(图8中u0、i0)及精简矩阵变换器开关矩阵模型，建立精简矩阵变换器数学模型并离散化，根据建立的离散化数学模型对输入无功功率和输出电流进行预测，并建立下一时刻输入无功功率和输出电流与各自参考值之间误差的品质函数，以此品质函数为约束对精简矩阵变换器的开关状态进行寻优，利用最优开关状态实现精简矩阵变换器的输出跟随。模型预测控制的实现框图如图2所示。

a.数学模型的建立

rmc的拓扑如图1所示，表3给出了abc/αβ坐标系下rmc系统中电压电流表示符号。

表3abc/αβ坐标系下rmc电压电流表示符号

假定rmc网侧输入三相电压及所带负载对称，则任一变量x在αβ坐标系和abc坐标系下分别为：

整流级数学模型描述了rmc输入侧电压电流ue，ie与直流侧电压电流udc，idc的关系，其开关矩阵模型如下：

其中，sap、san、sbp、sbn、scp、scn均为精简矩阵变换器整流级开关，1表示开通，0表示关断。

输入滤波器的数学模型如下：

后级可控整流桥的开关数学模型如下：

u0＝u1(s1-s3)(3)

i0＝i1(s1-s3)(4)

其中，u0和i0为输出电压和电流，，u1和i1为变压器副边电压和电流，s1、s2、s3、s4均为后级可控整流桥的开关状态，1表示开通，0表示关断；

类似的，可以得到负载的数学模型如下：

b.建立开关状态表

根据精简矩阵变换器整流级输出侧不能短路，输入侧不能开路的原则，rmc整流级三相桥臂共有九种开关状态组合，为了增大电压传输比，在此将三种零矢量去除，只考虑有效矢量，如表1所示中的六种开关状态。类似的可控整流桥列出了后级全桥整流的两种开关状态，如表2所示。

表1整流级开关状态

表2全桥整流开光状态表

c.预测值计算

将上述建立的系统数学模型进行离散化。

网侧相电流和rmc整流级输入侧相电压预测值的计算公式可以由输入滤波器数学模型经离散化得到：

其中，系数cij、dij用于计算一个采样周期后离散系统对应的变量的预测值。cij、dij的具体计算结果可由输入滤波器数学模型的状态空间表达式得到。

其离散形式可以表示式(5)所示，

其中，

其中，和分别表示第k时刻和k+1时刻整流级输入侧相电压值，和分别表示第k时刻和k+1时刻网侧相电流值，表示第k时刻整流级输入侧相电流值，表示第k时刻网侧相电压值，cf、lf和rf分别表示输入滤波器的容值、感值和等效电阻阻值，ts为开关周期，a和b为输入滤波参数组成的因子矩阵，i2*2为两行两列的单位矩阵。

类似的，负载模型的离散化形式如(6)所示，

其中，和分别表示第k时刻和k+1时刻系统输出电流值，表示第k时刻系统输出电压值，l1和r1表示负载的感值和阻值。

d.品质函数

在预测控制策略中，不同的品质函数具有不同的控制效果。

输出电流预测参考值的误差表达式如下：

其中，上标“*”代表参考值，为k+1时刻输出电流。

网侧瞬时无功功率与其参考值的误差表达式如下：

其中，0是瞬时无功功率参考值，和分别为k+1时刻静止坐标系下网侧输入电压、电流的实部和虚部，为采样输入三相电压、电流经输入侧离散化模型预测所得两相静止坐标系下k+1时刻输入电压、电流；

综合式上述两式，可以得到品质函数的表达式如下：

其中，λ为权重因子。

e.考虑偏磁的脉冲分配

如图9所示，将每个开关周期分成两个相等的半周期，前半个开关周期时，rmc前级变换器为模型预测控制选择的开关状态矢量，如图10所示，假设为开通sbp和san；后半个开关周期时，如图11所示开通sbn和sap，控制矢量为前半个周期方向相反的矢量，即前后半个周期状态下同一桥臂导通开关上下桥臂互换，使得每一个开关周期内rmc整流级的输出电压由两部分组成，两部分电压幅值相等方向相反。从而确保高频变压器原边电压始终为正负交变脉冲，解决变压器偏磁问题。

仿真验证：

为了验证本发明带偏磁控制的精简矩阵变换器模型预测控制方法的有效性，在matlab/simulink环境下进行了仿真，仿真总时间为0.4s，在0.2s时输出电流给定由25a突增到50a，仿真参数如下表：

表4仿真参数

仿真结果如图12-图15所示。

图12为该控制方法下rmc输入相电压和输入相电流波形，由波形知，输入电压电流同相位，实现了网侧单位功率因数，在0.2s突加负载时电流正弦度仍较好，验证了本发明带偏磁控制的精简矩阵变换器模型预测控制下rmc具有良好的输入性能。

图13为该控制方法下rmc输出电流波形，从图中可以看出，输出电流跟随给定值，并且在负载突加时也能较快跟随给定值，并能稳定运行，验证了本发明带偏磁控制的精简矩阵变换器模型预测控制下系统具有良好的输出跟随和抗负载扰动性能。

图14和图15分别为传统mpc下rmc变压器电压波形和局部放大波形，由波形知，不带变压器直流偏磁抑制的mpc将会导致变压器原边电压正负不对称，从而会导致变压器偏磁问题。

图16为带偏磁抑制的模型预测控制下rmc变压器原边电压波形，图17为变压器原边电压局部放大(将0.15s—0.152s波形放大)，从图17中可以看出，变压器原边电压正负交变，变压器不存在偏磁问题，并且在0.2s负载突加时能够很好的响应输出电流变化，验证了本发明带偏磁控制的精简矩阵变换器模型预测控制解决偏磁问题方法的有效性。

图18为设置三相输入电压在0.1s时下降50％来模拟电压跌落；图19为输入电压跌落时三相输入电流波形，输入电流仍为正弦波；图20为输入电压跌落前后a相电压电流波形，在电压跌落前后网侧都能保持单位功率因数；图21为输入电压跌落前后输出电流波形，从图中可以看出，输入电压跌落前后输出电流仍能较好跟随参考，从而表明所发明控制方法使系统具有较强抵御电网跌落扰动特性。

在电网不平衡工况对所发明方法进行测试，图22为三相不平衡输入电压波形，其中a相电压不平衡，b相相位不平衡(us＝[150sin(100πt)311sin(100πt-90°)311sin(100πt+120°)])；图23为三相输入不平衡时输入电流波形，可以看出输入电流仍为正弦波；图24为输入不平衡时a相电压电流波形，输入仍然保持单位功率因数；图25为输出电流和参考电流波形，由波形知即使在三相输入不平衡工况下，输出电流仍保持高度跟随参考，从而验证了所发明控制方法下系统具有较强的电网不平衡抗扰能力。

由输入电压瞬时跌落和三相输入电压不平衡工况测试波形知，本发明带偏磁控制的精简矩阵变换器模型预测控制对非正常输入(跌落和不平衡)具有较强的抵御能力，从而使系统具有较强的抗扰特性。