本发明涉及高频响永磁同步直线伺服系统的技术领域,尤其涉及一种永磁同步直线伺服系统速度环pi-ip控制参数自校正方法。
背景技术
永磁同步直线伺服系统结构简单,不需要中间传动环节就能直接实现直线运动,具有相对小的负载惯量及高动态响应的优点,广泛应用于数控机床、半导体芯片制造及精密仪器等领域。永磁同步直线伺服系统的控制性能不仅取决于其硬件制造水平,而且决定于直线伺服驱动中所采用的控制策略和设置的控制参数。只有当直线伺服驱动采用的控制策略、设置的控制参数和永磁同步直线伺服系统自身固有特性之间形成良好匹配时,永磁同步直线伺服系统才能处于最优工作状态。
在永磁同步直线电机运行过程中,速度指令可能需要做出调整,针对这样的调整,直线伺服驱动需要具备良好的瞬态响应跟踪。当速度指令恒定时,针对不同的运行工况,直线伺服驱动需要具备较强的抗扰动能力。这样直线伺服驱动使用pi或ip控制器很难同时满足瞬态响应和抗扰动能力的要求。大量研究表明,pi-ip控制器综合了pi和ip控制器的优缺点,能够在不影响永磁同步直线伺服系统闭环稳定性的基础上,有效地提高永磁同步直线伺服系统的动态性能。但是pi-ip控制器存在更多的控制参数需要实时调整,为了满足永磁同步直线伺服系统高速高精的发展趋势,需要探求一种高效的永磁同步直线伺服系统速度环pi-ip控制器的参数自校正方法和途径。
一般而言,可将控制器参数自校正方法分为以下两类:一类是基于规则的自校正方法,如模糊pid,神经网络等,文献(a.rohan,f.asghar,s.h.kim,designoffuzzylogictunedpidcontrollerforelectricvehiclebasedonipmsmusingflux-weakening[j],journalofelectricalengineeringandtechnology,2018,13(1):451-459提出一种随机模糊pid的自校正方法。这类算法的计算量较大,不能满足伺服系统实时性需求,同时不恰当的控制参数初始值会使得在线校正过程陷入局部最优,无法保证最优的实时控制效果。另一类是基于模型的自校正方法,文献(yasukikansha,lijia,min-senchiu.self-tuningpidcontrollersbasedonthelyapunovapproach[j].chemicalengineeringscience,2008,63(10):2732-2740)提出一种基于模型的pid控制参数自校正方法。基于模型的自校正方法算法简单,稳定性好,但是依赖被控模型结构和参数的辨识精度。鉴于上述两类自校正方法的优缺点,本发明拟采用改进的递推经验频率参数估计法对速度环被控模型参数进行在线高精辨识,同时提出一种李雅普诺夫控制方法来实现速度环pi-ip控制器的参数自动校正。
技术实现要素:
本发明要解决的技术问题在于针对现有技术中的缺陷,提供一种永磁同步直线伺服系统速度环pi-ip控制参数自校正方法,该控制方法能适应永磁同步直线电机高频响特性,快速跟踪系统指令,也能适应具有负载质量、负载力等非线性特点的高速高精应用场合。
本发明解决其技术问题所采用的技术方案是:
本发明提供一种永磁同步直线伺服系统速度环pi-ip控制参数自校正方法,通过在永磁同步直线伺服系统中采用pi-ip控制器,并实时自动校正pi-ip控制器的参数,实现对永磁同步直线伺服系统的高性能速度控制,该方法包括以下步骤:
s1、提取永磁同步直线伺服系统的推力电流指令与直线速度反馈,建立速度环被控模型,并实时辨识速度环被控模型参数;
s2、基于速度环被控模型,预测k+j时刻永磁同步直线伺服系统的速度输出;建立李雅普诺夫评价指标,判断速度跟踪性能;
s3、简化李雅普诺夫评价指标增量函数,在稳定条件下得到pi-ip控制器的参数在线优化结果,实现速度环pi-ip控制器的控制参数自校正。
进一步地,本发明的该方法中实时辨识速度环被控模型参数的方法为:
永磁同步直线伺服系统中,速度环被控模型的参数通过改进的递推经验频率参数估计法来在线辨识,其中,速度环被控对象模型的离散表达式为:
其中,a1、a2和b1是要辨识的模型参数,ωf为直线速度反馈,为推力电流指令;
其在线辨识过程可以通过如下方程组来进行:
h(k)=h(k-1)-m-1(k)h(k-1)
×[φ(k)βt(k)φ(k-1)
+φ(k-1)tβ(k)ψt(k)]h(k-1)
+l-1(k)m-1(k)h(k-1)
×[ψ(k)h(k-1)ψt(k)φt(k-1)β(k)
×βt(k)φ(k-1)-σ(k)ψ(k)ψt(k)]h(k-1)
其中,k为采样时刻,为待辨识的模型参数向量,为输入输出数据向量,h(k)为二次递推矩阵,其余中间变量如下:
φ(k)=[ψ(k-1),ψ(k)]t
y(k)=[ωf(k-1),ωf(k)]t
β(k)=[1,1]t×[x(k)x(k-1)+x(k-1)x(k-2)+x(k)x(k-2)]
σ(k)=x*(k)-βt(k)φ(k-1)h(k-1)φt(k-1)β(k)
l(k)=1+ψt(k)h(k-1)φt(k-1)β(k)
m(k)=l(k)+l-1(k)σ(k)ψt(k)h(k-1)ψ(k)
x*(k)=x2(k)+x2(k-1)+x2(k-2)
其中,φ(k)为输入输出历史与当前数据,y(k)为输出历史与当前数据,β(k)为加权向量,σ(k)、l(k)、m(k)和x*(k)均为参与递推运算的中间变量。
进一步地,本发明的该方法中采用李雅普诺夫来实现pi-ip控制器的参数最优校正,其具体步骤如下:
(1)预测输出:结合永磁同步直线伺服系统速度环被控模型参数,预测k+1时刻系统的速度输出,得到预测速度误差,其推导过程如下:
e(k+1)=ωr(k+1)-ωf(k+1)
其中,ωr(k)为直线速度指令,为预测速度输出,ωf(k+1)为实际速度输出,er(k+1)为预测速度误差,e(k+1)为实际速度误差;
(2)建立李雅普诺夫评价指标:通过更新速度环pi-ip控制参数,使得速度预测输出和速度指令保持一致,其评价指标函数表示为:
其中,λ是一个正实数;
(3)pi-ip控制参数在线自校正:永磁同步直线伺服系统的加速度定义为α,优化李雅普诺夫评价指标增量函数,得到pi-ip控制参数在线学习过程;
其中,ψ(k+j)=[ψ1(k+j),ψ2(k+j),ψ3(k+j)]t,ωf(k)为其余中间变量如下:
eu(k)=[e(k),δωr(k),-δωf(k)]
进一步地,本发明的该方法中pi-ip控制参数在线校正结果通过如下公式计算得到:
进一步地,本发明的该方法中的pi-ip控制器表达为以下增量模式:
其中,kv,ki和kα为pi-ip控制器的控制参数且kα∈[0,1];当kα=1,pi-ip控制器退化为pi控制器,当kα=0,pi-ip控制器退化为ip控制器。
本发明产生的有益效果是:本发明的永磁同步直线伺服系统速度环pi-ip控制参数自校正方法,1、在被控对象模型结构已知的情况下,采用改进的递推经验频率参数估计法,直接根据当前和过去的输入输出数据估计被控模型动态参数,算法实时性强,辨识精度高。2、本发明进一步扩大李雅普诺夫方法的适用范围,针对pi-ip控制器独特的控制结构,在系统全局稳定情况下,李雅普诺夫法能有效地调整控制参数,同时也保持了pi和ip控制器的优良特性。3、本发明可满足高频响永磁同步直线伺服系统的指令快速调整,也能适应负载质量和负载力等非线性特性应用场合。工程人员不需要根据手动设定和调节控制参数,系统自动完成速度环pi-ip控制参数自校正。
附图说明
下面将结合附图及实施例对本发明作进一步说明,附图中:
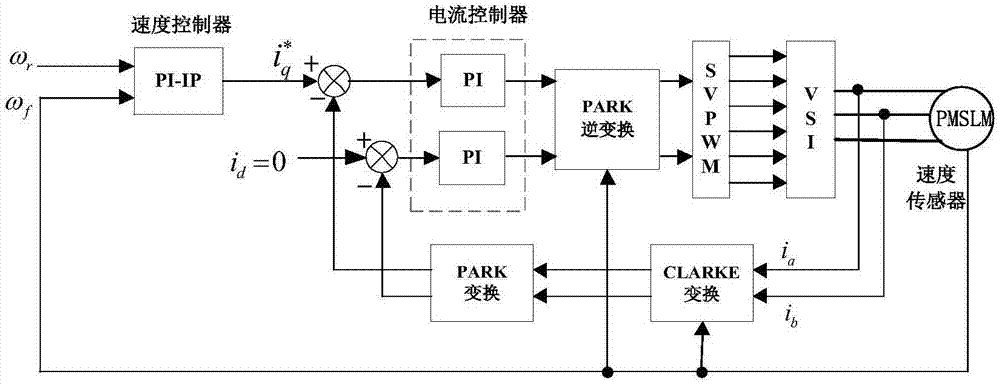
图1是本发明实施例的永磁同步直线伺服系统矢量控制结构示意图。
图2是本发明实施例的pi-ip控制器结构图。
图3是本发明实施例的控制参数自校正原理结构示意图。
图4是本发明实施例的控制参数自校正流程图。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合附图及实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅用以解释本发明,并不用于限定本发明。
图1为本发明永磁同步直线伺服系统矢量控制结构示意图。在实际工程应用中,通常采用id=0来实现电流的近似解耦。在图2中,通过对永磁同步直线伺服系统的速度环被控对象模型进行离散化处理,可以得到速度环被控对象的二阶离散模型:
其中,a1、a2和b1是需要辨识的模型参数,ωf为直线速度反馈,为推力电流指令。
其中,kv,ki和kα为pi-ip控制器的控制参数且kα∈[0,1]。当kα=1,pi-ip控制器退化为pi控制器,当kα=0,pi-ip控制器退化为ip控制器。e(k)=ωr(k)-ωf(k),ωr(k)为直线速度指令,e(k)为实际速度误差。
自校正方法采用李雅普诺夫控制方法,其基本原理如图3所示。在得到速度环被控模型参数后,对k+1时刻的速度输出进行预测,从而对系统预测输出误差进行在线评价,并根据评价结果推导出pi-ip控制参数的迭代公式,从而实现pi-ip控制参数的在线校正,满足永磁同步直线伺服系统瞬态响应和抗扰动能力的要求。
基于李雅普诺夫的永磁同步直线伺服速度环pi-ip控制参数的自校正流程图如图4所示,主要有以下几步:
第一步,首先需要实时提取永磁同步直线伺服速度环中的实际直线速度ωf和推力电流指令作为改进后的递推经验频率参数估计方法的输入输出数据。通过实时在线辨识得到所需的被控模型参数和改进后的递推经验频率参数估计方法如下:
h(k)=h(k-1)-m-1(k)h(k-1)
×[φ(k)βt(k)φ(k-1)
+φ(k-1)tβ(k)ψt(k)]h(k-1)
+l-1(k)m-1(k)h(k-1)
×[ψ(k)h(k-1)ψt(k)φt(k-1)β(k)
×βt(k)φ(k-1)-σ(k)ψ(k)ψt(k)]h(k-1)
其中,k为采样时刻,为待辨识的模型参数向量,为输入输出数据向量,h(k)为二次递推矩阵,其余中间变量如下:
φ(k)=[ψ(k-1),ψ(k)]t
y(k)=[ωf(k-1),ωf(k)]t
β(k)=[1,1]t×[x(k)x(k-1)+x(k-1)x(k-2)+x(k)x(k-2)]
σ(k)=x*(k)-βt(k)φ(k-1)h(k-1)φt(k-1)β(k)
l(k)=1+ψt(k)h(k-1)φt(k-1)β(k)
m(k)=l(k)+l-1(k)σ(k)ψt(k)h(k-1)ψ(k)
x*(k)=x2(k)+x2(k-1)+x2(k-2)
其中,其中,φ(k)为输入输出历史与当前数据,y(k)为输出历史与当前数据,β(k)为加权向量,σ(k)、l(k)、m(k)和x*(k)均为参与递推运算的中间变量,ωf为直线速度反馈,为推力电流指令。
第二步,结合速度环被控模型参数,预测k+1时刻系统的速度输出,判断速度是否跟踪良好,设其李雅普诺夫评价指标如下:
其中er(k+1)为预测速度误差,λ是一个正实数;
ωr(k+1)为设定速度;
为预测速度输出;
定义er(k+1)=er(k)+δer(k+1),李雅普诺夫评价指标增量函数δv(k)可通过如下方式获得:
第三步,当永磁同步直线电机以加速度α运行的时候,上式中的δer(k+1)可以表示为:
其中,上述式子中关键函数可表示如下:
在李雅普诺夫评价指标增量函数基础上,可得到全局收敛的pi-ip控制参数在线学习过程。
当调整参数ψ(k+1)满足上面的式子时,可以保证δv(k)在全局范围内总为负数,即表示速度的跟踪误差会趋近于零,系统是稳定的。得到pi-ip控制器的参数在线校正结果如下:
应当理解的是,对本领域普通技术人员来说,可以根据上述说明加以改进或变换,而所有这些改进和变换都应属于本发明所附权利要求的保护范围。