配电网中分布式储能的位置和容量优化配置方法与流程

本发明属于配电网分布式储能技术领域，尤其是一种配电网中分布式储能的位置和容量优化配置方法。

背景技术

当分布式储能接入配电网后，配电网潮流的方向和大小将发生改变，随之将对配电网的网损和电压产生影响。国内外学者从不同角度对分布式储能接入配电网的位置和容量优化配置方法进行了研究。例如，以储能安装成本、储能运行成本、切断可中断负荷的罚金及新电路的扩展成本的总和为目标函数，以配电网扩展规划为场景研究分布式储能的选点布局和容量配置。例如，提出了储能布局和尺寸的概念，证明了当发电成本曲线是凸的和递减的情况下，总是存在一个最优的容量分配方案。例如，提出了一种基于成本的方法来优化配电网中分布式储能的接入位置和容量。例如，研究了分布式储能和其他资源(如分布式电源和电容器)的规划问题，分布式储能被视为预留的调度资源。例如，考虑了分布式储能接入配电网的多目标优化问题，用智能优化算法对配电网中分布式储能的接入位置和容量进行优化。例如，对分布式电源和电动汽车充电桩的选址和定容进行了深入的讨论。例如，以电压灵敏度系数作为节点功率注入的函数来确定能够改善配电网电压水平的分布式储能接入位置。

综上所述，分布式储能在配电网中的应用已引起各方面的重视。目前对分布式储能的研究中，同时对分布式储能在配电网中的位置和容量优化配置方法的研究较少。且已有的研究对分布式储能的利用率较低，所采用的优化配置方法耗时长，不适用于大型系统。

技术实现要素：

本发明的目的在于克服现有技术的不足，提出一种配电网中分布式储能的位置和容量优化配置方法，其使用网损灵敏度公式计算配电网各节点24小时的网损灵敏度，并根据各节点网损灵敏度方差确定配电网中各节点接入分布式储能的优先顺序，精确找到了分布式储能的安装位置，有利于分布式储能容量的优化，且缩小了求解空间，计算效率高。另外，以配电网网损和节点电压波动为目标函数，采用基于模拟退火的粒子群优化算法对选定节点分布式储能的充放电功率进行优化，并由此确定分布式储能的最优接入容量。

本发明解决其技术问题是采取以下技术方案实现的：

一种配电网中分布式储能的位置和容量优化配置方法，包括以下步骤：

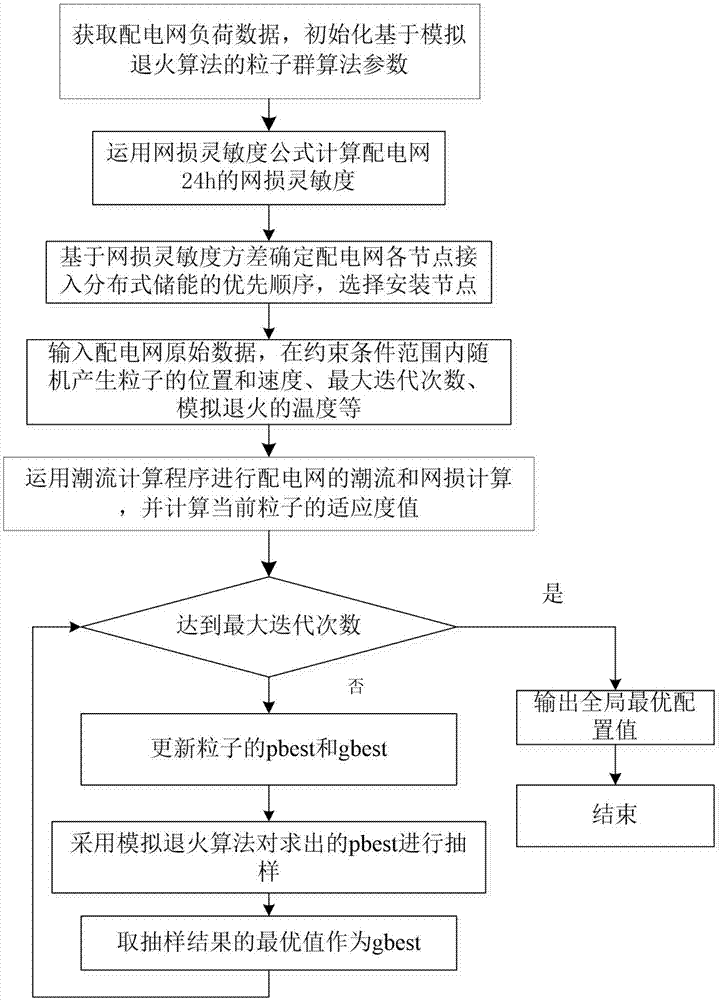
步骤1、获取配电网负荷数据，初始化基于模拟退火的粒子群算法的位置和速度、粒子种群大小、最大迭代次数、模拟退火的温度。

步骤2、设定分布式储能在配电网中的安装节点个数n；计算配电网各节点24h的网损灵敏度，并根据网损灵敏度画出配电网各节点的网损灵敏度曲线；

步骤3、综合考虑配电网各节点24h的网损灵敏度变化，计算配电网各节点的网损灵敏度方差，并确定配电网各节点接入分布式储能的优先顺序，选择安装节点；

步骤4、根据当前分布式储能的接入个数n，对分布式储能的位置和功率进行编码；

步骤5、根据粒子初始负荷节点的注入功率值，运用潮流计算程序进行配电网的潮流和网损计算，并根据分布式储能的容量优化模型计算当前粒子的适应度值；

步骤6、更新粒子的pbest和gbest值；

步骤7、采用模拟退火算法对求出的pbest进行抽样，产生新解并计算目标函数值，采用metropolis准则对最优解保留或者舍弃；

步骤8、根据抽样的结果得到全局最优解gbest，并检查是否达到最大迭代次数，若没有达到则转向步骤6，否则转向步骤9；

步骤9、输出分布式储能的最优充放电功率；

步骤10、根据分布式储能的优化充放电功率和充放电时段来计算配电网中分布式储能的最优配置容量。

进一步，所述步骤2中的网损灵敏度的计算方法如下：

步骤2.1、根据计算配电网网损；

其中，vi∠δi为节点i在t时刻的电压；vj∠δj为节点j在t时刻的电压；rij+jxij＝zij为节点阻抗矩阵的i行，j列元素；pi,pj分别为节点i,j在t时刻注入的有功功率；qi,qj分别为节点i,j在t时刻注入的无功功率；

步骤2.2、根据计算配电网24h的总网损；

步骤2.3、将ploss,t分别对pi,qi进行求导，得到配电网各节点的网损灵敏度公式：

进一步，所述步骤3中的网损灵敏度方差按如下公式计算：

δi为节点i在t时刻的网损灵敏度方差，δi综合考虑了分布式储能的充放电运行状态。

进一步，所述步骤4对分布式储能的位置和功率进行编码的形式如下：

x＝[x1,x2,…xn,y1,y2,…yn,…yj·n+i,…yt·n]

式中：xi为第i个分布式储能的接入位置，应对其取整；yj·n+i为(j+1)时刻第i个分布式储能的充放电功率。

进一步，所述步骤5中的分布式储能的容量优化模型如下：

式中，ploss为原始配电网1天中的网络损耗；v为原始配电网1天中各节点电压波动的总和；n为配电网的节点数；t为1天中所划分的总时段数；vi,t,vref分别为t时刻节点i的电压幅值和基准电压值；λ1和λ2为目标函数的权重系数，且λ1+λ2＝1。

进一步，在步骤7中，在粒子群优化算法中引入模拟退火的思想，其速度和位置更新速度如下：

进一步，所述充放电功率的约束条件包括：

⑴功率平衡约束：

分别为t时刻配电网根节点处的有功功率和无功功率；分别为t时刻节点i上分布式储能发出或吸收的有功功率和无功功率；分别为t时刻节点i的有功负荷和无功负荷；vi,t,vj,t分别为t时刻节点i和j的电压幅值；gij和bij为节点i和j之间的电导值和电纳值；δij,t为t时刻i,j两节点之间的相角差；

⑵分布式储能充放电功率约束：

其中，pdss_max,pdss_min为分布式储能功率的上限和下限；

⑶分布式储能能量平衡约束：

所述步骤10中，分布式储能的最优配置容量的计算方法如下：

其中，e为节点i处分布式储能的最优配置容量，1～m1,m2～m3,mj～mn为样本数据中需要连续充电或者连续放电的时段，分别为t时刻节点i上分布式储能发出或吸收的有功功率，δt为样本数据采样时间间隔，η为分布式储能的充放电效率；

其中，

本发明的优点和积极效果是：

1、本发明使用网损灵敏度公式计算配电网各节点24小时的网损灵敏度，并根据各节点网损灵敏度方差确定配电网中各节点接入分布式储能的优先顺序。通过该方法得到分布式储能的最优接入位置，能确保分布式储能接入配电网后系统的网损最小，精确找到了分布式储能的安装位置，有利于分布式储能容量的优化，且缩小了求解空间，计算效率高。

2、本发明以配电网网损和节点电压波动为目标函数，采用基于模拟退火的粒子群优化算法对选定节点分布式储能的充放电功率进行优化，并由此确定分布式储能的最优接入容量。分布式储能的安装在降低配电网网损的同时，也可降低节点电压波动，且采用基于模拟退火的粒子群优化算法有效避免了搜索过程陷入局部最优解。

附图说明

图1是本发明的处理流程图；

图2是一种配电网系统结构图；

图3是符合时序曲线图。

具体实施方式

以下结合附图对本发明实施例做进一步详述。

一种配电网中分布式储能的位置和容量优化配置方法，如图1所示，包括以下步骤：

步骤1、步骤1、获取配电网负荷数据，初始化基于模拟退火的粒子群算法的位置和速度、粒子种群大小、最大迭代次数、模拟退火的温度等。

步骤2、设定分布式储能在配电网中的安装节点个数n；计算配电网各节点24h的网损灵敏度，并根据网损灵敏度画出配电网各节点的网损灵敏度曲线。

在本步骤中，网损灵敏度的计算方法如下：

步骤2.1、在配电网中，根据计算配电网网损。

其中，vi∠δi为节点i在t时刻的电压；vj∠δj为节点j在t时刻的电压；rij+jxij＝zij为节点阻抗矩阵的i行，j列元素；pi,pj分别为节点i,j在t时刻注入的有功功率；qi,qj分别为节点i,j在t时刻注入的无功功率。

步骤2.2、根据计算配电网24h的总网损。

步骤2.3、将ploss,t分别对pi,qi进行求导，得到配电网各节点的网损灵敏度公式：

网损灵敏度反映出一定的系统运行方式下，节点i增加单位负荷功率引起的网损变化量。网损灵敏度越大，说明该节点对配电网网损的变化越敏感。在网损灵敏度较低时充电，可尽可能减小配电网网损的增加量，在网损灵敏度较高时进行放电可最大化降低配电网网损。

步骤3、综合考虑配电网各节点24h的网损灵敏度变化，计算配电网各节点的网损灵敏度方差，并确定配电网各节点接入分布式储能的优先顺序，选择安装节点。

在本步骤中，网损灵敏度方差按如下公式进行计算：

δi为节点i在t时刻的网损灵敏度方差。δi综合考虑了分布式储能的充放电运行状态。对于配电网每个节点，网损灵敏度方差越大，网损灵敏度的波动范围越大，整体上越有利于配电网网损的降低。对于配电网每个节点，网损灵敏度方差越大，网损灵敏度的波动范围越大，整体上越有利于配电网网损的降低。

步骤4、根据当前分布式储能的接入个数n，对分布式储能的位置和功率进行编码。

在本步骤中，需要对分布式储能的位置和功率进行编码，编码形式如下：

x＝[x1,x2,…xn,y1,y2,…yn,…yj·n+i,…yt·n]

式中：xi为第i个分布式储能的接入位置，应对其取整；yj·n+i为(j+1)时刻第i个分布式储能的充放电功率。

步骤5、根据粒子初始负荷节点的注入功率值，运用潮流计算程序进行配电网的潮流和网损计算，并根据分布式储能的容量优化模型计算当前粒子的适应度值。

本步骤中的分布式储能的容量优化模型为：

式中，ploss为原始配电网1天中的网络损耗；v为原始配电网1天中各节点电压波动的总和；n为配电网的节点数；t为1天中所划分的总时段数；vi,t,vref分别为t时刻节点i的电压幅值和基准电压值；λ1和λ2为目标函数的权重系数，且λ1+λ2＝1。

步骤6、更新粒子的pbest和gbest值。

步骤7、采用模拟退火算法对求出的pbest进行抽样，产生新解并计算目标函数值，采用metropolis准则对最优解保留或者舍弃；

在本步骤中，在粒子群优化算法中引入模拟退火的思想，利用退火算法在一定概率控制下暂时接受一些劣质解的特性改进标准的粒子群优化算法。速度和位置更新速度如下：

步骤8、根据抽样的结果得到全局最优解gbest，并检查是否达到最大迭代次数，若没有达到则转向步骤6，否则转向步骤9；

步骤9、输出分布式储能的最优充放电功率。

本发明在对分布式储能的位置和容量进行优化配置时，不仅需要考虑系统的运行约束，同时考虑分布式储能的充放电功率约束。充放电功率的约束条件包括：

(1)功率平衡约束。

分别为t时刻配电网根节点处的有功功率和无功功率；分别为t时刻节点i上分布式储能发出或吸收的有功功率和无功功率；分别为t时刻节点i的有功负荷和无功负荷；vi,t,vj,t分别为t时刻节点i和j的电压幅值；gij和bij为节点i和j之间的电导值和电纳值；δij,t为t时刻i,j两节点之间的相角差。

(2)分布式储能充放电功率约束

其中，pdss_max,pdss_min为分布式储能功率的上限和下限。

(3)分布式储能能量平衡约束

步骤10、根据分布式储能的优化充放电功率和充放电时段来计算配电网中分布式储能的最优配置容量。分布式储能的最优配置容量的计算方法如下：

其中，e为节点i处分布式储能的最优配置容量。1～m1,m2～m3,mj～mn为样本数据中需要连续充电或者连续放电的时段，分别为t时刻节点i上分布式储能发出或吸收的有功功率，δt为样本数据采样时间间隔，η为分布式储能的充放电效率。

其中，

下面以一个配电网系统为例进行说明，该配电网系统如图2所示。

采用ieee33节点进行仿真分析，系统总的有功负荷为3715kw，无功负荷为2300kvar，基准电压为12.66kv，节点电压允许范围为0.95～1.05pu。

分布式储能允许接入节点为2～33，设定分布式储能为单位功率因数，最大接入节点为4个，最大接入功率为200kw。其中，ηch＝0.9，ηdis＝0.9，t＝24。

权重因子体现了各目标函数所占的比重，其值对目标函数的优化效果产生影响。已有研究指出，通常情况下各目标取相同权重因子便可达到综合最优，故取λ1＝λ2＝0.5。

典型日负荷曲线如图3所示。

使用网损灵敏度公式计算ieee33节点配电网系统各节点24h的网损灵敏度，并根据网损灵敏度大小画出ieee33配电网的网损灵敏度曲线图。

网损灵敏度反映出一定的系统运行方式下，节点i增加单位负荷功率引起的网损变化量。网损灵敏度越大，说明该节点对配电网网损的变化越敏感。在网损灵敏度较低时充电，可尽可能减小配电网网损的增加量，在网损灵敏度较高时进行放电可最大化降低配电网网损。

根据网损灵敏度方差公式计算配电网各节点的网损灵敏度方差，如表1所示，

表133节点配电网各节点的网损灵敏度方差

网损灵敏度方差综合考虑了分布式储能的充放电运行状态。对于配电网每个节点，网损灵敏度方差越大，网损灵敏度的波动范围越大，整体上越有利于配电网网损的降低。在配电网中安装分布式储能时，可以通过各节点网损灵敏度方差的大小对配电网各节点进行排序，选择网损灵敏度方差较大的节点进行安装，使有功优化在计算时优先补偿降损效果最好的节点，缩小计算时间，提高模型的求解效率。

从表1可知，网损灵敏度方差最大的节点是33，网损灵敏度方差最小的节点是1。此外，节点17、18、32和33的网损灵敏度方差比其它节点的大。因此，在这些节点上安装分布式储能有利于降低配电网网损。

基于网损灵敏度方差分析的结果，选取待安装节点的集合为{17,18,32,33}。运用改进的粒子群优化算法进行分布式储能的容量优化配置，结果如表2所示。

表2基于灵敏度方差的分布式储能位置和容量优化

求解得出接入分布式储能的总容量为3.283mw·h。合理的对分布式储能的位置和容量进行优化，不但能够降低配电网网损，而且还可以降低配电网节点电压波动。接入分布式储能后，配电网网损由1992kw降低到1910kw，节点电压波动由190.255kv降低到176.281kv。此外，分布式储能的接入有效抑制了配电网负荷峰谷差，优化后降低幅度达到44.6％。

当不考虑安装分布式储能的网损灵敏度方差时，将节点2～33作为待选安装节点，运用改进的粒子群优化算法对分布式储能的位置和容量进行优化，结果如表3所示。

表3考虑所有可安装节点的分布式储能位置和容量优化

求解得出分布式储能的优化安装节点为8、14、15、31，接入总容量为3.549mw·h。

由表3可知,当考虑所有可安装节点时，配电网网损和负荷峰谷差均得到了一定程度的降低。配电网网损降低了79kw，负荷峰谷差降低幅度为38.1％。配电网的电压水平得到了提高，节点电压波动由190.255kv降低到179.153kv。

通过表2和表3的对比可发现，在配电网降损和降低节点电压波动方面，基于网损灵敏度方差的配置方案略优于搜索所有可安装节点的配置方案。但在降低配电网峰谷差方面，基于网损灵敏度方差的配置方法明显优于搜索所有可安装节点的配置方法。与搜索所有可安装节点的配置方法相比，采用基于网损灵敏度方差的配置方法进行分布式储能的位置和容量优化时，分布式储能的配置容量减少0.266mw·h，迭代200次，耗时节省1.03mim。基于网损灵敏度方差的方法确定了对配电网网损变化比较敏感的几个点，精确找到了分布式储能的安装位置，有利于分布式储能容量的优化，且缩小了求解空间，计算效率高。

需要强调的是，本发明所述的实施例是说明性的，而不是限定性的，因此本发明包括并不限于具体实施方式中所述的实施例，凡是由本领域技术人员根据本发明的技术方案得出的其他实施方式，同样属于本发明保护的范围。