一种考虑运行方式不确定性的多机电力系统水轮机调速器参数设计方法与流程

本发明属于电网安全
技术领域：
，涉及一种水轮机调速器参数设计方法，具体涉及一种考虑方式不确定性的多机电力系统水轮机调速器参数设计方法。
背景技术：
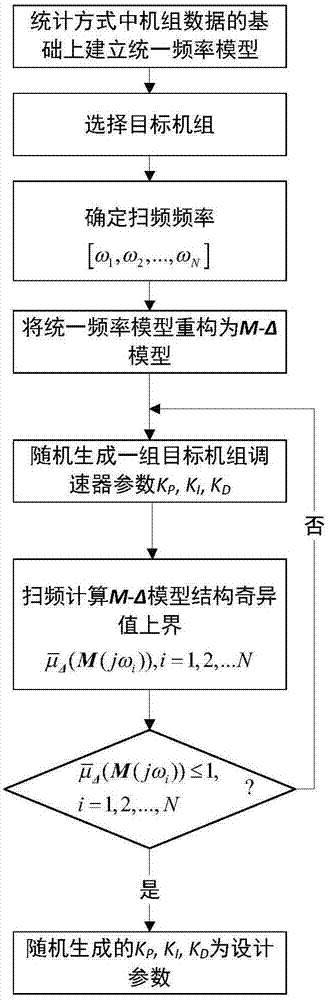
交流系统超低频振荡现象在国内外实际电网运行中均有发现，具有持续时间长、振荡频率极低(小于0.1hz)的特点，威胁系统安全稳定运行。自从云南电网与南方电网主网异步联网后，云南电网也出现了超低频振荡现象。已有研究对超低频振荡问题的机理做了较为深入的剖析，发现水电机组在超低频段内无法为系统提供足够的阻尼转矩，超低频振荡与系统中的水电机组一次调频关系密切。抑制超低频振荡最简单且有效的手段是切除水电机组调速器，然而切除调速器会降低机组跟踪负荷波动的性能，只能作为应急手段。调速器参数设计需综合考虑系统稳定性与跟踪性能，且应具有足够的鲁棒性应对运行方式变化导致的系统摄动。结构奇异值理论能够兼顾鲁棒稳定与鲁棒性能，是调速器控制参数设计的有力工具，且从未应用于解决超低频振荡问题。技术实现要素：本发明的目的是为了解决现有技术的不足，提供一种抑制超低频振荡问题的水轮机调速器参数设计方法，该方法兼顾了系统的稳定性要求与跟踪性能要求，且只要系统实际运行中由运行方式变化带来的摄动不超过预定值就能保证所设计的调速器参数有效性。为实现上述目的，本发明采用的技术方案如下：一种考虑运行方式不确定性的多机电力系统水轮机调速器参数设计方法，包括以下步骤：1)建立含有全系统主要发电机组在内的统一频率模型；2)选择调速器参数设计的目标电厂机组；3)确定扫频频率；4)将统一频率模型重构为m-δ模型；5)基于m-δ模型扫频设计调速器参数。进一步，优选的是，所述的步骤1)中的建立含有全系统主要发电机组的统一频率模型步骤：(1)统计全系统所含发电机组调速器和原动机模型的类型以及它们各自占全系统总容量的比例；(2)对超低频振荡发生时各电厂机组有功功率振幅从大到小排列，选择其中振幅最大的一个或几个电厂机组单独建模；对除单独建模的电厂机组外的剩余机组，将各类型调速器和原动机模型按照其各自占剩余机组有功出力总容量的比例从大到小排序，选择其中占比最大的1～4种模型搭建于统一频率模型中；(3)对于(2)中选定的调速器和原动机模型，将其参数设置为全系统中出力最大的该类型机组的参数；同时按照以下方式设置统一频率模型中各类型机组的台数：统计各类型机组在全系统中的总有功出力，则统一频率模型中各类型机组的台数等于其在全系统中的总有功出力除以它的单台有功出力；(4)根据全系统自动发电控制的安排设置统一频率模型中参与自动发电控制的机组台数：将统一频率模型中参与自动发电控制的机组台数设置为全系统中参与自动发电控制的机组总有功出力除以单台机组的有功出力的值。进一步，优选的是，所述的步骤2)中的选择调速器参数设计的目标电厂机组步骤：(1)计算所有单独建模电厂机组的阻尼系数md；对第i台机组，其阻尼系数mdi为：其中，re()为取实部运算，gti(s)为电厂机组调速器-原动机传递函数，s为拉普拉斯算子，j为虚数单位，ωc为振荡频率，单位为rad/s；(2)对于阻尼系数md从小到大排列，选择排列在第一个或前几个的电厂机组为调速器参数设计目标电厂机组。进一步，优选的是，所述的步骤3)中的确定扫频频率中，扫频频率[ω1,ω2,...,ωn]为一组数组，且需包含全系统发生超低频振荡时所有可能的振荡频率区间；其中ω1,ω2,...,ωn为扫频频率点，单位为rad/s。进一步，优选的是，所述的步骤4)中的将统一频率模型重构为m-δ模型步骤：假设编号为1～n的电厂机组为目标电厂机组；(1)在统一频率模型中，将除调速器参数设计的目标电厂机组外的系统统一为外部系统p(s)：其中：s为拉普拉斯算子，m∑为外部系统等效惯性常数，d为负荷阻尼系数，gti(s)为第i台电厂机组调速器-原动机传递函数；(2)统一频率模型中由运行方式不确定性带来的摄动如下：δ1,…,δn为电厂机组数目n1,…,nn的摄动，δp为外部系统的摄动；(3)在目标电厂机组总功率偏差∑δpm-∑δpe与目标电厂机组总负荷波动∑δpe之间插入用于表示性能的虚拟摄动δf，且δf的无穷范数|δf|∞<1；其中，∑δpm为目标电厂机组总有功功率波动；(4)设置摄动δ1,…,δn,δp和δf的权函数分别为w1,…,wn,wp(s)和ws(s)；其中：w1,…,wn和wp(s)应能够包络n1,…,nn和p(s)所有可能偏离标称情况的最大范围；ws(s)为性能权函数，表达式为：式中：s为拉普拉斯算子，m为灵敏度函数峰值上界，ωb*为带宽频率下界，a为最大稳态跟踪误差；(5)通过推导[u1,...,un,up,uf]t＝m·[v1,...,vn,vp,vf]t的关系得到m矩阵，从而将统一频率模型重构为具有对角结构型摄动δ＝diag{δ1,...,δn,δp,δf}的m-δ模型：式中其中：u1,…,un,up,uf为δ1,…,δn,δp和δf的输入信号，v1,…,vn,vp,vf为δ1,…,δn,δp和δf的输出信号，gti为目标电厂机组i的调速器-原动机传递函数，ni为目标电厂机组i数目的标称值，gtj为目标电厂机组j的调速器-原动机传递函数，nj为目标电厂机组j数目的标称值，p外部系统传递函数，wi,wp,wf分别为δi,δp,δf的权函数。进一步，优选的是，所述的步骤5)基于m-δ模型扫频设计调速器参数步骤：(1)对外部系统pk(s)扫频，设置每个扫频点处标称系统p(jωi)＝avg(pk(jωi))，权函数wp(jωi)＝max(|pk(jωi)-p(jωi)|)，其中：pk(jωi)为方式k的外部系统在扫频频率点ωi处的频率特性，j为虚数单位，ωi为扫频频率点，k为运行方式编号；(2)设置目标电厂机组数目的标称值和权函数；对目标电厂i，电厂机组数目的标称值ni＝(max(nik)+min(nik))/2，权函数wi＝(max(nik)-min(nik))/2，其中：nik为方式k中目标电厂i电厂机组数目，k为运行方式编号；(3)设置性能权函数ws(s)参数，带入并扫频得到每个扫频点处的ws(jωi)，其中：j为虚数单位，ωi为扫频频率点；s为拉普拉斯算子，m为灵敏度函数峰值上界，ωb*为带宽频率下界，a为最大稳态跟踪误差；(4)在各目标电厂机组调速器参数kp、ki、kd容许变化范围内，随机生成一组调速器参数kp、ki、kd；(5)将上述调速器参数带入各电厂机组调速器-原动机传递函数gt(s)，扫频得到每个扫频点处目标电厂机组调速器-原动机传递函数频率特性gt(jωi)，i＝1,2,…,n，其中：j为虚数单位，ωi为扫频频率点，i为扫频频率点序号；(6)在每个扫频点处将(1)～(5)中得到结果带入m-δ模型，计算系统结构奇异值上界其中，j为虚数单位，ωi为扫频频率点，i为扫频频率序号；(7)若以下条件满足其中，j为虚数单位，ωi为扫频频率点，i为扫频频率序号；则(4)中生成的kp、ki、kd满足要求，为最终的设计参数；否则返回(4)，重新生成一组调速器参数，并重复(5)～(6)，直至满足(7)所示的条件。本发明中，m为灵敏度函数峰值上界，是根据稳定要求设置；ωb*为带宽频率下界，是根据跟踪性能要求设置；a为最大稳态跟踪误差，设置为很小值，如0.0001。本发明与现有技术相比，其有益效果为：本发明基于结构奇异值理论，将运行方式不确定性处理为统一频率模型相应位置的摄动，且通过在功率偏差与负荷波动间插入虚拟摄动的方法将调速器设计需要考虑的鲁棒跟踪性能问题转化为鲁棒稳定问题。将摄动与系统分离，原系统被重构为包含对角型摄动的m-δ模型，从而设计过程为寻找使m-δ模型结构奇异值上界小于1的水轮机调速器参数。现有技术大部分只能针对单一工况设计单个调速器参数，无法应对多工况、多调速器参数整定问题。本发明可以同时设计多个调速器参数，且所设计的参数能够保证在所考虑的工况范围内系统性能均满足要求，解决了现有技术的不足。附图说明图1为本发明方法的流程示意图。图2为本发明方法中统一频率模型的示意图。图3为本发明实施例仿真验证中统一频率模型的示意图。图4为本发明实施例仿真验证中gs型调速器模型。图5为本发明实施例仿真验证中tb型汽轮机模型。图6为本发明实施例仿真验证中gh型机组模型。图7为本发明实施例仿真验证中gm型调速器模型。图8为本发明实施例仿真验证中ga型伺服器模型。图9为本发明实施例仿真验证中水轮机详细模型。图10为本发明实施例仿真验证中超低频段内目标机组gh原动机-调速器系统在s平面上的频域特性。图11为本发明实施例仿真验证中超低频段内目标机组gm原动机-调速器系统在s平面上的频域特性。图12为本发明实施例仿真验证中目标机组对应典型机组总出力变化后系统频率仿真曲线。具体实施方式下面结合实施例对本发明作进一步的详细描述。本领域技术人员将会理解，下列实施例仅用于说明本发明，而不应视为限定本发明的范围。实施例中未注明具体技术或条件者，按照本领域内的文献所描述的技术或条件或者按照产品说明书进行。所用材料或设备未注明生产厂商者，均为可以通过购买获得的常规产品。如图1所示，采用本发明方法进行处理时，通过建立含有全系统主要发电机组调速器和原动机模型的统一频率模型，可以实现对原全系统超低频振荡的模拟，避免了使用复杂的详细模型，减小了模型复杂度；通过确定包括振荡频率在内的扫频频率[ω1,ω2,...,ωn]，可以确定需要计算结构奇异值上界的频率点；基于建立的统一频率模型，可以将全系统重构为参数设计使用的m-δ模型；通过将统一频率模型重构为m-δ模型，并且随机生成一组目标机组调速器参数kp、ki、kd，扫频计算各扫频频率[ω1,ω2,...,ωn]处的结构奇异值上界若在各扫频频率[ω1,ω2,...,ωn]处结构奇异值上界则随机生成的目标机组调速器参数kp、ki、kd为最终的设计参数。本发明的具体实施例如下：(1)统计南方电网2017冬大、冬小、夏大、夏大极限、夏小、夏小外送、汛期方式中云南电网的机组数据和潮流计算结果的基础上，建立统一频率模型。按照之前所述步骤，在matlab/simulink软件中建立统一频率模型如图3所示。以冬大方式为例，上述的统一频率模型建立遵循如下步骤：1)方式数据中火电出力为3977.2mw，水电出力为32559mw。2)根据实际监测数据，电厂机组(nzd，ldl，xw，dcs)在振荡发生期间有功功率振幅从大到小排列排在最前，故单独建模，采用gm型调速器模块、ga型伺服器模块以及水轮机详细模型模块。对于火电机组，典型机组类型为gs(包含gs型调速器模块与tb型汽轮机模块)。对于水电机组，典型机组类型为gh(gh模型内本身包含调速器与原动机)和gm(包含gm型调速器模块、ga型伺服器模块以及水轮机详细模型模块)。单独建模电厂机组总出力为7885mw，gs型机组总出力为3977.2mw，gh型机组总出力为7717mw，gm型机组总出力为16957mw。3)对于2)中选定的调速器和原动机模型，将其参数设置为全系统中出力最大的该类型机组的参数，具体如下：对于单独建模电厂机组，nzd电厂机组功率基值为722.3mw，在其自身功率基值下机组惯性为10.38。其所含gm型调速器模型如图4所示，模式选择为开度模式、硬反馈输入信号为ypid，参数如表1。表1tr10.02td0.2kw2.9t10kp2t20kd1tr20.02ki0.37ep0.04其所含ga型伺服模型如图5所示，参数如表2。表2tc11.4kd0to18.5ki0t20.02td0kp10其所含水轮机详细模型如图6所示，图中水系统传递函数f(s)为其中，其中，tep为压力水管弹性时间常数，ts为调压室时间常数，twc为引水洞水击时间常数，twp为压力水管水击时间常数，zp为压力水管水阻抗，φc为引水洞摩擦系数，φp为压力水管摩擦系数，s为拉普拉斯算子。参数如表3。表3ldl电厂机组功率基值为400mw，在其自身功率基值下机组惯性为9.61。其所含gm型调速器模型如图4所示，模式选择为开度模式、硬反馈输入信号为ypid，参数如表4。表4tr10.02td0.198kw1.14t10kp2.5t20kd1tr20.02ki0.5ep0.04其所含ga型伺服模型如图5所示，参数如表5。表5tc9.35kd0to23ki0t20.2td0kp15其所含水轮机详细模型如图6所示，图中水系统传递函数f(s)为其中，其中，tep为压力水管弹性时间常数，ts为调压室时间常数，twc为引水洞水击时间常数，twp为压力水管水击时间常数，zp为压力水管水阻抗，φc为引水洞摩擦系数，φp为压力水管摩擦系数，s为拉普拉斯算子。参数如如表6。表6xw电厂机组功率基值为778mw，在其自身功率基值下机组惯性为8.72。其所含gm型调速器模型如图4所示，模式选择为开度模式、硬反馈输入信号为ypid，参数如表7。表7tr10.02td0.21kw1.35t10kp2t20kd1tr20.02ki0.375ep0.04其所含ga型伺服模型如图5所示，参数如表8。表8tc10kd0to13.1ki0t20.02td0kp6其所含水轮机详细模型如图6所示，图中水系统传递函数f(s)为其中，其中，tep为压力水管弹性时间常数，ts为调压室时间常数，twc为引水洞水击时间常数，twp为压力水管水击时间常数，zp为压力水管水阻抗，φc为引水洞摩擦系数，φp为压力水管摩擦系数，s为拉普拉斯算子。参数如表9。表9dcs电厂机组功率基值为250mw，在其自身功率基值下机组惯性为9.63。其所含gm型调速器模型如图4所示，模式选择为开度模式、硬反馈输入信号为ypid，参数如表10。表10tr10.2td0.3kw1.8t10kp4t20kd0tr20.02ki0.048ep0.04其所含ga型伺服模型如图5所示，参数如表11。表11tc21.5kd0to22.5ki0t20.2td0kp40其所含水轮机详细模型如图6所示，图中水系统传递函数f(s)为其中，其中，tep为压力水管弹性时间常数，ts为调压室时间常数，twc为引水洞水击时间常数，twp为压力水管水击时间常数，zp为压力水管水阻抗，φc为引水洞摩擦系数，φp为压力水管摩擦系数，s为拉普拉斯算子。参数如表12。表12对于典型机组gs，功率基值为353mw，在其自身功率基值下机组惯性为8.5。其所含gs型调速器模型如图7所示，tb型汽轮机模型如图8所示，参数如表13。表13k18.47trh8t10fip0.4t20tco0.4t30.5flp0.3tch0.3λ0fhp0.3对于典型机组gh，功率基值为109mw，在其自身功率基值下机组惯性为8.31。其所含gh型机组模型如图9所示，参数如表14。表14r0.04tw1tg0.25dd0.25tp0.04k’1td5对于典型机组gm，功率基值为667mw，在其自身功率基值下机组惯性为10.38。其所含gm型调速器模型如图4所示，模式选择为开度模式、硬反馈输入信号为ypid，参数如表15。表15tr10.2td0.21kw1.7t10kp2.5t20kd1tr20.02ki0.5ep0.04其所含ga型伺服模型如图5所示，参数如表16。表16tc13kd0to13ki0t20.2td0kp20其所含水轮机详细模型如图6所示，图中水系统传递函数f(s)为其中，其中，tep为压力水管弹性时间常数，ts为调压室时间常数，twc为引水洞水击时间常数，twp为压力水管水击时间常数，zp为压力水管水阻抗，φc为引水洞摩擦系数，φp为压力水管摩擦系数，s为拉普拉斯算子。参数如表17。表17冬大方式下，单独建模电厂(nzd，ldl，xw，dcs)机组台数分别为6,3,4,5台，总出力为7885mw。由于gs型典型机组出力为240mw，总出力为3977.2mw，因此gs型典型机组台数为3977.2/240≈17台。由于gh型典型机组出力为95mw，总出力为7717mw，因此gh型典型机组台数为7717/95≈81台。由于gm型典型机组出力为600mw，总出力为24842-7885＝16957mw，因此gm型典型机组台数为16957/600≈28台。4)agc增益kagc＝1。参与agc的机组类型为gh型和gm型，其台数ngh-agc为20台，ngm-agc为2台。故最终冬大方式统一频率模型中台数参数如表18。表18ngs17nagc-gh20ngh81nagc-gm2ngm28nnzd6nldl3nxw4ndcs5(2)计算单独建模电厂机组的阻尼系数md：nzd为-2.28，ldl为-1.08，xw为-1.40，dcs为2.45。选择阻尼系数md从小到大排列的前三个电厂机组(nzd，ldl，xw)作为调速器参数设计的目标机组。(3)由于对所有方式，全系统超低频振荡频率的范围为0.25～0.38rad/s，因此设定扫频频率范围为0.19～0.63rad/s。(4)将统一频率模型重构为如图10所示的m-δ模型。上述的重构遵循如下步骤，1)将除nzd、ldl、xw电厂机组外的系统统一为外部系统p(s)：其中：s为拉普拉斯算子，m∑为外部系统等效惯性常数，d为负荷阻尼系数。2)统一频率模型中由运行方式不确定性带来的摄动如下：δnzd、δldl、δxw为电厂机组数目nnzd、nldl、nxw的摄动，δp为外部系统的摄动；3)在目标电厂机组总功率偏差∑δpm-∑δpe与目标电厂机组总负荷波动∑δpe之间插入用于表示性能的虚拟摄动δf，且δf的无穷范数|δf|∞<1，以把鲁棒性能问题转化为鲁棒稳定问题；其中，∑δpm为目标电厂机组总有功功率波动；4)设置摄动δnzd、δldl、δxw、δp和δf的权函数wnzd、wldl、wxw、wp和ws。其中：wnzd、wldl、wxw、wp应能够包络nnzd、nldl、nxw和p可能偏离标称情况的最大范围；ws为性能权函数，表达式为式中：s为拉普拉斯算子，m为灵敏度函数峰值上界(根据稳定要求设置)，ωb*为带宽频率下界(根据跟踪性能要求设置)，a为最大稳态跟踪误差(设置为很小值，如0.0001)；5)通过推导[unzd,uldl,uxw,up,uf]t＝m·[vnzd,vldl,vxw,vp,vf]t的关系得到m矩阵，从而将全系统重构为具有对角结构型摄动δ＝diag{δnzd,δldl,δxw,δp,δf}的m-δ模型，其中：unzd,uldl,uxw,up,uf为δnzd、δldl、δxw、δp和δf的输入信号，vnzd,vldl,vxw,vp,vf为δnzd、δldl、δxw、δp和δf的输出信号。由图10易知以下关系成立推导得到如下m-δ模型其中(5)随机生成nzd、ldl、xw电厂机组水轮机调速器参数knzdp、knzdi、knzdd，kldlp、kldli、kldld，kxwp、kxwi、kxwd。其中各参数随机生成的范围为0<(knzdp,kldlp,kxwp)<10、0<(knzdi,kldli,kxwi)<0.5、0<(knzdd,kldld,kxwd)<3。(6)利用matlab的robustcontroltoolbox中的mussv()函数，扫频计算各扫频点处结构奇异值上界检验(5)中随机生成的参数是否满足要求。详细步骤如下：1)对所有七个方式外部系统pk(s)扫频，设置每个扫频点处标称系统p(jωi)＝avg(pk(jωi))，权函数wp(jωi)＝max(|pk(jωi)-p(jωi)|)，其中：j为虚数单位，ωi为扫频频率点，k为运行方式(冬大、冬小、夏大、夏大极限、夏小、夏小外送、汛期)。wp如图11所示；2)设置电厂机组的标称数目和权函数。由于在所有七个运行方式中，nzd电厂机组数目变化范围为2～5，ldl电厂机组数目变化范围为1～3，xw电厂机组数目变化范围为2～4，因此设置标称数目nnzd＝3.5，nldl＝2，nxw＝3，wnzd＝1.5，wldl＝1，wxw＝1；3)设置性能权函数ws(s)参数，带入并扫频得到每个扫频点处的ws(jωi)，其中：j为虚数单位，ωi为扫频频率点，s为拉普拉斯算子，m＝10，ωb*＝0.13，a＝0.0001；4)将随机生成的knzdp、knzdi、knzdd，kldlp、kldli、kldld，kxwp、kxwi、kxwd带入gtnzd,gtldl,gtxw,s为拉普拉斯算子。扫频得到每个频率点处的gtnzd(jωi),gtldl(jωi),gtxw(jωi)；5)在每个扫频点处，带入前述步骤计算得到的结果，得到每个扫频点处的m矩阵为一个数值矩阵，利用matlabrobustcontroltoolbox中的mussv()函数计算每个扫频点处的结构奇异值上界若满足如下条件则随机生成的knzdp、knzdi、knzdd，kldlp、kldli、kldld，kxwp、kxwi、kxwd为最终设计得到的调速器参数，否则回到步骤(5)重新随机生成一组调速器参数后重复上述步骤。最终设计得到的调速器参数如表19。表19knzdp0.87kldlp7.51kxwp0.95knzdi0.06kldli0.15kxwi0.14knzdd1kldld1kxwd1其结构奇异值上界如图12所示，可见原始参数不满足鲁棒性能，设计参数满足鲁棒性能。为了验证分析结果，计算了各方式全系统在原始参数和设计参数下的主导特征值与闭环带宽频率如表20。表20可见对于所有运行方式，设计参数在保证全系统闭环带宽(跟踪性能)的基础上大幅提高了主导模式的阻尼(稳定性)，从而说明了本发明方法的有效性。因此，本发明方法能够用于设计满足稳定性与跟踪性能要求的水轮机调速器参数，且所设计的参数有足够的鲁棒性应对方式不确定性，本发明方法具有突出显著的技术效果。以上显示和描述了本发明的基本原理、主要特征和本发明的优点。本行业的技术人员应该了解，本发明不受上述实施例的限制，上述实施例和说明书中描述的只是说明本发明的原理，在不脱离本发明精神和范围的前提下，本发明还会有各种变化和改进，这些变化和改进都落入要求保护的本发明范围内。本发明要求保护范围由所附的权利要求书及其等效物界定。当前第1页12