基于故障限流器的多馈入交直流输电系统的故障分区方法与流程

本发明涉及电力系统故障分析技术领域，特别是涉及基于故障限流技术的多馈入交直流输电系统的故障分区方法。

背景技术

在换流器中，退出导通的换流阀在反向电压作用的一段时间内如未能恢复阻断能力，或者在反向电压作用期间换相过程未进行完毕，则在阀电压变为正向时，被换相的阀将向原来预定退出导通的阀倒换相，这种情况称为换相失败。换相失败是直流系统最为常见的故障之一。而在多馈入交直流输电系统中，各逆变站间通过受端交流系统相互耦合，且电气距离较近，当某一系统发生故障时，可能引发各逆变站同时或相继换相失败。

多馈入交直流输电系统的同时换相失败问题目前并没有较好的解决办法。一般措施是改善直流系统的控制方式。一些学者提出柔性直流输电方式来克服换相失败问题。但这些方法只能减缓故障对每条直流换相失败的影响，而无法避免两条或多条直流系统同时发生换相失败。系统发生短路故障时，传统的做法是断路器动作，隔离故障，由此可能会导致负荷失去电源、电网解列，甚至系统失稳等严重后果。故障限流器可以在不改变电网结构以及系统运行方式下对短路电流进行限制，同时避免系统运行方式的改变带来交流系统的不稳定性。

故障限流器的工作原理为：系统正常运行时，限流器阻抗为零；短路故障发生时，线路电流迅速增大，安装在线路上的故障限流器的阻抗增大到一定值，从而限制短路电流的上升，起到隔离作用。故障消失后，故障限流器经过一段时间的延迟后阻抗恢复到零。

故障分区的基本思想就是利用故障限流器将直流多馈入受端系统划分为若干个相互之间由故障限流器隔开的同步运行区域，从而隔离故障，避免同时换相失败的发生。

技术实现要素：

本发明分析并推导了故障限流器对限制短路电流及补偿非故障处压降的作用，提出通过关联度法及非支配排序遗传算法(nsga-ii)相结合的算法来优化配置故障限流器从而实现非故障处的压降补偿，避免发生同时换相失败。

本发明提出的一种基于故障限流技术的多馈入交直流输电系统的故障分区方法，包括：

步骤1：建立故障限流器前后的等效电路，得出补偿压降；

步骤2：通过关联度法选取安装故障限流器的候选支路；

步骤3：采用nsga-ii对fcl即故障限流器进行优化配置，针对步骤1中得到的约束条件，确定fcl的最少安装数量；

步骤4：结合步骤2求得到候选支路与步骤3中的最少安装数量，形成故障分区，求取pareto最优解集x^*，即符合解空间内的非支配解的集合；

步骤5：当解集还包含其他解时，以投入经济性作为最优解的最后选取的标准。

进一步优选的技术方案，所述步骤1中建立故障限流器前后的等效电路，在节点i，j采用戴维南定理，得出的戴维南原理等效电路，其中xij,ij为等效电抗，则有，

其中，xij,ij为节点对(i,j)的自阻抗zij,ij的虚部值，ix为支路lij的短路电流，x为支路lij的电抗，

zij,ij＝zii+zjj-2zij(3)

则加入δx后，支路lij的短路电流为ix′

其中，u为支路lij开路时的电压，根据线性叠加原理，加入阻抗为δx的fcl后，相当于在支路lij注入δix的电流。

进一步优选的技术方案，所述步骤1中建立故障限流器前后的等效电路，根据叠加原理和节点对互阻抗的定义得出为注入电流δix后对节点p短路电流影响的等效电路，其中x0为节点p短路时的接地电阻，此时考虑最严重的金属短路情况：

δu'＝δix·xij,pq(7)

其中，xij,pq为节点对(i，j)对(p，q)的互阻抗zij,pq的电抗部分；

zij,pq＝zip+zjq-ziq-zjp(8)

将式(5)代入式(6)和(7)，并且令xm＝xij,ij+x，xm为总感抗，k＝u·xij,pq/xpq,pq，k为所设比值，所以可知

其中，短路电流为if，支路lij的电抗为x，流过支路lij的短路电流为ix，加入阻抗为δx的fcl后，支路lij的短路电流为ix-δix，短路电流为if-δif，xij,ij为节点p对(i,j)的自阻抗zij,ij的虚部值，u为支路lij开路时的电压，δu′为补偿压降，δif为电流变化量，xm＝xij,ij+x，k＝u·xij,pq/xpq,pq；

同样，非故障非安装fcl支路lmn的补偿电压δuy′也可以计算得到，表达式为

则当δx为0时，δu′或δuy′和δif两个变化量都为0，当δx从0开始增大时，两个变化量也随之增大，从而补偿线路短路造成的压降和抑制短路电流。

进一步优选的技术方案，所述步骤2中通过关联度法选取安装fcl的候选支路，选取支路阻抗为控制参数，推导得到短路点自阻抗对lij上fcl参数zfcl的关联度表达式如下：

其中，λ为关联度系数；p为故障发生点；zpi和zpj分别为节点i和j与故障点p之间的互阻抗；zp′为p点自阻抗；选取关联度更大的支路来配置fcl。

进一步优选的技术方案，所述步骤3中采用nsga-ii对fcl进行优化配置，确定fcl的最少安装数量，f1和f2表示约束条件1、2的值，具体目标函数和约束条件如下：

zfclmin≤zfcli≤zfclmin(i＝1,2，...，nfcl)(14)

δu-δu′≤0.2pu(15)

其中，nfcl为fcl的安装数量；δu为未发生故障的馈线出的未安装fcl时的压降，δu′为补偿压降，0.2pu是以未发生故障的馈线的原母线电压为标幺值。

进一步优选的技术方案，所述步骤4中先设ω表示问题的解空间，在式(16)当ω中不存在另一个解u使得fi(u)≤fi(x),i＝1,2,…,r时，称x∈ω是该问题的一个pareto非支配解，

其中，x为解向量；f(x)为目标函数向量；h(x)和g(x)分别为等式约束和不等式约束；

设x^*为一非支配解，若在整个可行域中没有任何解支配x^*，则x^*在pareto意义下是最优的，称为pareto最优解，则求出的pareto解的集合称为pareto最优解集，记为x^*。

进一步优选的技术方案，所述步骤5中以投入经济性作为最优解的最后选取的标准，根据实际经验，每套设备的安装及配套设施的成本是每单位欧姆的fcl成本的5至10倍，则选取成本最低的解作为最优解。

与现有技术相比，本发明的有益效果是：

通过推导故障限流器的限流电抗值与目标母线的短路电流限流量和非故障处压降补偿量的关系，证明了故障限流器对补偿非故障相压降从而避免其换相失败的作用。采用关联度法和非支配排序遗传算法(nsga-ii)进行多目标优化配置，实现了故障限流器的安装位置、数量和阻抗值的优化配置，从而实现了故障分区。最后，通过两条cigre推荐的直流单馈入标准模型结合ieee39节点电网仿真验证了所述方法的有效性和可靠性，大大减少了配置的搜索空间，提高了经济性，避免了多馈入交流输电系统的同时换相失败。

附图说明

构成本申请的一部分的说明书附图用来提供对本申请的进一步理解，本申请的示意性实施例及其说明用于解释本申请，并不构成对本申请的不当限定。

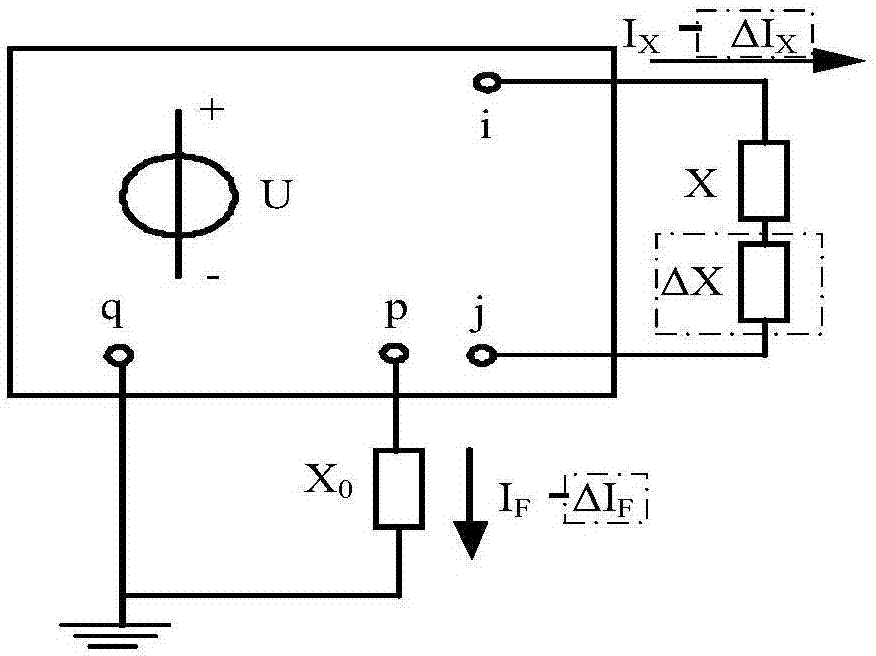
图1为故障限流器前后的等效电路图；

图2为戴维南定理等效电路图；

图3为叠加原理等效电路图；

图4为39节点交流电网图；

图5为最优解集图；

图6为pscad建立的模型图。

具体实施方式

应该指出，以下详细说明都是例示性的，旨在对本申请提供进一步的说明。除非另有指明，本发明使用的所有技术和科学术语具有与本申请所属技术领域的普通技术人员通常理解的相同含义。

需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本申请的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。

正如背景技术所介绍的，现有技术中存在多馈入交直流输电系统的同时换相失败问题，为了解决如上的技术问题，本申请提出了一种基于故障限流技术的多馈入交直流输电系统的故障分区方法。

在高压电网中，由于线路的电阻远小于电抗，为了方便推导，忽略电阻的影响，只考虑电抗。图1中所示为加入故障限流器前后的等效电路，u相当于电网中的接入电压，p、q、i、j相当于电网中的节点(以下所有电感电抗的右下角标中的i、j、p、q、m、n表示对应的节点之间的线路)，其中节点p处发生短路故障，短路电流为if，支路lij的电抗为x，流过支路lij的短路电流为ix。加入阻抗为δx的fcl后，支路lij的短路电流为ix-δix，短路电流为if-δif。下面推导δif和δx的关系式。

(1)在节点i，j采用戴维南定理，得出图2所示的等效电路为一个电压源和3个电阻串联的单口网络，其中xij,ij为等效电抗。则有，

其中，xij,ij为节点对(i,j)的自阻抗zij,ij的虚部值。

zij,ij＝zii+zjj-2zij(3)

则加入δx后，支路lij的短路电流为ix′

其中，u为支路lij开路时的电压。根据线性叠加原理，加入阻抗为δx的fcl后，相当于在支路lij注入δix的电流。

(2)采用节点对的概念，则有当节点对(i，j)注入电流δix时节点对(p，q)上的电位为δup,q-i,j，得到节点对(p，q)端口的戴维南等效电路。根据叠加原理和节点对互阻抗的定义得出图3为注入电流δix后对节点p短路电流影响的等效电路。其中x0为节点p短路时的接地电阻，此时考虑最严重的金属短路情况。

δu'＝δix·xij,pq(7)

其中，xij,pq为节点对(i，j)对(p，q)的互阻抗zij,pq的电抗部分。

zij,pq＝zip+zjq-ziq-zjp(8)

将式(5)代入式(6)和(7)，并且令xm＝xij,ij+x，k＝u·xij,pq/xpq,pq，所以可知

同样，非故障非安装fcl支路lmn的补偿电压δuy′也可以计算得到，表达式为

由公式可知，当δx为0时，δu′(δuy′同样)和δif两个变化量都为0，当δx从0开始增大时，两个变化量也随之增大，从而补偿线路短路造成的压降和抑制短路电流。

考虑到电网的线路较多，先通过关联度法选取安装fcl的候选支路。由于fcl安装地点对短路点的自阻抗影响很大，因此选取支路阻抗为控制参数，可以推导得到短路点自阻抗对lij上fcl参数zfcl的关联度表达式如下：

其中，λ为关联度系数；p为故障发生点；zpi和zpj分别为节点i和j与故障点p之间的互阻抗；zp′为p点自阻抗。显然，选取关联度更大的支路来配置fcl可以节约经济，发挥更大的作用。通过关联度法初步选取支路可以减少计算量。

从电网规划和经济性的角度考虑，优化配置的目标是尽可能减少安装fcl的数量和总阻抗值，并且可以达到解决同时换相失败现象。因此，本发明采用nsga-ii对fcl进行优化配置，具体目标函数和约束条件如下：

zfclmin≤zfcli≤zfclmin(i＝1,2，...，nfcl)(14)

δu-δu′≤0.2pu(15)

其中，nfcl为fcl的安装数量；δu为未发生故障的馈线出的未安装fcl时的压降，δu′为补偿压降，0.2pu是以未发生故障的馈线的原母线电压为标幺值。

设ω表示问题的解空间，在式(16)当ω中不存在另一个解u使得fi(u)≤fi(x),i＝1,2,…,r时，称x∈ω是该问题的一个pareto非支配解。

式中，x为解向量；f(x)为目标函数向量；h(x)和g(x)分别为等式约束和不等式约束。

设x^*为一非支配解，若在整个可行域中没有任何解支配x^*，则x^*在pareto意义下是最优的，称为pareto最优解，所有pareto解的集合称为pareto最优解集，记为x^*。

当解集还包含其他解时，以投入经济性作为最优解的最后选取的标准，根据实际经验，每套设备的安装及配套设施的成本是每单位欧姆的fcl成本的5至10倍，则选取成本最低的解作为最优解。

为了使得本领域技术人员能够更加清楚地了解本申请的技术方案，以下将结合具体的实施例与对比例详细说明本申请的技术方案。

如图4所示，提供了一个39节点交流电网。基于cigre单馈入标准模型建立多馈入直流输电模型，保留原等效交流电网，并在两条逆变站换流母线之间接入一个39节点交流电网，用以实现两条直流系统间的联络。篇幅限制，主要考虑39节点电网与直流系统间的联络主要通过节点2和16联系，假设与直流馈线2联系的节点16出发生接地短路故障，此时直流馈线2处的逆变器立刻发生换相失败，接下来将对fcl进行优化配置，通过故障分区，来避免直流馈线1同时发生换相失败。

首先通过关联度法对上述网络进行分析，求出与2和16关联度最大的候选支路，一共找出了11条，如下表所示。然后利用nsga-ii进行fcl的优化配置，形成故障分区，得到pareto最优解集如图5所示。

表1与节点2、6相关的支路统计

此时一共包含3个最优解，分别为安装1,2,3个fcl时，与之对应的fcl中阻抗标幺值0.103,0.081,0.035,这3个最优解都实现了目标函数的最优化。此时通过考虑成本继续优化，考虑到每套设备的安装及配套设施的成本是每单位欧姆fcl的5到10倍，所以得到最优解为配置1台fcl，对应的配置方案为在支路16-17上安装，阻抗标幺值为0.103。

完成故障分区之后，通过pscad建立的模型进行仿真，并在16-17处配置fcl。通过不断改变故障的严重程度，以熄弧角作为换相失败的判断依据，得到发生同时换相失败的概率为0，具体结果如图6所示的两种系统的cf可能性。可见在高压交直流输电系统中采用关联度法和nsga-ii相结合的故障分区技术，并结合经济性，可以快速找到fcl的安装位置完成避免同时换相失败的目标。

以上所述仅为本申请的优选实施例而已，并不用于限制本申请，对于本领域的技术人员来说，本申请可以有各种更改和变化。凡在本申请的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本申请的保护范围之内。