一种超声波电机伺服控制系统神经网络控制方法与流程

本发明属于电机控制器领域，特别涉及一种超声波电机伺服控制系统神经网络控制方法。

背景技术：

传统现有的超声波电机伺服控制系统的设计中由于滞后非线性的存在，使得系统的性能受到影响，对周期重复信号控制时有一定的误差。为了改善跟随的控制效果，我们设计了基于神经网络控制的超声波电机伺服控制系统。从伺服控制的实验中，我们发现力矩速度经过控制系统后关系基本是线性，且参数的变动、噪声、交叉耦合的干扰和摩擦力等因素几乎无法对于力矩输出造成影响，故基于神经网络控制的超声波电机伺服控制系统能有效的增进系统的控制效能，并进一步减少系统对于不确定性的影响程度，因此电机的力矩与速度控制可以获得较好的动态特性。

技术实现要素：

本发明的目的在于提供一种超声波电机伺服控制系统神经网络控制方法，该方法不仅控制准确度高，而且结构简单、紧凑，使用效果好。

为实现上述目的，本发明的技术方案是：一种超声波电机伺服控制系统神经网络控制方法，提供一超声波电机伺服控制系统，包括基座和设于基座上的超声波电机，所述超声波电机一侧输出轴与光电编码器相连接，超声波电机另一侧输出轴与飞轮惯性负载相连接，所述飞轮惯性负载输出轴经联轴器与力矩传感器相连接，所述光电编码器的信号输出端、力矩传感器的信号输出端分别接至控制系统；该方法建立在神经网络基础上，在减小跟踪动态误差的同时也使得伺服系统滞回最小，从而能获得更好的输入输出控制效能。

在本发明一实施例中，所述控制系统包括超声波电机驱动控制电路，所述超声波电机驱动控制电路包括控制芯片电路和驱动芯片电路，所述光电编码器的信号输出端与所述控制芯片电路的相应输入端相连接，所述控制芯片电路的输出端与所述驱动芯片电路的相应输入端相连接，以驱动所述驱动芯片电路，所述驱动芯片电路的驱动频率调节信号输出端和驱动半桥电路调节信号输出端分别与所述超声波电机的相应输入端相连接。

在本发明一实施例中，所述联轴器为弹性联轴器。

在本发明一实施例中，所述超声波电机、光电编码器、力矩传感器分别经超声波电机固定支架、光电编码器固定支架、力矩传感器固定支架固定于所述基座上。

在本发明一实施例中，该方法具体实现如下，

超声波电机驱动系统的动态方程可以写为：

其中ap＝-b/j，bp＝j/kt＞0，cp＝-1/j；b为阻尼系数，j为转动惯量，kt为电流因子，tf(v)为摩擦阻力力矩，tl为负载力矩，u(t)是电机的输出力矩，θr(t)为通过光电编码器测量得到的位置信号，为通过计算得到的速度信号，为通过计算得到的加速度信号；

x是电机转子的位移，表示速度，表示加速度；

为了消除电机摩擦力滞回造成的影响，采用神经网络控制；

考虑具有滞回siso非线性系统

其中，x＝[x1,x2,...,xn]^t是系统状态；a(x)和b(x)是未知的平滑函数；de(t)表示系统不确定性，包括外部干扰和建模误差，|de(t)|≤d0；ω(t)是由(2)、(3)给出

ω(t)＝p0v(t)-d[v](t)(2)

其中，为方便起见，对于任何给定的滞回初始状态ψ1，fr[v；ψ1]由fr[v]表示；通过该滞回模型，系统(1)变为

系统的目的是设计稳定的控制律v(t)以强制状态向量x＝[x1,x2,...,xn]^t尽可能接近给定轨迹

对于此系统，做出以下假设：

假设1：b(x)的符号是已知的，并且存在一个常数b0＞0，使得b0＜|b(x)|；由于b(x)的符号已知，并且b(x)不等于零，可以假设b(x)＞0；

假设2：存在平滑函数使得且独立于状态xn；

假设3：所需的轨迹xd是可用的；

假设4：存在已知的常数p0min＞0和已知函数pmax(r)，使得对于所有r∈[0,r]，p0＞p0min和p(r)≤pmax(r)；

对于假设4，基于密度函数p(r)的性质，设定p(r)的上界pmax是合理的；这里p0min＞0必须满足，否则p0＝0意味着ω(t)＝0；

为了简化，取

其中，由假设1，2和3，g(x)与xn无关，且0＜g(x)≤1；

将跟踪误差向量定义为过滤的跟踪误差s(t)为

s(t)可以写为和λ^t＝[λ^n-1,(n-1)λ^n-2,...,(n-1)λ]；

公式(5)中给出的定义具有以下属性：

等式s(t)＝0定义中的时变超平面，其中跟踪误差向量指数衰减为零；如果和|s(t)|≤ε，其中，ε是常数，那么对于

控制器设计：

首先假设非线性函数a(x)和b(x)是已知的，密度函数p(r)可用，并且系统不确定度de(t)＝0；pi模型(2)将滞回分解为两部分：线性可逆分量p0v(t)和非线性滞后分量d[v](t)；如果d[v](t)＝0，则系统输入为ω(t)＝d[v](t)，存在理想的反馈控制v*；在该控制下，状态向量x将跟随期望的轨迹xd渐近；

考虑状态反馈控制

其中，δ＞0是常数，

根据(5)，系统(4)的输入v*(t)的时间导数可以写为

定义一个lyapunov函数v1的时间导数等于

由于0＜g(x)＜1，因此

上述不等式的解决方案满足

|b(x)|≥b0＞0，limt→∞v1(t)＝0表示limt→∞s＝0；

当函数a(x)和b(x)已知并且滞回函数p(r)可用时，则使用(6)中定义的控制输入v*，跟踪误差矢量渐近收敛；如果d[v](t)＝0，则系统不确定度de(t)＝0；

当a(x)、b(x)和p(r)未知时，(6)给出的控制器v*不能实现；此时，一个合理的方法是使用估计的v近似v*(t)；在假设1和2中，a(x)、b(x)相对于x(t)和xd是连续的；使用神经网络方法得到近似的

取z＝(x^t,s,s/δ,μ)^t

其中，l是神经网络的节点数，φ(z)是基函数向量，近似误差εl满足|εl|≤ε0；θ*是理想神经网络权重，

现在将未知非线性问题转化为估计理想参数向量θ^*；令是理想神经网络权重θ^*的估计，并且控制器vn(t)被选择为

适应规则为

其中，γ、σ＞0是自适应增益系数；

为了消除由d[v](t)引起的影响，注意到d[v](t)由权重函数p(r)确定，它与时间无关；因此可以将其视为每个固定r的参数，并通过适应规则进行调整；令是任何r处p(r)的估计；

适应规则为

其中，γ>0和η>0是自适应参数；

自适应控制器定义如下

其中，vn和vh由(14)和(16)给出。将v(t)代入系统(4)中，s的时间导数重写为

选择lyapunov函数

v的时间导数为

利用适应规则(15)

为了简化(24)，从(16)有

由于并将(17)代入上式中，有

因此

此外使用以下不等式

并注意到0＜g(x)≤1,|εl|≤ε0，|de(t)|≤d0；

取

其中，λmax是γ^-1的最大特征值；上述不等式满足

有

从v的定义，可以得到s，和是有界的；特别：

(37)中滤波跟踪误差的界限是t的函数，并且取决于初始值v(t0)；可以证明跟踪误差向量收敛到一个集合，这不依赖于初始条件v(t0)；令p＝d/dt为拉普拉斯算子；

从(37)开始，y1(t)被界定

通过将不等式从i＝2整合到i＝n-1，对于n≥3，有

由于和满足上述不等式，并且其中c和τ是(33)和(35)中给出的常数；下面给出

它们在时λ＝τ/2，而时，λ为其他值；

同样，对于取

z1(p)＝yn-i-1(p)

由于作为结论，总结如下：

考虑非线性系统(1)，其中滞回满足假设1-4，如果鲁棒自适应控制器由(18)与适应法(15)和(17)规定，则对于任何有界的初始条件，所有闭环信号都是有界的，状态向量x(t)收敛到

其中，τ和c是(33)和(35)中给出的常数；

在上述中，收敛集的约束由τ和c确定；由于τ是由控制器参数δ、σ、λmax、γ和η决定的常数；c取决于控制器参数和设备的性质；可以通过选择系统属性的合适参数来调整收敛集的边界；综上所述，可以从神经网络方法得到近似的

相较于现有技术，本发明具有以下有益效果：本发明方法使用神经网络控制的超声波电机伺服控制器，系统在具有滞回系统的跟踪效果上有着显著的改善且参数的变动、噪声、交叉耦合的干扰和摩擦力等因素几乎无法对于运动系统效果造成影响，故基于神经网络控制的超声波电机伺服控制系统能有效的增进系统的动态性能，并进一步减少系统对于不确定性的影响程度，提高了控制的准确性，可以获得较好的动态特性；此外，本发明方法采用的装置设计合理，结构简单、紧凑，制造成本低，具有很强的实用性和广阔的应用前景。

附图说明

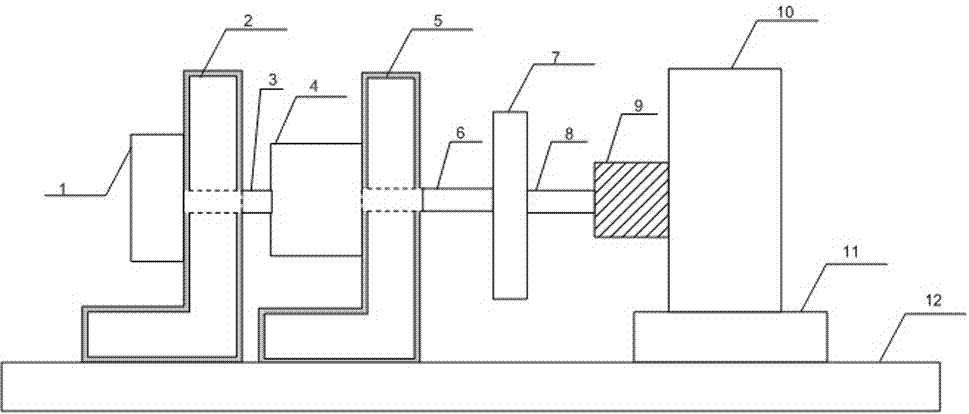
图1是本发明实施例的结构示意图。

图2是本发明实施例的控制电路原理图。

图中，1-光电编码器，2-光电编码器固定支架，3-超声波电机一侧输出轴，4-超声波电机，5-超声波电机固定支架，6-超声波电机另一侧输出轴，7-飞轮惯性负载，8-飞轮惯性负载输出轴，9-弹性联轴器，10-力矩传感器，11-力矩传感器固定支架，12-基座，13-控制芯片电路，14-驱动芯片电路，15、16、17-光电编码器输出的a、b、z相信号，18、19、20、21-驱动芯片电路产生的驱动频率调节信号，22-驱动芯片电路产生的驱动半桥电路调节信号，23、24、25、26、27、28-控制芯片电路产生的驱动芯片电路的信号，29-超声波电机驱动控制电路。

具体实施方式

下面结合附图，对本发明的技术方案进行具体说明。

本发明提供了一种超声波电机伺服控制系统滑模控制方法，提供一超声波电机伺服控制系统，包括基座12和设于基座12上的超声波电机4，所述超声波电机一侧输出轴3与光电编码器1相连接，超声波电机另一侧输出轴6与飞轮惯性负载7相连接，所述飞轮惯性负载输出轴8经联轴器(弹性联轴器9)与力矩传感器10相连接，所述光电编码器1的信号输出端、力矩传感器10的信号输出端分别接至控制系统；所述控制系统包括超声波电机驱动控制电路29，所述超声波电机驱动控制电路29包括控制芯片电路13和驱动芯片电路14，所述光电编码器1的信号输出端与所述控制芯片电路13的相应输入端相连接，所述控制芯片电路13的输出端与所述驱动芯片电路14的相应输入端相连接，以驱动所述驱动芯片电路14，所述驱动芯片电路14的驱动频率调节信号输出端和驱动半桥电路调节信号输出端分别与所述超声波电机4的相应输入端相连接；所述驱动芯片电路14产生驱动频率调节信号和驱动半桥电路调节信号，对超声波电机输出a、b两相pwm的频率、相位及通断进行控制。通过开通及关断pwm波的输出来控制超声波电机的启动和停止运行；通过调节输出的pwm波的频率及两相的相位差来调节电机的最佳运行状态。所述超声波电机4、光电编码器1、力矩传感器10分别经超声波电机固定支架5、光电编码器固定支架2、力矩传感器固定支架固11定于所述基座12上。该方法建立在神经网络基础上，在减小跟踪动态误差的同时也使得伺服系统滞回最小，从而能获得更好的输入输出控制效能。

本发明一种基于神经网络的超声波电机伺服控制系统，整个控制器的系统建立在神经网络控制器的基础上，引入神经网络参数消除动态误差，鲁棒自适应控制器确保所有闭环信号都是有界的，最后状态向量的误差和期望的轨迹收敛到给定曲线，从而能获得更好的控制效能。如上所述，在本实施例中，所述控制系统的硬件电路包括超声波电机驱动控制电路，所述超声波电机驱动控制电路包括控制芯片电路和驱动芯片电路，所述基于神经网络的超声波电机伺服控制器设于所述控制芯片电路中。

基于神经网络的超声波电机伺服控制系统用于对具有滞回特性的系统进行控制，整个控制器的系统建立在神经网络的基础上，鲁棒自适应控制器确保所有闭环信号都是有界的，状态向量的误差和期望的轨迹收敛到给定曲线，从而能获得更好的控制效能。

本发明方法具体实现如下：

超声波电机驱动系统的动态方程可以写为：

其中ap＝-b/j，bp＝j/kt＞0，cp＝-1/j；b为阻尼系数，j为转动惯量，kt为电流因子，tf(v)为摩擦阻力力矩，tl为负载力矩，u(t)是电机的输出力矩，θr(t)为通过光电编码器测量得到的位置信号，为通过计算得到的速度信号，为通过计算得到的加速度信号；

x是电机转子的位移，表示速度，表示加速度；

为了消除电机摩擦力滞回造成的影响，采用神经网络控制；

考虑具有滞回siso非线性系统

其中，x＝[x1,x2,...,xn]^t是系统状态；a(x)和b(x)是未知的平滑函数；de(t)表示系统不确定性，包括外部干扰和建模误差，|de(t)|≤d0；ω(t)是由(2)、(3)给出

ω(t)＝p0v(t)-d[v](t)(2)

其中，为方便起见，对于任何给定的滞回初始状态ψ1，fr[v；ψ1]由fr[v]表示；通过该滞回模型，系统(1)变为

系统的目的是设计稳定的控制律v(t)以强制状态向量x＝[x1,x2,...,xn]^t尽可能接近给定轨迹

对于此系统，做出以下假设：

假设1：b(x)的符号是已知的，并且存在一个常数b0＞0，使得b0＜|b(x)|；由于b(x)的符号已知，并且b(x)不等于零，可以假设b(x)＞0；

假设2：存在平滑函数使得且独立于状态xn；

假设3：所需的轨迹xd是可用的；

假设4：存在已知的常数p0min＞0和已知函数pmax(r)，使得对于所有r∈[0,r]，p0＞p0min和p(r)≤pmax(r)；

对于假设4，基于密度函数p(r)的性质，设定p(r)的上界pmax是合理的；这里p0min＞0必须满足，否则p0＝0意味着ω(t)＝0；

为了简化，取

其中，由假设1，2和3，g(x)与xn无关，且0＜g(x)≤1；

将跟踪误差向量定义为过滤的跟踪误差s(t)为

s(t)可以写为和λ^t＝[λ^n-1,(n-1)λ^n-2,...,(n-1)λ]；

公式(5)中给出的定义具有以下属性：

等式s(t)＝0定义中的时变超平面，其中跟踪误差向量指数衰减为零；如果和|s(t)|≤ε，其中，ε是常数，那么对于

控制器设计：

首先假设非线性函数a(x)和b(x)是已知的，密度函数p(r)可用，并且系统不确定度de(t)＝0；pi模型(2)将滞回分解为两部分：线性可逆分量p0v(t)和非线性滞后分量d[v](t)；如果d[v](t)＝0，则系统输入为ω(t)＝d[v](t)，存在理想的反馈控制v*；在该控制下，状态向量x将跟随期望的轨迹xd渐近；

考虑状态反馈控制

其中，δ＞0是常数，

根据(5)，系统(4)的输入v*(t)的时间导数可以写为

定义一个lyapunov函数v1的时间导数等于

由于0＜g(x)＜1，因此

上述不等式的解决方案满足

|b(x)|≥b0＞0，limt→∞v1(t)＝0表示limt→∞s＝0；

当函数a(x)和b(x)已知并且滞回函数p(r)可用时，则使用(6)中定义的控制输入v*，跟踪误差矢量渐近收敛；如果d[v](t)＝0，则系统不确定度de(t)＝0；

当a(x)、b(x)和p(r)未知时，(6)给出的控制器v*不能实现；此时，一个合理的方法是使用估计的v近似v*(t)；在假设1和2中，a(x)、b(x)相对于x(t)和xd是连续的；使用神经网络方法得到近似的

取z＝(x^t,s,s/δ,μ)^t

其中，l是神经网络的节点数，φ(z)是基函数向量，近似误差εl满足|εl|≤ε0；θ*是理想神经网络权重，

现在将未知非线性问题转化为估计理想参数向量θ*；令是理想神经网络权重θ*的估计，并且控制器vn(t)被选择为

适应规则为

其中，γ、σ＞0是自适应增益系数；

为了消除由d[v](t)引起的影响，注意到d[v](t)由权重函数p(r)确定，它与时间无关；因此可以将其视为每个固定r的参数，并通过适应规则进行调整；令是任何r处p(r)的估计；

适应规则为

其中，γ>0和η>0是自适应参数；

自适应控制器定义如下

其中，vn和vh由(14)和(16)给出。将v(t)代入系统(4)中，s的时间导数重写为

选择lyapunov函数

v的时间导数为

利用适应规则(15)

为了简化(24)，从(16)有

由于并将(17)代入上式中，有

因此

此外使用以下不等式

并注意到0＜g(x)≤1,|εl|≤ε0，|de(t)|≤d0；

取

其中，λmax是γ^-1的最大特征值；上述不等式满足

有

从v的定义，可以得到s，和是有界的；特别：

(37)中滤波跟踪误差的界限是t的函数，并且取决于初始值v(t0)；可以证明跟踪误差向量收敛到一个集合，这不依赖于初始条件v(t0)；令p＝d/dt为拉普拉斯算子；

从(37)开始，y1(t)被界定

通过将不等式从i＝2整合到i＝n-1，对于n≥3，有

由于和满足上述不等式，并且其中c和τ是(33)和(35)中给出的常数；下面给出

它们在时λ＝τ/2，而时，λ为其他值；

同样，对于取

z1(p)＝yn-i-1(p)

由于作为结论，总结如下：

考虑非线性系统(1)，其中滞回满足假设1-4，如果鲁棒自适应控制器由(18)与适应法(15)和(17)规定，则对于任何有界的初始条件，所有闭环信号都是有界的，状态向量x(t)收敛到

其中，τ和c是(33)和(35)中给出的常数；

在上述中，收敛集的约束由τ和c确定；由于τ是由控制器参数δ、σ、λmax、γ和η决定的常数；c取决于控制器参数和设备的性质；可以通过选择系统属性的合适参数来调整收敛集的边界；综上所述，可以从神经网络方法得到近似的可以实现所期望的较小跟踪误差。

本发明使用神经网络可以对具有滞回的系统进行控制，从而减小控制系统滞回对系统精度的影响。

以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。