计及谐波影响的静态电压稳定性分析方法与流程
本发明属于含有非线性负荷及分布式电源的电网可靠性领域,涉及分析谐波对电网可靠性影响的方法,具体为计及谐波影响的静态电压稳定性分析方法。
背景技术
电力系统波形畸变问题最早提出于上世纪二、三十年代的德国,到五、六十年代,各国工程师就换流器的谐波问题已进行了大量研究,并得到了大量的研究成果。八十年代开始,我国铁路电气化迅速发展,由此带来的显著的谐波问题成为我国谐波理论和技术发展的重要契机。近年来,随着电力负荷的多样化发展以及电力电子装置的大量应用,非线性负荷占负荷整体的比例逐年攀高,当非线性负荷接入电力系统工作时,向其中注入了大量谐波,是电力系统电压波形的最主要影响因素。与负荷直接相连的配电网电能质量治理更是受到了极大的挑战。此外,由于化石能源的日益枯竭以及人类对清洁能源的开发利用,分布式发电技术得以大力发展,配电网正朝着多源、灵活、可持续发展的主动配电网方向发展,在缓解电网压力的同时,由于可再生能源间歇性、随机性的特点,以及通过电力电子装置的并网方式,也将给配电网带来更多的电能质量问题,其中谐波问题是电力运营部门的主要关注点。
技术实现要素:
本发明为了解决谐波对电力系统的影响的问题,针对负荷随机波动、配电网多谐波源、负荷、谐波源随机波动等问题,建立了一种计及谐波影响的电力系统静态电压稳定性评估方法。
本发明是采用如下的技术方案实现的:计及谐波影响的静态电压稳定性分析方法,包括元件模型搭建及谐波潮流计算方法和静态电压稳定性分析方法;
元件模型搭建及谐波潮流计算方法中包括谐波源模型搭建、输电线路模型搭建、负荷模型搭建和利用解耦法求解谐波潮流;
谐波源模型搭建:
在系统中有且仅有一个谐波源的情况下,判断谐波源的类型,若该谐波源为分布式电源,则在计算基波潮流时,将分布式电源所在节点视为pv节点,在计算谐波潮流时,将分布式电源所在节点视为平衡节点;若该谐波源为非线性负荷,则计算基波潮流时,将非线性负荷所在节点视为pq节点,计算谐波潮流时,将非线性负荷所在节点视为平衡节点;
若系统中存在多个谐波源,但谐波源均为非线性负荷,在计算基波潮流时,将非线性负荷所在节点视为pq节点,在计算谐波潮流时,将非线性负荷含量最多的节点视为平衡节点,其余非线性负荷所在节点视为pv节点;如果系统中既含有分布式电源,又含有非线性负荷,在计算基波潮流的时候,将分布式电源所在节点视为pv节点,非线性负荷所在节点视为pq节点,计算谐波潮流时,将容量较大的分布式电源所在节点作为平衡节点,其余谐波源所在节点视为pv节点;若系统中谐波源均为分布式电源,在计算基波潮流时,将分布式电源所在节点视为pv节点,在计算谐波潮流时,将容量最大的一个分布式电源所在节点视为平衡节点,其余分布式电源所在节点设为pv节点。
计算谐波潮流时,会出现因为系统中pv节点过多而导致的潮流不收敛的情况,本文根据谐波源的容量与谐波源的谐波特性进行分组,将容量相近、谐波特性相同的谐波源组统一计算,每个谐波源组进行一次谐波潮流计算,用叠加法进行计算。
输电线路模型搭建:输电线路以集中参数的等值π型电路表示,等值π型电路参数为分布参数的简单集中,即:
负荷模型搭建:谐波阻抗计算如式所示:
利用解耦法求解谐波潮流:(1)计算基波潮流:迭代计算在不考虑谐波影响下,求解出电力系统各个节点的电压u1i,i表示电力系统中各个节点;(2)计算谐波潮流:利用谐波源模型、输电线路模型和负荷模型更新电力系统状态,利用基波潮流计算出来的各个节点的基波电压u1i和非线性负荷的负荷模型更新电力系统中非线性负荷的状态,通过迭代的方式求取电力系统中各个节点的谐波电压uhj;(3)通过电力系统中各个节点的谐波电压uhj,利用叠加法求解各个节点电压的标幺值uhi,
静态电压稳定性分析方法包括设定电压灵敏度、电压畸变灵敏度两项指标和静态电压稳定性分析;
设定电压灵敏度、电压畸变灵敏度两项指标:电压灵敏度指标
电压灵敏度指标α1可变形为
静态电压稳定性分析:
本发明以电压灵敏度指标与电压畸变灵敏度指标为依据,提出了得出薄弱节点、安全域与敏感节点结合的静态电压稳定性识别方法,识别过程简单,容易实现。
电压灵敏度指标与电压畸变灵敏度指标越小,则说明节点越薄弱。
将系统根据线路结构进行分区,通过电压灵敏度指标与电压畸变灵敏度指标对所分区域的安全域进行划分,若不会有电压风险,则为安全区;若在某些运行方式下有电压风险,则为警戒区,若存在电压风险,则为限制区。
电压畸变灵敏度指标与电压灵敏度指标的比值α1/α2=thdu,体现了节点的电压畸变率,可因此判断系统对谐波的敏感节点。
薄弱节点关注的是系统临界运行状态下,容易发生崩溃的部分;安全域强调系统临界运行状态下,系统整体的状态;敏感节点则注重谐波对节点的影响,将薄弱节点、安全域与敏感节点相结合,能够更好地描述谐波对系统的影响。
将拉丁超立方抽样引入谐波潮流计算中,通过产生多组初始负荷矩阵,同时考虑线性负荷的随机波动与非线性负荷的不确定性,并对每种初始负荷矩阵求解系统静态电压稳定性,减小初始负荷对系统静态电压稳定性的影响;
利用解耦法与改进二分搜索法,在谐波源的接入位置、初始负荷确定的状态m下,求得计及谐波影响的情况下电力系统处于状态m临界状态下的节点电压ui及电压畸变率thdui,进而求得临界状态下的电压灵敏度指标α1、电压畸变灵敏指标α2,电压灵敏度指标α1和电压畸变灵敏指标α2数值最低的为状态m临界状态下电力系统薄弱节点,电力系统中各个节点的电压灵敏度指标α1,电压畸变灵敏指标α2构成状态m临界状态下电力系统的安全域,敏感节点为谐波含量变化对系统静态电压稳定性的影响最大的节点,对所有的状态m进行分析,m个状态全部分析结束,统计分析不同状态下,系统的薄弱节点、安全域与敏感节点,进而分析系统的静态电压稳定性。
与现有研究相比,本发明所具有的有益效果如下:
(1)目前的研究中,对于谐波的研究都是在系统正常运行状况下的研究,并没有考虑到临界运行状态。本发明在逼近系统临界运行状态时考虑了谐波的影响,并利用解耦法求解系统的谐波潮流,得到系统在谐波影响下临界运行状态。
(2)目前的研究中,电压稳定性分析方法包括逐点法与安全域方法,逐点法难以对电力系统的运行状态提出整体评价,安全域方法没有考虑谐波影响,本发明提出电压灵敏度、电压畸变灵敏度两项指标,评估计及谐波影响的系统薄弱节点与安全域。
(3)目前的研究中,有文献考虑谐波源的不确定性,但是同时考虑谐波源和线性负荷的不确定性尚未有人研究。本专利将拉丁超立方抽样用于不确定性谐波潮流分析中,同时考虑了系统中线性负荷与非线性负荷的不确定性,对电网静态电压稳定性进行统计分析。
(4)本专利将谐波潮流计算方法与改进二分搜索法相结合,计及谐波对电压稳定性的影响,减小了计算量,提高了计算速度。
附图说明
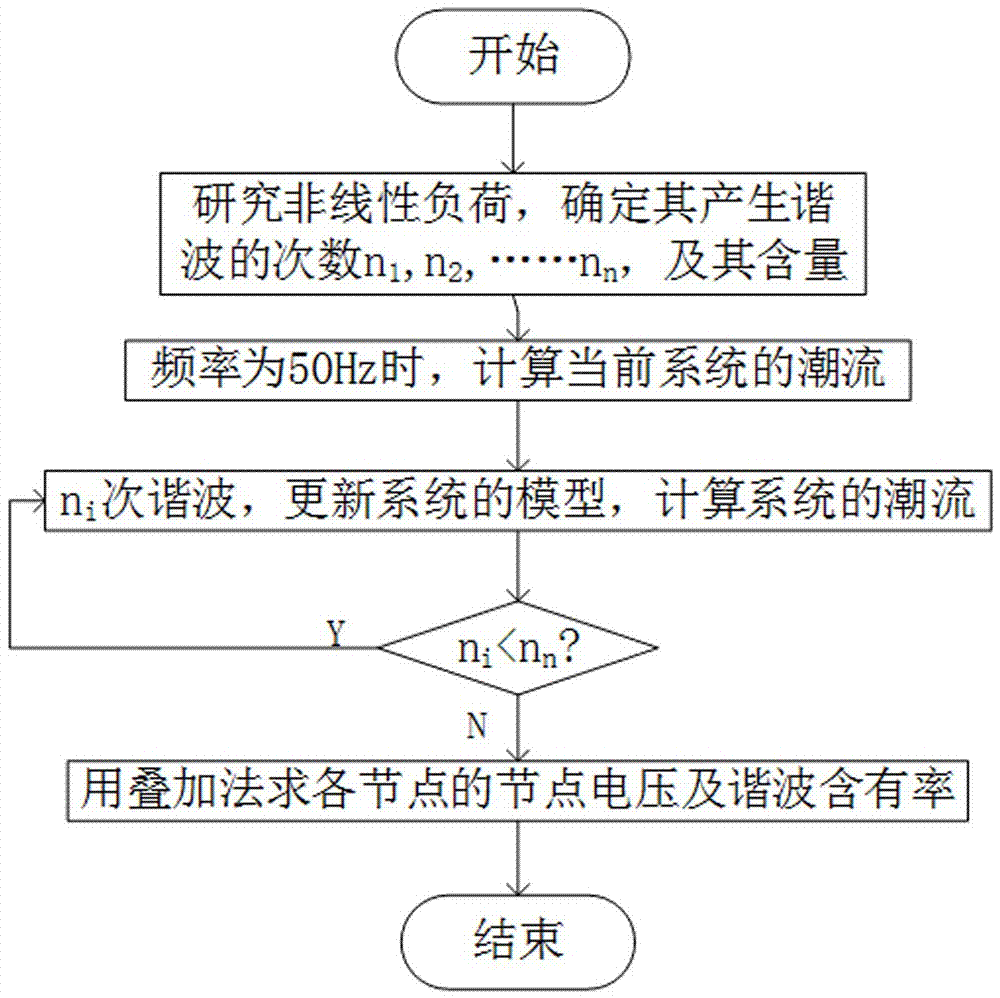
图1为本发明解耦法计算谐波潮流流程图。
图2为本发明计及谐波影响的静态电压稳定性分析方法流程图。
图3为本发明所使用的ieee33节点系统接线图。
图4为本发明单谐波源电压灵敏度指标柱状图。
图5为本发明单谐波源电压畸变灵敏度指标柱状图。
图6为本发明多谐波源电压灵敏度指标与电压畸变灵敏度指标结果对比。
图7为本发明系统静态电压失稳临界状态下的电压灵敏度分布曲面。
图8为本发明系统静态电压失稳临界状态下的电压畸变灵敏度分布曲面。
图9为本发明系统静态电压失稳临界状态下的电压灵敏度局部分布曲面。
图10为本发明系统静态电压失稳临界状态下的电压灵敏度局部分布曲面。
具体实施方式
本发明提供了一种计及谐波影响的静态电压稳定性分析方法。首先,在逼近系统临界运行状态时考虑了谐波的影响,并利用解耦法求解系统的谐波潮流,得到系统在谐波影响下临界运行状态。第二,提出电压灵敏度、电压畸变灵敏度两项指标,评估计及谐波影响的系统薄弱节点与敏感节点。第三,将拉丁超立方抽样用于不确定性谐波潮流分析中,同时考虑了系统中线性负荷与非线性负荷的不确定性,对电网静态电压稳定性进行统计分析。具体方案如下:
元件模型及谐波潮流计算
谐波潮流计算是研究电力潮流中谐波问题的重要手段,通过谐波潮流计算,可以了解全网络谐波潮流的分布情况,得出各节点的谐波指标,是评估电力系统稳定性的重要依据。所有元件状态的组合即为潮流,故在进行谐波潮流计算中,最重要的是设定供电系统各元件的谐波参数、模型以及其连接状况,下面讨论各元件的谐波参数及谐波潮流的计算方法。
谐波源模型
在电力系统中,谐波源主要有两类,一类是传统非线性设备,如电弧炉,另外一类则是现代电力电子非线性设备,如电动汽车充电桩及分布式电源。表1是电动汽车充电桩各次谐波含有率,表2是电弧炉各次谐波含有率。
表1电动汽车充电桩各次谐波电流含有率
tab1thecontentofeachharmoniccurrentinchargingpilesofelectricvehicles
表2电弧炉各次谐波含有率
tab2allharmoniccontentofeaf
在数学上,谐波源可统一为式(1)所示的节点电压和符合控制参数的函数,产生的谐波电流可以通过该式获得:ih=fh(u1j,u2j,…,uhj,c1,c2,…,ch)h=1,2,…,h,(1)其中,ih是该谐波源产生的第h次谐波电流,u1j,u2j,…,uhj是谐波源注入节点的情况下,节点j的基波电压及各次谐波电压,c1,c2,…,ch是谐波源的控制参数,h为谐波最大次数。理论上,该函数能计算出准确的谐波信息,但由于需要对不同谐波源分别建模且计算复杂,在谐波源种类繁多的实际电力系统中并不适用。
因此,本文对于谐波源的处理,在系统中有且仅有一个谐波源的情况下,判断谐波源的类型,若该谐波源为分布式电源,则在计算基波潮流时,将分布式电源所在节点视为pv节点,在计算谐波潮流时,将分布式电源所在节点视为平衡节点;若该谐波源为非线性负荷,则计算基波潮流时,将非线性负荷所在节点视为pq节点,计算谐波潮流时,将非线性负荷所在节点视为平衡节点;
若系统中存在多个谐波源,但谐波源均为非线性负荷,在计算基波潮流时,将非线性负荷所在节点视为pq节点,在计算谐波潮流时,将非线性负荷含量最多的节点视为平衡节点,其余非线性负荷所在节点视为pv节点;如果系统中既含有分布式电源,又含有非线性负荷,在计算基波潮流的时候,将分布式电源所在节点视为pv节点,非线性负荷所在节点视为pq节点,计算谐波潮流时,将容量较大的分布式电源所在节点作为平衡节点,其余谐波源所在节点视为pv节点;若系统中谐波源均为分布式电源,在计算基波潮流时,将分布式电源所在节点视为pv节点,在计算谐波潮流时,将容量最大的一个分布式电源所在节点视为平衡节点,其余分布式电源所在节点设为pv节点。
第h次合成谐波电压的叠加法则,可以根据式(2)进行计算:
式中,uhi表示对所考虑的一组谐波源(概率统计值)计算出的(第h次)i节点处合成谐波电压值;uhj为要进行合成的单个谐波电压(第h次)的值,j表示谐波源所在的节点。
表3叠加指数∝:
tab3overlayindex∝
输电线路模型
输电线路以集中参数的等值π型电路表示,等值电路参数常常为分布参数的简单集中,即:
式中,r01、x01、b01分别为线路单位长度的基波电阻、电抗和电纳;l为线路长度,当线路中的电流为h次谐波时:
式中,zch和rh分别为h次谐波时线路的特性阻抗和传播函数,均为复数,具体计算如下:
式中,yoh为h次谐波时,系统的电导,yoh=jhb01;zoh为h次谐波时,系统的阻抗,zoh=hr01+jhx01。
负荷模型
负荷包括普通线性负荷与非线性负荷。考虑到负荷随机波动的因素对电力系统的影响,负荷采用正态分布,以系统给定的数值为均值,方差为0.05,以获取系统各个节点的随机负荷状态。
再考虑到集肤效应后,谐波对输电线路的影响不可忽略,谐波阻抗计算如式(6)-(7)所示:
式中,ui为节点i的实际电压;s为节点视在功率;rs,xs分别为基波时等值电动机的电阻和电抗。
利用解耦法求解谐波潮流
电力系统中,一般谐波相对基波数值较小,所以基波潮流基本不受谐波潮流的影响。解耦法利用这一点,简化求解,求解思路如下所示:
(1)计算基波潮流:迭代计算在不考虑谐波影响下,求解出电力系统各个节点的电压u1i;
(2)计算谐波潮流:利用谐波源模型、输电线路模型和负荷模型跟新系统状态,利用基波潮流计算出来的各个节点的电压u1i和非线性负荷的负荷模型更新系统中非线性负荷的状态,通过迭代的方式求取系统中各个节点的谐波电压uhj;
(3)通过系统中典型谐波源产生的各个节点的谐波电压uhj,利用叠加法求解各个节点电压的标幺值uhi,计算在谐波影响下,系统中各个节点的电压及电压畸变率。
流程图如图1所示。
《电力系统安全稳定导则》将电压稳定性定义为电力系统受到小的或大的扰动后,系统能保持或者恢复到容许范围内,不发生电压崩溃的能力。谐波可视为电力系统的扰动,在电力系统电力电子化的过程中,研究谐波对电力系统电压稳定性的影响十分必要。
计及谐波影响的静态电压稳定性分析方法
谐波对电力系统的影响主要体现在两个方面,其一,非线性负荷及分布式电源作为谐波源,可能抬高节点电压;其二,该节点电压畸变率将会大幅度升高,影响设备的正常运行。
节点崩溃电压是指系统临界运行时,该节点的电压水平。崩溃电压可以在一定程度上反映节点的强度,理论上崩溃电压越高,节点越坚强,因为系统临界运行时,该节点依然能保持相对正常的电压水平。
电压波形畸变的程度用电压正弦波畸变率来衡量,也称电压谐波畸变率。电压谐波畸变率以各次谐波电压的均方根值与基波电压有效值之比的百分数来表示:
式中,thdui表示节点i的电压畸变率,u1i表示节点i的基波电压,uhi表示节点i的第h次谐波电压。
灵敏度指标是一种状态指标,可以反映系统某一运行状态的特性,将系统逼近到即将发生电压失稳的临界状态下求取该状态指标,能够反映当系统临近电压失稳时电网中各个节点电压的灵敏性,更加准确地反映了电网中各个节点对于干扰的敏感度。
为考虑含有谐波源的电网中,谐波对系统静态电压稳定性的影响,本文提出了电压灵敏度指标与电压畸变灵敏度指标,对比体现电压畸变率对系统静态电压稳定性的影响。指标定义如下:
电压灵敏度指标α1:
电压畸变灵敏指标α2:
式中,节点i的实际电压为ui;节点i由谐波引起的电压变化为δui,电压灵敏度指标α1表示在含有谐波源的系统中,不考虑谐波影响的情况,电压畸变灵敏度α1表示在含有谐波源的系统中,考虑谐波影响的情况。电压值
电压灵敏度指标:
则电压畸变灵敏度指标:
所定义指标α1、α2为只和各个节点的电压畸变率thdui有关,可以体现谐波对电力系统静态电压稳定性的影响。显然,电压灵敏度指标和电压畸变灵敏度指标越大,节点发生崩溃的可能性越小。
计及谐波影响的静态电压稳定性分析方法计算步骤
考虑到系统中非线性负荷的变化及线性负荷的随机波动,本文将拉丁超立方抽样引入谐波潮流计算中,利用解耦法与改进二分搜索法,通过多次计算,可以求得系统处于某种临界状态下的节点电压ui及电压畸变率thdui,电压灵敏度指标α1,电压畸变灵敏指标α2,统计分析谐波对系统静态电压稳定性的影响,求得计及谐波影响的系统薄弱节点、安全域与敏感节点;敏感节点为体现谐波含量变化对系统静态电压稳定性的影响。
安全域方法是在逐点法基础上发展起来的方法,他从域的角度出发考虑问题,描述的是整体可安全稳定运行的区域。
以ieee33节点系统为例,利用matlab软件进行仿真分析。在计及谐波的影响下,先后仿真了系统中含有一个谐波源与多个谐波源的情况,求取系统的安全域。
对比图4,图5中薄弱节点增加,18节点成为薄弱节点的概率减小,18节点成为薄弱节点的概率增加,说明18节点对系统谐波较为敏感。
从图6中可以看出来,18节点成为薄弱节点的概率增加,33节点成为薄弱节点的概率减小,所以18节点对系统谐波较为敏感。
对比图7与图8,二者变化趋势大致相同,说明考虑谐波与不考虑谐波的情况下,系统中薄弱节点与安全域并没有发生变化。
图9中,18节点与33节点的电压灵敏度指标较为接近;图10中,18节点的电压畸变灵敏度指标明显小于33节点,说明在考虑谐波的情况下,18节点成为系统薄弱节点的概率增加,说明18节点对系统谐波变化较为敏感。
- 还没有人留言评论。精彩留言会获得点赞!