一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法与流程

本发明属于静止变频器负载换相数值仿真技术领域，特别涉及一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法。

背景技术：

静止变频器(sfc)在抽水蓄能、调相机等启动过程中被大规模使用，sfc主要的作用在于通过变化定子电流形成的磁场拖动转子旋转，并根据转子转速的改变定子电流形成的磁场。sfc启动旋转电机的过程分为强迫换相阶段及负载自然换相阶段。负载自然换相发生在在一定转速下，机端电压已经能够形成足够的换相电压，换相时不会导致定子电流换相失败。

负载自然换相时，由于机端电压在发生变化，其换相过程中的换相重叠角μ将不会保持恒定，机端电压与换相重叠角存在一个动态关系，如式1，式2所示。

注：所有变量及参数说明见计算实例。

国内不少文献开展了负载换相阶段的仿真工作，但均未考虑机端电压变化导致换相重叠角μ变化的情况。文献[1-4]中假设仿真过程中μ保持不变，ik保持不变。这样的假设是与仿真过程存在明显矛盾的。因此有必要考虑机端电压u值变化时，μ值变化对数值仿真结果的影响。

相关文献及专利有：

(1)田立军，陆于平.抽水蓄能电动发电机起动过程数字仿真[j].电力系统自动化，1997，21(7).

(2)李玉玲，王自涛，戈宝军.同步电动机静止变频自然换流起动过程研究[j].哈尔滨理工大学学报，2002，5(1).

(3)戈宝军，李玉玲，李波.抽水蓄能电机静止变频器起动过程分析[j].电机与控制学报.2002，6(3).

(4)戈宝军，李玉玲.励磁控制下抽水蓄能电机静止变频器起动研究[j].电机与控制学报.2003，7(3).

文献[1]分析了抽水蓄能电动发电机起动过程数字仿真过程，但并未考虑换相重叠角μ的变化，假定转速变化过程中μ恒定，因而存在矛盾。本专利在文献(1)的基础上考虑了μ的变化，在仿真过程中消除了公式的矛盾，相当于对文献(1)进行了发展。

文献[2-4]沿用了文献[1]的数字仿真模型，因而同样未考虑换相重叠角μ的变化，假定转速变化过程中μ恒定，因而存在矛盾。

技术实现要素：

本发明所要解决的技术问题是，针对现有数值仿真技术的不足，提供一种计及换相重叠角变化的静止变频器(sfc)负载换相起动数值仿真方法，以满足理论分析及现场事故定位的需求。

为实现上述目的，本发明所采用的方法为：

一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法，包括以下步骤：

步骤一，设静止变频器运行于恒直流电流模式，根据定子电流电角度随时间的变化和换相重叠角，得到定子a相电流与定子电流电角度之间的关系；

步骤二，设静止变频器运行过程中仅计及基波分量的影响，利用park方程得到转子电流、阻尼绕组电流和转速的微分方程组；

步骤三，使用四阶龙格库塔法进行微分方程组计算，得到转子电流、阻尼绕组电流和转速；

步骤四，根据步骤三得到的结果，对机端电压波形补偿由定子电流换相引起的压降，计算得到光滑的机端电压；

步骤五，以每两个机端电压过零点间为正弦波，取光滑的机端电压正弦波的绝对值的最大值作为两个过零点间的峰值并用于步骤三中下一次换相重叠角的迭代计算；

步骤六，检测当前经过的时间是否达到预设时间，如是，则结束整个仿真过程，否则返回步骤三循环迭代执行。

所述的一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法，所述的步骤一中，定子a相电流ia与θ之间的关系通过以下各式表达：

(1)当0≤ωt＜μ：

ia＝ik[cos(γ-ωt)-cosγ)]

(2)当

ia＝id

(3)当

(4)当

ia＝0

(5)当π≤ωt＜π+μ：

ia＝-ik[cos(γ-(ωt-π))-cosγ)]

(6)当

ia＝-id

(7)当

ia＝-[id-ik[cos(γ-(ωt-π))-cosγ)]]

(8)当

ia＝0

其中，θ为定子电流电角度，θ＝ωt，ω为转子机械角速度，t为时间，μ为换相重叠角，ia为定子a相电流，id为整流器输出直流电流，ik为换相过程临时变量，γ为触发超前角。

所述的一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法，所述的步骤二中，转子电流、阻尼绕组电流和转速的微分方程组为下式：

其中，lffd为转子自感，lad为定子d轴电枢反应电感，ld为定子d轴阻尼同步电感，lq为定子q轴阻尼同步电感，if为转子电流，id为d轴阻尼电流，iq为q轴阻尼电流，ω为转子机械角速度，rfd为转子电阻，rd为d轴阻尼绕组电阻，rq为q轴阻尼绕组电阻，lad为定子d轴电枢反应电感，tj为轴系惯性时间常数，laq为定子q轴电枢反应电感，uf为转子电压，ld为定子d轴同步电感，lq为定子q轴同步电感，kw1为转子摩擦系数。

所述的一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法，所述的步骤四中，不考虑换相过程中定子电流的导数项对定子电压的影响，并通过下式计算各平滑电压：

ud_modified＝ra*ids-ω*(laq*iq+lq*iqs)

uq_modified＝ra*iqs+ω*(ld*ids+lad*ifd+lad*id)

ua_modified＝ud_modified*cos(θ_park)-uq_modified*sin(θ_park)

其中ud_modified为ud平滑电压，uq_modified为uq平滑电压，ua_modified为ua平滑电压，laq为定子q轴电枢反应电感，lq为定子q轴同步电感，ld为定子d轴同步电感，lad为定子d轴电枢反应电感。

所述的一种计及换相重叠角变化的静止变频器负载换相起动数值仿真方法，所述的步骤五中，计算中采用ua电压过零点间的瞬时最大值，换相重叠角μ计算过程为：

本发明的技术效果在于，提出了一种计及换相重叠角变化的静止变频器(sfc)负载换相起动数值仿真方法，计及仿真过程中因为机端电压变化导致的换相重叠角变化，消除仿真流程中的矛盾，有效地提高仿真精度，以满足理论分析及现场事故定位的需求。

附图说明

图1为本发明实施总体流程图；

图2为本发明实施数值计算流程图；

图3为考虑换相重叠角μ变化时仿真曲线(μ初始值合适)；

图4为考虑换相重叠角μ变化时仿真曲线(μ初始值不合适)；

图5为不考虑换相重叠角μ变化时仿真曲线(μ初始值合适)；

图6为不考虑换相重叠角μ变化时仿真曲线(μ初始值不合适)。

具体实施方式

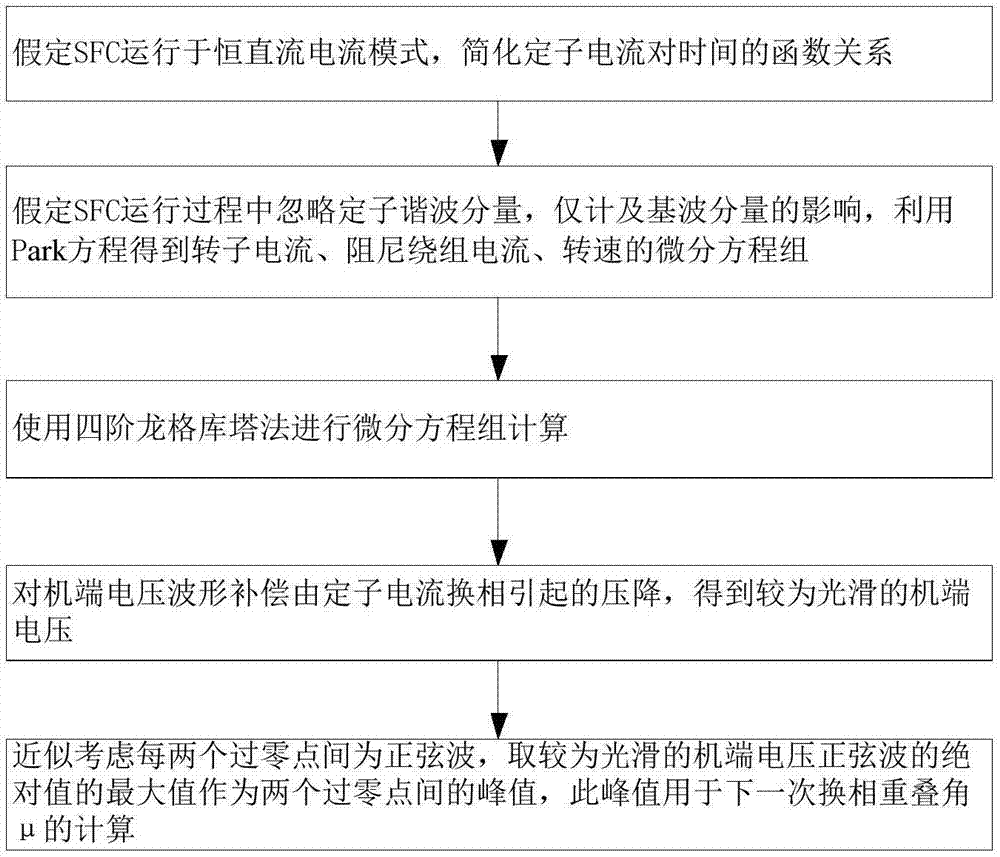
如图1所示，本发明所述的一种计及换相重叠角变化的静止变频器(sfc)负载换相起动数值仿真方法，包括以下步骤：

a假定sfc运行于恒直流电流模式，简化定子电流对时间的函数关系。取θ＝ωt，其中θ为定子电流电角度，设定初始值为0。在θ变化的过程中，假设定子a相电流ia与θ存在关系如式3～10。

(1)0≤ωt＜μ:

ia＝ik[cos(γ-ωt)-cosγ)](式3)

(2)

ia＝id(式4)

(3)

(4)

ia＝0(式6)

(5)π≤ωt＜π+μ

ia＝-ik[cos(γ-(ωt-π))-cosγ)](式7)

(6)

ia＝-id(式8)

(7)

ia＝-[id-ik[cos(γ-(ωt-π))-cosγ)]](式9)

(8)

ia＝0(式10)

b假定sfc运行过程中忽略定子谐波分量，仅计及基波分量的影响，利用park方程得到转子电流、阻尼绕组电流、转速的微分方程组见式11。

c使用四阶龙格库塔法进行微分方程组计算。

d对机端电压波形补偿由定子电流换相引起的压降，得到较为光滑的机端电压。由于换相过程中，定子电流导数项虽然能反应真实的情况，但是会引入定子电压上的毛刺，为了计算换相重叠角μ方便，相当于不考虑定子电流变化导致的电压变化，计算按式12，式13，式14进行：

ud_modified＝ra*ids-ω*(laq*iq+lq*iqs)(式12)

uq_modified＝ra*iqs+ω*(ld*ids+lad*ifd+lad*id)(式13)

ua_modified＝ud_modified*cos(θ_park)-uq_modified*sin(θ_park)(式14)

e近似考虑每两个机端电压过零点间为正弦波，取较为光滑的机端电压正弦波ua_modified的绝对值的最大值作为两个过零点间的峰值，此峰值用于下一次换相重叠角μ的计算，ua电压过零点间的瞬时最大值即为ua_modified中的最大值，计算时机为两个ua过零点间。计算按式15，式16进行。

f检测当前经过的时间是否达到预设时间，如是，则结束整个仿真过程，否则返回步骤c循环迭代执行。如设定仿真时间为10秒，则达到此时间后结束整个仿真过程。

实施例：

构建一台采用静止变频器(sfc)进行起动的同步电机，其运行于负载换相阶段，电机基本参数及状态参数如表1、表2所示。

表1电机特性参数

表2电机初始状态参数

对考虑换相重叠角μ变换与不考虑考虑换相重叠角μ变化情况进行仿真，数值计算具体流程见图2所示。图3显示结果为初始值合适时μ＝5°，考虑换相重叠角μ变化时仿真曲线；图4显示结果为初始值不合适时μ＝10°，考虑换相重叠角μ变化时仿真曲线，可见te曲线在前面部分有一段对不合适μ值的自适应过程，经过自适应后te波形恢复平稳；图5显示结果为初始值合适时μ＝5°，不考虑换相重叠角μ变化时仿真曲线，其ifd及te波形存在微量的下倾，相较于图3差别较小；图6显示结果为初始值不合适时μ＝10°，不考虑换相重叠角μ变化时仿真曲线，可见各变量均出于不稳定的状态，由于没有良好的自适应能力，最终导致结果的发散。

图3至图6表明，在合适的初始值下，考虑μ值变化与不考虑μ值变化对仿真结果影响不大，当初始值不合适时，不考虑μ值变化将引起较大误差，而考虑μ值变化将得到稳定结果。以上仿真结果表明本专利提出的方法的合理性及有效性。