考虑电位平衡和谐波抑制的三电平牵引逆变器控制方法与流程

本发明涉及三电平牵引逆变器控制领域，尤其是涉及一种考虑电位平衡和谐波抑制的三电平牵引逆变器控制方法。

背景技术：

相比于两电平拓扑结构，二极管钳位型三电平牵引逆变器凭借其控制灵活、输出电压等级高、输出谐波含量低等优势已被广泛应用于高速动车组中，并逐步在地铁车辆应用中得到关注。然而由于其自身拓扑结构的特点，该类逆变器工作时会出现直流侧上下分压电容电压不平衡情况，导致中点电位产生波动，从而引起输出电压发生畸变、谐波含量增大，严重影响逆变器工作性能。因此，三电平牵引逆变器的中点电位平衡控制和谐波抑制一直都是国内外学者的关注的问题，如何兼顾中点电位平衡控制和谐波抑制也是逆变器优化控制研究的难点。

对于三电平牵引逆变器而言，中点电位平衡控制目标是降低直流侧分压电容电压的偏移，减小中点电位波动幅值；谐波抑制的主要目标则是提高输出波形质量，减小其总谐波畸变率。现有方法主要实现了对中点电位平衡控制或谐波抑制的单目标控制，兼顾两者的控制方法还未见文献报道。

目前，效果较好的中点电位平衡控制策略多为基于空间矢量的控制方法。choium、bhata等学者提出通过调节冗余小矢量的作用时间对中点电位进行平衡控制，该方法可实现定性控制，但控制精度不够高且没有从本质上对中点电位波动的产生进行分析。范波、桂石翁等学者则利用基于虚拟空间矢量的调制方法使输出三相电流之和为零从而实现对中点电压的全范围控制，但却无法解决计算中近似处理与累计效应造成的中点电位不平衡。针对谐波抑制问题，基于特定次谐波消除pwm方法得到了广泛关注与应用。该方法通过对开关时刻角的优化选择，达到消除特定次谐波的目的，其核心在于如何求解关于开关时刻角的非线性方程组。传统的数值求解法虽然计算简单、精度较高，但在求解过程中存在对初值选取过分依赖、容易出现不收敛等问题。为此，近年来包括遗传算法、蜂群算法、粒子群算法在内的相关智能算法逐渐得以应用，这些算法流程简单，不需要设置复杂的参数，在非线性函数优化和多目标优化等方面具有较大的优势。

技术实现要素：

本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种考虑中点电位平衡和谐波抑制的三电平牵引逆变器控制方法。

本发明的目的可以通过以下技术方案来实现：

一种考虑电位平衡和谐波抑制的三电平牵引逆变器控制方法，包括以下步骤：

1)根据三电平逆变器工作状态构建三电平逆变器的数学模型；

2)计算电平逆变器输出谐波畸变率；

3)计算三电平逆变器中点电位波动；

4)采用罚函数法建立约束条件，根据谐波畸变率和中点电位波动构建多目标优化模型；

5)采用pso算法对多目标优化模型进行求解，最终获得最优开关角序列。

所述的步骤2)中，电平逆变器输出谐波畸变率fthd的计算式为：

其中，udc为三电平逆变器直流侧电压，ul1分别为负载线电压的基波有效值，αi(i＝1,...,n)为1/4周期内可独立优化控制的第i个开关时刻角，n为1/4周期内可独立优化控制的开关时刻角的数量，k为谐波次数，k为谐波总次数。

所述的步骤3)中，不同矢量作用下中点电位波动δuc的计算式为：

其中，udc为三电平逆变器直流侧电压，kj为中间参量，sm、sj分别为逆变器m相和j相的开关状态，τ为等效电路的动态时间常数，ij为三相电流，t为基本周期，r为每相负载的等效电阻，

所述的步骤4)中，多目标优化模型的目标函数和约束条件分别为：

min:f(x)＝fthd

st:δuc＝0。

所述的步骤5)具体包括以下步骤：

501)初始化三电平牵引逆变器参数后，随机产生开关角序列作为初始粒子，并初始化粒子的位置与速度；

502)根据适应度函数值，获得个体最优和全局最优粒子的位置；

503)更新粒子群中每个粒子的速度和位置；

504)获取每个粒子更新后的适应度函数值，当本步中适应度函数值优于前一步的个体最优解，则将其设为新的个体最优解，当个体最优解优于此前的全局最优解，则将其设为新的全局最优解；

505)当迭代次数达到最大迭代次数时，则继续步骤506)，否则，返回步骤503)；

506)当惩罚项为零时，则输出最优解作为最优开关角序列，否则，返回步骤502)。

与现有技术相比，本发明具有以下优点：

一、本发明对控制对象要求简单，适应性强，本发明提供的设计方法仅要求知道被控对象即三电平逆变器的相应参数，而这些参数可以在从被控对象上直接获取，而不要求对象的状态可观，这从很大程度上放宽了对对象的要求，增强了本发明策略的适用性。

二、本发明在设计控制策略过程中充分考虑到实际应用中三电平逆变器的约束条件，增强了控制策略的实用性，本发明提供的控制策略不仅能够有效抑制输出电流谐波，还能同时最大程度地降低中点电位波动幅值，提高了逆变器运行时的动态与稳态性能，增强了本发明策略的实用性和安全性。

三、本发明无需增加其余器件数量，不增加控制成本，性价比高，易实现，应用方便，具有较高的实际应用价值。

附图说明

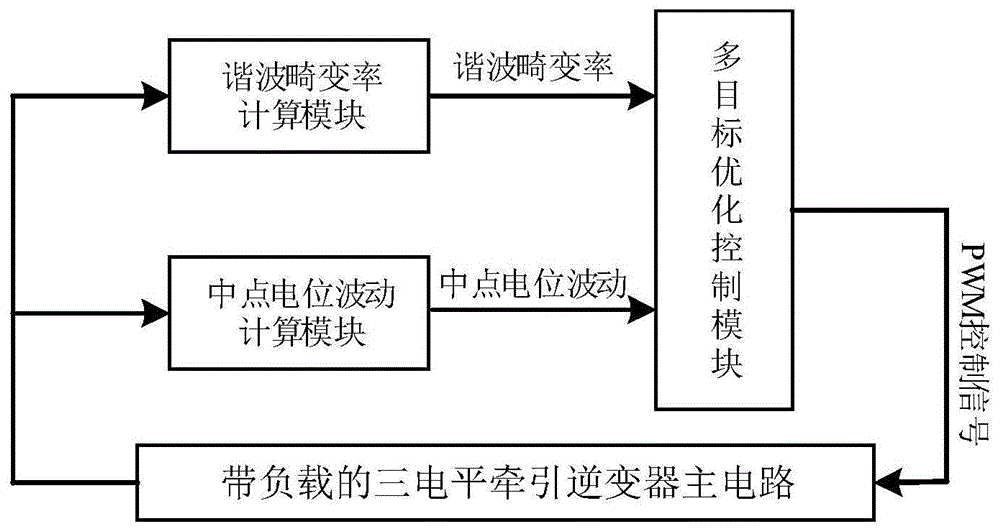
图1为本发明系统结构框图。

图2为三电平逆变器主电路拓扑结构图。

图3为简化前异步电机等效电路图。

图4为简化后异步电机等效电路图。

图5为三电平逆变器电容中点电位波动图。

图6为阻感性负载时三电平逆变器输出相电流波形图。

图7为阻感性负载时三电平逆变器输出相电流频谱图。

图8为阻感性负载时三电平逆变器输出线电压波形图。

图9为阻感性负载时三电平逆变器输出线电压频谱图。

图10为电机负载时三电平逆变器输出相电流波形图。

图11为电机负载时三电平逆变器输出相电流频谱图。

图12为电机负载时三电平逆变器输出线电压波形图。

图13为电机负载时三电平逆变器输出线电压频谱图。

具体实施方式

下面结合附图和具体实施例对本发明进行详细说明。

实施例

如图1所示，本例中提及一种兼顾中点电位平衡控制和谐波抑制的三电平牵引逆变器优化控制系统，该系统主要包括：带负载的三电平牵引逆变器主电路、谐波畸变率计算模块、中点电位波动计算模块、多目标优化控制模块。逆变器主电路输出端连接谐波畸变率计算模块与中点电位波动计算模块，并实时输出开关时刻角序列。谐波畸变率计算模块与中点电位波动计算模块控制器实时计算对应的谐波畸变率以及中点电位波动，并输入至多目标优化控制模块。多目标优化控制模块将优化后的pwm控制信号输出至逆变器主电路，进而控制对应的逆变器工作。

本发明根据控制系统提出一种基于粒子群算法的中点电位平衡控制和谐波抑制多目标优化控制方法，具体包括以下步骤：

1、分析三电平逆变器工作状态，建立其数学模型

图2所示三电平逆变器拓扑中，每相桥臂包含四个功率开关管tj1～tj4(j＝a,b,c)。由分析可知，逆变器每相桥臂四个功率开关管的通断情况决定了此桥臂的开关状态：以a相为例，当sa1、sa2导通且sa3、sa4关断时，桥臂开关状态为“p”；当sa2、sa3导通且sa1、sa4关断时，桥臂开关状态为“o”；当sa3、sa4导通且sa1、sa1关断时，桥臂开关状态为“n”。若定义三电平逆变器每相桥臂的开关状态为sj(j＝a,b,c)，其取值为1、0、-1，则当直流侧电压为udc时，该逆变器的三相桥臂输出相电压可分别为+udc/2、0、-udc/2。

2、建立三电平逆变器输出谐波畸变率计算模型

三电平逆变器控制策略直接影响其输出电压电流的谐波大小。相比于正弦载波pwm、空间矢量pwm调制方法，随机优化pwm调制法可使逆变器输出电压或电流波形谐波含量最低。经过计算，负载电流总谐波畸变率为：

式中，udc为三电平逆变器直流侧电压，il1、ul1分别为负载线电流、线电压的基波有效值，αi(i＝1,...,n)为1/4周期内可独立优化控制的开关时刻角，n为其数量。

由上式(1)可以看出，电流总谐波畸变率由开关时刻角序列x＝[α1,α2,...,αn]决定，对于不同的开关时刻角序列，相应计算得到的电流总谐波畸变率也会不同。

步骤2具体包括以下子步骤：

(201)采用特定次谐波消除pwm方法，可使逆变器输出电压或电流波形谐波含量最低。假设前1/4周期内能够被独立控制的有α1～αn共n个开关时刻角，各个时刻点可按照一定优化目标和优化方法计算得到，则三电平逆变器输出相电压ujn(j＝a,b,c)可表示为：

(202)进一步对相电压进行傅里叶级数展开，且考虑到在三相逆变系统中，输出线电压不含三次及其倍数次的谐波，故可得三电平逆变器输出线电压ul的第k次谐波有效值为：

(203)由于对逆变器供电的大多数负载特别是交流异步电机而言，真正决定和影响系统运行性能的最关键因素为负载电流，故本发明谐波抑制目标变量确定为负载电流总谐波畸变率。异步电机等效电路如图3所示，其中rs为定子电阻，xs为定子的基波电抗，xm为基波互感抗，xr为转子的基波电抗，rr为转子电阻。考虑到谐波次数较高时，其第k次谐波的转差率sk基本接近于1，因此可简化成图4进行分析，由此可得第k次谐波的线电流有效值ilk与线电压有效值ulk之间的关系为：

(204)根据工程应用的要求，计算电压或电流谐波畸变率时最高次谐波取到50次即可，由此可得负载电流总谐波畸变率为：

式中，udc为三电平逆变器直流侧电压，il1、ul1分别为负载线电流、线电压的基波有效值，αi(i＝1,...,n)为1/4周期内可独立优化控制的开关时刻角，n为其数量。

3、建立三电平逆变器中点电位波动计算模型

由上述对三电平逆变器工作原理的分析可知，逆变器每相桥臂开关状态分别取值为“1”、“0”、“-1”时，其对应的输出状态分别为“p”、“o”、“n”，相应的桥臂输出相电压则逆变器共可输出3³＝27种状态，每种状态对应一种电压矢量。按照其对中点电流inp的影响可将电压矢量分成如表1所示的五种类型。

表1矢量分类

可得在不同矢量作用下三相电流为：

式中

由上述各式，最终可得不同矢量作用下中点电位波动为：

式中，τ、r分别为不同矢量作用时对应等效电路的动态时间常数与每相负载的等效电阻，t为基本周期大小。

步骤3包括如下子步骤：

(301)在图2所示主电路中，假设c1＝c2＝c，由基尔霍夫电流定律可得：

由此可得中点电位波动δuc的瞬时表达式为：

(302)假设三相电压矢量可分别取值为1，0，-1，由此可归纳出不同电压矢量作用下中点电流inp与a、b、c三相电流ij(j＝a,b,c)之间的关系为：

其中，sj＝1,0,-1。

通过对不同矢量作用下等效电路进行分析，可得在不同矢量作用下三相电流为：

式中

(303)综合(2)(3)(4)式，最终可得不同矢量作用下中点电位波动δuc为：

式中，τ、r分别为不同矢量作用时对应等效电路的动态时间常数与每相负载的等效电阻，t为基本周期大小。

(304)由式(5)可见，中点电位波动幅值的大小也与开关时刻角序列x＝[α1,α2,...,αn]有关，在逆变器实际运行过程中，任意时刻t的δuc计算过程为：

(3041)根据当前时刻t的开关时刻角序列x的各个开关时刻值得到逆变器三相开关状态sj(j＝a,b,c)，及对应的电压矢量；

(3042)读取上一时刻逆变器的三相电流值ij(t-1)，将其赋给ij(0⁺)(j＝a,b,c)；基于此并结合当前电压矢量，根据上式(4)计算当前时刻三相电流值ij(t)(j＝a,b,c)，并保存；

(3043)根据上式(5)计算一个周期t内总的电压波动δuc的幅值大小。

(4)根据三电平逆变器输出谐波畸变率和中点电位波动数学模型，使用罚函数法建立约束条件，构建多目标优化模型。

本步骤中罚函数法的基本思路是对违反约束条件的非可行点或者试图穿越边界而逃离可行域的点给予惩罚，使其靠近可行域。其构造思想是将约束函数进行组合组成一个“惩罚”项，加在原来的目标函数上以迫使迭代点逼近可行域，由此将约束优化问题变为无约束问题来求解处理。

对于有约束的多目标优化问题，一般可以定义为：

min:f(x)＝(f1(x),f2(x),...,fm(x))

式中，x＝(x1,x2,...,xn)∈r为n维决策变量；f(x)＝(f1(x),f2(x),...,fm(x))是目标函数，包含一个或者多个目标函数；g(x)、h(x)分别为不等式约束条件和等式约束条件。

由于不等式约束条件可以与等式约束条件互相转换，因此，带罚函数的新目标函数可表示为：

min:f(x,m)＝f(x)+ma(x)

式中，m(m>1)为罚因子，为罚函数，ma(x)为惩罚项。

根据罚函数相关定理可知，对于某个确定的m，根据上述优化方法最终求解得到的新目标函数f(x,m)的最优解即为原目标函数f(x)的最优解。

因此，本发明兼顾中点电位平衡控制和谐波抑制的三电平牵引逆变器优化模型即转变为对目标函数min:f(x,m)＝fthd+mδuc进行求解。

(5)根据给定参数，使用pso算法求解多目标优化模型，得到最优开关角序列x＝[α1,α2,...,αn]。

本步骤中使用pso算法求解多目标优化模型具体包括以下几步骤：

(501)逆变器参数初始化后，随机产生开关角序列，并初始化粒子的位置与速度；

(502)计算其适应度函数值，找出个体最优和全局最优位置；

(503)更新粒子的速度和位置；

(504)计算每个粒子更新后的适应度函数值，若此时适应度函数值优于此前的个体最优解，则将其设为新的个体最优解，若个体最优解优于此前的全局最优解，则将其设为新的全局最优解。

(505)如果迭代次数达到最大迭代次数，则继续下一步，否则，返回(503)；

(506)如果惩罚项为零，则输出最优解，否则，返回(502)；

(6)以上海地铁二号线某型车的实际参数为例，搭建了三电平逆变器仿真模型，相应参数设置为：逆变器功率190kw，功率因数0.86，直流侧输入电压udc＝1500v，调制比m＝0.72；pso算法中，初始种群个数n＝40，最大迭代次数maxgen＝50，权重因子w1＝0.7982，w2＝0.2，学习因子c1＝c2＝1.4995；开关时刻角初始序列为：

xi＝[0.57711.04371.16431.54661.55951.56501.56871.5695](rad)

下面就分阻感性负载和电机负载两种情况来说明本发明的有效性。

(601)阻感性负载：假设负载的电阻r＝8.64ω，电感l＝15.9mh，经过寻优计算后得到的开关时刻角为：xi＝[0.29041.49211.52841.53931.55551.55681.56381.5696](rad)，相应的逆变器输入侧电容中点电位波动及逆变器输出电压、电流波形图和频谱分布情况分别如图5～图9所示。

由图5可知，电容电压波峰值为6.7v，波动系数εup＝0.89％；波谷值为-5.8v，波动系数εdown＝0.83％，波动幅值在0v左右上下波动，总波动系数εtotal＝1.72％，由此表明本发明所提优化控制策略的有效性。

由图6-9可知，三电平逆变器输出相电流基频分量幅值为75.11a，thd为1.87％；输出线电压基频分量幅值为1053v，thd为19.23％；谐波主要集中在7、11、13和19次。由此可见，本发明的控制策略能在较低的开关频率下寻优得到更好的开关时刻角，很好地提高和改善了电压、电流利用率和质量。

(602)电机负载：假设星型连接的异步牵引电机负载的参数为：额定电压为1050v，额定电流为132a，额定转速为1500r/min，额定功率为190kw，额定频率为50hz，功率因数为0.85，极对数为4，定子漏感0.001511h，转子漏感为0.001511h，定子转子互感为0.04503h，定子电阻为0.111ω，转子电阻为0.099ω，电机控制方式采用开环控制。经过寻优计算后得到的开关时刻角序列xi与上述阻感性负载相同，由此而得相应的逆变器输出电压、电流波形图和频谱分布情况分别如图10、11、12、13所示。

由图10-图13可见，电机负载时逆变器输出电流基频分量幅值为64.69a，thd为2.09％；输出电压基频分量幅值为1022v，thd为23.72％；谐波主要集中在5、13、17、19次。逆变器输出电压、电流的谐波含量均略高于阻感负载下的相应值，这主要是由于开环电机控制等方式所导致，但基于优化控制策略的逆变器输出信号谐波含量总体均优于传统控制策略。