考虑高耗能点负荷的输电网励磁系统调差系数优化整定方法与流程

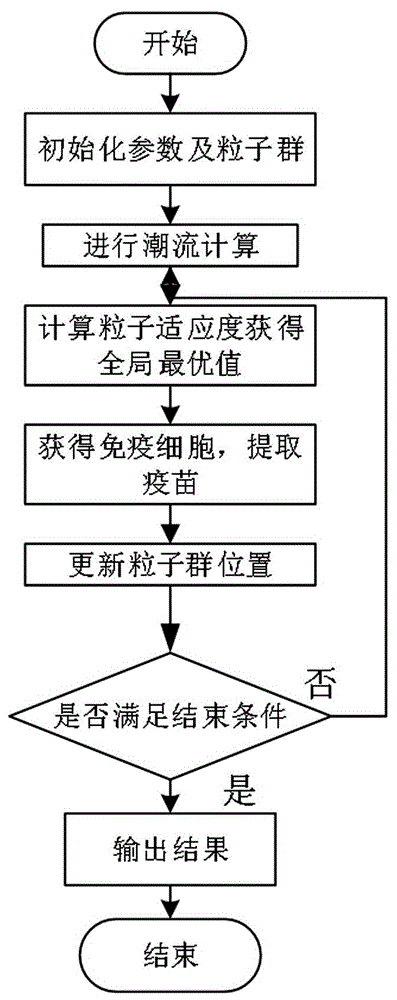
本发明属于电网无功优化控制领域，特别涉及一种考虑高耗能点负荷的输电网励磁系统调差系数优化整定方法。
背景技术：
：随着国家经济和工业的迅速发展，电网用电侧出现了越来越多的单点大功率运行负荷，例如工厂，冶金厂等，这些高耗能点负荷的功率波动对电网运行的影响非常大，严重时会导致电压超出安全范围，甚至引起电机脱网。目前很多地区的电网并没有充分发挥机组的一次调节能力，同时不利于网内功率电压变量波动的稳定，因此需要考虑一次调差来充分发挥机组的调节能力。通过调整调差系数可以控制发电机无功输出对于电压波动的灵敏程度，提高发电机无功输出的能力、降低电力系统网损或对并列发电机组间的无功进行合理分配。现有的励磁系统调差系数研究多考虑全网网损及电压波动建立多目标或考虑供电侧不同发电情况对发电机组调差系数进行整定，并未考虑发电机励磁系统调差系数整定对分层分区后电网负荷侧发生波动的影响。技术实现要素：针对上述现有技术中存在的不足之处，本发明提出了一种考虑高耗能点负荷的输电网励磁系统调差系数优化整定方法，其目的是为了通过输电网励磁系统调差系数优化整定，来减缓负荷侧接入高耗能点负荷对电网的影响。为了实现上述发明目的，本发明是通过以下技术方案来实现的：考虑高耗能点负荷的输电网励磁系统调差系数优化整定方法，包括以下步骤：步骤(1)：建立考虑发电机励磁系统调差系数的电网潮流等效模型；步骤(2)：确定潮流约束方程；步骤(3)：确定考虑点负荷波动的励磁系统调差系数优化模型的目标函数；步骤(4)：由于粒子群在后期易陷入局部最优解，因此对粒子群算法进行改进，将权重系数由常数改为线性递减，由免疫算法启发，在粒子群求解的迭代过程中，将较好的前n个解保存下来作为最优值，对种群进行注射，更新种群中的粒子类型，增大种群找到最优解的可能；利用改进权重与免疫算法结合的粒子群算法，得到发电组对应的励磁调差系数以及电网优化结果。所述建立考虑发电机励磁系统调差系数的电网潮流等效模型，是以“分层分区，就地平衡”为原则，采用模糊聚类的方法对地区电网进行分区，每个区域以区域内无功/电压灵敏度为判断指标选择一个中枢节点；电力系统潮流模型中加入了调差系数β的整定时，参与调差的发电机节点由pv节点变为pβ节点，对于每个节点的调差系数有：其中，uiref为发电机高压侧电压设定参考值；ui为发电机高压侧电压；qiref为发电机输出无功功率设定参考值；qg为发电机输出无功功率。所述步骤(2)确定潮流约束方程，其等式约束为：式中，pi为除平衡节点其他节点发出的有功功率；qi为pq节点发出的无功功率；βi为发电机节点的调差系数；ui为节点i的电压幅值；uj为节点j的电压幅值；gij和bij为节点i,j之间的电导和电纳；θij为节点i,j之间的电压相角；n为总节点数；r为pq节点数；n-r-1为pβ节点数；控制变量约束为：βmin≤β≤βmax，式中βmin，βmax为发电机励磁调差系数上下限；安全约束条件为：式中，u为母线电压幅值；umin，umax为母线电压幅值上下限；qg为发电机输出的无功功率；qgmin，qgmax为发电机输出无功功率上下限。所述步骤(3)中：建立优化模型的目标函数中包含入中枢节点电压波动指标，是中枢节点电压波动时衡量电网稳定运行的重要指标；中枢节点作为电网区域内的重要电压支撑节点，其波动程度表征了整个区域内电压波动情况，同时需要重点考察高耗能点负荷节点的电压波动对电网的影响，因此将中枢节点和高耗能点负荷节点电压波动的标准差作为评判指标之一；其中，f1为关键节点电压波动指标；n为区域内中枢点的个数；uj为第j个中枢节点的运行电压；为第j个中枢节点电压的平均值；ui为高耗能点负荷的运行电压；为高耗能点负荷节点电压平均值；电网的有功网损：f2＝ploss；多目标函数为：minf＝w1f1+w2f2；其中w1、w2分别为电压波动和有功网损的权重系数，权重系数的大小表示各指标对目标函数的影响程度。所述系统为ieee39节点系统时，有10个发电机节点，29个负荷节点；对ieee39节点系统的10台发电机励磁系统进行调差系数优化整定，优化过程包括以下步骤：步骤1：以“分层分区，就地平衡”为原则，采用模糊聚类的方法对39节点系统进行分区，每个区域内选择一个中枢节点，分别是1,12,16,20,28节点；步骤2：将控制变量调差系数β加入matpower中39节点系统潮流计算，设定β的范围为[0,0.6]，求解含励磁调差系数的电网潮流计算；当潮流有解时，则满足等式约束及不等式约束；步骤3：结合建立的多目标函数，在ieee39节点系统负荷节点中任选取1个负荷节点，同时增大或缩小其负荷功率，来模拟实际工业中某些高耗能点负荷接入电网造成的影响；步骤4：随机生成一组调差系数值进行电网潮流进行计算，对有功网损和中枢节点电压波动指标进行加权得到目标函数，利用改进的粒子群算法进行迭代循环求解，最终可得到目标函数最优解以及相应的机组调差系数值。所述节点是以节点4为例，将其负荷增大2.5倍，缩小0.4倍进行潮流计算和调差系数的优化整定，得到优化前后点负荷母线电压变化，网损及电压波动值。所述节点中的节点4点负荷波动对应优化结果如下：当点负荷出现重载时，点负荷电压已经超出电压波动的安全范围，此时会对电网运行造成非常不利的影响，增加调差系数优化控制，使点负荷在重载时电压能够回到在安全范围内，同时网损以及电压波动均有明显改善，轻载时网损有明显降低，虽然电压波动略有增加，但幅度较小，在可接受范围。所述调差系数，是通过增加和减小负载时发电机组来对应调差系数；重载时发电机励磁调差系数普遍大于轻载，对励磁调差系数进行整定对重载即高耗能点负荷接入电网更为必要；由于0.4倍负载和2.5倍负载分别对应一组调差系数，而实际应用中发电机组调差系数一般不轻易变动，因此将采用专家评估统计法对两组调差数据进行处理，得0.4倍和2.5倍负载对应的权重系数分别为：0.25,0.75，则最终得到发电机组的调差系数；结合最终整定得调差系数值计算潮流得到点负荷波动固定调差系数对应优化结果；经固定调差系数优化后，重载时负荷节点电压越限情况消除，关键节点的电压幅值均有增大，同时优化后电网网损均下降，此时轻载时电压波动略有上升，对发电机组进行励磁调差系数优化整定对有高耗能点负荷的电网有利。本发明首先以“分层分区，就地平衡”为原则，采用模糊聚类的方法对地区电网进行分区，选出中枢节点。然后建立考虑发电机励磁系统调差系数的电网潮流等效模型，以网损和中枢节点及高耗能点负荷电压波动的多目标函数，电网潮流为约束，对励磁调差系数进行整定，采用改进权重与免疫算法结合的粒子群算法进行求解，得到发电机的励磁调差系数及优化前后关键节点电压变化，网损及电压波动值。本发明建立了考虑高耗能点负荷的输电网励磁系统调差系数优化整定模型，弥补了发电机励磁系统调差系数在负荷侧波动方面研究的空白。另外，经过多目标优化后，高耗能点负荷节点电压升高，可避免节点发生低压越限的情况，同时有效降低全网网损，提高了电网运行的经济性和可靠性。附图说明为了便于本领域普通技术人员理解和实施本发明，下面结合附图及具体实施方式对本发明作进一步的详细描述，但应当理解本发明的保护范围并不受具体实施方式的限制。图1为本发明考虑高耗能点负荷的输电网励磁系统调差系数优化整定模型算法流程图。图2为ieee39节点结构及分区图。图3为负荷波动对应的调差系数图。图4为优化前后重载时关键节点电压对比图。图5为优化前后轻载时关键节点电压对比图。具体实施方式本发明是一种考虑高耗能点负荷的输电网励磁系统调差系数优化整定方法，包括以下步骤：(1)建立考虑发电机励磁系统调差系数的电网潮流等效模型；(2)确定潮流约束方程；(3)确定考虑点负荷波动的励磁系统调差系数优化模型的目标函数；(4)由于粒子群在后期易陷入局部最优解，因此对粒子群算法进行改进，将权重系数由常数改为线性递减，由免疫算法启发，在粒子群求解的迭代过程中，将较好的前n个解保存下来作为最优值，对种群进行注射，更新种群中的粒子类型，增大种群找到最优解的可能；利用改进权重与免疫算法结合的粒子群算法，得到发电组对应的励磁调差系数以及电网优化结果。所述步骤(1)建立考虑发电机励磁系统调差系数的电网潮流等效模型，是以“分层分区，就地平衡”为原则，采用模糊聚类的方法对地区电网进行分区，每个区域以区域内无功/电压灵敏度为判断指标选择一个中枢节点；电力系统潮流模型中加入了调差系数β的整定时，参与调差的发电机节点由pv节点变为pβ节点，对于每个节点的调差系数有：其中，uiref为发电机高压侧电压设定参考值；ui为发电机高压侧电压；qiref为发电机输出无功功率设定参考值；qg为发电机输出无功功率。所述步骤(2)确定潮流约束方程，其等式约束为：式中，pi为除平衡节点其他节点发出的有功功率；qi为pq节点发出的无功功率；βi为发电机节点的调差系数；ui为节点i的电压幅值；uj为节点j的电压幅值；gij和bij为节点i,j之间的电导和电纳；θij为节点i,j之间的电压相角；n为总节点数；r为pq节点数；n-r-1为pβ节点数；控制变量约束为：βmin≤β≤βmax，式中βmin，βmax为发电机励磁调差系数上下限；安全约束条件为：式中，u为母线电压幅值；umin，umax为母线电压幅值上下限；qg为发电机输出的无功功率；qgmin，qgmax为发电机输出无功功率上下限。所述所述步骤(3)中：优化模型的目标函数包含入中枢节点电压波动指标，是中枢节点电压波动时衡量电网稳定运行的重要指标)中枢节点作为电网区域内的重要电压支撑节点，其波动程度表征了整个区域内电压波动情况，同时需要重点考察高耗能点负荷节点的电压波动对电网的影响，因此将中枢节点和高耗能点负荷节点电压波动的标准差作为评判指标之一：其中，f1为关键节点电压波动指标；n为区域内中枢点的个数；uj为第j个中枢节点的运行电压；为第j个中枢节点电压的平均值；ui为高耗能点负荷的运行电压；为高耗能点负荷节点电压平均值；电网的有功网损：f2＝ploss；其中ploss为电网运行过程中的有功损耗；多目标函数为：minf＝w1f1+w2f2；其中w1、w2分别为电压波动和有功网损的权重系数，权重系数的大小表示各指标对目标函数的影响程度。f为优化总目标；f1为关键节点电压波动指标；f2为电网有功损耗指标。实施例1：本发明以ieee39节点系统为例，该系统中有10个发电机节点，29个负荷节点；对ieee39节点系统的10台发电机励磁系统进行调差系数优化整定，优化过程如下：步骤1：以“分层分区，就地平衡”为原则，采用模糊聚类的方法对39节点系统进行分区，每个区域内选择一个中枢节点，分别是1,12,16,20,28节点。系统结构图以及分区情况见图2所示。步骤2：将控制变量调差系数β加入matpower中39节点系统潮流计算，设定β的范围为[0,0.6]，求解含励磁调差系数的电网潮流计算；当潮流有解时，则满足等式约束及不等式约束。步骤3：结合本发明建立的多目标函数，在ieee39节点系统负荷节点中任选取1个负荷节点，同时增大或缩小其负荷功率，来模拟实际工业中某些高耗能点负荷接入电网造成的影响。步骤4：随机生成一组调差系数值进行电网潮流进行计算，对有功网损和中枢节点电压波动指标进行加权得到目标函数，利用改进的粒子群算法进行迭代循环求解，最终可得到目标函数最优解以及相应的机组调差系数值。算法流程图见图1，得到优化结果。以节点4为例，将其负荷增大2.5倍，缩小0.4倍进行潮流计算和调差系数的优化整定，得到优化前后点负荷母线电压变化，网损及电压波动值。由表1可见，表1是4节点点负荷波动对应优化结果。当点负荷出现重载时，点负荷电压已经超出电压波动的安全范围，此时会对电网运行造成非常不利的影响，增加调差系数优化控制，使点负荷在重载时电压能够回到在安全范围内，同时网损以及电压波动均有明显改善，轻载时网损有明显降低，虽然电压波动略有增加，但幅度较小，在可接受范围，总的来说增加调差系数整定时很有必要的。增加和减小负载时发电机组对应调差系数见图3；由图3可看出重载时发电机励磁调差系数普遍大于轻载。这说明对励磁调差系数进行整定对重载即高耗能点负荷接入电网更为必要，进一步验证了本发明的结论。由于0.4倍负载和2.5倍负载分别对应一组调差系数，而实际应用中发电机组调差系数一般不轻易变动，因此将采用专家评估统计法对两组调差数据进行处理，得0.4倍和2.5倍负载对应的权重系数分别为：0.25,0.75。则最终得到发电机组的调差系数见表2所示。结合最终整定得调差系数值计算潮流得到结果见表3和图4，表3是点负荷波动固定调差系数对应优化结果。由表3和图4可得，经固定调差系数优化后，重载时负荷节点电压越限情况消除，关键节点的电压幅值均有一定程度的增大，说明这种控制策略对电网电压有提升作用。同时优化后电网网损均下降，但此时轻载时电压波动略有上升，如图5所示，但综合考虑认为对发电机组进行励磁调差系数优化整定对有高耗能点负荷的电网还是很有利的。本发明应用具体事例对本发明进行了阐述，值得提出的是，这并非对本发明的限制，而是用于帮助理解本发明的方法和中心思想。相关领域的技术人员在保持发明的精神的状态下，基于此方案做出的变化和变型及应用范围的改变均属于本发明的范畴。表1.4节点点负荷波动对应优化结果ploadβv4/p.uploss/mwδv/p.u2.5*pload400.93357.750.0802.5*pload4β40.95455.460.0810.4*pload401.02342.120.0780.4*pload4β41.02941.760.091表2发电机组调差系数整定值发电机β410.053320.06030.04540.031650.06060.06070.06080.045990.0545100.0454表3点负荷波动固定调差系数对应优化结果ploadβv4/p.uploss/mwδv/p.u2.5*pload400.93357.750.0802.5*pload4β40.95455.460.0800.4*pload401.02342.120.0780.4*pload4β41.03841.290.097当前第1页12