基于状态约束的异步电动机命令滤波模糊控制方法与流程

本发明属于异步电动机位置跟踪控制技术领域，尤其涉及一种考虑铁损的基于状态约束的异步电动机命令滤波模糊控制方法。

背景技术：

异步电动机因其廉价、结构简单、可靠性高以及耐用的优点，在工业、农业、航天等领域得到了广泛的应用。异步电动机的数学模型具有高阶非线性和参数时变的特性，传统的矢量控制和直接转矩控制方法难以获得良好的动态响应。近年来，自适应控制、模糊控制和反步控制等先进的控制方法被广泛应用于异步电动机驱动系统的相关问题研究中。其中，基于模糊逻辑的自适应控制方法可用来逼近系统中的非线性函数；而反步法作为最有效的构建控制器的方法之一，引起了越来越多的关注。然而，当需要对虚拟控制函数重复求导时，传统反步法会出现“计算爆炸”的问题。在许多实际工程中，系统的输出和状态总是被约束在给定的区间内，否则将不能保证安全规范和系统的性能。另外，违反状态约束可能使系统的性能退化，出现故障，甚至威胁人身安全。当异步电动机实际应用(如吊车、机床等)时，转子位置和转子角速度都应被限制在给定的范围内。过大的转子磁链会导致转子磁芯的饱和，产生严重的热损耗。过大的励磁电流会造成电网的电压波动，并会影响同一电网其他设备的操作。同时，电机绕组严重发热，会加速绝缘老化，缩短电机使用寿命。因此，对于异步电动机来说，转子位置、转子角速度、转子磁链和励磁电流等状态量都应被限制在一定的范围内。此外，长时间工作在轻载状态下，异步电动机将产生大量的铁芯损耗，这将对控制性能产生不利的影响。由此可见，迫切需要提出一种控制方法，以解决上述技术问题。

技术实现要素：

本发明的目的在于提出一种基于状态约束的异步电动机命令滤波模糊控制方法，以克服传统反步法引起的计算爆炸问题，且保证异步电动机驱动系统的状态量在给定的状态区间内。

本发明为了实现上述目的，采用如下技术方案：

基于状态约束的异步电动机命令滤波模糊控制方法，包括如下步骤：

a.建立考虑铁损的异步电动机的动态数学模型，如公式(1)所示：

其中，θ为转子角度，ωr为转子角速度，j为转动惯量，tl为负载转矩，ψd为转子磁链，np为极对数，ids为d轴定子电流，iqs为q轴定子电流，idm为d轴励磁电流，iqm为q轴励磁电流，uds为d轴定子电压，uqs为q轴定子电压，rs为定子的电阻，l1s为定子的电感，rr为转子的电阻，l1r为转子的电感，rfe为铁损阻抗，lm为互感；

为了简化上述动态数学模型，定义如下新变量：

则考虑铁损的异步电动机的动态数学模型表示为：

b.采用barrierlyapunov函数，设计一种考虑铁损的基于状态约束的异步电动机命令滤波模糊控制方法，控制目标是设计电压uds和uqs为真实控制律，使得x1和x5分别跟踪期望的位置信号x1d和x5d，同时使异步电动机驱动系统的状态量始终在给定的区间内；

命令滤波器定义如下：

其中，均为命令滤波器的输出信号，ic＝1,2,3,4,5；α1为命令滤波器的输入信号；如果命令滤波器的输入信号α1在t≥0时满足：和其中，ρ1和ρ2均为正数，且在t＝0满足则对于任意的μ＞0，存在ωn＞0，使得和都是稳定的；

假设f(z)在紧集ωz中是一个连续的函数，对于任意的常数ε＞0，总存在一个模糊逻辑系统w^ts(z)满足：式中，输入向量q是模糊输入维数，r^q为实数向量集；w∈r^l是模糊权向量，模糊节点数l为正整数，且l＞1，r^l为实数向量集；s(z)＝[s1(z),...,sl(z)]^t∈r^l为基函数向量，s1(z),...,sl(z)分别表示s(z)的基函数；

选取基函数si(z)为如下的高斯函数：

其中，μi＝[μi1,...,μiq]^t是gaussian函数分布曲线的中心位置，ηi为gaussian函数宽度；

μi1,...,μiq为μi的基向量；

定义跟踪误差变量为：

其中，x1d和x5d为期望的位置信号，虚拟控制律α1，α2，α3，α4，α5为命令滤波器的输入信号，x1,c、x2,c、x3,c、x4,c、x5,c为对应命令滤波器的输出信号；

定义如下两个紧集：

为正常数；为正常数；

其中，y0、y1、y2、y3为正常数；

定义滤波误差补偿信号：ξie＝zie-vie，vie为补偿后的误差，其中，ie＝1,2,…,7；

控制方法设计的每一步都会采用一个barrierlyapunov函数来构建一个虚拟控制律或者真实的控制律，控制方法具体包括以下步骤：

b1.对于期望的位置信号x1d，选取barrierlyapunov函数为：

对v1求导得：

其中，选取虚拟控制律α1和滤波误差补偿信号的导数即：

其中，k1为大于0的常数，将公式(6)和公式(7)代入公式(5)，得到：

b2.选取barrierlyapunov函数为：

对v2求导得到：

其中，

在实际应用中负载转矩tl为有限值，设定tl的上限为d，且d＞0，则有0≤|tl|≤d；

利用杨氏不等式得到：ε1为任意小的正数；

公式(10)表示为：

其中，k1为大于0的常数，根据万能逼近定理，对于任意给定的ε2＞0，存在一个模糊逻辑系统使其中，δ2(z)为逼近误差并满足|δ2(z)|≤ε2；由此得到：

其中，l2表示大于0的常数，||w2||为w2的范数；

构造虚拟控制律α2和滤波误差补偿信号的导数即：

其中k2为大于0的常数，为未知常数θ的估计值，将公式(12)～(14)代入公式(11)得到：

b3.选取barrierlyapunov函数为对v3求导后得到：

其中，

根据万能逼近定理，对于任意给定的ε3＞0，存在一个模糊逻辑系统使其中，δ3(z)为逼近误差并满足|δ3(z)|≤ε3；由此得到：

其中，l3为大于0的常数，||w3||为w3的范数；

选取虚拟控制律α3和滤波误差补偿信号的导数

其中，k3为大于0的常数；将公式(17)～(19)代入公式(16)，得到：

b4.选取barrierlyapunov函数为

对v4求导得到：

其中，

根据万能逼近定理，对于任意给定的ε4＞0，存在一个模糊逻辑系统使其中，δ4(z)为逼近误差并满足|δ4(z)|≤ε4；由此得到：

其中，l4为大于0的常数，||w4||为w4的范数；

选取真实控制律uqs和滤波误差补偿信号的导数

其中，k4为大于0的常数；将公式(22)～(24)代入公式(21)，得到：

b5.选取barrierlyapunov函数为：

对公式(26)求导后得到：

其中，构造如下虚拟控制律α4和滤波误差补偿信号的导数

其中，k5为大于0的常数；将公式(28)和公式(29)代入公式(27)，得到：

b6.选取barrierlyapunov函数为

对公式(31)求导后得到：

其中，

根据万能逼近定理，对于任意给定的ε6＞0，存在一个模糊逻辑系统使其中，δ6(z)为逼近误差并满足|δ6(z)|≤ε6；由此得到：

其中，l6为大于0的常数，||w6||为w6的范数；

选取虚拟控制律α5和滤波误差补偿信号的导数

其中，k6为大于0的常数；将公式(33)～(35)代入公式(32)，得到：

b7.设计真实控制律uds，选取障碍lyapunov函数为：

对公式(37)求导后得到：

其中，

根据万能逼近定理，对于任意给定的ε7＞0，存在一个模糊逻辑系统使其中，δ7(z)为逼近误差并满足|δ7(z)|≤ε7；由此得到：

其中，l7为大于0的常数，||w7||为w7的范数；

选取真实控制律uds和滤波误差补偿信号的导数

其中，k7为大于0的常数；定义θ＝max{||w2||²,||w3||²,||w4||²,||w6||²,||w7||²}，并定义θ的估计误差为将公式(39)～(41)代入公式(38)得到：

b8选取整个系统的lyapunov函数：

对v求导后得到：

选取如下自适应律：

其中，r1和m1均为正数；

c.对基于状态约束的异步电动机命令滤波控制方法进行稳定性分析；

将公式(45)代入公式(44)，得到：

由于当时，且运用杨氏不等式得到：则公式(46)转化成如下不等式，即：

其中，

由公式(47)得知，和都是有界的；

在公式(47)两边同时乘以e^at，并在(0,t]内积分得到：

其中，v(t)为李雅普诺夫函数，v(0)表示李雅普诺夫函数的初始状态；

公式(48)表明，且有界；显然

由ξie＝zie-vie得知，zie＝vie+ξie；

为了证明滤波误差补偿信号ξie的有界，设计补偿信号的lyapunov方程为：

对v0求导得到：

其中，

并有由v1＝z1-ξ1，可得：

通过该公式得知，跟踪误差能够趋于零的邻域；

由可知，是有界的；因为v1＝z1-ξ1，所以

同样，因为z1＝x1-x1d且x1d≤y0，所以又因为α1是z1和的函数，所以α1是有界的，设α1满足其中，是一正常数；

然后，由v2＝z2-ξ2可知，|z2|≤|v2|+|ξ2|≤由z2＝x2-x1,c得到：x2＝z2+(x1,c-α1)+α1，

依次得到由于uqs是z4,v4,v3,及的函数，因此uqs是有界的；uds是z7,v7,v6,及的函数，因此uds也是有界的；

综上，系统状态变量被约束在紧集ωx内，以保证异步电动机驱动系统的状态约束要求。

本发明具有如下优点：

(1)本发明构建障碍lyapunov函数，以保证异步电动机驱动系统的转子角速度、定子电流等状态量始终在给定的状态区间内，避免因违反状态约束而引发的安全性问题。

(2)本发明引入命令滤波技术，以克服传统反步法无法避免的“计算爆炸”问题，并引入滤波误差补偿机制消除滤波误差的影响，进而提升系统的控制性能。

(3)本发明利用模糊逻辑系统处理系统中的非线性函数，将命令滤波反步技术与模糊自适应方法结合起来控制异步电动机，实现理想的位置跟踪控制效果。

(4)本发明需要的输入信号是实际工程中易于得到的可直接测量的转速、磁链及电流信号量，模糊自适应算法本身可以通过软件编程实现，易于对异步电动机进行控制。

(5)本发明考虑了异步电动机的铁损问题，使用一个考虑铁损的异步电动机的动态模型，本发明的控制方法将更切合实际。

(6)本发明仅采用一个自适应律，减轻了在线计算负担，易于工程实现。

附图说明

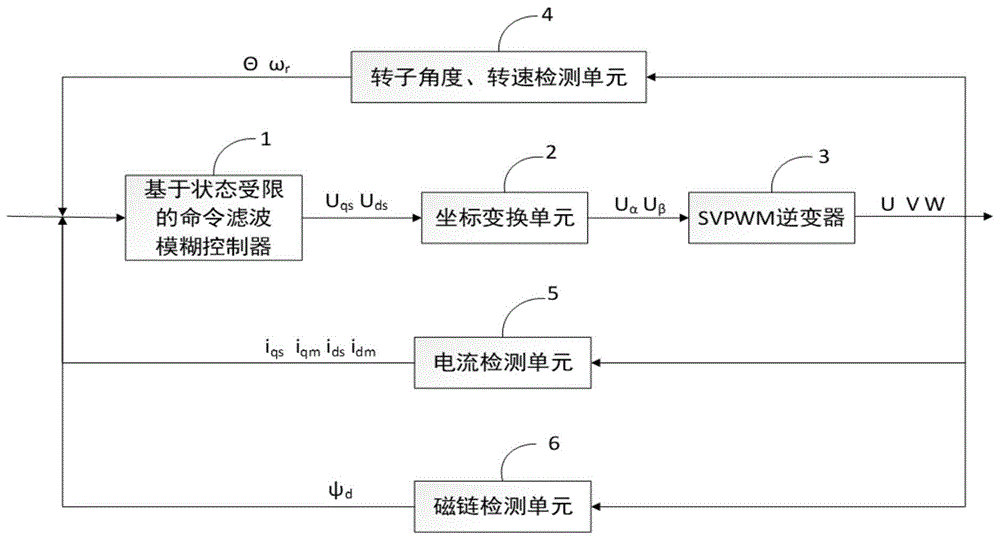
图1是本发明实施例中基于状态约束的命令滤波模糊控制器、坐标变换单元、svpwm逆变器和检测单元组成的复合被控对象的示意图；

图2是采用本发明控制方法后转子角度和转子角度设定值跟踪仿真图；

图3是采用本发明控制方法后转子磁链和转子磁链设定值跟踪仿真图；

图4是采用本发明控制方法后转子角度跟踪误差仿真图；

图5是采用本发明控制方法后转子磁链跟踪误差仿真图；

图6是采用本发明控制方法后异步电动机q轴定子电压仿真图；

图7是采用本发明控制方法后异步电动机d轴定子电压仿真图；

图8是采用本发明控制方法后异步电动机状态x2,x3,x4仿真图；

图9是采用本发明控制方法后异步电动机状态x5,x6,x7仿真图。

具体实施方式

本发明的基本思想为：

利用模糊逻辑系统逼近异步电动机驱动系统中的非线性项，利用障碍lyapunov函数将异步电动机驱动系统的转子角速度、定子电流等状态始终约束在给定的状态区间内。

同时，引入命令滤波技术克服传统反步法无法避免的“计算爆炸”问题，并引入滤波误差补偿机制消除滤波误差的影响，构造了命令滤波模糊位置跟踪控制器。

下面结合附图以及具体实施方式对本发明作进一步详细说明：

如图1所示，基于状态约束的异步电动机命令滤波模糊控制方法，其采用的部件包括：

基于状态约束的命令滤波模糊控制器1、坐标变换单元2、svpwm逆变器3、转子角度和转速检测单元4、电流检测单元5和磁链检测单元6。

其中，u、v、w表示三相电压，uα和uβ为两相静止坐标系下的电压。

转子角度和转速检测单元4、电流检测单元5和磁链检测单元6主要用于检测异步电动机的转子角度和转速、电流值和磁链变量。

通过实际测量的转子角度和转速、电流值和磁链变量作为输入，基于状态约束的命令滤波模糊控制器1进行电压控制，最终转换为三相电控制异步电动机的转子角位置。

为了设计一个更加有效的控制器，建立考虑铁损异步电动机动态模型是十分必要的。

基于状态约束的异步电动机命令滤波模糊控制方法，包括如下步骤：

a.建立考虑铁损的异步电动机的动态数学模型，如公式(1)所示：

其中，θ为转子角度，ωr为转子角速度，j为转动惯量，tl为负载转矩，ψd为转子磁链，np为极对数，ids为d轴定子电流，iqs为q轴定子电流，idm为d轴励磁电流，iqm为q轴励磁电流，uds为d轴定子电压，uqs为q轴定子电压，rs为定子的电阻，l1s为定子的电感，rr为转子的电阻，l1r为转子的电感，rfe为铁损阻抗，lm为互感。

为了简化上述动态数学模型，定义如下新变量：

则考虑铁损的异步电动机的动态数学模型表示为：

b.采用barrierlyapunov函数，设计一种考虑铁损的基于状态约束的异步电动机命令滤波模糊控制方法，控制目标是设计电压uds和uqs为真实控制律，使得x1和x5分别跟踪期望的位置信号x1d和x5d，同时使异步电动机驱动系统的状态量始终在给定的区间内。

命令滤波器定义如下：

其中，均为命令滤波器的输出信号，ic＝1,2,3,4,5，α1为命令滤波器的输入信号；如果命令滤波器的输入信号α1在t≥0时满足：和其中，ρ1和ρ2均为正数，且在t＝0满足则对于任意的μ＞0，存在ωn＞0，使得和都是稳定的。

假设f(z)在紧集ωz中是一个连续的函数，对于任意的常数ε＞0，总存在一个模糊逻辑系统w^ts(z)满足：式中，输入向量q是模糊输入维数，r^q为实数向量集；w∈r^l是模糊权向量，模糊节点数l为正整数，且l＞1，r^l为实数向量集；s(z)＝[s1(z),...,sl(z)]^t∈r^l为基函数向量，s1(z),...,sl(z)分别表示s(z)的基函数。

选取基函数si(z)为如下的高斯函数：

其中，μi＝[μi1,...,μiq]^t是gaussian函数分布曲线的中心位置，ηi为gaussian函数宽度。

μi1,...,μiq为μi的基向量。

定义跟踪误差变量为：

其中，x1d和x5d为期望的位置信号，虚拟控制律α1，α2，α3，α4，α5为命令滤波器的输入信号，x1,c、x2,c、x3,c、x4,c、x5,c为对应命令滤波器的输出信号。

定义如下两个紧集：

为正常数；为正常数。

其中，y0、y1、y2、y3为正常数。

定义滤波误差补偿信号：ξie＝zie-vie，vie为补偿后的误差，其中ie＝1,2,…,7。

虚拟控制律和滤波误差补偿信号的具体结构将在下面的设计过程中给出。

控制方法设计的每一步都会采用一个barrierlyapunov函数来构建一个虚拟控制律或者真实的控制律，控制方法具体包括以下步骤：

b1.对于期望的位置信号x1d，选取barrierlyapunov函数为：

对v1求导得：

其中，选取虚拟控制律α1和滤波误差补偿信号的导数即：

其中，k1为大于0的常数，将公式(6)和公式(7)代入公式(5)，得到：

b2.选取barrierlyapunov函数为：

对v2求导得到：

其中，

在实际应用中负载转矩tl为有限值，设定tl的上限为d，且d＞0，则有0≤|tl|≤d。

利用杨氏不等式得到：ε1为任意小的正数。

公式(10)表示为：

其中，k1为大于0的常数，根据万能逼近定理，对于任意给定的ε2＞0，存在一个模糊逻辑系统使其中，δ2(z)为逼近误差并满足|δ2(z)|≤ε2。由此得到：

其中，l2表示大于0的常数，||w2||为w2的范数。

构造虚拟控制律α2和滤波误差补偿信号的导数即：

其中k2为大于0的常数，为未知常数θ的估计值。将公式(12)～(14)代入公式(11)得到：

b3.选取barrierlyapunov函数为对v3求导后得到：

其中，

根据万能逼近定理，对于任意给定的ε3＞0，存在一个模糊逻辑系统使其中，δ3(z)为逼近误差并满足|δ3(z)|≤ε3。由此得到：

其中，l3为大于0的常数，||w3||为w3的范数。

选取虚拟控制律α3和滤波误差补偿信号的导数

其中，k3为大于0的常数。将公式(17)～(19)代入公式(16)，得到：

b4.选取barrierlyapunov函数为

对v4求导得到：

其中，

根据万能逼近定理，对于任意给定的ε4＞0，存在一个模糊逻辑系统使其中，δ4(z)为逼近误差并满足|δ4(z)|≤ε4。由此得到：

其中，l4为大于0的常数，||w4||为w4的范数。

选取真实控制律uqs和滤波误差补偿信号的导数

其中，k4为大于0的常数。将公式(22)～(24)代入公式(21)，得到：

b5.选取barrierlyapunov函数为：

对公式(26)求导后得到：

其中，构造如下虚拟控制律α4和滤波误差补偿信号的导数

其中，k5为大于0的常数。将公式(28)和公式(29)代入公式(27)，得到：

b6.选取barrierlyapunov函数为

对公式(31)求导后得到：

其中，

根据万能逼近定理，对于任意给定的ε6＞0，存在一个模糊逻辑系统使其中，δ6(z)为逼近误差并满足|δ6(z)|≤ε6。由此得到：

其中，l6为大于0的常数，||w6||为w6的范数。

选取虚拟控制律α5和滤波误差补偿信号的导数

其中，k6为大于0的常数。将公式(33)～(35)代入公式(32)，得到：

b7.设计真实控制律uds，选取障碍lyapunov函数为：

对公式(37)求导后得到：

其中，

根据万能逼近定理，对于任意给定的ε7＞0，存在一个模糊逻辑系统使其中，δ7(z)为逼近误差并满足|δ7(z)|≤ε7。由此得到：

其中，l7为大于0的常数，||w7||为w7的范数。

选取真实控制律uds和滤波误差补偿信号的导数

其中，k7为大于0的常数。定义θ＝max{||w2||²,||w3||²,||w4||²,||w6||²,||w7||²}，并定义θ的估计误差为将公式(39)～(41)代入公式(38)得到：

b8选取整个系统的lyapunov函数：

对v求导后得到：

选取如下自适应律：

其中，r1和m1均为正数。

c.对基于状态约束的异步电动机命令滤波控制方法进行稳定性分析。

将公式(45)代入公式(44)，得到：

由于当时，且运用杨氏不等式得到：

则公式(46)转化成如下不等式，即：

其中，

由公式(47)得知，和都是有界的。

在公式(47)两边同时乘以e^at，并在(0,t]内积分得到：

其中，v(t)为李雅普诺夫函数，v(0)表示李雅普诺夫函数的初始状态。

公式(48)表明，且有界；显然

由ξie＝zie-vie得知，zie＝vie+ξie。

为了证明滤波误差补偿信号ξie的有界，设计补偿信号的lyapunov方程为：

对v0求导得到：

其中，

并有由v1＝z1-ξ1，可得：通过该公式得知，通过选取足够大的a和a0，及足够小的b和b0能够使得跟踪误差趋于零的邻域。

由可知，是有界的。因为v1＝z1-ξ1，所以

同样，因为z1＝x1-x1d且x1d≤y0，所以又因为α1是z1和的函数，所以α1是有界的，设α1满足其中，是一正常数。

然后，由v2＝z2-ξ2可知，由z2＝x2-x1,c可得：x2＝z2+(x1,c-α1)+α1，

依次类推，可知由于uqs是z4,v4,v3,及的函数，所以uqs是有界的。同样，uds是z7,v7,v6,及的函数，所以uds是有界的。

综上，系统状态变量被约束在紧集ωx内，保证了异步电动机系统的状态约束要求。

由以上分析得到在真实控制律uqs和uds的作用下，系统跟踪误差收敛到原点的一个充分小的邻域内，异步电动机驱动系统的状态始终在给定的状态区间内，没有违反状态约束条件。

下面在虚拟环境下对所提出的考虑铁损的基于状态约束的异步电动机命令滤波模糊控制方法进行仿真，以验证所提出控制方法的可行性。

电机及负载参数为：

j＝0.0586kg·m²,rs＝0.1ω,rr＝0.15ω,rfe＝30ω,lm＝0.068h,l1s＝l1r＝0.0699h。

选择控制律参数为：

k1＝8,k2＝8,k3＝20,k4＝1100,k5＝150,k6＝200,k7＝200,r1＝0.05,m1＝0.02。

l2＝l3＝l4＝l6＝l7＝0.25。

命令滤波器参数选取为ζ＝0.5,ωn＝500。

跟踪参考信号为：x1d＝sint；期望转子磁链信号为：x5d＝1。

设负载转矩为

异步电动机仿真初始状态为[0,0,0,0,1,0,0]。

选取

则系统的状态区间为：|x1|≤1.5,|x2|≤35,|x3|≤35,|x4|≤35,|x5|≤1.5,|x6|≤35,|x7|≤35。

模糊隶属度函数为：

其中，ie＝1,2,3,4,5,6,7。

基于状态约束的命令滤波模糊自适应控制方法的仿真结果如附图2-图9所示。

应用本发明控制方法后：

转子角度跟踪信号x1和期望信号x1d如图2所示；转子磁链跟踪信号x5和期望信号x5d如图3所示；转子角位置跟踪误差z1如图4所示；转子磁链跟踪误差z5如图5所示。

由图2-图5看出，异步电动机驱动系统的输出很好的跟踪期望信号。

q轴定子电压和d轴定子电压如图6和图7所示。

由图6和图7看出，真实控制律uqs和uds都稳定在一个有界区域内。

异步电动机状态量的约束空间如图8和图9所示。

由图8和图9可以看出，异步电动机的各个状态量都在约束空间内。

以上仿真结果表明，本发明中考虑铁损的基于状态约束的异步电动机命令滤波模糊控制方法可以高效地跟踪参考信号，因此，具有良好实际实施意义。

当然，以上说明仅仅为本发明的较佳实施例，本发明并不限于列举上述实施例，应当说明的是，任何熟悉本领域的技术人员在本说明书的教导下，所做出的所有等同替代、明显变形形式，均落在本说明书的实质范围之内，理应受到本发明的保护。