基于日最小负荷置信区间的光伏发电准入容量确定方法与流程

本发明属于含分布式光伏发电的配电网规划和设计领域，具体涉及一种基于日最小负荷置信区间的光伏发电准入容量确定方法。

背景技术：

随着我国环境问题的凸显，分布式光伏发电作为解决环境问题的有效手段之一，近十年来快速增长。据统计，截止2019年3月底，全国光伏累计并网装机1.8亿千瓦，其中分布式光伏约5340万千瓦，占比提升至29.8％，低压接入分布式光伏的规模也在逐渐增加。与传统配电网潮流单向流动不同，随着分布式光伏发电的接入，若其并网功率不能完全由本地负荷消纳，将会导致配电网潮流逆流，进而可能导致分布式光伏发电并网点电压越限。因此，开展低压系统分布式光伏准入容量研究对配电网规划及运行具有重要意义。

传统上，关于确定分布式光伏发电准入容量的方法，有文献建立了以电压约束、潮流约束以及分布式电源容量约束的优化模型，利用遗传算法对该模型进行求解，得到了配电网中分布式电源的最大准入容量。有文献建立了含负荷不确定性的分布式电源接入配电网最大准入容量的双层数学模型，然后将双层问题转换为多个单层问题进行求解，该方法能较好地求解分布式电源准入容量问题和对分布式电源的薄弱环节进行判断。有文献在优化模型中考虑了影响分布式光伏发电的随机性因素，借助改进的粒子群算法对模型求解，得到了分布式分布式光伏发电的准入容量，该方法能提升分布式光伏发电的准入容量而不使电压越限。这些文献从不同的角度，建立了不同的优化模型，借助不同的求解方法，试图使分布式光伏发电准入容量的确定更加精确。但数学优化模型的建立和求解较为复杂，模型的求解耗时较长。因此，有必要寻求一种满足实际工程需求的简化方法来确定配电网中分布式光伏发电的准入容量。

现有技术中，也有文献提出了含分布式光伏发电配电网的简化分析方法。有文献提出了一种过电压限制下分布式光伏发电峰值容量的简化计算方法，但该方法仅对0.4kv低压配电网进行解析式分析，且未给出无功补偿量确定的解析式。有文献针对典型的配电网负荷分布，提供了经简化的实用计算函数，但该方法只考虑了3种典型的负荷分布，存在一定的局限性。有文献提出了一种将低压系统等效为两节点模型的简化方法，用以分析系统中分布式光伏发电对系统中最大电压的影响，但未给出确定分布式光伏发电准入容量的解析式。有文献分析了光伏电站内部的无功需求和无功特点，提出了利用多种无功补偿器相互配合的补偿方案，但未考虑光伏逆变器的无功补偿能力，因此，可能造成配置的无功容量偏大，不够经济。有文献提出了一种分析配电网低压系统电压抬升的方法，但在求解无功补偿量时，并未考虑光伏逆变器功率因数限制。有文献提出了一种确定低压系统分布式光伏发电准入容量的简化方法，通过时域仿真验证了该方法的有效性，但该方法仅适用于简单的低压居民用户馈线。

总的来说，配电网中分布式光伏发电准入容量与各节点的负荷大小密切相关，但上述文献中，计算的准入容量都是某个特定的值，并未对配电网中历史负荷数据进行分析，得到的准入容量可能偏保守，也有可能偏乐观。

技术实现要素：

本发明的目的在于克服上述缺点，提出通过一个含概率分布特征的置信区间来表达分布式光伏发电的准入容量，提高分布式光伏发电准入容量的计算准确性和科学性的基于日最小负荷置信区间的光伏发电准入容量确定方法。

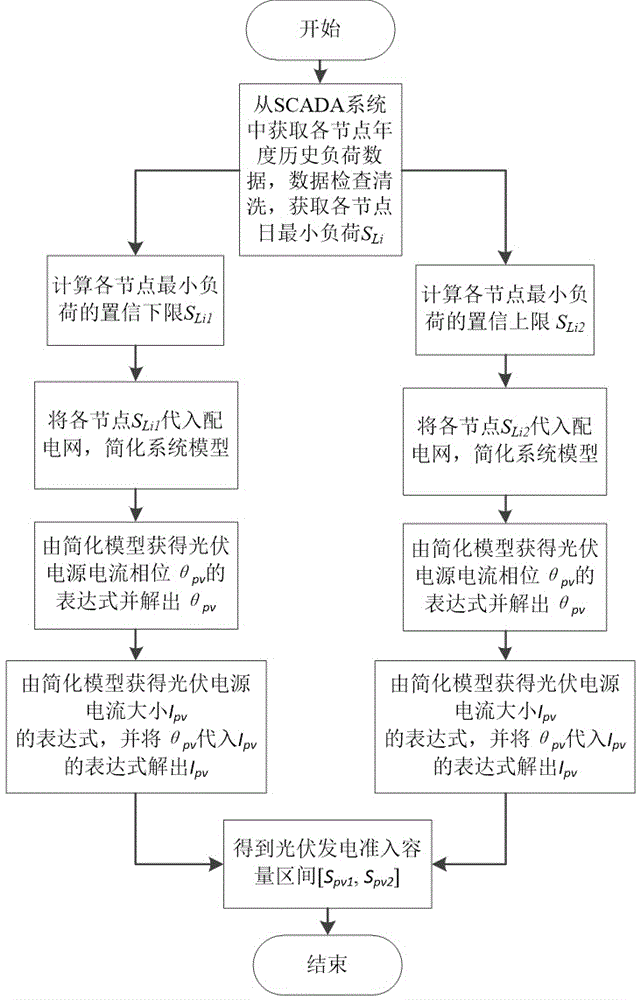
如图1所示，本发明的基于日最小负荷置信区间的分布式光伏发电准入容量确定方法，包括以下步骤：

步骤1：从配电网的数据采集与监视控制(scada)系统中获取各节点年度历史负荷数据，并利用均值插补法和四分位法清洗获取的数据，从清洗出来的数据中提取各节点的日最小负荷sli，其中i表示节点编号。

所述scada系统的采样时间间隔一般为5分钟或15分钟。

所述均值插补法用于对数据缺失值的填补，具体方法为如式(1)所示：

式(1)中lj,d0,t,i等于第i个节点季节j中除了第d0天t时刻外的季节j每天t时刻的负荷的算术平均值，表示第i个节点季节j中第d0天t时刻的填补值，单位一般为kva，其中j＝1、2、3、4分别表示春夏秋冬四个季节，m为季节j包含的天数。

所述四分位法用于来源于scada系统的各节点历史负荷数据异常值处理场景。记第i个节点的年度历史负荷数据按大小顺序排列的矢量为si＝[si,1,si,2,si,3,…,si,n]，其中年负荷采样点数n＝60/15*24*365＝35040，则第二分位数mi(单位一般为kva)为si的中位数，如式(2)所示：

mi＝(si,n/2+si,(n+2)/2)/2(2)

因为n为偶数，所以mi将si分为长度相同的两个子序列，记为si_1＝[si,1,si,2,…,si,n/2]和si_2＝[si,(n+2)/2,si,(n+4)/2,…,si,n]，25％分位点q1,i、75％分位点q3,i分别为子序列si_1和si_2的中位数。由此得到si的四分位间距iqri为q3,i和q1,i之差。所以，在[q1,i-1.5*iqri,q3,i+1.5*iqri]范围内的数据为正常值，而该范围之外的值为异常值。上述数据中异常值同样可通过均值插补法进行替换。

通过上述方法将各节点的年度历史负荷数据进行检查清洗。数据清洗完成后，计算每天各时刻整个系统的总负荷，获取每天所有时刻中总负荷最小值，将总负荷最小值对应时刻的各节点负荷作为各自节点该天的日最小负荷sli。

步骤2：计算各节点的日最小负荷置信下限sli1和置信上限sli2。依据查表法，由z检验表可确定一定置信水平下的zc系数，因此，置信下限为：

置信上限为：

式(3)和(4)中为节点i的日最小负荷均值，sli和n分别为节点i的日最小负荷标准差和样本空间。若取一年的历史负荷数据，则样本空间n为365。

步骤3：将步骤2中计算的日最小负荷置信区间上、下限分别代入所在的辐射型配电系统(如图2所示)，简化该系统的数学模型，求出该简化模型(如图3所示)中发电侧等效阻抗zg,n、线路等效阻抗zc,n、负荷侧等效阻抗zl,n，单位一般为ω。各阻抗可通过式(5)进行n次化简而得。假设各节点电压均为参考电压，一般为1.0p.u.，各节点负荷用恒阻抗模型表示。

式(5)中，k＝1,2,3,…,n；||表示两个阻抗的并联；k＝1时，zg,0、zl,0和zc,0分别为距离外部电网等效电源最近的两个负荷及它们之间的线路阻抗。

步骤4：根据步骤3中的简化模型得到光伏电源电流相角θpv的表达式，并解出θpv，单位一般为度。由于步骤5呈现的式(9)中为光伏逆变器功率因数角，等号左边电流幅值为实数，而右边为复数表达式，表明其虚数部分为0，所以有：

式(6)中只有θpv是未知量，由此可进一步得电流相角θpv为：

步骤5：在分布式光伏发电并网点电压及逆变器功率因数限制下，利用基尔霍夫电流定理，根据步骤3中的简化模型获得光伏电源电流幅值ipv的表达式，并将步骤4中解出的θpv代入ipv的表达式解出ipv，单位一般为ka。所述ipv表达式如式(8)和式(9)所示：

式(8)中，vm为光伏并网点电压上限，单位一般为kv，θpv和θv分别为光伏电源电流相角和并网点电压相角，单位一般为度，θcl和θc分别为阻抗zcl和zc,n的相角，单位一般亦为度。式(8)等号两边除以e^jθpv可进一步得ipv表达的另一种形式，

式(9)中为光伏逆变器功率因数角，单位一般为度。

步骤6：计算分布式光伏发电准入容量的上下限spv2和spv1。将电流相角θpv分别代入式(8)和式(9)可得光伏并网点电压相角θv和光伏电源电流ipv，所以在考虑并网点电压和光伏逆变器功率因数约束下(其中典型的光伏逆变器功率因数曲线如图4所示)，该分布式光伏发电准入容量下限spv1(单位一般为kva)为：

该分布式光伏发电准入容量上限spv2(单位一般为kva)为：

式(10)和(11)中，下标1、2分别表示该变量在日最小负荷置信区间下、上限下对应的值。

本发明与现有技术相比，具有以下优点：

1、相较于传统利用各节点最小负荷经验估计值或某一时段内的最小负荷值计算配电网分布式光伏发电准入容量的方法，本发明引入配电系统历史负荷的概率分布，通过各节点日最小负荷置信区间，求取低压系统电压及光伏逆变器功率因数的约束下分布式光伏发电准入容量的上限和下限，实现了分布式光伏发电准入容量确定的置信区间表达，提高了计算的准确性、科学性，对相关工程更具科学指导意义。

2、相较于传统利用详细配电网模型计算配电网分布式光伏发电准入容量的方法，本发明从配电网模型简化角度出发，构建数学模型，省去了较为复杂的迭代分析，提高了计算的易用性，对相关工程更具实用意义。

附图说明

图1是本发明的流程图；

图2是本发明的一个含分布式光伏发电的配电网详细模型；

图3是本发明的一个简化后含分布式光伏发电的配电网模型；

图4是本发明的一个光伏逆变器功率因数曲线示意图；

图5是实施例中一个ieee69节点配电系统模型示意图；

图6是实施例中一个通过本发明方法简化后的ieee69节点系统模型；

图7是实施例中涉及的11种负荷分布的90％置信水平下日最小负荷置信区间。

具体实施方式

以下结合附图和实施例详细描述本发明的具体实施方式，但本发明不受所述具体实施例所限。

依据本发明步骤：

如图1所示，本发明的基于日最小负荷置信区间的分布式光伏发电准入容量确定方法，包括以下步骤：

步骤1：从配电网的数据采集与监视控制(scada)系统中获取各节点年度历史负荷数据，并利用均值插补法和四分位法清洗获取的数据，从清洗出来的数据中提取各节点的日最小负荷sli，其中i表示节点编号。

所述scada系统的采样时间间隔一般为5分钟或15分钟。

所述均值插补法用于对数据缺失值的填补，具体方法为如式(1)所示：

式(1)中lj,d0,t,i等于第i个节点季节j中除了第d0天t时刻外的季节j每天t时刻的负荷的算术平均值，表示第i个节点季节j中第d0天t时刻的填补值，单位一般为kva，其中j＝1、2、3、4分别表示春夏秋冬四个季节，m为季节j包含的天数。

所述四分位法用于来源于scada系统的各节点历史负荷数据异常值处理场景。记第i个节点的年度历史负荷数据按大小顺序排列的矢量为si＝[si,1,si,2,si,3,…,si,n]，其中年负荷采样点数n＝60/15*24*365＝35040，则第二分位数mi(单位一般为kva)为si的中位数，如式(2)所示：

mi＝(si,n/2+si,(n+2)/2)/2(2)

因为n为偶数，所以mi将si分为长度相同的两个子序列，记为si_1＝[si,1,si,2,…,si,n/2]和si_2＝[si,(n+2)/2,si,(n+4)/2,…,si,n]，25％分位点q1,i、75％分位点q3,i分别为子序列si_1和si_2的中位数。由此得到si的四分位间距iqri为q3,i和q1,i之差。所以，在[q1,i-1.5*iqri,q3,i+1.5*iqri]范围内的数据为正常值，而该范围之外的值为异常值。上述数据中异常值同样可通过均值插补法进行替换。

通过上述方法将各节点的年度历史负荷数据进行检查清洗。数据清洗完成后，计算每天各时刻整个系统的总负荷，获取每天所有时刻中总负荷最小值，将总负荷最小值对应时刻的各节点负荷作为各自节点该天的日最小负荷sli。

步骤2：计算各节点的日最小负荷置信下限sli1和置信上限sli2。依据查表法，由z检验表可确定一定置信水平下的zc系数，因此，置信下限为：

置信上限为：

式(3)和(4)中为节点i的日最小负荷均值，sli和n分别为节点i的日最小负荷标准差和样本空间。若取一年的历史负荷数据，则样本空间n为365。

步骤3：将步骤2中计算的日最小负荷置信区间上、下限分别代入所在的辐射型配电系统(如图2所示)，简化该系统的数学模型，求出该简化模型(如图3所示)中发电侧等效阻抗zg,n、线路等效阻抗zc,n、负荷侧等效阻抗zl,n，单位一般为ω。各阻抗可通过式(5)进行n次化简而得。假设各节点电压均为参考电压，一般为1.0p.u.，各节点负荷用恒阻抗模型表示。

式(5)中，k＝1,2,3,…,n；||表示两个阻抗的并联；k＝1时，zg,0、zl,0和zc,0分别为距离外部电网等效电源最近的两个负荷及它们之间的线路阻抗。

步骤4：根据步骤3中的简化模型得到光伏电源电流相角θpv的表达式，并解出θpv，单位一般为度。由于步骤5呈现的式(9)中为光伏逆变器功率因数角，等号左边电流幅值为实数，而右边为复数表达式，表明其虚数部分为0，所以有：

式(6)中只有θpv是未知量，由此可进一步得电流相角θpv为：

步骤5：在分布式光伏发电并网点电压及逆变器功率因数限制下，利用基尔霍夫电流定理，根据步骤3中的简化模型获得光伏电源电流幅值ipv的表达式，并将步骤4中解出的θpv代入ipv的表达式解出ipv，单位一般为ka。所述ipv表达式如式(8)和式(9)所示：

式(8)中，vm为光伏并网点电压上限，单位一般为kv，θpv和θv分别为光伏电源电流相角和并网点电压相角，单位一般为度，θcl和θc分别为阻抗zcl和zc,n的相角，单位一般亦为度。式(8)等号两边除以e^jθpv可进一步得ipv表达的另一种形式，

式(9)中为光伏逆变器功率因数角，单位一般为度。

步骤6：计算分布式光伏发电准入容量的上下限spv2和spv1。将电流相角θpv分别代入式(8)和式(9)可得光伏并网点电压相角θv和光伏电源电流ipv，所以在考虑并网点电压和光伏逆变器功率因数约束下(其中典型的光伏逆变器功率因数曲线如图4所示)，该分布式光伏发电准入容量下限spv1(单位一般为kva)为：

该分布式光伏发电准入容量上限spv2(单位一般为kva)为：

式(10)和(11)中，下标1、2分别表示该变量在日最小负荷置信区间下、上限下对应的值。

实施例：

为验证本发明方法的有效性，用ieee69节点辐射型配电系统(如图5所示)进行实施例分析，选取系统中节点1,2,…,26,27作为主干线，将其余分支线视为负荷，分别接在主干线上，分布式光伏发电经升压变t1接入末端节点17上，如图6所示。其中n为27，额定电压为12.66kv，系统总负荷为3802.19+j2694.6kva。配电线路n0-n1阻抗为0.27+j0.12ω/km，长度为0.05km，升压变t1额定容量为5mva，其阻抗标幺值为0.0199+j0.0458。zl1和zl28设为0负荷，即zl1和zl28阻抗无穷大。设节点0电压为1.04p.u.，1.07p.u.为并网点电压上限，取光伏逆变器功率因数在±0.98范围内连续可调。

实施例测试：本发明分布式光伏发电准入容量计算方法的有效性测试

a)年度历史负荷建模

实施例利用digsilent软件模拟scada系统中各节点年度历史负荷数据，digsilent中内置11种不同的年负荷分布，每种负荷曲线的建立相同，分为4个季节，其中每个季节又分为工作日和非工作日，如表1所示。

表1年负荷的建模方法

表1为年负荷分布的建模方法，含winter(冬)，uebergang_1(春)，sommer(夏)和uebergang_2(秋)四个季节，每个季节由工作日和非工作日组成，非工作日又分为周六和周日，因此每个季节的负荷均由三个日负荷分布构成，如winter季节中周一到周五的日负荷分布均为winter_werktag(工作日-冬)，周六的日负荷分布为winter_samtag(周六-冬)，周日的日负荷分布为winter_sonntag(周日-冬)。四个不同季节的定义如表2所示。

表2季节的定义

从表2可以看出，digsilent软件中将每年3月21日-5月14日定义为春季，5月15日-9月14日定义为夏季，9月15日-10月31日定义为秋季，11月1日-次年3月20日定义为冬季。根据上述年负荷建模方法，对数据进行检查清洗后得到11种采样时间间隔为15分钟的年负荷分布曲线。

b)分布式光伏发电准入容量计算方法有限性验证

本发明方法在matlab软件中编程实现，然后利用德国digsilent软件搭建ieee69节点系统进行仿真验证。根据负荷的地理分布，将系统中48个负荷分为11个区域，如表3所示，每个区域中巅峰负荷不同但负荷分布相同，各种分布下日最下负荷置信区间如图7所示，横坐标为负荷分布类型名称，纵坐标为负荷大小，单位：p.u.。

依据查表法，由z检验表可确定某置信水平下的置信系数，如置信水平为0.9时，zc＝1.64，置信水平为0.95时，zc＝1.96，置信水平为0.99时，zc＝2.58。实施例中取置信水平为0.9，其他置信水平下计算方法相同。在分布式光伏发电逆变器在单位功率因数及超前功率因数两种工况下，本发明方法及digsilent仿真所得结果分别记录于表4和表5中。

表3负荷分区

表4电压限制及单位功率因数下分布式光伏发电准入容量计算结果

表4中，v0、vlm、delta、ppv、qpv、pg和qg分别为系统首端电压、光伏并网点电压及相角、光伏和电网侧有功无功出力，下同。由表4看出，光伏逆变器工作于单位功率因数方式下，分布式光伏发电准入容量为[290.99kw，289.99kw]，不能完全满足系统负荷需求，额外的需求通外部电网供给，分布式光伏发电有功出力误差为0.83％，为所有误差中最小值，电网侧有功出力误差7.12％为各项误差中最大值。

表5电压及功率因素限制下分布式光伏发电准入容量计算结果

在光伏逆变器功率因数限制和电压约束下，本发明方法与digsilent时域仿真对比结果如表5所示。其中，利用日最小负荷置信下限得到的光伏有功出力为321.88kw，比表4工况下多了约32kw，分布式光伏发电的利用效率提升了11.1％，无功吸收量为65.36kvar。光伏逆变器无功吸收量误差7.44％为各项误差中最大值。

由表4和表5可以看出，分布式光伏发电准入容量区间长度较小，不足准入容量下限的1％，在实际工程中，可取分布式光伏发电准入容量区间的上、下限的均值作为参考。本发明方法结果与digsilent软件仿真结果接近，存在一定误差，各项误差均小于8％，最大值为表5中光伏逆变器无功吸收量误差[7.44％,7.46％]，产生误差的原因是本发明中假设了系统各节点电压不变，且等于首节点电压。但实际上，各节点电压是不相等的，又由于本发明取的是系统日最小负荷，各节点间电压误差较小，基本与假设相符。本发明中所提方法与专业电力系统分析软件digsilent之间的误差在8％以内，满足实际工程需要，由此验证了本发明方法的有效性。