一种改进的感应电机模型预测直接转矩控制方法与流程

本发明涉及异步电机的模型预测控制领域，特别是一种改进的感应电机模型预测直接转矩控制方法。

背景技术：

近三十年来，模型预测控制(mpc)是过程控制领域中取得的最重要的进展之一。在车辆牵引和悬挂控制、汽车动力系统和热管理等领域得到了广泛应用。随着一些控制平台如digitalsignalprocessors(dsp)和fieldprogrammablegatearrays(fpga)的不断更新换代，使得电力电子硬件设备的计算能力经历了持续的增长这种强大的计算能力使得实现新的、通常更复杂的控制技术成为可能，例如模糊控制、自适应控制、滑模控制和预测控制，在电气传动领域，最广为人知的控制策略是磁场定向控制(foc)和直接转矩控制(dtc)，它们是工业应用中电机驱动的标准闭环控制方案。它们对电网系统的双重实现是电压定向控制和直接功率控制(dpc)。mpc作为近年来新兴的控制方法，可以比dtc更为精确和高效的选择电压矢量，并且在稳态下拥有更小的转矩脉动。虽然mpc的电流总谐波畸变率(totalharmonicdistortion，thd)高于foc的thd，但在动态性能上要优于foc。因此，mpc在电气传动领域的应用有着很大的发展潜力。

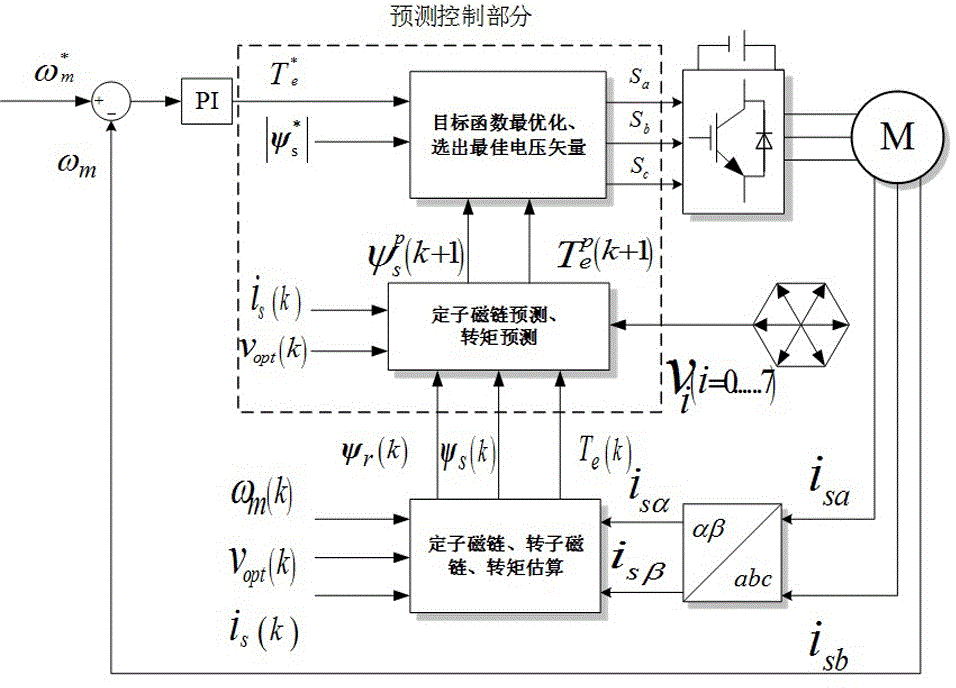
如图1所示，传统异步电机模型预测直接转矩控制中存在的转矩脉动和计算量大等问题。

技术实现要素：

本发明的目的在于提供一种改进的感应电机模型预测直接转矩控制方法，以克服传统异步电机模型预测直接转矩控制中存在的转矩脉动和计算量大等问题。

为实现上述目的，本发明的技术方案是：一种改进的感应电机模型预测直接转矩控制方法，按照如下步骤实现：

步骤s1、测量：在tk时刻采样获得定子电流is(k)；

步骤s2、估算：分别用式(1)、(2)估算tk时刻的转子磁通和定子磁通；

式中，为tk时刻的转子磁通；为tk-1时刻的转子磁通；为tk时刻的定子磁通；ts为采样周期；rr为转子电阻；ls、lr和lm分别为定子电感、转子电感和定转子互感；kr为转子耦合系数；ω(k)为tk时刻的转子角速度，j是虚数标记；

步骤s3、延时补偿：启动过电流保护，把上一循环获得的最优电压矢量vbest(k-1)代入到式(3)、(4)、(5)分别得到tk+1时刻的定子磁链、定子电流和电磁转矩；

式中，ψsp(k+1)为tk+1时刻的定子磁链；isp(k+1)为tk+1时刻的定子电流；为tk+1时刻的定子磁链的共轭；tp(k+1)为tk+1时刻的电磁转矩；rs为定子电阻；τσ＝σls/rσ；im{}为{}内复数的虚部；p为极对数；vs(k)为tk时刻的定子电压矢量；τr为转子时间常数；ω(k)为tk时刻的转子角速度；

步骤s4、筛选电压矢量：根据相邻电压矢量原理结合扇区划分表、电压矢量选择表从8个电压矢量中筛选出3个电压矢量；

步骤s5、转矩变化量计算：在tk+1时刻计算转矩变化量δti(k)；

δti(k)＝tp,i(k+1)-tp,i(k)(6)

式中tp,i(k+1)为tk+1时刻的电压矢量vi对应的电磁转矩；δti(k)为电压矢量vi对应的转矩变化量；

步骤s6、简化两步预测：用式(7)预测tk+2时刻的定子磁链，再将获得的tk+1时刻的电压矢量vi对应的电磁转矩和电压矢量vi对应的转矩变化量δti(k)相加获得tk+2时刻的电压矢量vi对应的电磁转矩；

ψsp(k+2)＝ψsp(k+1)+tsvs(k+1)-rstsis(k+1)(7)

tp,i(k+2)＝tp,i(k+1)+δti(k)(8)

其中，tp,i(k+2)为tk+2时刻的电压矢量vi对应的电磁转矩；

步骤s7、选择最优电压矢量：把步骤s6获得的目标量预测值代入到式(9)，将筛选后的3个电压矢量分别对应的代价函数值进行排序，把最小值对应的电压矢量作为最优电压矢量；

式中λ为权重系数，该值被用于调节转矩与定子磁链控制所占的比重；gi,j为代价函数，i为对应电压矢量编号；t^*为电机转矩额定值；ψsp,i(k+2)为tk+2时刻的电压矢量vi对应的定子磁链；tp,j(k+3)为tk+3时刻的电压矢量vi对应的电磁转矩；ψsp,j(k+3)为tk+3时刻的电压矢量vi对应的定子磁链；|ψ^*s|为电机定子磁链额定幅值；

步骤s8、将最优电压矢量应用在下一个采样周期，返回步骤s1。

在本发明一实施例中，所述步骤s4具体实现如下：

将磁链空间划分为6个扇区，其中，θ是定子磁链位置，n＝1，2，…，6，ψsβ、ψsα分别是定子磁链在β轴、α轴上的磁链数值，可估算如下：

θ＝arctan(ψsβ/ψsα)

(2n-3)π/6≤θ(n)≤(2n-1)π/6

由此构建扇区划分表；

而后依据：当δte>0时，所选择的电压矢量必须能增加预测电磁转矩，可沿逆时针方向移动定子磁链轨迹并增加电磁转矩的矢量；当δte<0时，所选择的电压矢量必须能减小预测电磁转矩，可沿顺时针方向移动定子磁链速度轨迹并减小电磁转矩的矢量；当δte＝0时，使用零电压矢量来阻止定子磁通的位移；其中，δte＝te-te^p，te为电磁转矩参考值；te^p电磁转矩预测值；δte为电磁转矩参考值与预测值之差；

由此构建电压矢量选择表；

基于扇区划分表、电压矢量选择表，根据定子磁链位置所处扇区，即可从8个电压矢量中筛选出3个电压矢量。

相较于现有技术，本发明具有以下有益效果：本发明提供了一种改进的感应电机模型预测直接转矩控制方法，该方法结合开关表从8个电压矢量中筛选出3个电压矢量，之后在延时补偿的基础上进行两步磁链预测和一步转矩预测，并分别计算3个电压矢量在第一步转矩预测中对应的转矩变化量，根据转矩变化量完成第二步的转矩预测，最后选出能使代价函数最小的电压矢量作用于逆变器。通过开关表筛选出待预测的电压矢量，缩小了开关状态的选择范围，降低了算法的复杂度，在传统的mptc两步预测中需要进行72＝49次的计算，而本方法只需要计算32＝9次。并且本文还简化了第二步的转矩预测计算，总体上极大地降低了数字控制系统的计算时间，提高了系统采样频率，所以整个系统的控制性能进一步提升了。最后，通过实验验证分析了所提出的改进的mptc在感应电机控制上的可行性、有效性。

附图说明

图1为传统的异步电机直接转矩预测控制框图；

图2为相邻电压矢量选择原理图；

图3为两步预测与单步预测转矩脉动比较；

图4为新型模型预测直接转矩控制流程图。

具体实施方式

下面结合附图，对本发明的技术方案进行具体说明。

本发明提供了一种改进的感应电机模型预测直接转矩控制方法，按照如下步骤实现：

步骤s1、测量：在tk时刻采样获得定子电流is(k)；

步骤s2、估算：分别用式(1)、(2)估算tk时刻的转子磁通和定子磁通；

式中，为tk时刻的转子磁通；为tk-1时刻的转子磁通；为tk时刻的定子磁通；ts为采样周期；rr为转子电阻；ls、lr和lm分别为定子电感、转子电感和定转子互感；kr为转子耦合系数；ω(k)为tk时刻的转子角速度，j是虚数标记；

步骤s3、延时补偿：启动过电流保护，把上一循环获得的最优电压矢量vbest(k-1)代入到式(3)、(4)、(5)分别得到tk+1时刻的定子磁链、定子电流和电磁转矩；

式中，ψsp(k+1)为tk+1时刻的定子磁链；isp(k+1)为tk+1时刻的定子电流；为tk+1时刻的定子磁链的共轭；tp(k+1)为tk+1时刻的电磁转矩；rs为定子电阻；τσ＝σls/rσ；im{}为{}内复数的虚部；p为极对数；vs(k)为tk时刻的定子电压矢量；τr为转子时间常数；ω(k)为tk时刻的转子角速度；

步骤s4、筛选电压矢量：根据相邻电压矢量原理结合扇区划分表、电压矢量选择表从8个电压矢量中筛选出3个电压矢量；

步骤s5、转矩变化量计算：在tk+1时刻计算转矩变化量δti(k)；

δti(k)＝tp,i(k+1)-tp,i(k)(6)

式中tp,i(k+1)为tk+1时刻的电压矢量vi对应的电磁转矩；δti(k)为电压矢量vi对应的转矩变化量；

步骤s6、简化两步预测：用式(7)预测tk+2时刻的定子磁链，再将获得的tk+1时刻的电压矢量vi对应的电磁转矩和电压矢量vi对应的转矩变化量δti(k)相加获得tk+2时刻的电压矢量vi对应的电磁转矩；

ψsp(k+2)＝ψsp(k+1)+tsvs(k+1)-rstsis(k+1)(7)

tp,i(k+2)＝tp,i(k+1)+δti(k)(8)

其中，tp,i(k+2)为tk+2时刻的电压矢量vi对应的电磁转矩；

步骤s7、选择最优电压矢量：把步骤s6获得的目标量预测值代入到式(9)，将筛选后的3个电压矢量分别对应的代价函数值进行排序，把最小值对应的电压矢量作为最优电压矢量；

式中λ为权重系数，该值被用于调节转矩与定子磁链控制所占的比重；gi,j为代价函数，i为对应电压矢量编号；t^*为电机转矩额定值；ψsp,i(k+2)为tk+2时刻的电压矢量vi对应的定子磁链；tp,j(k+3)为tk+3时刻的电压矢量vi对应的电磁转矩；ψsp,j(k+3)为tk+3时刻的电压矢量vi对应的定子磁链；|ψ^*s|为电机定子磁链额定幅值；

步骤s8、将最优电压矢量应用在下一个采样周期，返回步骤s1。

本实例中，在所述步骤s1中，在定子参考坐标系下，三相感应电机的数学模型可由式(10)至式(14)表示

ψs＝lsis+lmir(12)

ψr＝lrir+lmis(13)

在上述感应电机数学模型5个式子中，vs为定子电压矢量；ψs和ψr分别为定子与转子磁链矢量；is和ir分别为定子与转子电流矢量；rs和rr分别为定子电阻和转子电阻；ls、lr和lm分别为定子电感、转子电感和定转子互感；ωr为转子角速度；te和p分别为电磁转矩和极对数。

在转子参考坐标系下，定子磁通、转子磁通和定子电流间关系可表示为

通过欧拉公式将式(15)离散化得到转子磁链估计的离散方程为公式(1)，最后将式(1)代入式(16)获得定子磁链估计的离散方程为(2)，式中ts为采样周期；ks＝lm/lr。

同理，通过欧拉公式和感应电机数学模型可以推导出定子磁链预测值和定子电流预测值式子(3)和(4)，式中τσ＝σls/rσ；rσ＝rs+kr²rr；σ＝1-(l²m/lslr)。

将式(3)和(4)代入式(14)可求得电磁转矩的预测值为式子(5)。

本实例中，在所述步骤3中，在控制系统中采用适当的延时补偿可以减小延时对控制性能的影响。在tk时刻应用上一时刻计算获得的电压矢量v(k-1)与此刻测量获得的x(k)来预测tk+1时刻的x(k+1)，之后根据x(k+1)再进行一步预测获得x(k+2)，选择最佳电压矢量应用在tk+1时刻。

在所述步骤4中，仅仅用电磁转矩偏差δte＝te-tep和磁链角度θ所在扇区位置就可以预测由预测直接转矩控制(pdtc)使用的电压矢量。为了快速判断磁链所在位置并筛选电压矢量，我们可以将磁链空间划分为6个扇区，扇区划分如下表1所示，其中θ是定子磁链位置n＝1，2，…，6，ψsβ、ψsα分别是定子磁链在β轴、α轴上的磁链数值，可估算如下：

θ＝arctan(ψsβ/ψsα)

(2n-3)π/6≤θ(n)≤(2n-1)π/6

假设定子磁链位置用位于第2扇区t1时刻的角度θsr表示，当δte>0时，所选择的电压矢量必须能增加预测电磁转矩，可沿逆时针方向移动定子磁链轨迹并增加电磁转矩的矢量为和如图2所示。逆变器提供的相应电压矢量为υ3和υ4。同样，当δte<0时，所选择的电压矢量必须能减小预测电磁转矩，可沿顺时针方向移动定子磁链速度轨迹并减小转矩的是分别与υ3和υ4相反的电压矢量，即υ6和υ1。当δte＝0时，使用零电压矢量来阻止定子磁通的位移，有助于将转矩脉动和磁链脉动保持在一定范围内。因此，对于两电平电压源型逆变器，表2中总结了同时满足转矩偏差和磁链位置的所有相邻的电压矢量情况。

表1扇区的划分

表2电压矢量选择表

本实例中，在所述步骤5和步骤6中，多步模型预测控制是在一个周期中预测tk+1和tk+2两个时刻的被控量，δt1'和δt2'分别为两个时刻的电磁转矩值。将tk+2时刻的被控量预测值代入到目标函数中选取最优电压矢量作用于tk时刻。

如图3所示，因为采样周期ts远远小于电机定子电流周期t1，可以假设在单个采样周期内转矩是线性变化的，则每一个电压矢量在一个采样周期内对应一条转矩变化轨迹，因此可以假设当前采样周期内每一个电压矢量所产生的转矩变化量等于下一个采样周期内相应矢量的转矩变化量，即δti(k)＝δti(k+1)。

根据上述理论，可将转矩的第二步预测做如下简化。首先在tk时刻根据公式计算出

电磁转矩，再通过预测模型获得各电压矢量对应的转矩预测值，然后计算出各电压矢量的转矩变化量，最后将第一步的转矩预测值和转矩变化量相加获得第二步预测值。计算过程可由下式表示

δti(k)＝tp,i(k+1)-tp,i(k)

tp,i(k+2)＝tp,i(k+1)+δti(k)

式中tp,i(k+1)为第一步预测的tk+1时刻的电压矢量vi对应的电磁转矩；δti(k)为第二步预测的电压矢量vi对应的转矩变化量；定子磁链预测值可由式(3)推导获得

ψsp(k+2)＝ψsp(k+1)+tsvs(k+1)-rstsis(k+1)

综上所述，针对本发明中所提出的改进型mptc，做出其控制算法流程图。如图4所示。

以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。