一种基于模型预测控制的无线传能动态性能优化方法与流程

本发明属于无线电能传输技术领域，具体涉及一种基于模型预测控制的无线传能动态性能优化方法。

背景技术：

感应式无线传能技术(ipt)作为一种灵活可靠的非接触式电源方式，可以有效地避免了插电系统存在的电火花、漏电等安全问题。随着电力电子技术、补偿网络设计和耦合器设计的发展，感应式无线传能系统在恶劣环境下的高效率和可靠性已经得到了证明。在过去的十年里，这项技术被广泛应用于许多应用领域，如智能手机、电动汽车和电动巴士。

通常一个ipt系统包含高频转换器、磁耦合器、高阶补偿网络和其他非线性元件。复杂的系统结构和高工作频率使感应式无线传能系统的有效控制变得很困难，特别是在瞬态系统中这个问题尤为突出。如在动态感应式无线传能系统中，耦合系数和等效负载电阻在接收线圈的车辆移动时各不相同。即使在一些静态感应式无线传能系统中，系统输入电压的波动和脉冲的功率负载也是不可避免的。这些问题可能导致系统效率的急剧下降和连续的功率振荡。

现有文献中关于输入电压和负载宽范围内实现较高功率转移和效率优化的方法，可采用基于负载匹配的最大效率跟踪方法(meet)，通过调节系统的变流器以优化线圈中的电流，从而可以减小线圈中的功率损失。但是在计算最优效率点时，总是将ipt系统的组成部分理想化。忽略开关和无源器件的寄生电阻，会导致最优效率跟踪不精确。此外，目前的动态ipt系统控制方案在系统输入电压或负载参数发生变化时的动态性能较差，导致系统瞬态稳定时间延长和超调/欠调等现象。在ipt系统中，较差的控制器性能将会导致频繁的功率振荡，进而大大降低车载电机、电池等设备的整体效率和寿命，对整个系统的体积和可靠性也提出了额外的要求。

技术实现要素：

本发明的目的在于：

为解决现有技术中的无线电能传输系统中的超调和功率振荡现象导致系统动态性能效率低的问题，提供一种基于模型预测控制的无线传能动态性能优化方法，通过一个简单而精确的离散数学模型，结合对目标函数的滚动优化，对整流器当前时刻的最优移相角进行实时计算，大大改善了ipt系统的动态性能，有效缩短了系统输出电压的响应时间，避免了绝大多数超调和功率振荡现象。

本发明采用的技术方案如下：

一种基于模型预测控制的无线传能动态性能优化方法，包括如下步骤：

a.建立基于有源整流器的s-s补偿ipt系统的动态数学模型；

b.建立基于滚动优化设计和模型预测的动态mpc方案；

c.设计基于恒压输出的效率优化控制方案。

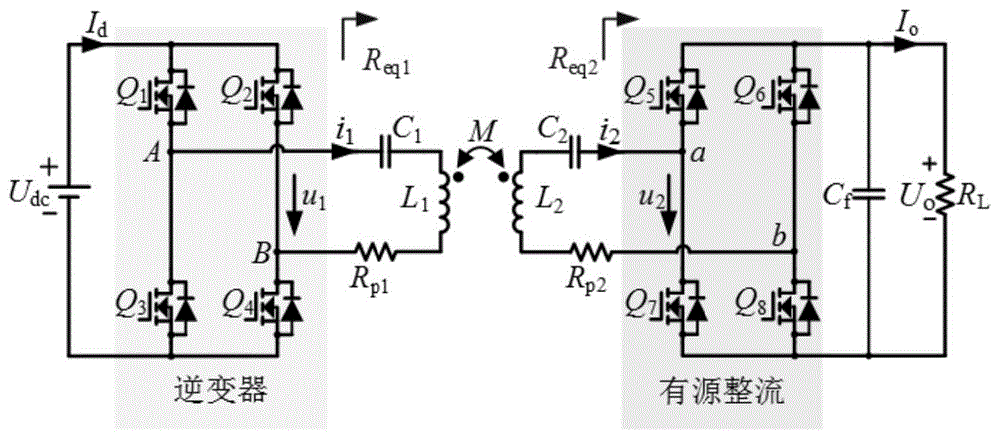
进一步地，基于有源整流器的s-s补偿ipt系统由接收端、发送端两部分组成，其中发送端包括依次与直流电源udc连接的逆变器、逆变器的开关信号q1～q4、发送端补偿电容c1和发送端线圈自感l1，发射线圈和接收线圈之间互感为m；接收端包括依次串接的接收端线圈自感l2、接收端补偿电容c2、有源整流桥及其开关信号q5～q8、整流滤波电容cf和直流负载rl；

设定系统的工作频率为fs，角频率为ωs，基于移相控制，逆变器交流侧等效阻抗为req1，整流器交流侧等效阻抗req2：

其中α是逆变器移相角，β是整流器移相角，u1是逆变器输出电压u1的有效值，i1是逆变器输出电流i1有效值，u2是整流器输入电压u2的有效值，i2是整流器输入电流i2的有效值；

根据ss拓扑ipt系统的基波模型等效电路，建立其基尔霍夫电压方程组：

基于有源整流器的系统输出电压控制建立ipt系统的动态模型，当β＝0°，直流滤波电容的电流可以表示为：

其中，uo是系统输出电压，io是系统输出电流，整流器输入电流为：

将(5)式代入到(4)式：

将式(6)进行平均化和离散化处理分别得到式(7)、式(8)：

其中，tp是整流器的控制周期，k是采样时刻，根据式(8)，系统输出电压增量的动态模型可表示为：

当β≠0时，通过迭代法可以得出k+1时刻的系统输出电压预测值与整流器移相角之间的关系：

进一步地，mpc方案是基于预测模型和可能的控制集来预测系统未来的应用，在滚动优化中确定最优控制操作，使控制目标与参考目标偏差最小；在所提出的控制系统中，mpc方案用于控制整流器的移相角β，从而使输出电压uo逼近参考电压uset，基于预测模型f的系统输出电压为：

其中，m(i)为系统的控制变量，i为当前滚动优化的次数，其与移相控制角的关系为cos(βⁱ(k+1))＝cos(β(k))+m(i)，根据(10)式，可以得到非线性预测模型：

则滚动优化的目标函数为：

minj(m(i),uo(k))

其中，a1和a2为权重系数。

进一步地，所述滚动优化设计包括如下步骤：

步骤①：检测ktp时刻整流器输入电流的有效值i2(k)、整流器输出电压uo(k)和电流io(k)；

步骤②：初始化控制变量m(i)(i＝1)，根据式(12)计算预测输出电压uoⁱ(k+1)，再通过式(13)计算成本函数j(i)；

步骤③：判断滚动优化次数i是否达到预定次数n，若达到，用冒泡排序法求出j(i)的最小值jmin(i)，若未到，则i＝i+1，返回步骤②；

步骤④：由成本函数最小值jmin(i)，找出最优的控制变量和在k时刻整流器移相角β；

使用所述的基于恒压输出的效率优化控制方案：基于mpc调节整流器输入端等效负载后，从控制逆变器的角度入手优化系统效率；

基于有源整流器的s-s补偿ipt系统中，若忽略开关损耗，系统效率表示为：

其中，pin是系统输入功率，pout是系统输出功率，ploss是线圈损耗，rp1是发射线圈寄生电阻，rp2是接收线圈寄生电阻，在恒定输出功率和输出电压的情况下，发射线圈电流i1和接收线圈电流i2：

忽略线圈损耗，发射线圈电流和接收线圈电流可以简化为：

根据式(14)，计算最高效率情况下发射线圈电流和接收线圈电流之间的关系：

将式(17)、(18)代入(19)，解出最大传输效率时，逆变器移相角α与整流器移相角β之间的关系：

进一步地，所述效率优化控制方案包括如下步骤：

步骤1)：检测初始时刻逆变器输入电流id(0)，初始化逆变器移相角α(0)和逆变器移相角增量δα；

步骤2)：在下个采样时刻，将上一时刻的逆变器移相角与移相角增量相加，得到当前逆变器移相角α(1)＝α(0)+δα，并测量此刻的逆变器输入电流id(1)；

步骤3)：根据id(0)和id(1)的大小关系决定扰动观察的方向，若id(1)<id(0)，用α(k+1)＝α(k)+δα来增加α以靠近最佳的逆变器移相角，反之则用α(k+1)＝α(k)-δα来减小α，其中k表示采样时间ktr，tr是逆变器的相位角控制的控制周期；

步骤4)：对于观察扰动的两个方向，将采样时间k+1处的副边电流i2(k+1)与前一个采样时间k处的副边电流i2(k)进行比较，同时比较采样时间k+1处输出电压uo(k+1)与参考电压的差值是否小于参考误差rlim；如果i2(k+1)<i2(k)且|uo(k)-uset|<rlim，则α(k+1)＝α(k)+δα或α(k+1)＝α(k)-δα应持续进行以使α逼近最优的移相角；若i2(k+1)>i2(k)或|uo(k)-uset|>rlim，则意味着α的变化不能进一步降低副边电流，α(k)可以被认为是最优的移相角，相应的是i2(k)是最小副边电流i2min。

综上所述，由于采用了上述技术方案，本发明的有益效果是：

1.本发明通过一种基于有源整流建模的串并联补偿ipt系统的动态数学模型，给ipt系统的控制器提供可靠、简单的计算依据。无需复杂的计算，可以动态预测系统下一采样时刻的输出电压，在保证精度的同时，大大地简化了变流器最优控制方案的计算过程。

2.本发明通过基于滚动计算设计和动态数学模型的动态mpc方案，使ipt系统具有良好的动态性能，建立了mpc方案的成本函数，缩短了求解时间，减少了连续两个控制周期的控制变量的差异，使暂态过程将大大缩短，避免了明显的超调和功率振荡现象。

3.本发明为了实现最大效率跟踪(meet),使用p&o方法来调节逆变器的相角,以最小化系统的输入功率。同时，通过mpc方案控制整流器的相角,获得恒定电压(cv)输出，实现恒压输出ipt系统的效率优化。

附图说明

图1是本发明ss补偿拓扑ipt系统电路图；

图2是本发明的ss补偿拓扑的基波等效电路；

图3是本发明步骤b的流程图；

图4是本发明步骤c的流程图；

图5是本发明控制方案示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

实施例1

一种基于模型预测控制的无线传能动态性能优化方法，包括如下步骤：

a.建立基于有源整流器的s-s补偿ipt系统的动态数学模型；

b.建立基于滚动优化设计和模型预测的动态mpc方案；

c.设计基于恒压输出的效率优化控制方案。

实施例2

在实施例一的基础上，基于有源整流器的s-s补偿ipt系统由接收端、发送端两部分组成，其中发送端包括依次与直流电源udc连接的逆变器、逆变器的开关信号q1～q4、发送端补偿电容c1和发送端线圈自感l1，发射线圈和接收线圈之间互感为m；接收端包括依次串接的接收端线圈自感l2、接收端补偿电容c2、有源整流桥及其开关信号q5～q8、整流滤波电容cf和直流负载rl；

设定系统的工作频率为fs，角频率为ωs，基于移相控制，逆变器交流侧等效阻抗为req1，整流器交流侧等效阻抗req2：

其中α是逆变器移相角，β是整流器移相角，u1是逆变器输出电压u1的有效值，i1是逆变器输出电流i1有效值，u2是整流器输入电压u2的有效值，i2是整流器输入电流i2的有效值；

根据ss拓扑ipt系统的基波模型等效电路，建立其基尔霍夫电压方程组：

基于有源整流器的系统输出电压控制建立ipt系统的动态模型，当β＝0°，直流滤波电容的电流可以表示为：

其中，uo是系统输出电压，io是系统输出电流，整流器输入电流为：

将(5)式代入到(4)式：

将式(6)进行平均化和离散化处理分别得到式(7)、式(8)：

其中，tp是整流器的控制周期，k是采样时刻，根据式(8)，系统输出电压增量的动态模型可表示为：

当β≠0时，通过迭代法可以得出k+1时刻的系统输出电压预测值与整流器移相角之间的关系：

实施例3

在实施例一的基础上，mpc方案是基于预测模型和可能的控制集来预测系统未来的应用，在滚动优化中确定最优控制操作，使控制目标与参考目标偏差最小；在所提出的控制系统中，mpc方案用于控制整流器的移相角β，从而使输出电压uo逼近参考电压uset，基于预测模型f的系统输出电压为：

其中，m(i)为系统的控制变量，i为当前滚动优化的次数，其与移相控制角的关系为cos(βⁱ(k+1))＝cos(β(k))+m(i)，根据(10)式，可以得到非线性预测模型：

则滚动优化的目标函数为：

minj(m(i),uo(k))

其中，a1和a2为权重系数。

实施例4

在实施例一的基础上，所述滚动优化设计包括如下步骤：

步骤①：检测ktp时刻整流器输入电流的有效值i2(k)、整流器输出电压uo(k)和电流io(k)；

步骤②：初始化控制变量m(i)(i＝1)，根据式(12)计算预测输出电压uoⁱ(k+1)，再通过式(13)计算成本函数j(i)；

步骤③：判断滚动优化次数i是否达到预定次数n，若达到，用冒泡排序法求出j(i)的最小值jmin(i)，若未到，则i＝i+1，返回步骤②；

步骤④：由成本函数最小值jmin(i)，找出最优的控制变量和在k时刻整流器移相角β；

使用所述的基于恒压输出的效率优化控制方案：基于mpc调节整流器输入端等效负载后，从控制逆变器的角度入手优化系统效率；

基于有源整流器的s-s补偿ipt系统中，若忽略开关损耗，系统效率表示为：

其中，pin是系统输入功率，pout是系统输出功率，ploss是线圈损耗，rp1是发射线圈寄生电阻，rp2是接收线圈寄生电阻，在恒定输出功率和输出电压的情况下，发射线圈电流i1和接收线圈电流i2：

忽略线圈损耗，发射线圈电流和接收线圈电流可以简化为：

根据式(14)，计算最高效率情况下发射线圈电流和接收线圈电流之间的关系：

将式(17)、(18)代入(19)，解出最大传输效率时，逆变器移相角α与整流器移相角β之间的关系：

实施例5

在实施例一的基础上，所述效率优化控制方案包括如下步骤：

步骤1)：检测初始时刻逆变器输入电流id(0)，初始化逆变器移相角α(0)和逆变器移相角增量δα；

步骤2)：在下个采样时刻，将上一时刻的逆变器移相角与移相角增量相加，得到当前逆变器移相角α(1)＝α(0)+δα，并测量此刻的逆变器输入电流id(1)；

步骤3)：根据id(0)和id(1)的大小关系决定扰动观察的方向，若id(1)<id(0)，用α(k+1)＝α(k)+δα来增加α以靠近最佳的逆变器移相角，反之则用α(k+1)＝α(k)-δα来减小α，其中k表示采样时间ktr，tr是逆变器的相位角控制的控制周期；

步骤4)：对于观察扰动的两个方向，将采样时间k+1处的副边电流i2(k+1)与前一个采样时间k处的副边电流i2(k)进行比较，同时比较采样时间k+1处输出电压uo(k+1)与参考电压的差值是否小于参考误差rlim；如果i2(k+1)<i2(k)且|uo(k)-uset|<rlim，则α(k+1)＝α(k)+δα或α(k+1)＝α(k)-δα应持续进行以使α逼近最优的移相角；若i2(k+1)>i2(k)或|uo(k)-uset|>rlim，则意味着α的变化不能进一步降低副边电流，α(k)可以被认为是最优的移相角，相应的是i2(k)是最小副边电流i2min。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。