混沌信号生成方法、电路、调制信号输出电路及开关电源与流程

本发明涉及自动控制技术领域，尤其涉及一种混沌信号生成方法、电路、调制信号输出电路及开关电源。

背景技术：

开关电源具有优异的性能，被广泛应用于各种供电场合。现有技术中还将混沌电力电子变换器用于开关电源的调制方面，从而抑制开关电源的emi，达到更佳的供电效果。但由于混沌信号中不同参数的混沌吸引子对emi的抑制效果均不相同，现有技术的缺点在于未使用最优的混沌吸引子，从而使得emi的抑制效果仍存在提高空间。

技术实现要素：

为了解决上述至少一个技术问题，本发明的目的在于提供一种混沌信号生成方法、电路、调制信号输出电路及开关电源。

一方面，实施例中包括一种混沌信号生成方法，包括以下步骤：

设定混沌模型的工作参数，使得设定后的所述工作参数对应的李雅普诺夫指数达到极大值；

使用经过设定的所述混沌模型生成混沌信号。

进一步地，所述设定混沌系统的工作参数，使得设定后的所述工作参数对应的李雅普诺夫指数达到极大值这一步骤，具体包括：

选定所述工作参数的调整区间；

在所选定的调整区间内，计算各所述工作参数对应的李雅普诺夫指数；

根据计算出的各所述李雅普诺夫指数中的最大值，查找对应的工作参数；

使用查找出的所述工作参数，对所述混沌系统进行设定。

进一步地，所述混沌模型为蔡氏混沌模型、刘氏混沌模型或洛伦兹混沌模型。

进一步地，所述混沌模型为蔡氏混沌模型：

式中a、b、α和β为所述蔡氏混沌模型的工作参数，且a＝6。

进一步地，所述混沌模型为刘氏混沌模型：

式中a、b、c、k和h为所述刘氏混沌模型的工作参数，且a＝25。

进一步地，所述混沌模型为洛伦兹混沌模型：

式中a、b和r为所述洛伦兹混沌模型的工作参数，且a＝25。

另一方面，实施例中还包括一种混沌信号生成电路，其用于使用实施例所述混沌信号生成方法生成并输出混沌信号。

另一方面，实施例中还包括一种调制信号输出电路，包括：

实施例所述的混沌信号生成电路；

pwm发生电路，其设有频率控制端口，用于通过所述频率控制端口接收所述混沌信号生成电路输出的混沌信号，并根据所述混沌信号生成并输出pwm调制信号。

另一方面，实施例中还包括一种开关电源，包括：

实施例所述的调制信号输出电路；

开关拓扑电路，用于获取所述调制信号输出电路输出的pwm调制信号，在所述pwm调制信号的调制下输出电压和电流。

进一步地，所述开关拓扑电路为buck电路、boost电路、buck/boost电路或反激变换电路。

本发明的有益效果是：根据李雅普诺夫指数来选择合适的混沌模型工作参数，当选择对应李雅普诺夫指数局部或全局最大值的工作参数时，混沌模型所输出的混沌信号具有局部或全局最小的方差，此时混沌信号的频谱分布均匀，有助于emi的能量扩散，使用这样的混沌信号来进行开关电源的调制，能够取得较佳的emi抑制效果。

附图说明

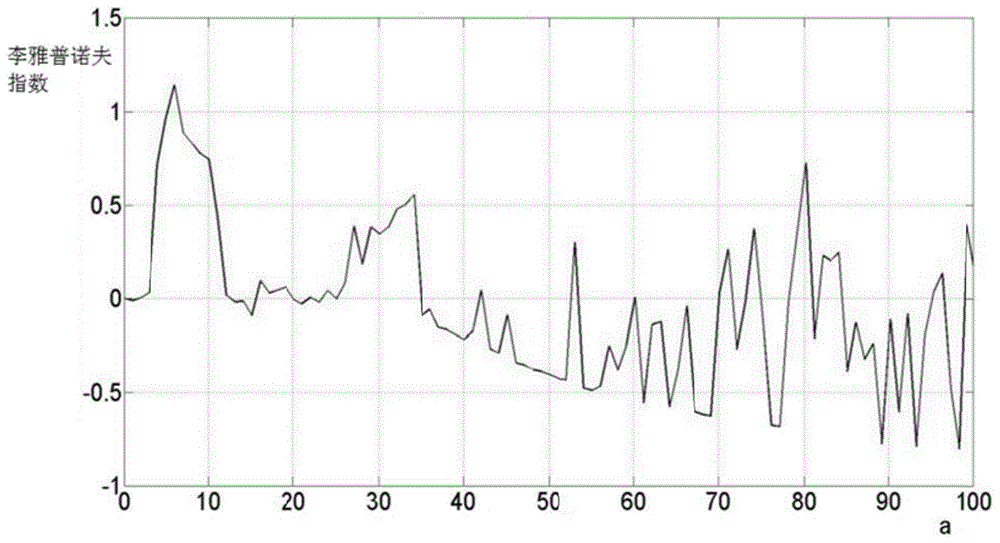
图1为蔡氏混沌模型的工作参数a与李雅普诺夫指数的对应关系图；

图2为刘氏混沌模型的工作参数a与李雅普诺夫指数的对应关系图；

图3为洛伦兹混沌模型的工作参数a与李雅普诺夫指数的对应关系图；

图4为实施例中蔡氏混沌模型所生成混沌信号的频谱图；

图5为实施例中刘氏混沌模型所生成混沌信号的频谱图；

图6为实施例中洛伦兹混沌模型所生成混沌信号的频谱图；

图7为实施例中调制信号输出电路的结构框图；

图8为实施例中开关电源的结构框图；

图9为实施例中对开关电源进行仿真所使用的开关拓扑电路；

图10为基于蔡氏混沌模型的开关电源输出的干扰信号的fft图像；

图11为基于刘氏混沌模型的开关电源输出的干扰信号的fft图像；

图12为基于洛伦兹混沌模型的开关电源输出的干扰信号的fft图像。

具体实施方式

为了更清楚地说明本发明的实施方法以及解决的技术问题，下面结合附图和实施例作进一步说明。

实施例1

常用的混沌模型包括蔡氏混沌模型、刘氏混沌模型和洛伦兹混沌模型。其中蔡氏混沌模型(chua’s)的数学表达式为：

式中a、b、α和β为所述蔡氏混沌模型的工作参数。

刘氏混沌模型(liu)的数学表达式为：

式中a、b、c、k和h为所述刘氏混沌模型的工作参数。

洛伦兹混沌模型(lorenzx)的数学表达式为：

式中a、b和r为所述洛伦兹混沌模型的工作参数。

李雅普诺夫指数(lyapunovexponent)表示相空间相邻轨迹的平均指数发散率的数值特征，是用于识别混沌运动若干数值的特征之一。针对蔡氏混沌模型、刘氏混沌模型和洛伦兹混沌模型中的工作参数a进行研究，分别计算它们的工作参数a的李雅普诺夫指数，计算结果分别如图1、图2和图3所示。

由图1可以看到，在蔡氏混沌模型的工作参数a的常用区间[10，20]内，a与其李雅普诺夫指数呈反向变动关系；由图2可以看到，在刘氏混沌模型的工作参数a的常用区间[10，30]内，a与其李雅普诺夫指数呈正向变动关系；由图3可以看到，在洛伦兹混沌模型的工作参数a的常用区间[10，30]内，a与其李雅普诺夫指数呈正向变动关系。

图4是蔡氏混沌模型中的参数分别取a＝6、a＝10和a＝16时，蔡氏混沌模型所生成的混沌信号中的x分量的频谱。通过计算可知，a＝6时，x分量的方差为3.25e-3；a＝10时，x分量的方差为4.78e-3；a＝16时，x分量的方差为4.18e-3。

图5是刘氏混沌模型中的参数分别取a＝10、a＝16和a＝25时，刘氏混沌模型所生成的混沌信号中的x分量的频谱。通过计算可知，a＝10时，x分量的方差为1.08e-4；a＝16时，x分量的方差为1.15e-4；a＝25时，x分量的方差为1.00e-4。

图6是洛伦兹混沌模型中的参数分别取a＝10a＝20和a＝25时，洛伦兹混沌模型所生成的混沌信号中的x分量的频谱。通过计算可知，a＝10时，x分量的方差为3.76e-4；a＝20时，x分量的方差为3.18e-4；a＝25时，x分量的方差为3.08e-4。

由图1-图6，可以总结出一个规律：对于同一混沌模型，调整其工作参数，如果该工作参数对应的李雅普诺夫指数越大，那么使用该工作参数生成的混沌信号的方差越小，即频谱分布越均匀。而在频域上均匀分布的混沌信号有助于emi的能量扩散。

根据上述分析结果，可以确定：根据李雅普诺夫指数来选择混沌模型的工作参数，能够获得有益效果。

本实施例中的混沌信号生成方法包括以下步骤：

s1.设定混沌模型的工作参数，使得设定后的所述工作参数对应的李雅普诺夫指数达到极大值；

s2.使用经过设定的所述混沌模型生成混沌信号。

所述步骤s1具体包括：

s101.选定所述工作参数的调整区间；

s102.在所选定的调整区间内，计算各所述工作参数对应的李雅普诺夫指数；

s103.根据计算出的各所述李雅普诺夫指数中的最大值，查找对应的工作参数；

s104.使用查找出的所述工作参数，对所述混沌系统进行设定。

步骤s1中的所述极大值是指在特定的调整区间内，各所述工作参数对应的李雅普诺夫指数所取得的最大值。如果不对工作参数选定特定的调整区间，也就是考虑工作参数的所有取值范围，那么此时步骤s1中就是以“对应李雅普诺夫指数达到最大值”为所述工作参数的选择条件。

实施例2

本实施例中的混沌信号生成电路，在生成混沌信号前先执行实施例1中的步骤s1和s2，以确定合适的混沌模型的工作参数，从而使用该合适的工作参数来生成并输出混沌信号。

根据实施例1中的原理说明可知，本实施例中的混沌信号生成电路所输出的混沌信号具有局部或全局方差最小、频域分布最均匀等特点，将该混沌信号用于开关电源，有助于emi的能量扩散，取得更佳的emi抑制效果。

实施例3

参照图7，本实施例中的调制信号输出电路由pwm发生电路和实施例2中所述的混沌信号生成电路组成，其中pwm发生电路上设有频率控制端口。将混沌信号生成电路所生成的混沌信号输入到pwm发生电路的频率控制端口，pwm发生电路根据接收到的混沌信号来生成并输出pwm调制信号。

根据实施例1和实施例2中的原理说明可知，实施例2中的混沌信号生成电路所输出的混沌信号具有局部或全局方差最小、频域分布最均匀等特点，将该混沌信号用于本实施例中的pwm发生电路，并将该pwm发生电路生成的pwm调制信号用作开关电源的调制，有助于emi的能量扩散，取得更佳的emi抑制效果。

实施例4

参照图8，本实施例中的开关电源由开关拓扑电路和实施例3中所述的调制信号输出电路组成。其中，所述开关拓扑电路可以是buck电路、boost电路、buck/boost电路或反激变换电路。使用所述调制信号输出电路输出的pwm调制信号来对开关拓扑电路进行调制，从而实现开关电源的功能。

根据实施例1、实施例2和实施例3中的原理说明可知，实施例2中的混沌信号生成电路所输出的混沌信号具有局部或全局方差最小、频域分布最均匀等特点，将该混沌信号用于实施例3中的pwm发生电路，并将该pwm发生电路生成的pwm调制信号用作本实施例中开关拓扑电路的调制，有助于emi的能量扩散，取得更佳的emi抑制效果。

使用仿真软件saber来搭建实施例4中的开关电源，其中所使用的开关拓扑电路为如图9所示的反激变换电路。

图10是以蔡氏混沌模型所输出的混沌信号(x分量)为基础进行调制，所述开关电源所输出的信号中包含的电磁干扰信号的fft图像，图10中三部分分别对应工作参数a＝6、a＝10和a＝16。由图10可知，当a＝6时，电磁干扰信号的频域分布较宽，即emi的抑制效果较佳。此时，蔡氏混沌模型的其他工作参数的取值分别为b＝17.23、α＝-1.368、和β＝-0.738。

图11是以刘氏混沌模型所输出的混沌信号(x分量)为基础进行调制，所述开关电源所输出的信号中包含的电磁干扰信号的fft图像，图11中三部分分别对应工作参数a＝10、a＝16和a＝25。由图11可知，当a＝25时，电磁干扰信号的频域分布较宽，即emi的抑制效果较佳。此时，刘氏混沌模型的其他工作参数的取值分别为b＝40、c＝2.5、k＝1和h＝4。

图12是以洛伦兹混沌模型所输出的混沌信号(x分量)为基础进行调制，所述开关电源所输出的信号中包含的电磁干扰信号的fft图像，图12中三部分分别对应工作参数a＝10、a＝20和a＝25。由图12可知，当a＝25时，电磁干扰信号的频域分布较宽，即emi抑制效果较佳。此时，洛伦兹混沌模型的其他工作参数的取值分别为和r＝28。

图10-图12的仿真结果表明实施例1中所提供的技术方案是可靠的，即选用对应局部或全局最大李雅普诺夫指数的工作参数来生成混沌信号，再使用这样的混沌信号来进行调制，能够取得较佳的emi抑制效果。

以上是对本发明的较佳实施进行了具体说明，但对本发明创造并不限于所述实施例，熟悉本领域的技术人员在不违背本发明精神的前提下还可做作出种种的等同变形或替换，这些等同的变形或替换均包含在本申请权利要求所限定的范围内。