基于未知输入观测器的降压型直流变换器非奇异终端滑模控制方法与流程

本发明属于降压型直流变换器滑模控制方法的技术领域，特别涉及一种基于未知输入观测器的降压型直流变换器非奇异终端滑模控制方法。

背景技术：

直流开关变换器主要是通过对功率开关进行高频的导通和关断实现电能在输入和输出端的传输。那么如何能够使直流开关变换器以更高的效率转换成更高品质的电能是当代电力电子技术面临的一大问题。为了实现这一目的，通常会选择两种方式，一种是通过采用各种形式的软开关变换电路或者降低内阻等方法来减小变换器中开关造成的损耗；另一种是使用各种新型的控制方法来提高变换器的各项动态性能指标和稳态精度。这里所述的控制方法包括模糊控制、鲁棒控制、神经网络控制、自适应控制和滑模变结构控制等非线性控制方法。其中滑模变结构控制方法有着方法简洁，鲁棒性强及响应速度快等优点，能够较好地改善系统的动态性能。

另外，由于系统外部扰动以及模型参数不确定导致的系统干扰，许多学者开始专注于基于扰动估计的复合控制方法，其中基于扰动观测器对系统进行前馈补偿的方法是效果比较理想的一种，其优点在于可以不牺牲系统性能，只需要对估计出来的扰动进行前馈补偿便可以消除扰动导致的系统稳态精度差等问题。如公开号为cn104601071a的中国专利公开了一种基于扰动观测器的永磁同步电机电流环滑模控制方法，通过构建一个多输入多输出的滑模控制器，利用多输入量之间存在耦合的关系，实现电流环的解耦跟踪控制，使电流控制内环只有一个控制器，即滑模控制器。同时考虑到当外界干扰和系统参数变化时，滑模变结构控制的鲁棒性就会减弱，因此为了进一步提高系统的鲁棒性，在控制策略中加入了一个扰动观测器，用于在线预估系统由于参数变化和外界干扰引起的不确定量，补偿到滑模控制器，实现系统电流的误差补偿，确保了电流精确控制，提高了永磁同步电机速度调节性能。

因此，目前本领域技术人员主要集中在解决由于实际电路中存在输入电压波动、输出负载突变以及电感，电容参数摄动等扰动，造成的使用降压型直流变换器有可能出现输出电压不稳定，误差大等不理想情况。

技术实现要素：

本发明的目的在于提供一种基于未知输入观测器的降压型直流变换器非奇异终端滑模控制方法，该控制方法在非奇异终端滑模控制器的基础上利用未知输入观测器对扰动进行观测，估计系统的集总扰动，并通过滑模控制器进行前馈补偿，使得最后系统能够快速稳定地输出理想电压。

为了解决上述技术问题，本发明提出的技术方案为：

一种基于未知输入观测器的降压型直流变换器非奇异终端滑模控制方法，所述控制方法包括以下步骤：

(1)建立降压型直流变换器系统模型，初始化系统状态及控制参数；

(2)设计未知输入观测器，估计系统的集总扰动，未知输入观测器的估计误差在有限时间内收敛到平衡点邻域附近；

(3)根据系统的集总扰动设计非奇异终端滑模控制器，控制降压型直流变换器系统输出稳定的电源电压。

本发明的技术构思为：针对降压型直流变换器系统中滑模控制的收敛速度问题以及扰动造成的影响，本发明采用未知输入观测器，并基于该观测器设计非奇异终端滑模控制器，与传统的滑模控制相比，系统能更快地在有限时间内收敛到平衡，且具有更高的稳态精度。

在步骤(1)中，所述降压型直流变换器系统模型表示成如下形式：

降压型直流变换器的系统模型表示成如下形式：

其中，vo是输出电压，vin0是输入电压的标称值，il是电感电流，l0、c0、r0分别是电路中电感、电容和负载电阻的标称值；u是控制输入。

在步骤(1)中，初始化系统状态及控制参数的过程为：

定义状态变量x1＝vo-vref，则降压型直流变换器误差动态方程写成如下状态空间形式：

其中，vref为期望参考输出电压，d1(t)是系统的集总扰动；这里l、c、r分别是电感、电容和负载电阻的实际值，vin是实际输入电压。

在步骤(2)中，所述设计未知输入观测器的过程为：

定义滤波变量x1f,x2f,uf,d1f，系统(2)可改写为：

其中，x1f,x2f,uf,d1f分别为x1,x2,u,d1经过低通滤波后的信号。它们满足：

其中，k是滤波时间常数；

将式(4)带入式(3)可得

通过选取合适的k值，可以使得d1f近似于系统集总扰动d1，由此可以估计得到d1的近似值；

由此可以设计得到未知输入扰动观测器如下：

在步骤(2)中，观测器误差收敛性证明：

通常假设系统集总扰动d1以及系统集总扰动导数有界，满足其中d1^*为扰动d1的上界，为扰动一阶导数的上界，

定义观测器估计误差：

将(6)代入式(7)中，可得：

构造李雅普诺夫函数：

对其求导得：

将式(2)和式(4)代入得到：

解上述微分方程可得：

由式(12)可得，能够在有限时间内收敛到平衡点邻域附近。在步骤(3)中，所述非奇异终端滑模控制器的设计过程如下：(3-1)设计非奇异终端滑模

其中，1＜p/q＜2，0＜λ＜1；

滑模控制器设计如下：

其中，η＞0为控制器参数，sign为符号函数；

(3-2)构造李雅普诺夫函数：

对其求导，得：

由式(12)可知，有界，只要参数η取值满足即可证明该系统稳定。

在本发明中，作为一个控制闭环系统而言，u为滑模控制方法中设计的控制器，也可以理解为一个控制信号，作为一个控制输入端对buck变换器起到控制效果。因此，u可以表示控制输入和滑模控制器。

本发明采用非奇异终端滑模模控制方法，设计非奇异终端滑模控制器，实现降压型直流变换器输出电压的快速调节。

本发明的有益效果为：实现系统输出电压在受到扰动的情况下也内快速恢复稳定输出期望参考输出电压，减弱了扰动对系统造成的影响。

附图说明

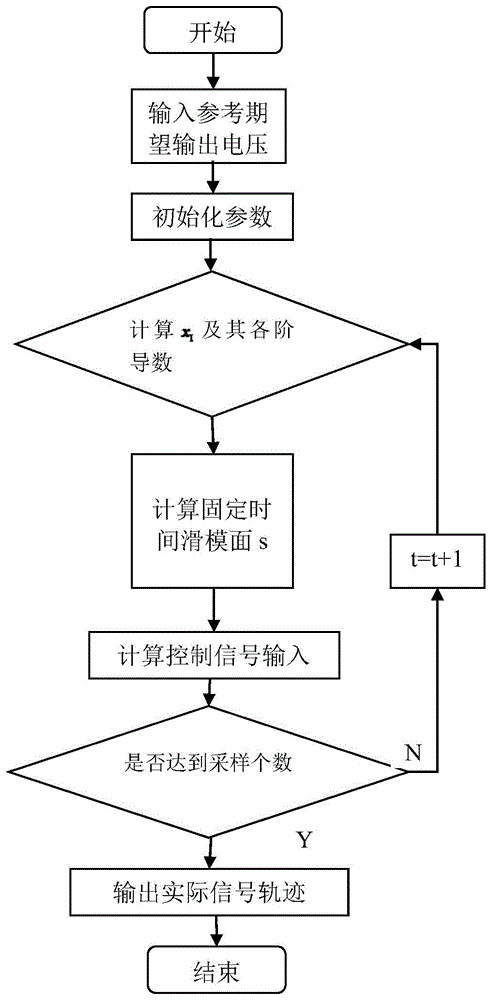
图1为本发明的控制方法的流程图；

图2为电路负载在时间t＝0.1s时，电路负载发生突变由10ω升高为12ω，在时间t＝0.2s时电路负载又由12ω降低到9ω，本发明的控制系统输出电压响应曲线；

图3为电路负载在时间t＝0.1s时，电路负载发生突变由10ω升高为12ω，在时间t＝0.2s时电路负载又由12ω降低到9ω，本发明的控制系统电感电流响应曲线。

具体实施方式

下面结合附图对本发明做进一步说明。

参照图1-图3，本实施例提供的基于未知输入观测器的降压型直流变换器非奇异终端滑模控制方法包括以下步骤：

步骤1，建立降压型直流变换器系统模型，初始化系统状态及控制参数，过程如下：

1.1，降压型直流变换器的系统模型表示成如下形式：

其中，vo是输出电压，vin0是输入电压的标称值，il是电感电流，l0、c0、r0分别是电路中电感、电容和负载电阻的标称值；u是控制输入；

1.2，定义状态变量x1＝vo-vref，则降压型直流变换器误差动态方程写成如下状态空间形式：

其中，vref为期望参考输出电压，d1(t)是系统的集总扰动。

这里l、c、r分别是电感、电容和负载电阻的实际值，vin是实际输入电压。

步骤2，设计未知输入观测器，过程如下：

2.1，定义滤波变量x1f,x2f,uf,d1f，系统(2)可改写为：

其中，x1f,x2f,uf,d1f分别为x1,x2,u,d1经过低通滤波后的信号。它们满足：

其中，k是滤波时间常数。

将式(4)带入式(3)可得：

通过选取合适的k值，可以使得d1f近似于系统集总扰动d1，由此可以估计得到d1的近似值。由此可以设计得到未知输入扰动观测器如下：

2.2，观测器误差收敛性证明

通常假设扰动d1以及扰动导数有界，满足supt≥0d1≤d1^*，其中d1^*为扰动d1的上界，为扰动一阶导数的上界，

定义观测器估计误差：

将式(6)代入式(7)中，可得：

构造李雅普诺夫函数：

对其求导得：

将式(2)和式(4)代入得到：

解上述微分方程可得：

由式(12)可得，能够在有限时间内收敛到平衡点邻域附近。

步骤3，非奇异终端滑模控制器设计，过程如下：

3.1，设计非奇异终端滑模：

其中，1＜p/q＜2，0＜λ＜1；

滑模控制器设计如下：

其中，η＞0为控制器参数，sign为符号函数。

3.2，构造李雅普诺夫函数：

对其求导，得：

由式(12)可知，有界，只要参数η取值满足即可证明该系统稳定。

为验证所提方法的有效性，本实施例对由式(14)表示的滑模控制器的控制效果进行仿真实验，设置仿真实验中的初始条件与部分参数，即：系统模型中，l0＝10mh，c0＝1000μf，r0＝10ω，vref＝5v。控制参数为k＝0.001，λ＝0.2，η＝100，p/q＝0.85。

图2为同参数情况下，非奇异终端滑模与传统滑模进行的对比，在时间t＝0.1s时，电路负载发生突变由10ω升高为12ω，在时间t＝0.2s时电路负载又由12ω突然降低到9ω，可以观察到，即使负载发生突变，系统也能够迅速做出反应并且输出稳定的期望参考电压，并且相比于传统滑模，非奇异终端滑模的响应时间较短，恢复稳定的速度较快，有更好的鲁棒性。图3为相同条件的电感电流的仿真图，同样可以观察得到，基于未知输入扰动观测器的非奇异终端滑模具有较好的效果。

以上阐述的是本发明给出的一个实施例表现出的优良优化效果，显然本发明不只是限于上述实施例，在不偏离本发明基本精神及不超出本发明实质内容所涉及范围的前提下对其可作种种变形加以实施。所提出的控制方案对降压型直流变换器是有效的，在所提出的控制器的作用下，实现降压型直流变换器输出电压在有限时间内快速收敛。