一种基于最优控制的双电机消隙方法及系统与流程

本发明涉及机电控制领域，具体涉及一种基于最优控制的双电机消隙方法及系统。

背景技术：

目前多台电机共同驱动是大惯量伺服系统的主要实现途径，它被广泛运用在工业、农业、军事装备等领域，比如应用在大型高精度雷达伺服、火炮伺服、重型机床回转工作台、射电望远镜等高精度跟踪设备上。在多电机驱动控制领域，为了获得大转矩、低转速的效果，常采用齿轮传动。齿轮传动过程中存在齿隙，而齿隙的存在严重影响伺服系统的定位精度、降低系统工作带宽、使设备产生抖动，给系统带来较大的稳态误差。

齿隙非线性的本质是一种非线性位置误差，它存在于传动齿轮或传动链之间、电机与减速器之间。在力矩的传动过程中，非线性变化的齿隙总使得负载侧的输出位移和速度与期望值产生偏差，导致跟随性能大打折扣。刚性强的主齿轮在反向运转时会与从动齿轮产生碰撞并伴随着剧烈的振动和噪音。因此为保证系统的稳定性，齿隙补偿有意义。

为了减小间隙影响的办法传统上有机械消隙和电消隙两种方法。机械消隙法包括双片齿轮错齿消隙、扭力杆消隙等，它们实现复杂、可靠性差。电消隙法是在电机上施加偏置力矩，例如西安电子科技大学的研究员提出的变值偏置力矩消隙法，但该偏置力矩的补偿数值在不同的齿轮间隙存在时间段内是一个恒定值，该力矩补偿曲线在实际应用中不能补偿齿隙角的动态变化，不能完全消除齿合齿隙对传动系统造成的间歇性影响。因此需要对施加的偏置力矩的力矩补偿曲线进行优化，使偏置力矩尽可能跟随齿隙角运动状态的改变进行改变偏置力矩的大小，在保证能完成跟踪的情况下，降低偏置力矩所消耗的能量。

技术实现要素：

1、所要解决的技术问题：

针对上述技术问题，本发明提出一种基于最优控制的双电机消隙方法及系统，本方法从齿轮传动系统中的运行机理入手，根据最优控制中的时间最优控制理论，得出负载转角达到相应标准的最短时间，并用神经网络逼近时间性能指标，得出最短时间内传动系统的控制量的变化范围，从而确定电流的设定值。相比工程上的经验数值，该电流设定值更加精确能够在实现负载跟踪的前提下，消除齿隙非线性的影响并且保证电机间的同步。

2、技术方案：

一种基于最优控制的双电机消隙方法，其特征在于：齿隙消除器进行消隙的过程具体包括以下步骤：

步骤一：对电机传动链的机理进行分析，建立齿轮间隙的电机传动系统模型。

步骤二：结合电机传动系统模型和时间最优控制原理，得到消隙器里的电流设定值。

步骤三：如果电机的伺服驱动器中的驱动电流小于步骤二中的电流设定值时，那么此时的电机传动系统处于齿隙状态，进行步骤四。

步骤四：结合电机传动系统模型和能量最优控制原理，得到消隙器里的转换函数；驱动器向电机输入的电流经过消隙器里的转换函数，随着齿轮间隙角的增大快速增大，通过消隙器反馈给驱动器，使齿轮快速穿过齿隙。

进一步地，所述步骤一具体包括以下步骤：

s11:根据电机与负载之间的输入与输出关系，建立电机传动系统内部方程；

式(0)中cedn、θdn、idn、rdn、ldn、udn分别为第n台电机的反电动势系数、转角、电阻、电流、电感、电压。kdn、jdn、bdn、mdn、mxcn、i1分别为第n台电机的力矩系数、转动惯量系数、等效粘性摩擦系数、第n台电机轴的电磁转矩、与第n台电机轴所对应的第n个小齿轮的转矩、第n台电机与第n个小齿轮之间的传动比。jxcn、bxcn、mxcdcn分别为与第n台电机轴所对应的第n个小齿轮的转动惯量系数、等效粘性摩擦系数、第n个小齿轮和与之对应的第n个大齿轮之间的弹性力矩。θxcn、θdcn、i2、kxcdcn分别为第n个小齿轮的转角、第n个大齿轮的转角、第n个小齿轮和与之对应的第n个大齿轮之间的传动比、第n个小齿轮和与之对应的第n个大齿轮之间的传动刚度。jdcn、bdcn、mdcn、mf分别为第n个大齿轮的转动惯量系数、等效粘性摩擦系数、第n个大齿轮的转动力矩、末端负载的转矩。jf、bf、kf、θf、tf分别为末端负载的转动惯量系数、等效粘性摩擦系数、传动刚度、末端负载的转角、末端负载与大齿轮之间的弹性力矩。

s12:由于受齿轮间隙非线性的影响，大小齿轮间隙函数为死区函数，具体表达式为：

上式中，θxcn、θdcn、i2、kxcdcn分别为第n个小齿轮的转角、第n个大齿轮的转角、第n个小齿轮和与之对应的大齿轮之间的传动比、第n个小齿轮和与之对应的大齿轮之间的传动刚度；(θxcn-i2θdcn)为大小齿轮间的位置差。

s13:建立电机端电压与齿轮间隙的关系；具体为：令α＝k3udn，其中k3为大齿轮与小齿轮之间的齿轮间隙系数，上面(1)式转换为：

定义齿轮间隙变量

θxcn-i2θdcn≥+k3udn

-k3udn<θxcn-i2θdcn<+k3udn

θxcn-i2θdcn≤-k3udn

得出大小齿轮间的齿隙表达式：

对电机内部传动方程按照输入输出关系进行连接，得出含有齿隙的小齿轮和端电压的状态方程与含有齿隙的大齿轮和端电压的状态方程：

其中k1表示末端负载与大齿轮之间弹性力矩的力矩系数；

为了便于处理，将上面的两个状态方程进行处理得出式(4)与(5)；即把小齿轮和端电压状态方程中的系数矩阵分成两行两列的方阵，得到小齿轮和端电压与大齿轮和端电压的关系，如下式：

(4)式与(5)式中，kdn、jdn、bdn、i1分别为第n台电机的力矩系数、转动惯量系数、等效粘性摩擦系数、第1台电机和与之对应的小齿轮间的传动比；jxcn、bxcn分别为与第n台电机轴所对应的第n个小齿轮的转动惯量系数、等效粘性摩擦系；θxcn、i2、kxcdcn分别为第n个小齿轮的转角、第2个小齿轮和与之对应大齿轮之间的传动比、第n个小齿轮和与之对应的大齿轮之间的传动刚度；jdcn、bdcn分别为第n个大齿轮的转动惯量系数、等效粘性摩擦系数；jf、bf、θf分别为末端负载的转动惯量系数、等效粘性摩擦系数、末端负载的转角；k1表示末端负载与大齿轮之间弹性力矩的力矩系数，k3为大齿轮与小齿轮之间的齿轮间隙系数。

进一步地，步骤二具体包括以下步骤：

s21:为了使控制系统在最短的时间内完成要求，采用最优控制的时间性能指标；时间性能指标公式为：

(6)式中j表示时间性能指标；xt2表示t2时刻的状态；根据控制系统应该满足的位置值、速度值，求解状态方程得出最优的时间性能指标。

s22:求解小齿轮穿越齿隙所需要的时间性能指标：

其中含有小齿轮的微分方程为：

(7)式中c1、c2为微分参数，小齿轮换向时的角速度：

(8)式中

当电机轴正传时：

当电机轴反转时：

取tf-t0作为小齿轮换向过程中，为克服齿轮间隙的时间性能指标，记为

s23:求解大齿轮穿越齿隙所需要的时间性能指标：

含有大齿轮的微分方程：

其中c3、c4为微分参数，大齿轮换向时的角速度：

式(11)中：

当小齿轮正传时：

当小齿轮反转时：

其中表示小齿轮开始转动与小齿轮带动大齿轮转动时，t0时刻所对应的的角速度值；表示小齿轮开始转动与小齿轮带动大齿轮转动时，tf时刻所对应的的角速度值。

取t'f-t'0作为大齿轮换向过程中，克服齿轮间隙的时间性能指标，记为

s24:求得消隙器里的电流设定值：

因为电机小齿轮自身转角与大齿轮、大齿轮自身转角与负载是一体联动的，所以取两部分消耗的最短时间作为传动系统克服齿轮间隙的时间性能指标即：w为神经网络权重，ε为估计误差，用神经网络逼近最优控制的时间指标：

由式(13)得消隙控制器的电流设定值：预设误差存在允许的误差范围、控制量udn以及对应的isn的误差范围，取误差范围的头尾值is1、is2作为消隙器的电流设定值。

进一步地，步骤四具体包括：

s41:为使控制系统消耗能量最少，需满足能量性能指标：

为了使能量性能指标最小，用最小值原理并结合控制系统的状态方程来构造哈密顿函。

哈密顿函数的一般表达式由状态过程量和控制系统的状态方程所组成，如式(16)

由极小值原理知，当h(x，u，λ)最小时，性能指标j达最小；同时使h(x，u，λ)min成立的条件是h(x，u，λ)中的λbu达最小；式(16)中a、b为中的固定系数矩阵，所以使h(x，u，λ)min，必须使λ与u取到最小且λ与u符号要相反；对哈密顿求偏导数，得协态方程即状态方程中控制律u的符号为-sgn{λ·b}＝-sgn{e^-at·b}；因为λ与u符号相反，所以λu为负数，h(x，u，λ)min取得到，能量性能指标jmin取得到。

根据与极小值原理等价的古典变分法知：当时，哈密顿函数h(x，u，λ)取最小值，能量性能指标j也取最小值；因为公式(16)，所以当时，h(x，u，λ)取最小，状态方程中控制律u的数值为

s42：由小齿轮和端电压即式(4)与大齿轮和端电压即式(5)的关系得到齿轮间隙状态方程：

将齿隙状态方程即式(17)中的系数矩阵带入一般控制律u得齿隙控制律udn的符号与数值：

式(18)中λ1与λ2的取值决定能量最优控制律udn的符号，而式(18)与式(19)共同决定能量最优控制律udn的数值大小；

然后求解大小齿轮的齿隙微分方程：

其中c5、c6为微分参数，大小齿轮间的齿隙角度：

式(21)中

当电机正传或反转时，传动齿轮的齿隙表达式为：

在双电机传动系统中，消除齿轮间隙的转换函数设置为：

s43：根据能量最优理论优化齿轮间隙的电流驱动曲线：

通过齿隙表达式(23)，可以得到双电机驱动电流表达式：

进一步地，还包括速度控制器调节速度；所述速度控制器用调节未知扰动引起的速度偏差，保证系统稳定性；具体包括以下步骤：

s51：设计基于变结构理论的速度积分滑模面；

设定位置控制器输出值即给定的电机速度与电机的反馈速度分别为w^*、w，则电机的实际速度偏差△为w^*-w，设计滑模面：滑模面含误差的积分项和指数项，它们能在一定的时间内使误差快速收敛，保证系统稳定性。

s52：对式(26)求导，得出改进一般的滑模趋近律：

当一般控制系统从滑模面运动到终末状态，即时，此时s＝0，系统恢复稳定，

当一般控制系统从滑模面运动到终末状态，即时，此时s＝q，系统才稳定，

一种基于最优控制的双电机消隙系统，包括速度控制器、消隙器、pid位置控制器、控制n台电机的减速机相连的n台伺服驱动器、n台装有编码器的伺服电机、n台每台分别连接一台伺服电机的减速机以及负载；各电机与减速机的速度传输至速度控制器，速度控制器将传速度偏差值传输至各个电机对驱动电流进行判断，如果驱动电流小于设定值，则进行步骤四，消隙控制器向驱动器输入电流，实现动态的增大驱动电流，使齿隙快速缩短；位置控制器是用来调整给定位置与负载末端实际位置之间的位置偏差。

3、有益效果：

(1)本发明对传统双电机伺服系统重新建模，推导出输入端电压与末端负载转动角度之间的状态方程，增强传动系统闭环控制的稳定性。

(2)本发明中的消隙控制器，通过时间最优控制并结合神经网络来给定消隙器内部的电流设定值，由传动系统机理推导出的电流设定值比工程中的经验数值更加准确。

(3)本发明中把含有齿隙的传动系统与能量最优控制相结合，推导出新型消隙切换函数。相比传统等腰梯形式的切换函数，消隙转矩能根据传动系统的实际齿隙情况去动态补偿，减少能量损失。

(4)本发明对基于一般趋近律的速度控制器进行优化，在趋近律上添加指数项和幂次趋近项。当运行过程中出现干扰时，减少因扰动而产生的抖振现象，提升系统的快速性与准确性。

附图说明

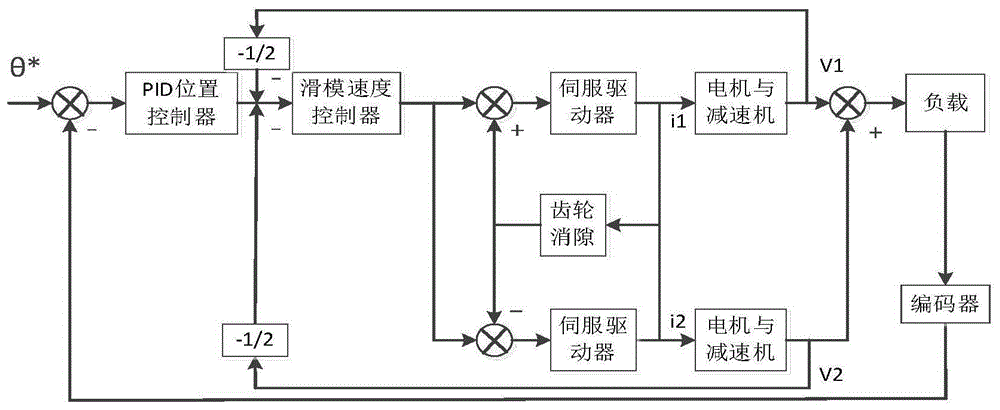
图1为本发明的双电机传动系统的控制结构图；

图2为本发明的双电机传动系统的机械结构图；

图3为本发明的新型切换函数表示图；

图4为具体实施方式中偏置力矩输入输出图。

具体实施方式

如附图1至4所示，本发明设计了双电机传动系统的消隙控制器和速度控制器。根据输入电压与输出负载的关系，推导出传动系统状态方程，采用最优控制里的时间最优原理整定消隙控制器的电流设定值，采用能量最优控制原理优化控制器的转换函数。优化滑模趋近律，设计速度控制器。

一种基于最优控制的双电机消隙方法，其特征在于：齿隙消除器进行消隙的过程具体包括以下步骤：

步骤一：对电机传动链的机理进行分析，建立齿轮间隙的电机传动系统模型。

步骤二：结合电机传动系统模型和时间最优控制原理，得到消隙器里的电流设定值。

步骤三：如果电机的伺服驱动器中的驱动电流小于步骤二中的电流设定值时，那么此时的电机传动系统处于齿隙状态，进行步骤四。

步骤四：结合电机传动系统模型和能量最优控制原理，得到消隙器里的转换函数；驱动器向电机输入的电流经过消隙器里的转换函数，随着齿轮间隙角的增大快速增大，通过消隙器反馈给驱动器，使齿轮快速穿过齿隙。

进一步地，所述步骤一具体包括以下步骤：

s11:根据电机与负载之间的输入与输出关系，建立电机传动系统内部方程；

式(0)中cedn、θdn、idn、rdn、ldn、udn分别为第n台电机的反电动势系数、转角、电阻、电流、电感、电压。kdn、jdn、bdn、mdn、mxcn、i1分别为第n台电机的力矩系数、转动惯量系数、等效粘性摩擦系数、第n台电机轴的电磁转矩、与第n台电机轴所对应的第n个小齿轮的转矩、第n台电机与第n个小齿轮之间的传动比。jxcn、bxcn、mxcdcn分别为与第n台电机轴所对应的第n个小齿轮的转动惯量系数、等效粘性摩擦系数、第n个小齿轮和与之对应的第n个大齿轮之间的弹性力矩。θxcn、θdcn、i2、kxcdcn分别为第n个小齿轮的转角、第n个大齿轮的转角、第n个小齿轮和与之对应的第n个大齿轮之间的传动比、第n个小齿轮和与之对应的第n个大齿轮之间的传动刚度。jdcn、bdcn、mdcn、mf分别为第n个大齿轮的转动惯量系数、等效粘性摩擦系数、第n个大齿轮的转动力矩、末端负载的转矩。

jf、bf、kf、θf、tf分别为末端负载的转动惯量系数、等效粘性摩擦系数、传动刚度、末端负载的转角、末端负载与大齿轮之间的弹性力矩。

s12:由于受齿轮间隙非线性的影响，大小齿轮间隙函数为死区函数，具体表达式为：

上式中，θxcn、θdcn、i2、kxcdcn分别为第n个小齿轮的转角、第n个大齿轮的转角、第n个小齿轮和与之对应的大齿轮之间的传动比、第n个小齿轮和与之对应的大齿轮之间的传动刚度；(θxcn-i2θdcn)为大小齿轮间的位置差。

s13:建立电机端电压与齿轮间隙的关系；具体为：令α＝k3udn，其中k3为大齿轮与小齿轮之间的齿轮间隙系数，上面(1)式转换为：

定义齿轮间隙变量

θxcn-i2θdcn≥+k3udn

-k3udn<θxcn-i2θdcn<+k3udn

θxcn-i2θdcn≤-k3udn

得出大小齿轮间的齿隙表达式：对电机内部传动方程按照输入输出关系进行连接，得出含有齿隙的小齿轮和端电压的状态方程与含有齿隙的大齿轮和端电压的状态方程：

其中k1表示末端负载与大齿轮之间弹性力矩的力矩系数；

为了便于处理将上面的两个状态方程进行处理得出式(4)与(5)；即把小齿轮和端电压状态方程中的系数矩阵分成两行两列的方阵，得到小齿轮和端电压与大齿轮和端电压的关系，如下式：

(4)式与(5)式中，kdn、jdn、bdn、i1分别为第n台电机的力矩系数、转动惯量系数、等效粘性摩擦系数、第1台电机和与之对应的小齿轮间的传动比；jxcn、bxcn分别为与第n台电机轴所对应的第n个小齿轮的转动惯量系数、等效粘性摩擦系；θxcn、i2、kxcdcn分别为第n个小齿轮的转角、第2个小齿轮和与之对应大齿轮之间的传动比、第n个小齿轮和与之对应的大齿轮之间的传动刚度；jdcn、bdcn分别为第n个大齿轮的转动惯量系数、等效粘性摩擦系数；jf、bf、θf分别为末端负载的转动惯量系数、等效粘性摩擦系数、末端负载的转角；k1表示末端负载与大齿轮之间弹性力矩的力矩系数，k3为大齿轮与小齿轮之间的齿轮间隙系数。

进一步地，步骤二具体包括以下步骤：

s21:为了使控制系统在最短的时间内完成要求，采用最优控制的时间性能指标；时间性能指标公式为：

(6)式中j表示时间性能指标；xt2表示t2时刻的状态；根据控制系统应该满足的位置值、速度值，求解状态方程得出最优的时间性能指标；

s22:求解小齿轮穿越齿隙所需要的时间性能指标：

其中含有小齿轮的微分方程为：

(7)式中c1、c2为微分参数，小齿轮换向时的角速度：

(8)式中

当电机轴正传时：

当电机轴反转时：

取tf-t0作为小齿轮换向过程中，为克服齿轮间隙的时间性能指标，记为

s23:求解大齿轮穿越齿隙所需要的时间性能指标：

含有大齿轮的微分方程：

其中c3、c4为微分参数，大齿轮换向时的角速度：

式(11)中：

当小齿轮正传时：

当小齿轮反转时：

其中表示小齿轮开始转动与小齿轮带动大齿轮转动时，t0时刻所对应的的角速度值；

表示小齿轮开始转动与小齿轮带动大齿轮转动时，tf时刻所对应的的角速度值；

取t'f-t'0作为大齿轮换向过程中，克服齿轮间隙的时间性能指标，记为

s24:求得消隙器里的电流设定值：

因为电机小齿轮自身转角与大齿轮、大齿轮自身转角与负载是一体联动的，所以取两部分消耗的最短时间作为传动系统克服齿轮间隙的时间性能指标即：w为神经网络权重，ε为估计误差，用神经网络逼近最优控制的时间指标：由式(13)得消隙控制器的电流设定值：预设误差存在允许的误差范围、控制量udn以及对应的isn的误差范围，取误差范围的头尾值is1、is2作为消隙器的电流设定值。

进一步地，步骤四具体包括：

s41:为使控制系统消耗能量最少，需满足能量性能指标：

为了使能量性能指标最小，用最小值原理并结合控制系统的状态方程来构造哈密顿函；

哈密顿函数的一般表达式由状态过程量和控制系统的状态方程所组成，如式(16)：

由极小值原理知，当h(x，u，λ)最小时，性能指标j达最小；同时使h(x，u，λ)min成立的条件是h(x，u，λ)中的λbu达最小；式(16)中a、b为中的固定系数矩阵，所以使h(x，u，λ)min，必须使λ与u取到最小且λ与u符号要相反；对哈密顿求偏导数，得协态方程即状态方程中控制律u的符号为-sgn{λ·b}＝-sgn{e^-at·b}；因为λ与u符号相反，所以λu为负数，h(x，u，λ)min取得到，能量性能指标jmin取得到；

根据与极小值原理等价的古典变分法知：当时，哈密顿函数h(x，u，λ)取最小值，能量性能指标j也取最小值；因为公式(16)，所以当时，h(x，u，λ)取最小，状态方程中控制律u的数值为

s42：由小齿轮和端电压即式(4)与大齿轮和端电压即式(5)的关系得到齿轮间隙状态方程：

将齿隙状态方程即式(17)中的系数矩阵带入一般控制律u得齿隙控制律udn的符号与数值：

式(18)中λ1与λ2的取值决定能量最优控制律udn的符号，而式(18)与式(19)共同决定能量最优控制律udn的数值大小；

然后求解大小齿轮的齿隙微分方程：

其中c5、c6为微分参数，大小齿轮间的齿隙角度：

式(21)中

当电机正传或反转时，传动齿轮的齿隙表达式为：在双电机传动系统中，消除齿轮间隙的转换函数设置为：

s43：根据能量最优理论优化齿轮间隙的电流驱动曲线：

通过齿隙表达式(23)，可以得到双电机驱动电流表达式：

进一步地，还包括速度控制器；所述速度控制器用调节未知扰动引起的速度偏差，保证系统稳定性；具体包括以下步骤：

s51：设计基于变结构理论的速度积分滑模面；

设定位置控制器输出值即给定的电机速度与电机的反馈速度分别为w^*、w，则电机的实际速度偏差△为w^*-w，设计滑模面：

滑模面含误差的积分项和指数项，它们能在一定的时间内使误差快速收敛，保证系统稳定性；

s52：对式(26)求导，得出改进一般的滑模趋近律：

当一般控制系统从滑模面运动到终末状态，即时，此时s＝0，系统恢复稳定，

当一般控制系统从滑模面运动到终末状态，即时，此时s＝q，系统才稳定，

一种基于最优控制的双电机消隙系统，包括速度控制器、消隙器、pid位置控制器、控制n台电机的减速机相连的n台伺服驱动器、n台装有编码器的伺服电机、n台每台分别连接一台伺服电机的减速机以及负载；各电机与减速机的速度传输至速度控制器，速度控制器将传速度偏差值传输至各个电机对驱动电流进行判断，如果驱动电流小于设定值，则进行步骤四，消隙控制器向驱动器输入电流，实现动态的增大驱动电流，使齿隙快速缩短；位置控制器是用来调整给定位置与负载末端实际位置之间的位置偏差。

双电机传动系统的控制结构如图1所示；机械结构如图2所示；消隙控制器中的新型转换函数如图3所示；传动系统在运行时，施加给电机的驱动力矩如图4所示。

本发明中从齿轮传动系统的运行机理入手，将电机内部的回路平衡方程、电磁转矩方程、大小齿轮间的动力学方程、大小齿轮间的弹性力矩方程、负载端动力学方程结合在一起，从表达式可得出小齿轮、大齿轮、负载分别与输入端间的关系，为齿隙消除问题做准备。

传统齿轮间的齿隙问题一般采用基于速度控制器的变值偏置力矩来解决，这是基于电流设定值的力矩补偿控制，电流设定值选取的合理与否决定了控制方法的实际效果。工程中通常将电机额定运行时的10％～30％电流值选取为电流设定值。当速度控制器输出的驱动电流值小于设定电流时，说明传动齿轮处于启动、停止、换向这三个状态，消隙器会对电流进行偏置处理，输出正向偏置的电机1的驱动电流和负向偏置的电机2的驱动电流；当驱动电流大于设定电流时，逐渐减小偏置电流的大小直至为零，最终向双电机直接输出由速度控制器生成的驱动电流，实现双电机的同步驱动。

正对上段的问题，本发明从齿轮传动系统中的运行机理入手，推导出传动系统的一般状态方程，根据最优控制中的时间最优控制理论和传动系统的一般状态方程，得出负载转角达到相应标准的最短时间，并用神经网络逼近时间性能指标，得出最短时间内传动系统的控制量的变化范围，从而确定电流的设定值。相比工程上的经验数值，该电流设定值更加精确。

采用变值偏置力矩来解决传统齿轮间的齿隙问题时，在启动、停止、换向这三个阶段对电机施加额定扭矩的10％～30％作为消隙驱动力矩，这是根据日常工作得出来的经验数值，并没有从齿轮传动系统中的运动机理去考虑间隙角度的变化情况，因此以等腰梯形为主的转换函数并不能完全反应齿轮间隙角度的变化情况，由于齿隙变化角并不是恒定减小和增大，它是一个变加速变化的齿轮间隙角，过大或过小的恒定补偿力矩都会使增大或减少间隙角补偿的应有值，从而加剧齿轮间的碰撞，容易使齿轮抖动，影响传动系统运行的稳定性。

针对上段的现状，本发明从齿轮传动系统中的运动机理入手，推导出传动系统的一般状态方程，并表示出齿轮间隙角的变化状态方程。根据齿轮间隙角的状态方程，运用最优控制中使能量最优控制达到最优的哈密顿函数并结合古典变分法，得出齿轮间隙角状态方程中的控制量电压变化值，以齿轮间隙角状态方程里的齿轮间隙角表达式作为转换函数，从而得出消隙驱动电流(力矩)表达式。该驱动电流表达式能够根据齿隙角的变化情况来调整电流补偿值，在一定程度上避免大小齿轮间的碰撞。

现有技术中，采用滑模变结构理论中的传统指数趋近律来设计的速度控制器，在接近滑动模态时，会产生严重的抖动现象。为了在一定程度上减弱抖振，且由于远离滑动模态阶段收敛速度过小而导致的趋近时间过长等问题，我们需要重新设计速度控制器的趋近律。

针对上段的问题，本发明从一般趋近率入手，对一般趋近律中的等速项和函数项进行优化。从方法上保证双电机传动系统在远离切换面时，能以较大的速度趋近滑模面，在有限的时间内趋近滑模面。在接近切换面时，能降低趋近速度，减少传动系统运行的抖振现象。

虽然本发明已以较佳实施例公开如上，但它们并不是用来限定本发明的，任何熟习此技艺者，在不脱离本发明之精神和范围内，自当可作各种变化或润饰，因此本发明的保护范围应当以本申请的权利要求保护范围所界定的为准。