一种配电网无功优化方法与流程

本发明涉及供电
技术领域：
，尤其涉及一种配电网无功优化方法。
背景技术：
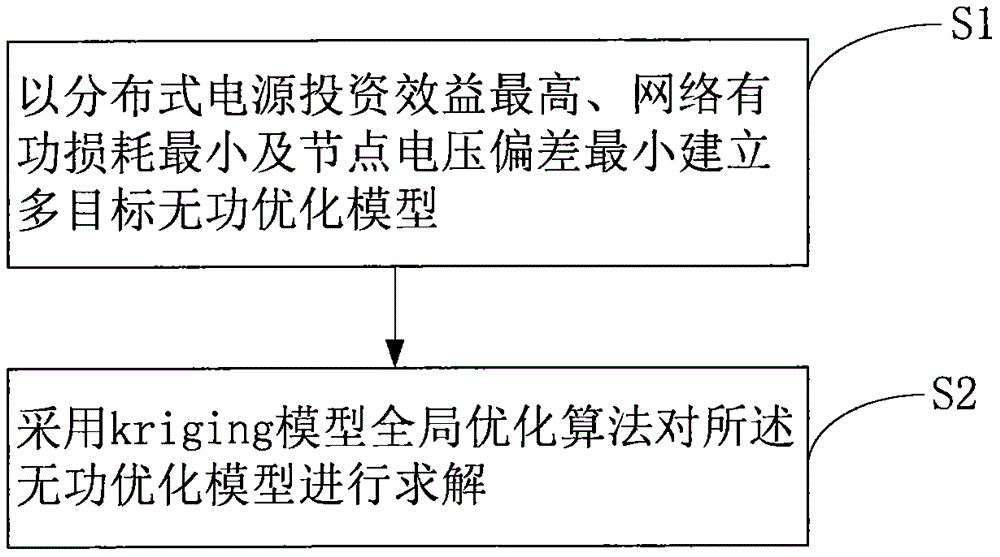
：大规模分布式电源(dg)并网，使配电网结构变复杂。而配电网无功功率平衡对保障电能质量至关重要。大规模分布式电源并网势必改变配电网的潮流分布，使电网中的无功潮流改变，若某个节点无功不足或过剩，则会降低电压质量。通过逆变器并网的dg，如直驱式风电机组和光伏系统等，可以对并网功率实现有功功率和无功功率独立调节。使含dg的配电网无功优化控制既要解决静止无功补偿装置(svc)的无功出力，又要处理dg的无功出力，同时还要考虑投切电容器组挡位、有载调压器分接头位置这些离散变量。在实际运行中，dg和大部分负荷都具有较强的随机性，又有储能装置及电动汽车等可控负荷，对优化目标也有新的要求，以满足电网运行的安全性和经济性。技术实现要素：基于此，有必要针对上述问题，提供一种含dg配电网的配电网无功优化方法，实现多目标配电网无功优化。一种配电网无功优化方法，包括以下步骤：s1，以分布式电源投资效益最高、网络有功损耗最小及节点电压偏差最小建立多目标无功优化模型；以及s2，采用kriging模型全局优化算法对所述无功优化模型进行求解。利用本发明提供的配电网无功优化方法可以对含dg配电网的配电网进行无功优化，实现多目标配电网无功优化。附图说明图1为本发明实施例提供的配电网无功优化方法流程示意图。图2为本发明实施例提供的基于kriging元模型全局优化算法求解无功优化问题的流程图。图3为本发明实施例中改造后的节点测试系统示意图。具体实施方式为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。请参见图1，本发明实施例提供一种配电网无功优化方法，包括以下步骤：s1，以分布式电源投资效益最高、网络有功损耗最小及节点电压偏差最小建立多目标无功优化模型；s2，采用kriging模型全局优化算法对所述无功优化模型进行求解。步骤s1中，建立所述含分布式电源的配电网无功优化模型需要考虑源荷不确定性及电容器组等动作次数约束，本申请中利用概率场景生成和场景削减的方法描述源荷不确定性。风力发电机的有功输出和风速有关，风速一般服从威布尔分布，概率密度函数为：其中，v是风速，k、c分别为威布尔分布的形状、尺度参数，k、c由风速24小时观测均值和方差计算得出，则风电发电机组有功功率输出为：其中，pr为额定风功率出力，vr、vci、vco分别为额定、切入和切出风速。太阳光照强度beta分布模拟，基于此得出太阳能光伏电池方阵输出功率的概率密度函数为：其中，α和β是beta分布的形状参数，由光照的平均值和方差计算，pm为方阵输出功率，rm为方阵最大输出功率且与方阵总面积和光电转换效率成正比。负荷功率概率分布采用正态分布进行模拟，表达式为：其中，μp、μq和σp、σq分别为有功负荷和无功负荷的期望和方差。储能装置(ess)模型，本申请考虑电化学储能，设电池在控制周期内的充放电过程以恒功率进行，设单个ess在t时段的荷电状态为s，其中，pba(t)为电池注入功率，其值为正表示电池放电，其值为负表示电池充电，其值为零表示既不充电也不放电，为充放电效率，δt为控制时间间隔，swh为ess额定容量。由于分布式电源和负荷均具有随机性，储能装置作为可控负荷和电源，对削谷填峰改善电压有积极作用。对于随机性源荷，本申请对每个随机变量的累积概率分布曲线的纵轴等概率分成n个空间，有p个随机变量，则通过采样后得到一个n×p的采样矩阵，通过迭代计算，最后形成n个采样场景，场景集合为sc。为满足抽样规模，n取值大，精度高，但降低了计算效率，因此可采用同步回代削减sbr技术进行场景削减，通过计算场景间的概率距离，找到与其距离最短的场景，合并相似的场景并确定相应概率。基于源荷不确定性，选取分布式电源、无功补偿装置和储能放电时的无功出力为连续控制变量，电容器组无功投切容量、有载调压器(oltc)分接头位置为离散控制变量；以dg投资效益最高、网络有功损耗最小及节点电压偏差最小建立多目标无功优化模型。即：分布式电源投资效益b：其中，b为dg投资效益，b1为dg年投资收益，b2为dg年投资成本。配电网有功损耗ploss：其中，为系统在场景sc下第t时段的有功网损；sc为总的场景数，psc为第sc个场景发生的概率，n1为配电网支路数，m和n是支路的首末端节点的编号；vm，sc，t、vn，sc，t分别为节点m和n在场景sc下第t时段的电压幅值；gk(m，n)为节点m和n之间支路的导纳元素的实部；θm，n，sc，t为节点m和n之间在场景sc下第t时段的电压相角差。节点电压偏差dv其中，nl为配电节点数，sc为场景集合的个数；为第sc个场景下，t时段，m节点电压的给定值，一般设为1.0pu；和分别是第sc个场景下，t时段，节点m处的最大电压限值和最小电压限值。对目标进行归一化处理，其中，α1、α2和α3分别是分布式电源年投资效益、系统有功网损、节点电压偏差的归一值。bmax和ploss，min分别是单独以分布式电源效益、有功网损为单一优化目标时得到的投资效益最大值和有功网损最小值。bmin和ploss，max是不进行优化时得到的分布式电源效益和有功网损值。采用权重系数法，将问题进行转化求解，建立满意度函数：f＝aα1+bα2+c(1-α3)(13)a、b、c为权重系数，采用以有功损耗为主的层次分析法，a、b、c分别取值为：0.1，0.7，0.2，f为满意度值，其值越接近1，说明优化方案越理想。约束条件动态无功优化的约束条件包括等式约束条件和不等式约束条件。其中等式约束条件即为潮流约束等式方程：其中，n为配电网中的节点总数；pgm、qgm为分布式电源在节点m处输出的有功功率和无功功率；pdm、qdm为在节点m处的负荷的有功功率和无功功率。电容器组无功补偿容量(组数)有载调压变压器分接头位置svc无功功率满足的不等式约束及考虑电容器组投切次数和有载调压变压器分接头动作次数约束：其中，nc、nt、nsvc、ness分别为并联电容器组、oltc、svc、ess个数，和分别为第m个并联电容器组允许最大组数和最小组数，分别是第k个oltc分接头位置调节上下限，为第m个svc允许的最大、最小无功功率输出，为第m个ess放电时，允许的最大、最小无功功率输出，mm为第m个电容器组日限制动作次数，zk为第k个oltc日限制动作次数。dg、ess运行约束应满足：其中，分别是m个dg在场景sc下第t时段的有功出力和有功出力的预测值；为第m个dg在场景sc下第t时段的无功出力和无功出力的上限值，ndg为dg个数；sess(t)为储能容量，sess，max、sess，min为储能容量上下限；为第m个ess在放电状态下，场景sc下第t时段的无功出力和无功出力的上限值，ness为ess个数。dg和放电状态下的ess能提供的无功功率最大值满足：其中，s为并网逆变器能提供的最大视在功率。节点电压约束为：和分别是第sc个场景下，t时段，节点m处的最大电压限值和最小电压限值。步骤s2中，采用kriging模型全局优化算法对无功优化进行求解，具体的求解过程如下：多阶段求解方法由于约束条件中考虑离散变量投切次数，并考虑了求解时段的划分，使得所建立模型的求解是具有时空耦合性的非线性整数规划问题，难以直接求解。因此根据被控量的调节特点将其划分为基础调节量和补充调节量。在此基础上，无功优化模型的求解分三个阶段：第一阶段，以电容器组数、有载调压器(oltc)分接头位置、dg、svc及放电状态下ess的无功出力为控制变量，不考虑前二者的动作次数限制，以每个小时满意度为目标，计算24小时内每小时每个控制量取值。第二阶段，只考虑电容器组数和oltc分接头位置作为基础调节量，连续变量保持不变，以24小时满意度为目标函数，同时考虑离散变量动作次数约束和节点电压约束，计算得出每个小时的电容组投切容量和oltc位置。第三阶段，dg、svc、ess无功出力作为补充调节量再调整，离散变量保持不变，以每个小时的满意度为目标，固定第二步离散变量值，计算得出每小时dg、svc无功出力，并根据ess状态确定其无功出力。通过三个阶段，得到以满意度最接近于1为目标的每小时内控制变量的值。基于kriging模型全局优化算法求解含dg配电网多目标无功优化多阶段求解方法中，每一阶段都是对某个配电网无功优化模型的求解。本申请提出基于kriging元模型的全局优化算法并用于求解配电网多目标无功优化问题。假设kriging元模型的目标函数为y(x)，根据已知的观测点的自变量和响应值，kriging模型的回归方程为：其中，f(x)为回归模型的基函数，β为对应的系数，z(x)为一组随机变量过程，且满足随机变量的期望为零。初始设计区域、目标函数和约束条件、设计变量为已知，在初始设计区域中进行采样，应用目标函数及约束条件对试验点进行评估，将实验区域进行分割，在分割后的区域中再进行采样和kriging模型拟合，进行局部优化，直到设计区域都被访问，并满足终止判据为止。图2为基于kriging元模型全局优化算法求解无功优化问题的流程图。算例介绍及仿真分析本申请中配电网无功优化方法的数值模拟和仿真计算由matlab完成，配电网运行模拟和潮流计算由opendss完成，基于kriging元模型的全局优化算法在matlab上实现，并调用opendss来进行目标函数和约束条件计算。以改造后的ieee33节点配电系统为例。改造后的节点测试系统如图3所示。参数如下：保持线路参数不变，oltc电压比范围为0.9～1.1pu，上下共16挡位，步进量为0.625％；ess为储能装置，放电功率上限为0.24mw，荷电状态为30％～90％，充电效率为80％，放电时具有无功调节能力。dg1、dg2为直驱式风电机组，dg3为光伏系统，svc1和svc2的补偿容量取-600kvar～600kvar；c1和c2为两台并联补偿电容器，每台7组，每组补偿容量为100kvar；oltc、电容器的日最大调节次数均设置7次，单次动作成本为6元。各节点电压取值范围0.95～1.05pu；系统三相功率基准值sb＝10mva，线电压基准值为ub＝12.66kv；结合场景削减算法，在24h内得出10个削减后的场景，分别为sc1，sc2…sc10，并得出每个场景的概率，psc1，psc2…psc10。如表1所示。因篇幅限制，本申请列出t＝14h风电、光伏、储能、负荷各场景情况。表1削减后各场景概率psc1psc2psc3psc4psc5psc6psc7psc8psc9psc100.00860.11330.15330.06670.05330.18670.11330.10670.07330.08表2t＝14h风力出力场景场景sc1sc2sc3sc4sc5sc6sc7sc8sc9sc10功率(kw)437347309315167366186276450225表3t＝14h光伏出力场景场景sc1sc2sc3sc4sc5sc6sc7sc8sc9sc10功率(kw)456162235287500437363338365434表4t＝14h负荷场景场景sc1sc2sc3sc4sc5sc6sc7sc8sc9sc10功率(kw)800523660615669648621599611592以t＝14h为例，对是否考虑源荷不确定性及动作次数约束的无功优化结果进行分析，校验结果如下表。表5t＝14h各情况的最优无功计划考虑源荷不确定性和动作系数限制的无功模型与既不考虑源荷不确定性又不考虑动作次数限的无功模型都有较高的满意度，但考虑源荷不确定性和动作系数限制的无功模型更符合实际运行的情况，具有更好的适应性。为测试本申请提出的基于kriging元模型全局优化算法的有效性，将其与已有文献中的粒子群算法(pso)对比。粒子群算法初始参数为：初始种群设为20，最大、最小惯性权重分别为0.9，0.6，学习因子均取2.0。两种算法无功优化结果对比，以t＝5h为例。表6t＝5h优化结果及算法性能对比通过对比分析，应用本申请提出的基于kriging模型的全局优化算法在满意度、平均迭代次数、平均评价次数及平均计算时间上都优于粒子群算法，有效提高了寻优速度和求解效率，并有较好的全局收敛性。利用本发明提供的配电网无功优化方法可以对含dg配电网的配电网进行无功优化，实现多目标配电网无功优化。以上所述实施例仅表达了本发明的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对本发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。因此，本发明专利的保护范围应以所附权利要求为准。当前第1页12