一种适用于配电网分布式电压控制的新型分区方法与流程

本发明涉及分布式电源配电
技术领域：
，具体涉及一种适用于配电网分布式电压控制的新型分区方法。
背景技术：
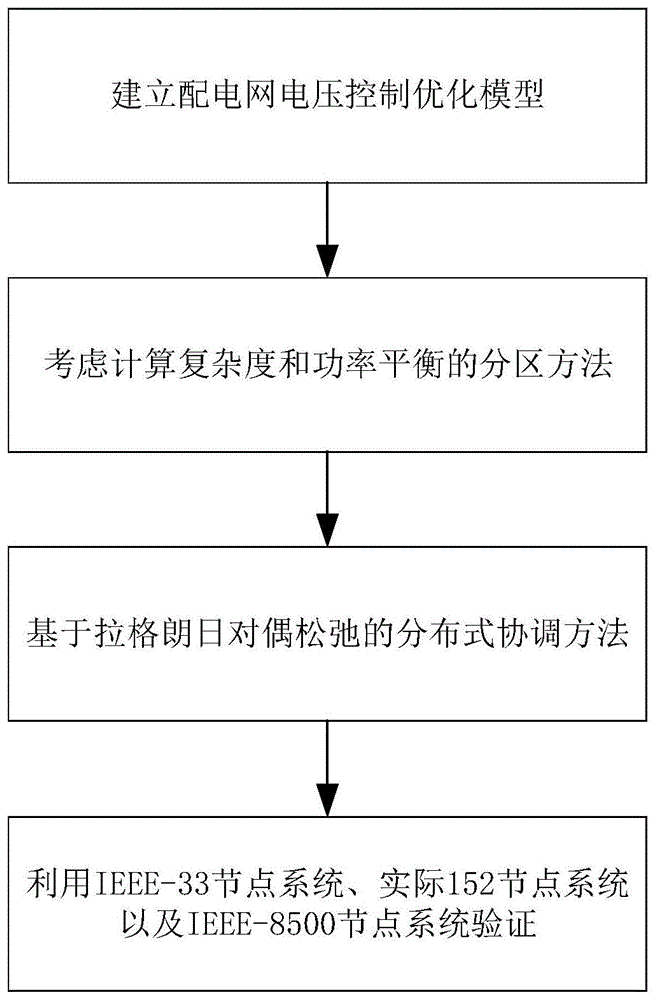
：近年来，随着风力发电(windturbinegeneration，wtg)和光伏发电(photovoltaicgeneration，pvg)等分布式电源的不断发展，主动配电网的结构变得越来越复杂。分布式电源(distributedgenerations，dgs)的高渗透性会对电压产生较大的负面影响，如何有效协调dgs对电压进行控制成为主动配电网要解决的一个重要问题。此外，集中式优化方法在电压控制中的应用比较广泛，但是在大规模实际配电网的计算中经常遇到较大的瓶颈。因此，分布式电压控制成为了主动配电网中的一个很有前途的研究方向。为了实现有效的分布式控制，合理的网络划分方法也对实现电压的分布式控制具有重要意义。一直以来，有载调压变压器(onloadtapchanger,oltc)、电容器组(capacitorbanks,cbs)调整和静态无功补偿器(staticvarcompensator,svc)被视为防止电压越限的有效控制措施，而dgs只在固定功率因数下运行用来提供电压支持。然而，如果这些机械设备被频繁操作以防止dgs的间歇性输出造成的电压越限，它们的寿命将大大缩短。因此，配网中可以将分布式电源用在缓解频繁电压越限方面，并作为主动配电网中电压控制的一个特殊措施。有学者定义了四个运行点来描述dgs的电流极限，利用这些点所连接的多边形来逼近dgs的容量曲线。另为了应对光伏发电机组冲击造成的电压调节损失，turitsyn等人比较了控制系统管理光伏逆变器产生的无功功率的不同设计方案来得到最优方案。然而，在之前的研究中没有考虑pvg和wtg的有功和无功功率的耦合限制，提出的四个运行点也很难预先设定。在实际应用中，配电网可以通过吸收dgs的无功功率来减小电压波动。因此，需要建立一个更为精细的dgs容量曲线模型来进行电压控制减少电压波动。此外，储能系统(energystoragesystems,esss)可以通过改变主动配电网的功率分布，来进行有效的电压控制。因此，考虑dgs的精细容量曲线的影响以及主动配电网中esss的调节，对制定一种有效的电压控制策略具有重要意义。此外，dgs和其他大规模的主动控制设备接入实际配电网中，给传统的集中式电压控制带来了巨大的技术挑战(比如计算负担等)。多时段的电压集中控制模型实际上是一个大规模的时空耦合调度问题，会带来计算量巨大的挑战。而且，集中式算法不适合主动配电网未来发展所需的即插即用功能。分布式控制方法能够有效地解决传统集中式电压控制方案的不足，有利于dgs与其他可控器件的有效协调。合理的网络划分是主动配电网分布式电压控制的前提，网络划分方法将整个电网划分为若干个子区域，其特点是内部节点之间关系强，而不同子区域的节点之间关系弱。现有的划分方法包括k-均值方法、谱聚类方法、免疫算法、复杂网络理论等。但是由于划分的子问题中最长的优化时间决定了整个模型的计算效率。因此，为了提高计算效率，还应考虑计算复杂度。需要根据优化模型中决策变量的个数和约束条件的个数，从优化过程中乘法运算和加法运算的次数来分析计算复杂度。因此，需要一种新型的考虑计算复杂度和功率平衡的网络划分方法，以求得主动配电网中分布式电压控制的最优划分。在以往的研究中，包括交替方向乘子法(alternatingdirectionmultipliermethod,admm)、辅助问题原理(auxiliaryproblemprinciple,app)和拉格朗日对偶松弛法的许多算法，被应用于协调相邻区域。wang等人开发了一种基于一致性的admm方法，以分布式方式解决多区域协调网络约束机组组合问题。但是，admm算法的计算效率与惩罚因子的选择密切相关，app算法的收敛速度对辅助函数参数的选择也很敏感。而拉格朗日对偶松弛法能够克服这些缺陷，利用拉格朗日对偶松弛法不需要选择罚因子或辅助函数参数。综上所述，基于新型分区方法的配电网分布式电压优化控制模型是配电网运行优化研究中的一个重要的技术。技术实现要素：本发明目的在于提供一种适用于配电网分布式电压控制的新型分区方法，得到配电网合理的网络划分结果，并且利用不同区域的联络线上的协调方法，使得配电网中在同一联络线上的不同区域间的可以快速协调，提高配网电压优化控制的效率并降低网损；本发明所采用的技术方案是：一种适用于配电网分布式电压控制的新型分区方法，包括下面步骤：步骤1：通过二阶锥松弛的潮流约束，建立以待研究配电网区域总网损最小和节点电压幅值偏差最小为目标的主动配电网的电压控制模型，执行步骤2；步骤2：通过建立电气距离的模块化函数，建立一个网络分区方法用以主动配电网分布式的控制，通过网络分区方法将配电网区域总网系统划分多个子区域，其中，每个划分后的子区域中的决策变量和约束的数量来量化计算复杂度函数，执行步骤3,；步骤3：结合相邻的两个子区域之间的分区方法，在边界总线中向边界的每个子区域添加一个辅助发电源，建立分布式协调模型，执行步骤4；步骤4：基于拉格朗日对偶松弛的分布式求解方法对分布式协调模型进行求解，根据边界子区域之间的局部信息交换，对边界变量进行协调和更新得到待研究配电网的最优决策结果，通过最优决策结果来限定光伏机组和风电机组功率的出力，结束。优选的，所述步骤1中，对待研究配电网分别建立光伏机组和风电机组的容量曲线，通过容量曲线和定转子容量来限定光伏机组和风电机组的可行子区域。优选的，所述步骤1中，主动配电网的电压控制模型的建立过程为：步骤31：电压控制模型的目标函数为最小化网络损耗和母线电压的偏差，目标函数为其中，ij表示从节点i到节点j的正潮流方向，e是线路集合，b是节点集合，rij表示支路ij的电阻，iij，t表示支路ij在t时间段内的电流，vi，t表示节点i处的电压值，和分别表示支路电流的平方和节点电压的平方，xij表示ij支路的电抗，gj和bj分别表示节点j对地的电导和电纳；pj，t和qj，t分别表示t时间段内节点j处的有功和无功功率注入；步骤32：通过二阶锥松弛技术，得到表达式为和分别表示t时段内从节点j的风电、光伏和变电站注入的有功功率；分别表示t时间段内从节点j处的变电站注入的无功功率；t时段节点j并联电容器组、风电、光伏发电的无功功率分别用来表示；和表示t时段节点j的有功负荷和无功负荷；pij，t和qij，t表示t时段支路ij的有功和无功潮流，执行步骤33；步骤33：当一次侧的电压固定时，变压器为电压控制模型的一个节点，得到风电机组的有功和无功功率的输出界限由其定子电流和转子电流决定，风电机组出力的可行子区域为光伏机组的有功和无功出力的可行子区域为其中，为风电机组视在功率上限，用γ表示最大功率因数，预测的有功功率为光伏机组的视在功率上限。7.优选的，所述步骤3中，网络分区方法的具体内容包括下列步骤：步骤41：将总网络系统分解成np各不重叠的子区域，子区域之间的连接线路为ij，在每个子区域的边界节点i和j出各添加一个辅助发电机，辅助发电机的功率输出为pij和qij，边界节点的功率平衡约束条件为其中，etie-line表示连接边界节点i和j的支路，执行步骤42；步骤42：计算相邻两个节点之间的电气距离，网络节点中i和节点j之间的电气距离为其中，所述电气距离定义为测量两个节点之间关系的紧密性，执行步骤43；步骤43：将两个子区域进行合并得到一个新的子区域，计算综合指数，并采用综合指数最大的组合结果，当综合指标值达到最大值时，组合操作停止，从而得到最优分区数。优选的，所述步骤2中，所述复杂度函数的计算过程为，其中ωm和ωn分别是tm和tn的权重，ωm＝1，ωn＝0，tm表示复杂度函数模型中的乘法运算次数，tn表示复杂度函数模型中的加减法运算次数。优选的，所述步骤2中，所述网络分区方法的工作过程为：步骤61：每一个独立的子区域即为一个节点，计算子区域的综合指标执行步骤62；步骤62：选取一个子区域定义为一个a区域，在除a区域以外的其他区域中随机选取一个子区域定义为b区域，a区域和b区域组合形成一个新的子区域，并计算新的子区域的综合标的变化在计算中，采用最大正值为的合并结果作为更新后的综合指数步骤63：将所述步骤63中的新的子区域作为单独的节点，重复步骤62；直至没有节点可以合并时，执行步骤64；步骤64：综合索引达到最大值时，分区过程停止，当前的分区方案就是是最佳的分区结果。与现有技术相比，本发明的有益效果是：(1)分别建立光伏机组和风电机组的容量曲线，利用容量曲线和定转子容量来限制光伏机组和风电机组功率的可行域，考虑其在配网运行优化中的作用；(2)利用基于电气距离的模块化函数，引入一种考虑计算复杂度和功率平衡的新型网络划分方法，其中使用每个区域(利益主体)的决策变量和约束的数量来量化计算复杂度，作为配电网分布式优化运行的前提。(3)引入两个相邻利益主体之间的协调方法，在边界总线中向边界的每个主体添加一个辅助发电源，以便更好的求解分布式协调模型；(4)提出了一种基于拉格朗日对偶松弛的分布式求解方法，该方法不需要任何中心协调，只需要边界利益相关者之间的局部信息交换，对边界变量进行快速协调和更新，得到最优决策结果。附图说明图1是配电网分区分布式电压控制优化流程图；图2是风电机组的容量曲线；图3是光伏机组的容量曲线；图4是两个相邻子区域支路的分解；图5是各子区域辅助发电机示意图；图6是ieee-33节点系统的网络划分结果；图7是ieee-33节点系统的分布式算法对偶间隙；图8是有无容量曲线的电压偏差结果比较；图9是有无ess的电压偏差结果比较；图10是有无ess的电压平方的影响比较；图11是实际的152节点系统的拓扑结构；图12是实际的152节点系统的分布式算法对偶间隙；图13是ieee-8500节点系统的拓扑结构；图14是ieee-8500节点系统中分布式算法的对偶间隙。具体实施方式下面结合本发明的附图1～14，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施。在本发明的描述中，需要理解的是，术语“逆时针”、“顺时针”“纵向”、“横向”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”、“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。实施例1：一种适用于配电网分布式电压控制的新型分区方法，包括下面步骤：步骤1：通过二阶锥松弛的潮流约束，建立以待研究配电网区域总网损最小和节点电压幅值偏差最小为目标的主动配电网的电压控制模型，执行步骤2；步骤2：通过建立电气距离的模块化函数，建立一个网络分区方法用以主动配电网分布式的控制，通过网络分区方法将配电网区域总网系统划分多个子区域，其中，每个划分后的子区域中的决策变量和约束的数量来量化计算复杂度函数，执行步骤3,；步骤3：结合相邻的两个子区域之间的分区方法，在边界总线中向边界的每个子区域添加一个辅助发电源，建立分布式协调模型，执行步骤4；步骤4：基于拉格朗日对偶松弛的分布式求解方法对分布式协调模型进行求解，根据边界子区域之间的局部信息交换，对边界变量进行协调和更新得到待研究配电网的最优决策结果，通过最优决策结果来限定光伏机组和风电机组功率的出力，结束。值得说明的是，所述步骤1中，对待研究配电网分别建立光伏机组和风电机组的容量曲线，通过容量曲线和定转子容量来限定光伏机组和风电机组的可行子区域。值得说明的是，所述步骤1中，主动配电网的电压控制模型的建立过程为：步骤31：电压控制模型的目标函数为最小化网络损耗和母线电压的偏差，目标函数为其中，ij表示从节点i到节点j的正潮流方向，e是线路集合，b是节点集合，rij表示支路ij的电阻，iij，t表示支路ij在t时间段内的电流，vi，t表示节点i处的电压值，和分别表示支路电流的平方和节点电压的平方，xij表示ij支路的电抗，gj和bj分别表示节点j对地的电导和电纳；pj，t和qj，t分别表示t时间段内节点j处的有功和无功功率注入；步骤32：通过二阶锥松弛技术，得到表达式为和分别表示t时段内从节点j的风电、光伏和变电站注入的有功功率；分别表示t时间段内从节点j处的变电站注入的无功功率；t时段节点j并联电容器组、风电、光伏发电的无功功率分别用来表示；和表示t时段节点j的有功负荷和无功负荷；pij，t和qij，t表示t时段支路ij的有功和无功潮流，执行步骤33；步骤33：当一次侧的电压固定时，变压器为电压控制模型的一个节点，得到风电机组的有功和无功功率的输出界限由其定子电流和转子电流决定，风电机组出力的可行子区域为光伏机组的有功和无功出力的可行子区域为其中，为风电机组视在功率上限，用γ表示最大功率因数，预测的有功功率为光伏机组的视在功率上限。优选的，所述步骤3中，网络分区方法的具体内容包括下列步骤：步骤41：将总网络系统分解成np各不重叠的子区域，子区域之间的连接线路为ij，在每个子区域的边界节点i和j出各添加一个辅助发电机，辅助发电机的功率输出为pij和qij，边界节点的功率平衡约束条件为其中，etie-line表示连接边界节点i和j的支路，执行步骤42；步骤42：计算相邻两个节点之间的电气距离，网络节点中i和节点j之间的电气距离为其中，所述电气距离定义为测量两个节点之间关系的紧密性，执行步骤43；步骤43：将两个子区域进行合并得到一个新的子区域，计算综合指数，并采用综合指数最大的组合结果，当综合指标值达到最大值时，组合操作停止，从而得到最优分区数。优选的，所述步骤2中，所述复杂度函数的计算过程为，其中ωm和ωn分别是tm和tn的权重，ωm＝1，ωn＝0，tm表示复杂度函数模型中的乘法运算次数，tn表示复杂度函数模型中的加减法运算次数。优选的，所述步骤2中，所述网络分区方法的工作过程为：步骤61：每一个独立的子区域即为一个节点，计算子区域的综合指标执行步骤62；步骤62：选取一个子区域定义为一个a区域，在除a区域以外的其他区域中随机选取一个子区域定义为b区域，a区域和b区域组合形成一个新的子区域，并计算新的子区域的综合标的变化在计算中，采用最大正值为的合并结果作为更新后的综合指数步骤63：将所述步骤63中的新的子区域作为单独的节点，重复步骤62；直至没有节点可以合并时，执行步骤64；步骤64：综合索引达到最大值时，分区过程停止，当前的分区方案就是是最佳的分区结果。实施例2：一种适用于配电网分布式电压控制的新型分区方法，主动配电网的电压控制模型，在本发明中，目标函数为最小化网络损耗和母线电压偏差，即：其中f是指模型的目标函数，t是总时间段，表示t时间段内的总网络损耗，ij表示从节点i到节点j的正潮流方向。e是线路集合，b是节点集合。rij表示支路ij的电阻，iij，t表示支路ij在t时间段内的电流，vi，t表示节点i处的电压值。上述潮流约束(2)通常用于支路潮流模型，在采用二阶锥松弛技术后，形成表达式(2d)，和分别表示支路电流的平方和节点电压的平方。其中，δ(j)为功率流出节点为j的节点集合，π(j)为功率流入节点为j的节点集合。xij表示ij支路的电抗，gj和bj分别表示节点j对地的电导和电纳。pj，t和qj，t分别表示t时间段内节点j处的有功和无功功率注入。和分别表示t时段内从节点j的风电、光伏和变电站注入的有功功率。分别表示t时间段内从节点j处的变电站注入的无功功率。t时段节点j并联电容器组、风电、光伏发电的无功功率分别用来表示。和表示t时段节点j的有功负荷和无功负荷。pij，t和qij，t表示t时段支路ij的有功和无功潮流。式中，和是支路ij的电流平方下限和上限。和是节点j处的电压平方下限和上限。pij，t和表示支路ij的有功功率下限和上限。qij，t和表示ij支路的无功功率上下限。假设一次侧的电压是固定的，变压器可以建模为一个节点。因此，可以调整具有oltc的二次侧的电压。其中boltc是装有oltc的节点集合，是一个常量值。是一个离散变量，它表示oltc的可调比率平方，也就是电网侧电压与变电站侧电压的比率平方，可以表示为：其中，srj是在节点j处oltc可调节的最大挡位，和是0-1变量。在式(5b)中，用oltc调节比率变化的平方来表示离散的挡位。式(5c)中的第一个不等式用来保证调节的总数不超过而调节挡位的范围由式(5c)的其他不等式确定。式(5d)表示变电站功率注入的约束。在本发明中，假设每组cb的无功功率相同，则cb的约束条件和oltc的约束条件相似，即：其中bcb为并联电容器组的节点组，为离散变量，表示开关电容器组的个数，为每组的无功补偿。和是0-1变量，表示开关电容器组的状态。表示t时间段内开关次数的上限，而表示开关组数目的上限。wtg的实际有功出力不能超过预测的有功功率如式(7a)所示：wtg的有功和无功功率的输出界限由其定子电流和转子电流(视在功率上限)来决定。图1表示wtg出力的可行域。与wtg相似，pvg的有功和无功出力需要考虑到预测出力和转换器容量。此外，式(8c)还考虑了谐波损失，用γ表示最大功率因数，预测的有功功率视在功率上限图2表示pvg出力的可行域。其中，bess为储能系统所连接的节点组，和为0-1状态变量，分别表示充放电状态，和表示充放电上限，ej,t表示储能系统储存电量，和表示储能系统储能上下限，和表示充放电系数。值得说明的是，(2)分布式电压控制的网络分区方法在这一节，我们提出了一个新型的网络分区方法，除了电气距离还考虑了计算复杂度以及功率平衡，为后续主动配电网的分布式电压控制提供前提条件。1)两个相邻子区域之间支路的分解方法假设把一个网络系统分解成np各不重叠的子区域，如图3中的连接子区域1和2的联络线路ij，相关的变量也需要解耦。为了更加方便求解每个子区域的模型(即当地模型)，我们在每个子区域的边界节点i和j出各添加一个辅助发电机，如图4。如此，两个相邻子区域交换的功率pij和qij(省略时间指数t)就是辅助发电机的功率输出，则边界节点(以子区域1的节点i为例)的功率平衡约束条件便更新为(10a)和(10b)。其中，etie-line表示连接边界节点i和j的支路。接下来每个边界支路上的功率损耗都忽略不计，因为对于整个网络来说在联络线上的损耗是一个非常小的数量级。目前的研究中，边界变量的分解方法主要是支路撕裂法和节点解耦法。我们在此应用支路撕裂法是由于节点的特性不同。而且，不同区域之间联络线的网损太小不足以对整个电网的计算结果产生影响。zheng等人提出了一种分布式算法来解决主动配电网中多区域的经济运行问题，该方法即可证明忽略联络线上的网损不会对整个网络的计算结果产生较大的影响。以下两个等式可以保证任何子区域的交换功率与相邻子区域相等。2)电气距离利用电压灵敏度来反映网络中不同节点的dg注入功率的电压响应特性，为评估电气距离提供了依据。根据基于newton-raphson法的潮流计算修正方程，可以得到所有节点电压变化与注入功率之间的线性关系其中，δvpilot表示随δp和δq变化而产生的注入功率变化。by和gy分别是导纳矩阵的实部和虚部。因此，有功电压灵敏度jp和无功电压灵敏度jq可以表示为jp＝[(by+q)(gy-p)-1(by-q)+(gy+p)]-1(12a)jq＝-[(gy-p)(by+q)-1(gy+p)+(by-q)]-1(12b)通过利用电压灵敏度，可以将网络中节点i和节点j之间的电压变化的相互关系处理为因此，电气距离可以表示为：由于电气距离被定义为测量两个节点之间关系的紧密性，所以电气距离是对称的，。节点i和j或节点j和i之间的关系是相同的。在以前的研究中，分区的数目是预先指定的，但是这不足以得到分布式模型的最优结果。在这里，我们从开始认为所有的节点都是独立的，然后将这些子区域合并。根据式(15)，(16)，(21)和(22)，将任意两个子区域合并为一个新的子区域来计算综合指数，采用综合指标值最大的组合结果。当综合指标值达到最大值时，组合操作停止，从而得到最优分区数。分布式网络是以一个子区域为节点，在两个节点之间建立一个连接，按照模块化函数计算连接的权重：因此，模块化函数为：当节点i和节点j在同一子区域时，δ(i，j)＝1；否则，δ(i，j)＝0。3)功率平衡但是，在电网分区时，需要避免各分区dg机组数量不平衡的情况，也不能出现区域内发电量不足或过大的情况。因此，在网络划分时，我们需要功率平衡这个指标来判断dg在各个子区域的无功或有功功率平衡能力。假设网络被划分为np子区域，功率平衡可以表示为：其中，np是分区的个数和分别是a区域的有功和无功的需求。4)计算复杂度一般以所有子问题中最长的优化时间作为整个问题的计算时间，所以实际上，每个子问题的精确计算时间也会影响到整体计算效率。因此，在进行网络划分时，应考虑每个子区域的计算时间，而计算复杂度的函数可以根据约束和决策变量的数目来确定。也就是说，计算复杂度可以根据决策变量的数量和约束的数量来分析。为了清楚起见，我们使用以下形式的模型来获得计算复杂性的函数。s.t.δy∞＝snδu∞(17b)其中u∞表示与线性约束相关的输入变量。um表示与优化模型的二阶锥约束相关的输入变量。u表示所有输入变量。y∞是与线性约束相关的输出变量集，ym是优化模型中与二阶锥约束相关的输出变量集。δ表示这些变量的变化。式(17a)表示优化模型的目标函数(即式(1))。式(17b)是优化模型的等式约束(例如，式(2a)-(2c)和(2e)-(2f))。式(17c)和(17d)是关于决策变量(u和y)的不等式线性约束(例如式(3)-(4))。式(17e)和(17f)是关于决策变量(u和y)的二阶锥约束(例如式(2d)，(5d)，(7b)和(8b))。上述与线性约束相关的约束可以矩阵形式表示如下：由于上述线性方程的系数矩阵是一个三对角正定矩阵，采用高斯消去法对其进行处理。因此，与线性约束相关的乘法计算的次数如下tm(∞)＝5x∞-4(19a)与二阶锥约束相关的计算次数可以近似估计为与线性约束相关的计算次数的两倍。因此，整个优化模型的乘法运算次数可近似估计如下：tm＝10xm+5x∞-12(19b)与线性约束相关的加减运算次数为：tn(∞)＝3x∞-3(19c)因此，整个优化模型的加减运算次数可近似估计如下：tn＝6xm+3x∞-9(19d)其中，x∞表示与线性约束相关的输入变量矩阵δu∞的维数；xm表示与二阶锥约束相关的输入变量矩阵δum的维数；tm(∞)和tn(∞)分别表示与线性约束相关的乘法和加法运算次数；tm和tn分别表示整个优化模型的乘法和加法运算次数。综上所述，计算复杂度可以计算为：其中ωm和ωn分别是tm和tn的权重。在模拟程序中，进行乘法计算要比执行加法计算花费更多的时间。因此，这里我们只计算乘法的次数来估计简化的计算量。也就是说，ωm＝1和ωn＝0。5)综合指标由于模块化函数、功率平衡和计算复杂度在不同的数量级，如果不对它们规范化，网络划分方法的结果将受到最大数量级的影响。因此，这三个指标的范围应规范化为[0,1]，如下所示：在所有可能的分区结果中定义了(21a)和(21b)中的ρp和ρq最小值和最大值。当采用这种网络划分方法时，所有的节点在开始时都被视为独立的子区域，这些子区域可以合并。当综合指数达到最大值时，合并将停止。因此，式(21a)和(21b)不会对网络划分方法的计算方面产生影响。综合指数可以表示为：其中表示所有子区域中计算复杂性最大的数值。当达到最大值时，得到了最优分割结果。6)网络划分步骤网络划分的具体步骤如下：步骤1：将每一个节点设置为一个独立的子区域，计算综合指标步骤2：对于a区域来说，从其他区域中随机选择b区域，形成a区和b区组合的新的子区域(此步骤从所有区域开始，即此算法是并行的)。然后，计算每个合并结果的综合指数的变化在计算中采用最大正值为的合并结果。然后更新综合指数步骤3：将新形成的子区域作为单独的节点，重复步骤2以实现分区过程并获得新的分区结果。步骤4：当没有节点可以合并时，综合索引达到最大值时，分区过程停止，当前的分区方案就是是最佳的分区结果。(3)电压控制的分布式协调模型及求解算法在这一节中，我们应用基于拉格朗日对偶松弛的分布式算法来协调边界变量。应用变量分裂法后，模型(1)-(9)可转化为多个子问题，具体如下：s.t.ga(xa)≥0,a＝1,2,...,np(23b)ha1(xa)＝0,a＝1,2,...,np(23c)ha2(xa,xb∈a)＝0,a＝1,2,...,np(23d)ifij∈etie-line∩j∈ba∩i∈bb(23d)其中，fa(xa)是子区域a的目标函数；ga(xa)≥0是只与子区域a的内部参数相关的不等式约束；ha1(xa)＝0是只与子区域a的内部参数相关的等式约束；ha2(xa,xb∈a)＝0是子区域a与邻接子区域b的耦合关系的等式约束；etie-line表示边界节点为i和j的支路；xb∈a是区域b中的边界功率变量，但必须存在一条直接连接区域a和b的支路。将模型(25)视为原问题。基于拉格朗日对偶松弛理论，将压缩耦合约束松弛为目标函数，形成各子区域的拉格朗日函数，具体如下：其中，λa是ha2(xa,xb∈a)＝0的等式约束的松弛向量乘子。向量λa中的所有元素都是非负的。因此，通过最小化每个子区域的拉格朗日函数l(xa,λa)的最大值，模型(23a)可以等价于多个子问题。s.t.ga(xa)≥0(25b)ha1(xa)＝0(25c)λa≥0(25d)那么，模型(25)的目标函数可以表示为：在每一个对偶子问题中，内部变量xa是决策变量，也需要其他外部确定与两个边界子区域中的内部变量耦合的常数因此，当给定拉格朗日乘子λa时，子问题模型的内部模型可以具体表示如下：s.t.ga(xa)≥0(27b)ha1(xa)＝0(27c)根据模型(27)，并行计算每个子问题以获得每个子区域xa.的相应结果。然后，根据得到的变量值xa和用下一部分描述的次梯度算法更新每个区域的拉格朗日乘子λa。通过交换和协调边界变量可以得到全局优化结果。值得注意的是，在计算每个子区域a中的子问题时，只需要与子区域a相连的相邻子区域的边界信息，即不需要将子问题的结果发送到所有其他子区域。设模型(28)为对偶问题：式(26)的外部模型是最大化目标函数采用次梯度算法对拉格朗日乘子λa进行迭代更新。第n+1次迭代的表达式如下：其中为步长，sa(n)为第n次迭代中模型(26)的松弛约束ha2(xa,xb∈a)的次梯度方向，可表示为：其中c和d是正值常数。由于ha2(xa,xb∈a)＝0代表表达式(10c)，因此每个子区域只需要将联络线潮流信息发送到相邻子区域，即每个子区域中的调度不需要发送到所有其他子区域。我们也可以从式(29b)中找到这个特征。对于每次迭代中的一组解原问题和对偶问题的绝对对偶间隙g如下所示：根据对偶最优定理，如果g＝0，则是原对偶问题的最优解。值得说明的是，对改进的ieee-33节点和实际的152节点系统进行了算例分析，以证明所提出的模型的有效性。这些实验由cplex12.6.0利用matlabr2016a在一台具有intel内核(i5，3.20ghz)和8gb内存的个人计算机上完成。(1)ieee-33节点测试系统光伏的视在功率极限为0.3mva。在16节点和33节点上安装ess，其充放电功率限制为0.3mw，而容量限制分别为0.15mwh和1.5mwh。1)基于拉格朗日对偶松弛的分布式算法效率通过应用第二节中的网络划分方法(ωm＝1，ωn＝0)，可以得到网络划分的结果，如图5所示。图6显示了ieee-33节点测试系统中的分布式算法每次迭代中的对偶间隙。可以看出原-对偶问题(g＝0)的最优解可以在96次迭代中求得，第一次迭代的对偶间隙明显大于最后一次迭代(96次迭代)的对偶间隙。在45次迭代后，收敛速度显著提高——这是因为解算器找到了一个接近最优解的解，从而使收敛加速到这个方向。因此，该分布式算法可以有效地应用于本发明提出的分布式电压控制策略中。2)不同网络划分方法的比较在这一小节中，我们比较了不同网络分区方法的结果。模块化函数、功率平衡和计算复杂度是本文考虑的三个指标，因此我们比较了其他两种不考虑功率平衡和计算复杂度的方法的结果。当比较不同的网络划分方法时，它们会产生不同的划分结果。因此，该电压控制模型在不同的网络划分方法下的计算时间和迭代次数是不同的。表1不同网络划分方法计算时间的比较方法迭代次数时间/s本文所提分区方法964.008不考虑计算复杂度的分区方法984.833不考虑功率平衡的分区方法1124.664不考虑网络划分-5.461从表1可以看出，采用本发明所提出的网络划分方法的分布式电压控制计算效率要优于不考虑计算复杂度的网络划分方法。这是因为当模型以分布式方式实现时，为了得到计算时间，子区域所花费的最长时间被认为是每个迭代过程中的计算时间，计算时间不包括相邻子区域之间通信的经过时间。因此，本发明所提出的网络划分方法的计算时间优于不考虑计算复杂度的网络划分方法。另外，不考虑功率平衡的分区方法在得到分布式电压控制结果时，迭代次数最大。这是因为当协调不同的子区域时，相邻子区域之间更复杂的功率交换需求(由于发电不足)导致了更多的迭代次数。因此，本发明提出的网络划分方法需要最少的计算时间和迭代次数。此外还可以看出，集中式电压控制模型由于计算量巨大需要花费更多的时间才能得到最优解。综上所述，本发明提出的网络划分方法更适合于分布式应用。3)dg容量曲线对电压控制的影响分析了dg容量曲线对电压控制的影响。在其他条件保持不变的情况下(例如，也考虑ess)，有/无容量曲线的电压偏差的结果如图7所示。从图7可以看出，考虑dg的容量曲线后，电压偏差可以显著减小。这是因为风电机组和pvg可以分担部分无功补偿需求。此外，dg产生的无功功率可以就地消耗，避免远距离传输，从而降低电压偏差。因此，考虑风电机组和pvg的容量曲线在电压控制中具有重要意义。4)ess对电压控制的影响本小节还分析了ess对电压控制的影响，在其他条件保持不变的情况下(例如，还考虑dg容量曲线)，图8显示了有/无ess的电压偏差结果。从图8可以发现，当考虑ess时，电压偏差大大减小，这也是因为本地ess有利于避免远程电力传输。而如图9所示，当考虑ess时，在16-18h期间，节点17处的电压幅值的平方保持在1.1236p.u.的上限。然而，在没有考虑ess的情况下，节点17处发生了电压越限。这是因为在这个时间间隔内，原本连接pvg的节点17处的电压幅值就即将达到其上限，此时任何额外的pv功率注入都将导致电压越限。在这种情况下，本地ess的充放电功率可以有效地降低pvg的注入功率，从而避免电压冲突。因此，ess有利于实现有效的电压控制。(2)实际的152节点系统本小节应用包含152节点的实际系统对该模型进行了测试。该系统的拓扑结构如图10所示。系统参数如表2所示，网络划分结果见表3：表2实际152节点系统参数表3实际152节点系统的分区结果区域节点区域节点区域节点区域1{6-11}区域6{47-53}区域11{91-99}区域2{1-5,12-15}区域7{54-62}区域12{100-108}区域3{16-24}区域8{63-71}区域13{109-123}区域4{25-37}区域9{73-75}区域14{124-128,142-152}区域5{38-46}区域10{76-90}区域15{129-141}值得说明的是，图11表明，实际系统中分布式算法的对偶间隙可以在167次迭代中收敛，而且与其他网络划分方法相比，该方法在实际系统中的分布式电压控制计算时间也最少。因此，基于拉格朗日对偶松弛的分布式算法和所提出的网络划分方法也可以应用于包含更多节点和分支的实际系统。值得说明的是，表4不同网络划分方法的计算时间对比方法迭代次数时间/s本文所提分区方法16714.669不考虑计算复杂度的分区方法17116.452不考虑功率平衡的分区方法22415.979不考虑网络划分-80.788值得说明的是，(3)ieee-8500节点测试系统ieee-8500节点测试系统被用来验证所提出的模型。该系统具有较大的负载或非线性，证明了该模型的优越性。该系统的拓扑结构如图12所示。如图13所示,应用于ieee-8500节点系统的分布式算法在每次迭代中的双间隙可以在561次迭代中收敛。此外，表5还表明，与其他网络划分方法相比，在该系统中采用该划分方法进行分布式电压控制的计算时间也是最少的，该方法可以减少一半的计算时间；表5不同网络划分方法的计算时间对比方法迭代次数时间/s本文所提分区方法56123.871不考虑计算复杂度的分区方法62350.379不考虑功率平衡的分区方法82431.294不考虑网络划分-276.416综上所述，本实施例的实施原理为：基于二阶锥松弛(secondorderconerelaxation,socr)的潮流约束，建立以总网损最小和节点电压幅值偏差最小为目标的电压控制模型。其中，我们分别利用容量曲线和定转子容量来限制pvg和wtg功率的可行域。然后，利用基于电气距离的模块化函数，提出了一种新型的考虑计算复杂度和功率平衡的网络划分方法，作为主动配电网分布式控制的前提。其中，利用优化模型中决策变量的个数和约束条件来量化计算复杂度。最后，建立一个基于拉格朗日对偶松弛的分布式模型，该模型不需要任何中心协调，只需要在边界子区域之间交换局部信息。边界子区域之间的交换功率被设置为边界变量，在进行局部优化时，可以等效地看作是辅助电源的功率注入。当前第1页12