用于控制具有N个开关单元的升压转换器的方法与流程

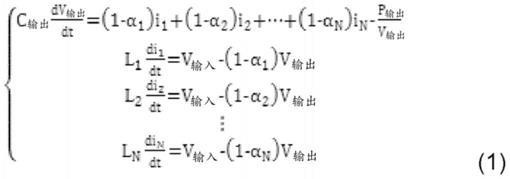
用于控制具有n个开关单元的升压转换器的方法
技术领域
1.本发明涉及一种用于控制具有n个开关单元的升压转换器的方法。
2.本发明涉及一种dc/dc升压转换器(boost converter)，也称为升压型转换器(step
‑
up converter)，是一种提升dc电压的转换器。


背景技术：

3.在机动车辆领域中，已知混合动力或电动升压转换器2用于包括电动牵引机4的电气组件10，如图1所示。
4.在这样的电气组件10中，升压转换器2被放置在电压逆变器3和电机4的上游，被认为是动态电流源。
5.然而，升压转换器2被定位在电源1和输入滤波器的下游。
6.升压转换器2是dc
‑
dc转换器。因此，其目的是向其供电的负载提供大于或等于在输入端处测得的电压的dc电压。
7.这种类型的转换器是非最小相位系统。具体地，将输出电压与控制操作联系起来的传递函数(表示为h(s))在复平面中表现为具有正实部的零。
8.通过关于给定的稳定操作点应用小信号模型和线性化，传递函数h(s)采用以下形式：
[0009][0010]
其中，z1＞0，p1＜0以及p2＜0分别是传递函数h(s)的零点和极点。
[0011]
另一方面，升压转换器2是非最小相位系统，其表现出的输出响应最初与输入变化相反。输出在向稳定点收敛之前趋于发散。这被称为输出电压的不同步阶段。此外，其各种状态(一方面)与控制操作(另一方面)之间的关系是非线性的。
[0012]
而且，一个普遍的问题是以稳定和快速的方式控制具有n个开关单元cell1至cell
n
的升压转换器(其中，n是非零自然数)，具体地是如图2所示的、其中开关单元由半导体(例如，mosfet)形成的同步升压转换器，而不是包含二极管的无源升压转换器。
[0013]
现有技术中特别值得注意的是文献us 2017/0257038 a1，该文献描述了一种用于控制具有n相的升压转换器的方法，其中，n是非零自然数。该方法旨在修改系统的开关频率并在各个单元的控制动作之间添加相位差，以避免dc母线的谐振频率。然而，这样的解决方案不能实现既稳定、动态又快速的控制。


技术实现要素：

[0014]
因此，本发明旨在使对升压转换器、更具体地是同步升压转换器的控制更稳定且更快。
[0015]
为此，提出了一种用于控制具有n个开关单元的同步升压转换器的方法，其中，n是非零自然数，所述升压转换器在输入端处从电压源接收dc电压并在输出端处向动态负载提
供大于或等于该输入电压的输出电压，该方法包括：
[0016]
‑
用于获取所述输入电压和输出电压的测量值的步骤；
[0017]
‑
用于获取在每个开关单元中测得的输入电流的步骤；
[0018]
该方法还包括：
[0019]
‑
用于根据所述输入电压、所述输出电压和所述测得的输入电流估计所述升压转换器中的总能量误差的步骤；
[0020]
‑
用于根据该总能量误差的所述估计值估计该升压转换器的输出功率值的变化的步骤；
[0021]
‑
用于根据该动态负载输出功率值的变化的所述估计值估计该升压转换器的所述动态负载输出功率值的步骤；
[0022]
‑
用于根据所述动态负载输出功率值计算每个开关单元的电流设定点的步骤；以及
[0023]
‑
用于根据所述计算出的电流设定点来控制每个开关单元的步骤。
[0024]
因此，该方法提供了实现一种控制操作，对于这种控制操作，估计的功率朝功率转换器的输入端处的总功率收敛。
[0025]
通过这种方法，可以将升压转换器的输出电压调整到用户设置的设定点电压，同时确保相对良好的系统稳定性，并优化控制系统对外部干扰的响应性和动态性。
[0026]
有利地并且以非限制性的方式，该升压转换器的动态负载输出功率值的变化是通过对该总能量误差的所述估计值的比例控制来估计的。这样，就可以得到相对快速且稳定收敛的估计值。
[0027]
有利地并且以非限制性的方式，该升压转换器的所述动态负载输出功率值(p
输出
)是通过对该总能量误差的所述估计值的比例积分控制来估计的。这样，就可以得到相对快速且稳定收敛的估计值。
[0028]
有利地并且以非限制性的方式，所述用于估计所述升压转换器中的总能量误差的步骤是该升压转换器的输入功率与动态负载输出功率之间的差值的函数，以及定义所述升压转换器的线性表示的输出向量的函数。这样，就可以获得总能量误差的相对可靠的估计值。
[0029]
有利地并且以非限制性的方式，对于每个开关单元，根据所述开关单元的电感值与在所述相应开关单元中测得的输入电流的平方的乘积的离散和，以及根据该升压转换器的输出电容值与所述输出电压的平方的乘积，来计算所述输出向量。因此，可以相对快速和可靠地确定形成升压转换器线性化的输出向量。
[0030]
本发明还涉及一种电气组件，该电气组件包括dc电源、具有n个开关单元的升压转换器、dc/ac电压转换器、电机、以及用于所述升压转换器的适用于实施如前文所述的方法的控制装置。
[0031]
本发明还涉及一种包括这样的电气组件的机动车辆。
附图说明
[0032]
在参照附图阅读通过指示而非限制性方式给出的本发明的具体实施例的以下描述时，本发明的其他特征和优点将会变得更清楚，在附图中：
[0033]
[图1]是根据本发明的电源组件的原理图；
[0034]
[图2]是根据本发明的第一实施例控制的具有n相的升压转换器的示意图，其中，n是非零自然整数、在这种情况下大于3；
[0035]
[图3]是升压转换器的开关单元及其每种工作模式的等效电路的示意图；
[0036]
[图4]是升压转换器的每个开关单元的输入端处的电流设定点的估计器的图解表示。
具体实施方式
[0037]
在本发明的第一实施例中，参考图1至图4，描述了一种通过精确反馈线性化对具有n个开关单元cell1至cell
n
的升压型转换器进行非线性控制的方法。
[0038]
参考图2，每个开关单元cell1至cell
n
包括两个控制开关s1至s
n
和至以及电感l1至l
n
。
[0039]
该方法用于补偿要控制的系统表现出的非线性。
[0040]
这种补偿的形式与该系统的结构有关。举例来说，为了通过减法来补偿非线性项(表示为θ(x))，该系统的输入端处的控制向量u和非线性项θ(x)必须以加法u+θ(x)的形式一起出现。
[0041]
另一方面，为了通过除法来补偿θ(x)，控制向量u和非线性项必须以乘法u
·
θ(x)的形式一起出现。
[0042]
具有n个开关单元的升压转换器2的方程如下：
[0043][0044]
方程(1)可以用仿射非线性方程的一般形式表示如下：
[0045][0046]
因此，方程(2)变为：
[0047][0048]
其中，
[0049]
·
x∈r
n
＝(i
1 i
2 ... i
n v
输出
)
t
为系统状态变量的向量，
[0050]
·
u(t)＝(α1ꢀ…ꢀ
α
n
)∈r
m
表示被视为到该系统的输入的控制向量，α
k
是施加到第k个开关单元的开关s
k
的占空比，并且1
‑
α
k
是施加到第k个开关单元的开关的占空比。
[0051]
·
f(x)和g(x)是无限可导的非线性函数；
[0052]
·
(l1，l2，...，l
n
)和c
输出
分别是每个开关单元的电感和升压转换器的输出端处的
电容；
[0053]
·
i1，i2，...，i
n
和v
输出
分别是每个电感中的电流和升压转换器2的输出电压；
[0054]
·
p
输出
是在输出端处连接到升压转换器2的动态负载的功率。
[0055]
以下在描述中，参考图3和图4，将仅针对单个开关单元描述升压转换器2。
[0056]
升压转换器2，也称为升压器2，具有两种工作模式：第一模式31，在该第一模式中，升压器2的电感l1充电，而输出端处的电容器c
输出
放电；以及第二模式32，在该第二模式中，升压器2的电感l1放电，而输出端处的电容器c
输出
充电。
[0057]
第一模式31受以下电气方程制约：
[0058][0059]
关于该第一模式31中的能量变化，储存在电感中的能量的方程的形式为因此，该能量随时间的变化采用以下形式：
[0060][0061]
此外，储存在电容器中的能量的方程的形式为因此，该能量随时间的变化采用以下形式：
[0062][0063]
第二模式32受以下电气方程制约：
[0064][0065]
在这种模式下的能量变化方面：
[0066]
‑
储存在电感中的能量随时间的变化采用以下形式：
[0067][0068]
‑
储存在电容器中的能量随时间的变化采用以下形式：
[0069][0070]
因此，系统中储存的总能量的变化，表示为e
t
，为：
[0071][0072]
并且：
[0073]
[0074]
通常，对于具有n个开关单元的转换器的情况，以下输出向量提供系统的整体线性化：
[0075][0076]
方程(12)的一阶导数给出以下方程：
[0077][0078]
现在，方程(13)对应于系统中总能量随时间的变化，其表示由转换器耗散的损耗。
[0079]
寻求的是估计dc/dc转换器吸收的总电流的设定点现在，对于效率为η的功率转换器，根据功率守恒定律，可得到以下结果：
[0080][0081]
其中，并且
[0082]
因此，输入电流变为：
[0083][0084]
因此，获得了以下方程组：
[0085][0086]
其中，
[0087]
p
min
≤p
输出
＝∫σ
·
dτ≤p
max
ꢀꢀꢀ
(17)
[0088]
分为下两种情况：
[0089]
‑
在瞬时状态下：σ≠0和p
输出
是变量；
[0090]
‑
在稳定状态下：σ＝0和p
输出
是常数。
[0091]
另一方面，取表达式(13)；这由两项组成：
[0092]
第一项表示转换器吸收的总功率。输入电压和电感中的电流是使用传感器物理测量的两个变量。因此，转换器吸收的总功率是已知的。
[0093]
第二项p
输出
表示负载吸收的有用功率。该有用功率无法测量，但可以估计。因此，它表示为
[0094]
因此，得到方程
[0095][0096]
因此，估计误差将为：
[0097][0098]
当时：
[0099][0100]
通过将方程(16)表示为估计误差的函数，得到以下结果：
[0101][0102]
并且
[0103][0104]
其中，k1和k2是要确定的观测器的增益。
[0105]
应当注意，这些方程采用luenberger(龙伯格)观测器的形式，其中已经包括了估计误差项
[0106]
该项的目的是随着时间的推移使估计状态趋近真实状态。
[0107]
对于方程(22)，经过适当的展开之后：
[0108][0109]
对于方程(21)，经过适当的展开之后：
[0110][0111]
其中，
[0112][0113]
方程(25)表示功率转换器中的总能量误差，即输出y与其估计值之间的差值，其中，y是表示系统中储存的能量的向量。
[0114]
方程(2)用于确定估计功率是使用比例积分控制器作用于误差获得的。
[0115]
因此，在稳定状态下，误差朝零的稳定渐近收敛给出：
[0116][0117]
其中，
[0118]
因此，对于给定的操作点：
[0119][0120]
因此，方程的导数意味着(27)：
[0121][0122]
并且，因此：
[0123][0124]
通过这种方法，估计率会朝由功率转换器吸收的总输入功率收敛。
[0125]
因此，系统效率的概念在这种方法中消失了，并且输入端处的设定电流朝以下表达式收敛：
[0126][0127]
因此，每个开关单元k中的设定点电流由下式给出：
[0128][0129]
观测器的增益k1和k2然后由以下方程确定
[0130][0131]
其中，w
n
＝2πf
n
是估计器的通带，其中，例如f
n
＝[100hz；600hz]和ξ＞0是阻尼因子。
[0132]
因此，对于k1和k2的正值，获得误差的朝零的稳定渐近收敛。