电动机控制装置及其自动调整方法与流程

1.本发明涉及电动机控制装置以及电动机控制装置的自动调整方法。


背景技术：

2.在对控制对象的机械进行控制的电动机控制系统中，存在由于机械的共振特性而使电动机端、机械端振动，而无法实现所希望的响应特性的情况。在这样的情况下，在控制器后级使用陷波滤波器或加工控制指令等对策是有效的，但这需要掌握机械的共振特性。
3.在fa领域中，在导入电动机控制系统时、控制对象机械的维护后等需要电动机控制系统的调整，但存在缩短该调整时间、提高生产率的需求。另外，使调整所涉及的人工成本最小化也是需求之一。从这样的背景出发，近年来在fa领域中，要求电动机控制系统的短时间的、或者实时的自动调整技术。
4.在由于机械的共振特性而无法获得所希望的响应特性的情况下，为了在短时间内自动调整承担对其进行抑制作用的控制单元(陷波滤波器等)，需要在短时间内自动地掌握、辨识机械的共振特性。
5.作为短时间且自动地掌握作为机械的谐振特性之一的谐振频率的技术，提出了专利文献1。另外，非专利文献1提出作为根据主分量由正弦波信号构成的信号来逐次推定正弦波信号的频率的方法。
6.专利文献1的技术如图14所示。在专利文献1中，提出了如下方法：在由速度控制单元101和转矩控制单元103控制与负载110连接的电动机109的控制系统中，在速度控制单元101的后级设置第一陷波滤波器102，通过自动调整第一陷波滤波器102的陷波频率来抑制由速度检测单元108检测出的电动机端的速度响应(电动机转速)的振动。
7.专利文献1的陷波频率的自动调整方法为通过高通滤波器104从电动机的旋转速度提取振动分量。并且，通过陷波滤波器系数修正单元107将使用与第一陷波滤波器独立地准备的第二陷波滤波器106对振动分量进行处理后的信号和通过方向滤波器105对振动分量进行处理后的信号进行乘法运算，并基于乘法运算结果逐次更新/推定振动分量的频率，将其作为陷波频率而应用于第一陷波滤波器102。推定图14记载的振动分量的频率的从y到w的处理能够解释为自适应陷波滤波器的一个方式。
8.在非专利文献1中，提出了运算简单的离散iir(infinite impul response：无限脉冲响应)型的自适应陷波滤波器的算法。
9.现有技术文献
10.专利文献
11.专利文献1：日本特开2004-274976号公报
12.非专利文献1：adaptive iir filtering in signal processing and control，marcel dekker，inc.，1995，pp.554-599。


技术实现要素：

13.发明所要解决的课题
14.然而，在专利文献1中，存在以下课题：在逐次更新/推定振动分量的频率时，分别需要第二陷波滤波器106和方向滤波器105的运算且在运算成本方面不优异。另外，在逐次更新时，存在更新量(各次更新的量)依赖于振动分量的振幅大小，通过逐次更新而得到的振动分量的频率的推定值不稳定地收敛的情况、收敛需要时间这样的问题。进而，在逐次更新中得到的振动分量的推定值不稳定地收敛而作为推定值可靠度低的状况下，也将振动分量的推定值作为陷波频率应用于第一陷波滤波器，有可能无法发挥振动抑制的效果。
15.在非专利文献1的算法中，在利用进行固定小数点运算的廉价的运算装置实现标准化(normalization)处理的情况下，特别是陷波频率越是低频，则在标准化处理中越有可能发生运算溢出(oveflow)，存在无法正确地进行逐次更新(逐次更新处理失败)这样的课题。
16.本发明是鉴于这样的课题而完成的，其目的在于提供一种电动机控制装置及其自动调整方法，即使是进行固定小数点运算的廉价的运算装置，也能够不依赖于振动分量的振幅的大小且不担心运算溢出而能够稳定/可靠地逐次更新/推定为了自动调整抑制机械的共振特性的控制单元而需要的、振动分量的频率的推定值。
17.用于解决课题的手段
18.为了解决所述课题，举出本发明的“电动机控制装置”的一例，为一种电动机控制装置，具有自动调整装置，该自动调整装置基于与电动机控制系统的响应重叠的振动分量的频率，对所述电动机控制系统中包含的控制器进行自适应调整，所述自动调整装置有如下部分构成：振动提取部，其将所述电动机控制系统的响应作为输入，从所述电动机控制系统的响应提取振动分量；陷波滤波部，其将由所述振动提取部提取出的振动分量作为输入；编码部，其将由所述陷波滤波部计算出的所述陷波滤波部的内部状态量作为输入；限幅部，其将由所述陷波滤波部计算出的所述陷波滤波部的输出作为输入；自适应更新部，其将所述编码部的输出和所述限幅部的输出作为输入；以及单位转换部，其将所述自适应更新部的输出作为输入，所述编码部仅提取并输出所述内部状态量的符号的信息，所述限幅部计算并输出限制了所述陷波滤波部的输出的振幅的信息，所述自适应更新部基于所述编码部的输出与所述限幅部的输出相乘而得的值，逐次更新并输出所述陷波滤波部的滤波参数即陷波频率的推定值，所述陷波滤波部逐次地采用所述自适应更新部逐次计算/输出的所述推定值作为所述陷波频率，所述单位转换部将所述自适应更新部逐次计算出的所述推定值的单位转换为赫兹并将其作为推定值输出，所述自动调整装置使用所述推定值，对所述电动机控制系统中包含的所述控制器进行自适应地调整。
19.发明效果
20.根据本发明，通过用编码部对陷波滤波部计算出的陷波滤波部的内部状态量进行处理，并通过限制器部对陷波滤波部的输出进行处理，而不需要标准化处理，进而采用收敛判定部，由此能够避免运算溢出，并且能够进行高可靠性的振动分量的频率的逐次更新/推定，能够在短时间内自动调整控制器。
附图说明
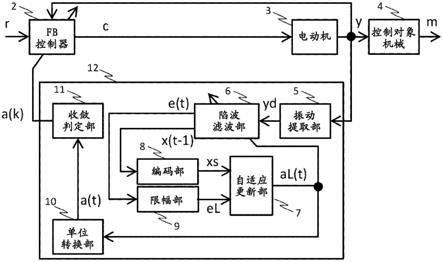
21.图1是表示实施例1的电动机控制装置的基本结构的图。
22.图2是表示fb控制器的一例的图。
23.图3是表示自动调整装置的一例的图。
24.图4是表示自适应陷波滤波器的一例的图。
25.图5是表示图4的自适应陷波滤波器的频率特性的图。
26.图6是表示xz/ez的频率特性的图。
27.图7是表示xz的频率特性的图。
28.图8是表示收敛判定部的图。
29.图9是表示实施例1的更新情况的图。
30.图10是图9的放大图。
31.图11是实施例1的电动机控制装置的自动调整的动作流程图。
32.图12是表示实施例2的电动机控制装置的基本结构的图。
33.图13是表示实施例3的电动机控制装置的一例的图。
34.图14是表示专利文献1所记载的电动机的控制装置的图。
具体实施方式
35.以下，参照附图对应用了本发明的实施例进行说明。
36.另外，在各图中，对具有共同的功能的构成要素赋予相同的编号，并省略其重复的说明。另外，以下有时将“反馈”简记为“fb”，将“陷波滤波器”简记为“nf”，将“低通滤波器”简记为“lpf”，将“高通滤波器”简记为“hpf”，将“带通滤波器”简记为“bpf”。
37.实施例1
38.图1表示将本发明的实施例1的自动调整装置12应用于一般电动机的fb控制系统的结构。
39.fb控制器2的操作量c被提供给电动机3，通过电动机3的输出y对控制对象机械4进行驱动控制。另外，为了简化，在图1中省略了电流控制系统的记载。
40.输出y是电动机转速[rpm]，使用传感器(例如编码器)对其进行测量，fb控制器2根据输出y的测量值和转速指令r计算操作量c，并输出到电动机3。
[0041]
在图1的fb控制系统中，fb控制器2具有以下单元：在输出y成为振动的情况下(即电动机端成为振动的情况下)，通过掌握输出y的振动分量的频率来抑制输出y的振动分量的单元；或者在输出y成为振动的情况下，通过掌握输出y的振动分量的频率来抑制控制对象机械4的输出m的振动分量的单元。
[0042]
自动调整装置12掌握/推定输出y的振动分量的频率，基于振动分量的频率的推定值，自动地调整fb控制器2所具有的抑制输出y的振动分量的单元、或者fb控制器2所具有的抑制控制对象机械4的输出m的振动分量的单元。
[0043]
作为具备抑制输出y的振动分量的单元的fb控制器2的一例，是在fb控制环路内内置陷波滤波器(以后将其称为“实际陷波滤波器”)的、如图2所示的fb控制器21。
[0044]
在图2中，fb控制器21在控制对象具有共振特性、电动机端因共振特性而振动的情况下，抑制该振动。具体而言，通过将实际陷波滤波器23的陷波频率设定为与控制对象的共
振频率一致，实际陷波滤波器23的零点抵消共振特性的共振极，fb控制器21抑制振动。
[0045]
在该例子中，fb控制器21为了抑制振动而需要准确地掌握控制对象的共振频率。
[0046]
本发明的自动调整装置12通过推定电动机端的振动分量的频率，能够自动地调整图2所示的fb控制器21(具体而言，实际陷波滤波器23)，抑制电动机端的振动。
[0047]
作为自动调整装置12的实现单元，考虑图3的自动调整装置31。具体而言，自动调整装置31由hpf32和自适应陷波滤波器(anf：adaptive notch filter)33构成，通过对输出y应用hpf32来提取振动分量yd，对yd应用anf33，将anf33计算出的陷波频率的推定值a(其中单位为[hz])作为自动调整装置31的输出。
[0048]
作为anf33的一例，图4以及以下示出具有与非专利文献1所记载的内容相同的能力的、能够以简单的处理实现的离散iir型的anf。
[0049]
在该例中，anf41由数式(1)所示的点阵形式(lattice form)的离散iir(infinite impulse response无限脉冲响应)型陷波滤波器42和基于数式(2)、(3)的自适应调整部43构成，anf41将振动分量yd(t)作为输入，输出振动分量yd(t)的频率在时刻t的推定值al(t)。数式(4)的单位转换部10是仅将推定值al(t)的单位转换为[hz]的处理，与anf41的al(t)的推定性能没有直接关系。
[0050]
《离散iir型陷波滤波器42》
[0051]
[数式1]
[0052][0053]
《自适应调整部43》
[0054]
[数式2]
[0055][0056]
[数式3]
[0057][0058]
《单位转换部10》
[0059]
[数式4]
[0060]
a(t)＝arecas(-a
l
(t))/(2πts)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0061]
在此，数式(1)是将对[x(t-2)x(t-1)]进行转置而得到的值作为状态矢量的状态空间表现，x(t)是由离散iir型陷波滤波器42计算出的内部状态量，e(t)是由离散iir型陷波滤波器42计算出的输出。另外，μ、λ、r、ts和σx2(t)分别是更新步骤调整系数、忘却系数、数式(1)的陷波宽度、采样周期以及x的方差在时刻t的推定值，都是正值。
[0062]
振动分量的频率的推定通过数式(2)的al(t)的逐次更新来进行，时刻t的al(t)的更新量由数式(2)的右边第二项来给出。数式(2)的右边第二项基于数式(1)的离散iir型nf42的内部状态量x(t-1)与离散iir型nf42的输出e(t)之积而构成，al(t)的更新量的正负
由e(t)
·
x(t-1)决定。在anf41中，在推定值的逐次更新中利用通过数式(1)的离散iir型nf42的运算得到的内部状态量x(t-1)，而不需要另外设置相当于专利文献1的方向滤波器105的滤波器，因此能够降低与x(t-1)的计算相关的运算成本。
[0063]
数式(3)用于进行标准化处理，即，使基于数式(2)的al(t)的逐次更新稳定且平滑，并且排除作为输入的振动分量yd(t)的振幅的大小对更新量(数式(2)的右边第二项)的依赖性。用在数式(3)中得到的σx2(t)除e(t)
·
x(t-1)，进行标准化处理。
[0064]
以下对更新量的正负由e(t)
·
x(t-1)决定以及数式(3)作为标准化处理有效地发挥功能的情况进行详细说明。
[0065]
图5表示离散iir型陷波滤波器中的从yd(t)到e(t)的传递特性ez、以及从yd(t)到x(t-1)的传递特性xz的频率特性(波特图)。另外，在该图中，实线表示ez，虚线表示xz，a是将数式(1)中的al的单位转换为[hz]后的值，在图5中，a＝1000[hz]。
[0066]
现在，振动分量yd(t)如下数式那样由正弦波与噪声之和来表现。
[0067]
[数式5]
[0068]
yd(t)＝a sin(2π
·
fd·
t)+v(t)，a＞0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0069]
其中，a、fd分别为正弦波的振幅、频率[hz]，为了简单，v(t)设为平均0、方差σv2(其中a＞＞σv2)的白噪声。
[0070]
如果关注图5的相位特性，则可知ez和xz的相位特性在比频率a[hz]小的区域完全相同，在比频率a大的情况下，ez的相位特性与使xz的相位特性超前180[deg]的特性相同。
[0071]
现在，为了简单，对于视为v(t)＝0，yd(t)的正弦波的频率fd，考虑(i)fd＜a和(ii)fd＞a的情况。
[0072]
anf41的目的在于，推定使a与fd一致、即振动分量的频率fd。为了形成该关系，在处于(i)的关系的情况下，使a减少，在处于(ii)的关系的情况下使a增加即可。这样的a的更新的增减(正负)能够基于e(t)
·
x(t-1)来决定。具体而言，根据图5所示的ez与xz的关系可知，在(i)的情况下，e(t)和x(t-1)相对于yd(t)为同相，因此e(t)
·
x(t-1)始终为正，在(ii)的情况下，e(t)和x(t-1)相对于yd(t)为相反相位，因此e(t)
·
x(t-1)始终为负。将e(t)
·
x(t-1)这样的特征用于a的更新的增减(正负)的决定的是数式(2)。
[0073]
另外，e(t)与x(t-1)的关系可以用以下数式表示。
[0074]
[数式6]
[0075][0076]
此外，αx是振动分量的频率为fd[hz]且数式(1)的陷波频率为a[hz]时的相当于传递特性xz/ez的增益的常数。图6示出传递特性xz/ez的频率特性。
[0077]
αx根据fd与a的关系变化而变动，注意与振动分量yd(t)的振幅a、e(t)的振幅以及x(t-1)的振幅无关的点。另外，注意到存在与anf41的逐次更新相关的fd或a的变动的频率越高，αx的变动的频率越高的倾向。
[0078]
若将数式(6)代入数式(3)并进行整理，则得到以下数式。
[0079]
[数式7]
[0080][0081]
其中，z是z转换中的z算子。
[0082]
进而，若将数式(6)及数式(7)代入数式(2)并整理，则数式(2)的右边第二项的更新量可写成以下数式。
[0083]
[数式8]
[0084][0085]
数式(8)表示更新量非依赖于yd(t)、e(t)以及x(t-1)的振幅的大小而基于αx来决定。另外，lpf(λ)是截止频率为fc[hz]的离散型1次延迟系统的低通滤波器。例如，在λ＝0.99、ts＝100[μs]的情况下，lpf(λ)的截止频率为fc≈16[hz]。在anf41的逐次更新中，例如由于噪声v的影响等，即使假设αx的变动的频率变高，由于lpf(λ)除去αx的变动的高频分量，所以数式(8)的更新量的变动成为除去了高频分量的值，数式(2)所示的由逐次更新引起的al的变化变得平滑。
[0086]
根据图6所示的传递特性xz/ez的频率特性，fc越接近a，则αx为越大的值，因此数式(8)所示的更新量，fc越接近a则越微小，向a的真值fd的收敛变得稳定。
[0087]
由此可知，数式(1)～(3)所示的anf41具有数式(2)所示的al的逐次更新根据数式(3)而不依赖于振动分量的振幅而变得稳定且平滑的优点。
[0088]
然而，在进行固定小数点运算的运算装置中执行数式(1)～(3)的anf41的情况下，特别是在数式(3)的运算中产生运算溢出，可能会破坏数式(2)的al的逐次更新。作为推定对象的振动分量yd的频率越低，这变得越显著。
[0089]
以下说明其理由。
[0090]
图7是表示使数式(1)所示的陷波滤波器的xz的al变化时的频率特性的图。可知xz在al越成为低频，在al周边和al以下的频带中会有增益越显著化的倾向。即，al越低，al的更新所需的x(t-1)越趋于显著。因此，在用于固定小数点运算的比特数不充分的情况下，在计算x(t-1)时可能会发生运算溢出。
[0091]
为了避免这样的运算溢出，考虑对作为输入的yd(t)事先乘以常数增益，减小yd(t)的振幅。但是，在这样的方法中，在固定少数点运算中，导致yd(t)失去原本具有的量化所伴随的分辨率(由于粗糙的量化，振动波形变得不平滑等)，没有解决本质的课题。
[0092]
x(t-1)可能运算溢出，这是因为x(t)也有可能运算溢出。
[0093]
在数式(3)的σx2的计算中，为了更新σx2，需要x(t)的平方，进而需要将其逐次相加。因此，在数式(3)的运算中，发生运算溢出的可能性非常高，这导致数式(1)～(3)的anf41的逐次更新被破坏的可能性非常高的问题。
[0094]
此外，注意在数式(2)中，特别是具有在低频显著增大趋势的x(t-1)除以同样具有
显著增加倾向的σx2，更新量不显著这点。这是由于数式(1)～(3)的anf41包括基于数式(3)的标准化处理。
[0095]
al表示数式(1)的anf的陷波频率，同样地表示陷波频率的以单位[hz]提供的a是根据数式(4)的关系提供的。
[0096]
即，a是基于al的余弦函数的非线性映射，其取值范围是[-1，1]。在陷波频率al低的情况下，根据余弦函数的非线性，a成为接近-1的值，al的每单位赫兹的变化量越是在低频则越微小。这表示在使用数式(2)来推定振动分量yd的频率的情况下，振动分量yd越是低频，每单位赫兹的更新量(右边第二项)必须越微小。数式(1)～(3)的anf41包含标准化处理，其更新量不依赖于振动分量yd的振幅a，但如数式(8)所示，依赖于αx，数式(8)的更新量微小，因此更新步骤调整系数μ需要选择小的值。
[0097]
为了解决所述数式(1)～(3)的anf41所具有的所述的溢出问题，在本发明中提出了图1所示的自动调整装置12。
[0098]
自动调整装置12中的al的更新基于以下数式。
[0099]
[数式9]
[0100]al
(t+1)＝a
l
(t)-μ
p
·
l(|e(t)|)
·
sign(e(t)
·
x(t-1))
ꢀꢀꢀꢀꢀꢀꢀ
(9)
[0101]
此外，μp是自动调整装置12中的更新步骤调整系数，sign(
·
)是符号函数，l(
·
)是以下数式所示的限制函数。
[0102]
[数式10]
[0103][0104]
其中，up、ud分别为限制上限及限制下限。另外，为了以后简单，假定ud＝up。
[0105]
在数式(9)中，通过sign(e(t)
·
x(t-1))得到al的更新方向的信息，通过l(|e(t)|)基于e(t)的振幅得到更新量的增益。
[0106]
在数式(9)中，不需要计算数式(3)的σx2，因此数式(9)能够避免由σx2引起的运算溢出产生的问题。因此，数式(9)只要能够避免x(t-1)的计算中的运算溢出，就能够针对al的逐次更新解决运算溢出的问题。为了避免x(t-1)的运算溢出的发生，一个是增加用于固定小数点运算的比特数。
[0107]
在数式(9)中，不包含σx2的理由是，通过设为sign(e(t)
·
x(t-1))，舍去e(t)和x(t-1)的振幅的信息。σx2的标准化处理虽然使al的更新量不依赖于振动分量的振幅的大小，但在sign(e(t)
·
x(t-1))中也同样地能够使al的更新量不依赖于振动分量的振幅的大小。
[0108]
基于σx2的标准化处理的优势之一是，如图6所示，在真值fd周边αx变大，更新量变得微小，逐次更新导致的收敛性稳定化。为了模拟地得到该优势，在数式(9)中采用l(|e(t)|)。
[0109]
如图5的ez的频率特性所示，在陷波频率a[hz]远离振动分量yd的频率的情况下，e(t)的振幅与振动分量yd的振幅大致相等，但在陷波频率a[hz]接近振动分量yd的频率的情况下，具有e(t)的振幅变小的性质。即，e(t)的振幅由于在真值fd周边变小的性质，因此能
够期待起到与标准化处理中的αx类似的作用。
[0110]
另外，l(|e(t)|)减轻对振动分量的振幅的大小的依赖性，使μp的设计变得容易。振动分量yd的振幅的容许上限根据应用而不同，例如在电动机控制中，yd的单位为[rpm]，假设将其上限设为100[rpm]，则al可取的范围必须为[-1，1]，并且受到在低频中更新量必须精细的限制，因此如果在数式(9)中不使用限幅函数l(|e(t)|)而仅设为|e(t)|，则必须根据e(t)可取的上限值(在该例子中为100[rpm])而将μp设定得较小。在该情况下，会牺牲更新的速度。如果为了加快收敛而将μp设定得较大，则在|e(t)|较大的情况下al的逐次更新会振动，从而无法顺利地进行推断。
[0111]
在数式(9)中，通过使用限幅函数l(
·
)解决了与这样的μp的设定相关的权衡的问题。即，通过对|e(t)|实施l(
·
)，|e(t)|的大小被限制，能够与限制上限、下限up、ud相匹配地设计μp，能够解决在维持更新速度的同时，在|e(t)|大的情况下可能发生的逐次更新成为振动的问题。
[0112]
在数式(9)中，表示更新量的右边第二项能够如以下那样变形。
[0113]
[数式11]
[0114][0115]
因此，图1所示的自动调整装置12成为由以下的数式(12)～(14)给出的简单的结构。
[0116]
《自适应更新部7》
[0117]
[数式12]
[0118]al
(t+1)＝a
l
(t)-μ
p
·el
(t)
·
xs(t-1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
12)
[0119]
《编码部8》
[0120]
[数式13]
[0121]
xs(t-1)≡sign(x(t-1))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
13)
[0122]
《限幅部9》
[0123]
[数式14]
[0124]el
(t)≡l(e(t))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(14)
[0125]
另外，陷波滤波部6及单位转换部10进行数式(1)及数式(4)的处理，振动提取部5例如设为hpf即可。另外，振动提取部5也可以同时瞄准传感器噪声的去除而设为bpf。
[0126]
在本发明中，限幅部作为最简单的数式(14)，但除了数式(14)所示的以外，也可以是提取e(t)的振幅以及符号的信息的其他单元。
[0127]
本实施例的自动调整装置12的数式(9)(等价地，数式(12)～(14))的有效性如图9、图10所示。图9、10是(a)数式(1)～(3)的情况、(b)数式(9)的情况以及(c)数式(1)～(3)中除去了标准化处理的情况(即，始终设为σx2＝1)的逐次更新引起的a[hz]的收敛状况。振动分量yd是噪声v＝0、振幅a为3.5和5.0的情况下的a[hz]的收敛状况。另外，将真值fd设为800[hz]。
[0128]
图9(f)使用的2种振动分量yd、图9(a)、图9(b)以及图9(c)分别为(a)数式(1)～(3)的情况、(b)数式(9)的情况以及(c)数式(1)～(3)中除去了标准化处理的情况下的a
[hz]的收敛状况。在(a)、(b)中，能够掌握不依赖于振动分量yd的振幅而将收敛速度保持为大致恒定。(b)获得这样的结果的原因在于，通过μp
·
l(|e(t)|)维持速度，并设为l(|e(t)|)
·
sign(e(t)
·
x(t-1))，由此排除了对振动分量的振幅的依赖性。
[0129]
图10是将图9放大后的图。图10(i)和(ii)分别是振幅a＝3.5时的(a)～(c)的结果以及振幅a＝5.0时的(a)～(c)的结果。根据图10可知，(a)根据标准化处理的效果，a平滑地收敛，但(c)由于不包含标准化处理，因此收敛时成为振动。另外，可知(b)由于l(|e(t)|)与标准化处理的αx具有类似的作用，因此收敛时的振动现象减轻。
[0130]
基于σx2的标准化处理的优势点之一包含lpf(λ)，逐次更新变得平滑，收敛变得稳定。
[0131]
数式(9)不包含lpf(λ)，不具有lpf(λ)带来的优势。因此，例如由于噪声v(t)的影响等，有可能基于逐次更新的al不平滑，收敛不稳定。在振动分量yd如数式(5)所示的(其中，v(t)＝0)那样未以单一的正弦波赋予的情况下有产生这种现象的倾向。
[0132]
另外，虽然可以说是所有anf，但需要通过逐次更新来判别推定值al是否渐近收敛于真值fd，并达到了推定完成的手段。
[0133]
针对这样的课题，在本发明中设置收敛判定部11。
[0134]
收敛判定部11考虑各种实现方法，但在图8以及以下示出简单的结构的一例。
[0135]
《收敛判定部11》
[0136]
差分过程由以下数式定义。
[0137]
[数式15]
[0138]
ε(t)≡|a(t)-a(t-1)|
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(15)
[0139]
收敛判定脉冲计算部81基于数式(15)，通过以下的逻辑计算收敛判定脉冲pls(k)。
[0140]
(i)在差分过程ε(t)在指定时间te以内一次都没有超过差分阈值tε且指定时间te内的a(t)的最初值与最后值的差(斜率)的绝对值在斜率阈值tεd以内时，判断为收敛，将该时刻设定为t＝k，将收敛判定脉冲pls(k)设定为1。
[0141]
(ii)在差分过程ε(t)在指定时间te以内超过一次差分阈值tε，或者在收敛判定脉冲发生后，在经过指定时间ted前收敛判定脉冲pls(t)为0。
[0142]
最终，如图8所示，收敛判定部11在相对于a(t)成为收敛判定脉冲pls(k)＝1的时刻t＝k时，判断为得到了可靠的a(t)推定值，并输出推定值序列a(k)。因此，在不产生收敛判定脉冲的情况下，不输出a(k)，自动调整装置12不进行fb控制器2的调整。
[0143]
通过设置简单的斜率运算方法以及斜率阈值，始终不对a(t)以相同符号持续微小地变化的情况(即到达收敛的中途过程的情况)进行收敛判定。另外，也包含如下的设计：将在指定时间te的a(t)的变化(斜率)用于收敛判定的评价，即使是a(t)不会平滑地变化，稍微振动，如果在指定时间te的a(t)的变化(斜率)小，则作出收敛判定。
[0144]
由此，即使在数式(9)不包含lpf(λ)而逐次更新引起的al变得不平滑的情况下，自动调整装置12也能够在适当的时刻输出高可靠性的推定值a(k)，收敛判定部11发挥针对数式(9)不包含lpf(λ)的缺点的恢复(recovery)作用。
[0145]
另外，收敛判定部11具有以下这样的优越性。
[0146]
如果振动分量yd为单一的正弦波，则在al收敛于振动分量的频率fd的情况下，e
(t)＝0，因此能够以具有陷波滤波部6的输出e(t)的振幅的大小来判断al是否渐近/收敛于振动分量的频率fd。
[0147]
然而，在振动分量yd包含如数式(5)所示的噪声v(t)且方差σx2大的情况下，即使假设a＝fd，e(t)的振幅也显著地残留，不容易以e(t)的振幅的大小来判断收敛完成。
[0148]
此外，在处理叠加有多个正弦波的振动波形的情况下，即使假设a＝fd，其他的正弦波分量也被输出到e(t)，e(t)的振幅仍然显著地残留，在该情况下，也不容易以e(t)的振幅的大小来判断收敛完成。
[0149]
正弦波的重叠的数量依赖于控制对象机械4的特性，只要不事先调查控制对象机械4的特性，正弦波的重叠的数量是未知的。基于该情况，基于e(t)的收敛完成的判定也不能说是优选的方法。
[0150]
另一方面，收敛判定部11在振动分量yd包含噪声且多个正弦波分量重叠的情况下，在陷波滤波部6的al进行了收敛的情况下，在能够正确地判定这一点上是优异的，可以说在通过fb控制器2驱动图1的控制对象机械4那样的电动机控制系统的自动调整装置12中是优势的单元。
[0151]
进而，实际的振动波形不是振幅恒定的理想正弦波，振动波形是近似的正弦波，关于振幅有衰减。对于这样的波形，在应用数式(1)～(3)的anf、或者本实施例的自动调整装置12(伴随数式(9))时，逐次更新中的al的收敛不保证成为图9、图10所示那样的稳定的收敛。在这样的实用事例中，收敛判定部11是有用的，即使逐次更新中的al的收敛稍微振动，或者是偶尔(時折)振动，收敛判定部11也能够提取一定期间收敛的时刻的a作为能够信赖的推定值。从该观点出发，具备收敛判定部11的自动调整装置12在通过fb控制器2驱动图1的控制对象机械4那样的电动机控制系统的自动调整装置12中也可以说是优势的单元。
[0152]
由陷波滤波部6、自适应更新部7、编码部8、限幅部9、收敛判定部11等构成的自动调整装置12能够通过由cpu将预定的程序载入到存储器上，并且cpu执行载入到存储器上的预定程序来实现。
[0153]
图11表示实施例1的自动调整装置的自动调整的动作流程。
[0154]
在s101中，通过振动提取部5从电动机控制系统的响应中提取振动分量。
[0155]
在s102中，向陷波滤波部6输入振动分量，计算陷波滤波部6的内部状态量x及输出e。
[0156]
在s103中，通过编码部8仅提取内部状态量x的符号的信息并输出。
[0157]
在s104中，通过限幅部9计算并输出限制了输出e的振幅的信息。
[0158]
在s105中，通过自适应更新部7，基于编码部8的输出与限幅部9的输出相乘后的值，逐次更新并输出陷波滤波部6的滤波参数即陷波频率的推定值。陷波滤波部6逐次采用陷波频率的推定值作为陷波频率。然后，重复s102至s105。
[0159]
在s106中，单位转换部10将自适应更新部7逐次输出的推定值的单位转换为赫兹，并将其作为推定值a输出。
[0160]
在s107中，收敛判定部11基于被转换为赫兹的推定值a，判断推定值a是否收敛，并输出判断为收敛的时刻的收敛推定值。
[0161]
在s108中，自动调整装置12使用收敛推定值对电动机控制系统中包含的控制器2进行自适应调整。
[0162]
根据所述记载的本实施例的技术，提供一种即使是进行固定少数点运算的廉价运算装置，也不依赖于振动分量的振幅的大小、不担心有运算溢出而能够稳定地/高可靠性地逐次更新/推定用于自动调整抑制机械谐振特性的控制器所需的振动分量的频率的推定值的电动机控制装置及其自动调整方法。
[0163]
另外，陷波滤波部6除了数式(1)记载的点阵形式以外，也可以是以下数式所示的直接形式(direct form)。
[0164]
[数式16]
[0165][0166]
其中，ad、rd分别是数式(16)的陷波滤波器的陷波频率及陷波宽度，由自适应更新部7采用al作为ad＝2
×
al。
[0167]
此外，自动调整装置12也可以在振动提取部5的后级具备振动检测部，该振动检测部具有从振动分量yd检测振动的有无，仅在判断为有振动的情况下驱动自动调整装置12的结构。
[0168]
另外，自动调整装置12的输入除了设为输出y以外，也可以设为控制对象机械4的输出m。
[0169]
并且，自动调整装置的输入除了电动机的转速信息以外，也可以是电动机的旋转位置信息。另外，也可以是作为负载而连接的机械装置的转速信息、平移速度信息、旋转位置信息或者平移位置信息。
[0170]
[实施例2]
[0171]
图12表示将实施例2的自动调整装置91应用于一般的电动机的fb控制系统的结构。
[0172]
自动调整装置91构成为，对实施例1所示的自动调整装置12追加更新量调整部92，自适应更新部7被变更为自适应更新部93。
[0173]
在实施例1中，关于al的更新，基于数式(9)并伴有收敛判定部11，由此避免基于σx2的溢出，并且以其他形数式再现σx2带来的标准化处理的优势。
[0174]
然而，关于图6所示的αx的性质带来的al的收敛速度、稳定性涉及的优越性、lpf(λ)带来的al的逐次更新中的变动的平滑度，存在改善的余地。
[0175]
实施例中的自动调整装置91的目的在于改善这些点，对自动调整装置12追加更新量调整部92，以如下那样变更自适应调整部7。
[0176]
《自适应更新部93》
[0177]
[数式17]
[0178]al
(t+1)＝a
l
(t)-μ
p
(t)
·el
(t)
·
xs(t-1)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(17)
[0179]
具体而言，μp仅变更为μp(t)。
[0180]
更新量调整部92基于e(t)以及x(t-1)，逐次算出更新步骤调整系数μp(t)。具体而言，更新量调整部92以μp(t)成为如下那样的方式进行μp(t)的计算。
[0181]
《更新量调整部92》
[0182]
[数式18]
[0183][0184]
将μp(t)＝μm设定为更新步骤的标准的值，通过将es和μs设定为微小，能够通过μs使真值fd周边的更新量微小化。由此，真值周边的al的收敛的稳定性提高，al的逐次更新变得平滑，收敛判定部11容易进行收敛判定。另外，在a远离真值fd的情况下，为μp(t)＝μl＞μm，通过增加更新量，能够加快al的收敛。结果，通过使用更新量调整部92以及自适应更新部93，本实施例的自动调整装置91能够得到加快al的收敛速度、提高真值周边的al的收敛的稳定性这样的与图6所示的标准化处理的优势类似的优势。
[0185]
因此，根据本实施例的技术，提供一种即使是进行固定少数点运算的廉价运算装置，也不依赖于振动分量的振幅的大小、不担心有运算溢出而能够稳定地/高可靠性地逐次更新/推定用于自动调整抑制机械共振特性的控制器所需的振动分量的频率的推定值的电动机控制装置及其自动调整方法。
[0186]
此外，在数式(18)的更新量调整部92中，将μp(t)设为μs、μm、μl3值的变量，但例如也可以以除去μl后得到的2值来实现。另外，也可以进一步分割μm而设为3值以上。无论在哪种情况下，更新量调整部92都能够基于e(t)和x(t-1)，根据|a-fd|的状况来计算μp(t)。
[0187]
[实施例3]
[0188]
实施例3的电动机控制装置设想应用于ac伺服电动机的级联fb控制系统中的速度控制系统。
[0189]
图13表示将图1所示的自动调整装置12应用于ac伺服电动机的级联fb控制系统的电动机控制装置。其中，速度控制器132包含抑制电动机速度(电动机转速)的振动的单元，自动调整装置143应用于速度控制系统以调整速度控制器132。另外，此时的速度控制器132的结构如图2所示。
[0190]
自动调整装置143将根据编码器139的输出由位置/速度产出部141计算出的电动机速度(电动机转速)作为输入来处理。
[0191]
电流控制器133控制电动机的电路部分，在其控制周期比速度控制器132快的前提下，电流控制系统近似地视为1(速度控制器的操作量直达电动机的机械部分(转子))。因此，输入自动调整装置143的输出的速度控制器132的控制对象是与电动机的机械部分(转子)和电动机转子结合的机械142，其相当于图1中的fb控制器的控制对象。
[0192]
在认为机械142的惯性数为1、机械142与电动机转子弹性结合的情况下，控制对象能够视为机械142与电动机转子通过弹簧减震器结合的2惯性系统，控制对象具有包含1组共振/反共振特性的频率特性。
[0193]
另外，在认为机械142的惯性数为2且各惯性通过弹簧减震器结合，其一方与电动机转子弹性结合的情况下，控制对象能够视为各惯性通过弹簧减震器结合的3惯性系统，具有包含2组共振/反共振特性的频率特性。
[0194]
实施例1所示的自动调整装置12不管控制对象的机械142的惯性数如何都能够应
用。也考虑由于控制对象的机械142的惯性数而与位置/速度计算部141检测出的电动机旋转速度重叠的振动分量成为多个的情况，在重叠多个的情况下，也设想自动调整装置12的推定精度变得不良好的情况。但是，即使在作为控制对象的机械142的惯性数多的情况下，也未必全部的惯性对振动产生作出贡献，另外，也不限于由各惯性引起的振动同时产生，振动分量始终重叠的情况，也可以设想个别地产生的情况。在这样的情况下，能够期待通过自动调整装置143进行振动分量的充分推定。
[0195]
因此，在本实施例中，对于ac伺服电动机的级联fb控制系统中的速度控制系统也能够提供如下的电动机控制装置：即使是进行固定少数点运算的廉价的运算装置，也能够不依赖于振动分量的振幅的大小、不担心有运算溢出而稳定地/高可靠性地逐次更新/推定用于自动调整具有抑制机械共振特性的控制器的速度控制器132所需的振动分量的频率的推定值。
[0196]
附图标记的说明
[0197]2…
fb控制器、3
…
电动机、4
…
控制对象机械、5
…
振动提取部、6
…
陷波滤波部、7
…
自适应更新部、8
…
编码部、9
…
限幅部、10
…
单位转换部、11
…
收敛判定部、12
…
自动调整装置、21
…
fb控制器、22
…
控制部、23
…
实际陷波滤波器、31
…
自动调整装置、32
…
高通滤波器、33
…
自适应陷波滤波器、41
…
自适应陷波滤波器、42
…
离散iir型陷波滤波器、43
…
自适应调整部、81
…
收敛判定脉冲计算部、91
…
自动调整装置、92
…
更新量调整部、93
…
自适应更新部、132
…
速度控制器、133
…
电流控制器、135
…
pwm、136
…
逆变器、137
…
ac伺服电动机、138
…
电流检测传感器、139
…
编码器、141
…
位置/速度计算部、142
…
控制对象的机械、143
…
自动调整装置。