一种基于离散全阶观测器的感应电机转速观测方法

本发明属于电机控制技术领域，具体涉及一种基于离散全阶观测器的感应电机转速观测方法。

背景技术：

无速度传感器感应电机矢量控制技术具有高可靠性、结构简单、成本低廉等优点，广泛应用于石油钻机、矿车、数控切割机等各种工业场合。现如今，已有多种感应电机转速观测方法被提出，如：模型参考自适应系统、滑模观测器、自适应全阶观测器等。其中自适应全阶观测器通过合适的自适应率，利用测量的定子电流与其估计值之间的误差对估测变量进行校正。全阶观测器具有较强的参数鲁棒性，合理选择速度自适应律和观测器增益，可以使无速度传感器控制系统达到与配备速度传感器的控制系统类似的性能。

通常，全阶观测器在连续域中设计，但在基于工业微处理器的系统中，模型需进行离散化处理，而前向欧拉法因其方法简单而被作为最常用的离散方法。然而离散化必然会带来离散化误差，导致观测器性能恶化甚至不稳定。尤其在大功率或超高速驱动器中，为减小逆变器开关损耗，常常会让逆变器开关频率与电机运行频率之比减小，即降低载波比，此时基于前向欧拉法的全阶观测器模型的离散误差会随着载波比的减小急剧增大，导致观测器严重的震荡甚至不稳定。针对此问题，后向欧拉法和双线性法虽可提高观测器的估计精度和稳定性，但是其高计算量和隐式特性增加了系统的复杂性，所以寻求一种感应电机离散全阶观测器稳定性与精度提升策略对整个无速度传感器矢量控制系统的性能提升具有重要意义。

技术实现要素：

本发明的目的是为解决在降低载波比的情况下，现有的无速度传感器感应电机离散全阶观测器的稳定性与观测精度差的问题，而提出了一种基于离散全阶观测器的感应电机转速观测方法。

本发明为解决上述技术问题所采取的技术方案是：一种基于离散全阶观测器的感应电机转速观测方法，所述方法具体包括以下步骤：

步骤一、将电机定子电流与转子磁链作为状态变量，建立感应电机数学模型；

基于建立的感应电机数学模型，推导出连续域全阶观测器的数学模型，并根据连续域全阶观测器数学模型计算当前采样周期起点时状态变量的一阶导数k(k)；

步骤二、根据当前采样周期起点时的状态变量观测值和步骤一计算得到的k(k)估计当前采样周期中点时状态变量观测值，并根据当前采样周期中点时状态变量观测值和步骤一的连续域全阶观测器数学模型计算当前采样周期中点时状态变量的一阶导数k′(k)；

步骤三、根据当前采样周期起点时的状态变量观测值和步骤二计算得到的k′(k)重新估计当前采样周期中点时状态变量观测值，并根据重新估计出的当前采样周期中点时状态变量观测值和步骤一的连续域全阶观测器数学模型重新计算当前采样周期中点时状态变量的一阶导数k″(k)；

步骤四、根据当前采样周期起点时的状态变量观测值和步骤三计算得到的k″(k)估计当前采样周期终点时状态变量观测值，并根据当前采样周期终点时状态变量观测值和步骤一的连续域全阶观测器数学模型计算当前采样周期终点时状态变量的一阶导数k″′(k)；

步骤五、根据步骤一至步骤四计算得到的k(k)、k′(k)、k″(k)以及k″′(k)，计算k(k)、k′(k)、k″(k)和k″′(k)的加权平均数，根据计算出的加权平均数、当前采样周期起点时的状态变量观测值与采样周期长度，最终估计出下一个采样周期的状态变量观测值；

步骤六、根据估计出的下一个采样周期的状态变量观测值和采集的实际定子电流矢量，计算出在下一个采样周期感应电机的转速。

本发明的有益效果是：本发明提出了一种基于离散全阶观测器的感应电机转速观测方法，本发明首先建立全阶观测器连续域模型，其次基于全阶观测器连续域模型，分别预测一个采样周期区间内四个状态变量点的导数，并取四者的加权平均数；最后，根据当前状态变量值、加权平均数与采样周期长度ts，估计得到下一个采样周期时状态变量值。本发明所设计的离散全阶观测器，即使在低开关频率(500hz-1500hz)时也能准确观测转速，当ts＝1/1200s时，基于本发明所提方法的最大离散误差小于2％，在保持较低计算量的同时，实现了无速度传感器感应电机驱动系统在极低载波比下的高稳定高精度运行。

附图说明

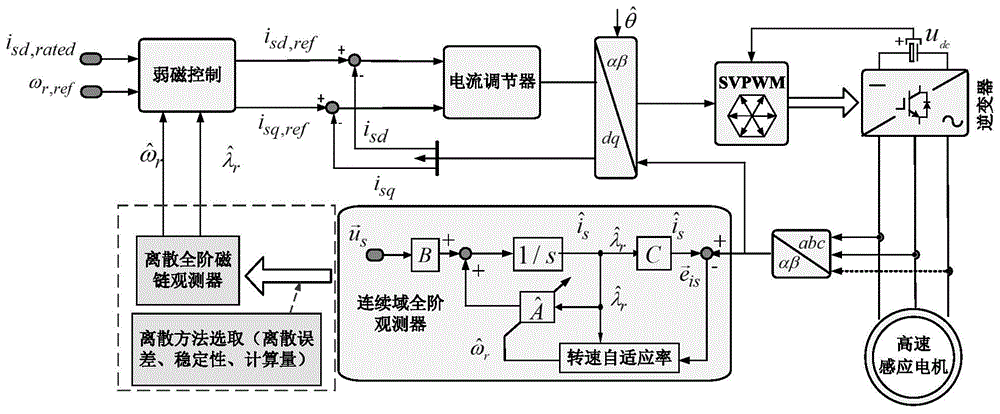
图1为本发明基于全阶观测器的无速度传感器感应电机矢量控制系统框图；

图中，ωr,ref为系统给定转速，为全阶观测器观测转速，为全阶观测器观测磁链，isd,rated为励磁电流给定值，isd,ref为弱磁分配的给定d轴电流分量，isq,ref为弱磁分配的给定q轴电流分量，isd为检测到的定子电流d轴分量，isq为检测到的定子电流q轴分量，为坐标变换旋转角，αβ为两相静止坐标系，dq为两相旋转坐标系，svpwm为电压空间矢量控制，udc为直流电压，abc为三相坐标系，为定子电流矢量，为定子电流误差矢量，为定子电压矢量；

图2a为ts＝1/1200s时基于前向欧拉法的离散全阶观测器极点分布情况的示意图；

图2b为ts＝1/600s时基于前向欧拉法的离散全阶观测器极点分布情况的示意图；

图3a为ts＝1/1200s时基于预估校正法的离散全阶观测器极点分布情况的示意图；

图3b为ts＝1/600s时基于预估校正法的离散全阶观测器极点分布情况的示意图；

图4a为ts＝1/1200s时基于本发明所提出策略的离散全阶观测器极点分布情况的示意图；

图4b为ts＝1/600s时基于本发明所提出策略的离散全阶观测器极点分布情况的示意图；

图5为本发明所提出的离散全阶观测器与基于前向欧拉法和预估校正方法的离散全阶观测器的离散误差的对比分析图；

图6a为转速频率30hz，空载下基于前向欧拉法的离散全阶观测器的定子电流α轴分量波形图；

图6b为转速频率30hz，空载下基于预估校正法的离散全阶观测器的定子电流α轴分量波形图；

图6c为转速频率30hz，空载下本发明所提出的离散全阶观测器的定子电流α轴分量波形图；

图7a为转速频率30hz，额定负载下基于前向欧拉法的离散全阶观测器的定子电流α轴分量波形图；

图7b为转速频率30hz，额定负载下基于预估校正法的离散全阶观测器的定子电流α轴分量波形图；

图7c为转速频率30hz，额定负载下本发明所提出的离散全阶观测器的定子电流α轴分量波形图；

图8a为转速频率120hz，空载下基于预估校正法的离散全阶观测器的定子电流α轴分量波形图；

图8b为转速频率120hz，本发明所提出的离散全阶观测器的定子电流α轴分量波形图；

图9a为转速频率120hz，轻载(4n·m)下基于预估校正法的离散全阶观测器的定子电流α轴分量波形图；

图9b为转速频率120hz，轻载(4n·m)下本发明所提出的离散全阶观测器的定子电流α轴分量波形图。

具体实施方式

具体实施方式一、结合图1说明本实施方式。本实施方式所述的一种基于离散全阶观测器的感应电机转速观测方法，所述方法具体包括以下步骤：

步骤一、将电机定子电流与转子磁链作为状态变量，建立感应电机数学模型；

基于建立的感应电机数学模型，推导出连续域全阶观测器的数学模型，并根据连续域全阶观测器数学模型计算当前采样周期起点时状态变量的一阶导数k(k)；

步骤二、根据当前采样周期起点时的状态变量观测值和步骤一计算得到的k(k)估计当前采样周期中点时状态变量观测值，并根据当前采样周期中点时状态变量观测值和步骤一的连续域全阶观测器数学模型计算当前采样周期中点时状态变量的一阶导数k′(k)；

步骤三、根据当前采样周期起点时的状态变量观测值和步骤二计算得到的k′(k)重新估计当前采样周期中点时状态变量观测值，并根据重新估计出的当前采样周期中点时状态变量观测值和步骤一的连续域全阶观测器数学模型重新计算当前采样周期中点时状态变量的一阶导数k″(k)；

步骤四、根据当前采样周期起点时的状态变量观测值和步骤三计算得到的k″(k)估计当前采样周期终点时状态变量观测值，并根据当前采样周期终点时状态变量观测值和步骤一的连续域全阶观测器数学模型计算当前采样周期终点时状态变量的一阶导数k″′(k)；

步骤五、根据步骤一至步骤四计算得到的k(k)、k′(k)、k″(k)以及k″′(k)，计算k(k)、k′(k)、k″(k)和k″′(k)的加权平均数，根据计算出的加权平均数、当前采样周期起点时的状态变量观测值与采样周期长度，最终估计出下一个采样周期的状态变量观测值；

步骤六、根据估计出的下一个采样周期的状态变量观测值和采集的实际定子电流矢量，观测出在下一个采样周期感应电机的转速。

具体实施方式二：本实施方式与具体实施方式一不同的是，所述步骤一中，将电机定子电流与转子磁链作为状态变量，建立感应电机数学模型；其具体过程为：

式中：定子电流矢量isα是在两相坐标系下的定子α轴分量，isβ是在两相坐标系下的定子β轴分量，转子磁链矢量λrα是在两相坐标系下的定子α轴分量，λrβ是在两相坐标系下的定子β轴分量，输入电压矢量u＝[usαusβ]^t，usα是u在两相坐标系下的定子α轴分量，usβ是u在两相坐标系下的定子β轴分量，a为系统矩阵，a11、a12、a21、a22为系统矩阵系数，x为状态变量矩阵，为当前采样周期的定子电流矢量，为当前采样周期的转子磁链矢量，b为输入矩阵，b为电压项系数，t为时间变量。

具体实施方式三：本实施方式与具体实施方式二不同的是，所述系统矩阵系数a11、a12、a21、a22的表达式为：

a11＝a′11i

a12＝a′121i+a′122j

a21＝a′21i

a22＝a′221i+ωrj

其中，σ是漏感系数，rs是定子电阻，rr是转子电阻，ls是定子电感，lm是互感，lr是转子电感，ωr是电角度转子转速，i为实部矩阵，j为虚部矩阵。

具体实施方式四：本实施方式与具体实施方式三不同的是，所述电压项系数b的表达式为：

b＝b′i

其中：

具体实施方式五：本实施方式与具体实施方式四不同的是，所述基于建立的感应电机数学模型，推导出连续域全阶观测器的数学模型；其具体过程为：

其中：“^”代表观测值，为a的观测值，为a11的观测值，为a12的观测值，为a21的观测值，为a22的观测值，为的观测值，为的观测值，为x的观测值。

由式(1)减去式(2)，可以得状态误差方程如下：

式中：

根据李雅普诺夫稳定性理论，推导转速自适应律为：

其中，kp为比例系数，ki为积分系数，s为拉普拉斯算子。

具体实施方式六：本实施方式与具体实施方式五不同的是，所述根据连续域全阶观测器数学模型(公式(2))计算当前采样周期起点时状态变量的一阶导数k(k)；其具体过程为：

其中：代表当前采样周期起点状态变量观测值，u(k)代表当前采样周期输入电压；

将公式(5)展开为：

其中：“ksα(k)”代表当前采样周期起点时两相坐标系下定子电流α轴分量的一阶导数，“ksβ(k)”代表当前采样周期起点时两相坐标系下定子电流β轴分量的一阶导数，“krα(k)”代表当前采样周期起点时两相坐标系下转子磁链α轴分量的一阶导数，“krβ(k)”代表当前采样周期起点时两相坐标系下转子磁链β轴分量的一阶导数，代表当前采样周期定子电流α轴分量观测值，代表当前采样周期定子电流β轴分量观测值，代表当前采样周期转子磁链α轴分量观测值，代表当前采样周期转子磁链β轴分量观测值，uα(k)代表当前采样周期定子电压α轴分量，uβ(k)代表当前采样周期定子电压β轴分量。

具体实施方式七：本实施方式与具体实施方式六不同的是，所述步骤二的具体过程为：

其中：代表当前采样周期中点状态变量观测值，ts代表采样周期长度；

将公式(7)和公式(8)联立得：

将公式(9)展开为：

其中：“k′sα(k)”代表当前采样周期中点时两相坐标系下定子电流α轴分量的一阶导数，“k′sβ(k)”代表当前采样周期中点时两相坐标系下定子电流β轴分量的一阶导数，“k′rα(k)”代表当前采样周期中点时两相坐标系下转子磁链α轴分量的一阶导数，“k′rβ(k)”代表当前采样周期中点时两相坐标系下转子磁链β轴分量的一阶导数。

具体实施方式八：本实施方式与具体实施方式七不同的是，所述步骤三的具体过程为：

其中：代表重新估计出的当前采样周期中点状态变量观测值；

将公式(11)和公式(12)联立得：

将公式(13)展开为：

其中：“k″sα(k)”代表重新估计出的当前采样周期中点时两相坐标系下定子电流α轴分量一阶导数，“k″sβ(k)”代表重新估计出的当前采样周期中点时两相坐标系下定子电流β轴分量一阶导数，“k″rα(k)”代表重新估计出的当前采样周期中点时两相坐标系下转子磁链α轴分量一阶导数，“k″rβ(k)”代表重新估计出的当前采样周期中点时两相坐标系下转子磁链β轴分量一阶导数。

具体实施方式九：本实施方式与具体实施方式八不同的是，所述步骤四的具体过程为：

其中：代表当前采样周期终点状态变量观测值，u(k+1)代表下一采样周期输入电压；

将公式(15)和公式(16)联立得：

将公式(17)展开为：

其中：uα(k+1)代表下一采样周期定子电压α轴分量，uβ(k+1)代表下一采样周期定子电压β轴分量，“k″′sα(k)”代表当前采样周期终点时两相坐标系下定子电流α轴分量的一阶导数，“k″′sβ(k)”代表当前采样周期终点时两相坐标系下定子电流β轴分量的一阶导数，“k″′rα(k)”代表当前采样周期终点时两相坐标系下转子磁链α轴分量的一阶导数，“k″′rβ(k)”代表当前采样周期终点时两相坐标系下转子磁链β轴分量的一阶导数。

具体实施方式十：本实施方式与具体实施方式九不同的是，所述步骤五的具体过程为：

其中：k为加权平均数，代表下一采样周期状态变量观测值，ts为采样周期长度；

将公式(19)和公式(20)联立得：

将公式(21)展开为：

其中：代表下一采样周期定子电流α轴分量观测值，代表下一采样周期定子电流β轴分量观测值，代表下一采样周期转子磁链α轴分量观测值，代表下一采样周期转子磁链β轴分量观测值。

采用以下实施例验证本发明的有益效果：

为进一步提升低载波比时离散全阶观测器的稳定性与精度，本发明首先分析离散全阶观测器极点分布情况对离散全阶观测器的稳定性进行分析。为保证离散全阶观测器是稳定的，观测器的所有极点必须位于单位圆内。图2a和图2b为基于前向欧拉法的离散全阶观测器极点分布情况；图3a和图3b为基于预估校正法的离散全阶观测器极点分布情况；图4为本发明的离散全阶观测器极点分布情况。

由图2a可知，对于基于前向欧拉法的离散全阶观测器，在ts＝1/1200s时，离散全阶观测器的临界稳定点为ωr＝70hz，此时载波比为17。由图2b可知，在ts＝1/600s时，离散全阶观测器的临界稳定点为ωr＝50hz，此时载波比为12。因此在低载波比时，采用前向欧拉法的离散全阶观测器不能在全速范围内(0-200hz)稳定运行。由图3a可知，对于预估校正法的离散全阶观测器，在ts＝1/1200s时，离散全阶观测器的临界稳定点为ωr＝180hz，此时载波比为6.7。由图3b可知，在ts＝1/600s时，离散全阶观测器的临界稳定点为ωr＝110hz，此时载波比为5.1。因此在低载波比时，采用预估校正方法的离散全阶观测器不能在全速范围内(0-200hz)稳定运行。

本发明的离散全阶观测器极点分布情况如图4a和图4b所示，由图中可以看出，所有极点均在单位圆内，即使在载波比为3时，本发明所提的离散全阶观测器也能在全速范围内稳定运行。

本发明采用矩阵的2-范数对全阶观测器近似离散模型与精确离散模型的误差进行定量分析。矩阵的2-范数定义为：

式中：a∈r^n×n，λmax(a^ta)为a^ta的最大特征值。

根据公式(2)，可以看到全阶观测器模型为一阶常微分方程，计算机通常用数值方法对微分方程求解，即通过某种离散方法，将微分方程转换差分方程后对其求解。定义ts为离散步长，基于非齐次矩阵的矩阵方程定理，可得离散全阶观测器的精确离散形式为：

可以看到其状态转移矩阵与输入矩阵均由矩阵指数函数构成，对矩阵指数函数进行麦克劳林级数展开：

各种离散方法实际上是对精确离散模型中的矩阵指数函数进行近似处理，因此离散全阶观测器的离散精度由对矩阵指数函数的离散化近似精度决定，因此选取矩阵2-范数为：

其中：φ为离散全阶观测器的状态转移矩阵。

根据离散观测器数学模型，经过数学推导，可得基于前向欧拉法的离散全阶观测器的状态转移矩阵为：

φ1＝1+ats(27)

基于预估校正法的离散全阶观测器的状态转移矩阵为：

本发明所提出的离散全阶观测器的状态转移矩阵为：

分别将公式(27)、(28)、(29)的状态转移矩阵φ1、φ2、φ3带入到公式(24)的φ中，得到如图5所示的基于本发明所提出策略的离散全阶观测器与基于前向欧拉法和预估校正方法的离散全阶观测器的离散误差的对比分析。水平轴代表着转子转速频率，单位为hz,垂直轴用百分比表示离散误差。从图5中可以看出，随着转速的增大，三种离散方法的离散误差随着转子转速的上升和离散步长的增加而增大。但是，可以明显看出，相较于基于前向欧拉法和预估校正法的离散全阶观测器，本发明所提出的离散全阶观测器的离散误差要低的多。当ts＝1/1200s时，基于本发明所提方法近似的离散全阶观测器的最大误差小于2％，而基于前向欧拉法和预估校正法的离散全阶观测器的最大误差分别在20％和60％以下。即使在ts＝1/600s的情况下，基于本发明所提出策略的离散全阶观测器在150hz时的误差也在10％内，远小于基于前向欧拉法和预估校正法的离散观测器。

实验部分：

在开关频率为600hz，不同电机转速、负载情况下，分析在采用不同离散全阶观测器时相应的定子电流α轴分量的实验波形及其估计值。图6a为转速频率30hz，空载下基于前向欧拉法的离散全阶观测器的定子电流α轴分量波形；图6b为转速频率30hz，空载下基于预估校正法的离散全阶观测器的定子电流α轴分量波形；图6c为转速频率30hz，空载下本发明所提出的离散全阶观测器的定子电流α轴分量波形。图7a为转速频率30hz，额定负载下基于前向欧拉法的离散全阶观测器的定子电流α轴分量波形；图7b为转速频率30hz，额定负载下基于预估校正法的离散全阶观测器的定子电流α轴分量波形；图7c为转速频率30hz，额定负载下本发明所提出的离散全阶观测器的定子电流α轴分量波形。

在开关频率600hz，给定转速频率30hz时，由图6a、图6b、图6c、图7a、图7b和图7c可以看到，基于前向欧拉法的离散全阶观测器对定子电流估计值的幅值与相位均有很大误差，且空载时估计误差较负载时大，离散观测器精度差，此时感应电机在无速度传感器模式下已无法高精度运行。但是基于预估校正法和本发明所提出的离散全阶观测器对定子电流仍估计精确，离散观测器精度良好。

图8a为转速频率120hz，空载下基于预估校正法的离散全阶观测器的定子电流α轴分量波形；图8b为转速频率120hz，本发明所提出的离散全阶观测器的定子电流α轴分量波形。图9a为转速频率120hz，轻载(4n·m)下基于预估校正法的离散全阶观测器的定子电流α轴分量波形；图9b为转速频率120hz，轻载(4n·m)下本发明所提出的离散全阶观测器的定子电流α轴分量波形。

在开关频率600hz，给定转速频率120hz时，由图8a、图8b、图9a和图9b可以看到，无论是否带载，随着转速的升高，基于预估校正法法的离散全阶观测器对定子电流估计值的幅值误差与相位误差逐渐增大，空载时估计误差较大，离散观测器精度差，此时感应电机在无速度传感器模式下已无法高精度运行。但是本发明所提出的离散全阶观测器对定子电流仍估计精确，实现了无传感器感应电机驱动系统在低载波比下的高精度运行。

以上对所提出的一种感应电机离散全阶观测器稳定性与精度提升策略进行了详细介绍，以上实例介绍仅用帮助理解本发明的具体方法及核心思想；对于相关领域的一般技术人员，依照本发明的思想，在上述说明的基础上还可做出其他改变，这里无法对所有方法逐一例举，凡是依照本发明所进行的明显改变和变形都属于本发明所附的权利要求的保护范围。