一种直流电网拓扑对故障电流影响的评估方法

1.本发明涉及直流电网拓扑与故障电流评估技术领域，具体为一种直流电网拓扑对故障电流影响的评估方法。


背景技术：

2.多端柔性直流电网以其低谐波、可靠性高、易于扩展等优势成为当今研究的热点。实际工程中，单极接地故障事件发生频率最高。真双极系统发生单极接地故障后，子模块迅速放电，并向故障点注入大量浪涌电流，换流站出口电压极速下降，桥臂电流及线路电流急剧上升，严重威胁电网的安全稳定运行。因此，研究拓扑结构对单极故障电流的影响机理及拓扑参数对故障电流的影响对电网规划研究具有重要意义。
3.当前，对柔性直流输电故障电流的研究主要有三种方法，即微分方程法、状态空间方程法和高频等效模型法。
4.最常见和经典的方法是微分方程法，即建立原始故障电路的微分方程，从而获得时域表达式以进行分析。但是，时域表达式过于复杂，难以对拓扑对故障电流的影响机制进行研究。状态空间方程法是将换流站简化为rlc电路，从而可以通过状态空间方程计算出线路故障电流。但状态空间方法通过求解高阶微分方程来计算故障电流，只能求得时域数值结果而无法获得故障电流的显式表达式，从而难以分析拓扑对故障电流的影响。另一方面，现有的高频等效模型仅针对两端直流输电系统，不适用于直流电网拓扑研究，更难以应用于直流电网拓扑对故障电流影响的研究中。因此，探究拓扑对故障电流的影响及寻求拓扑对故障电流影响的评估指标具有重要意义。
5.具体的，如现有技术1建立多端真双极系统等效电路，[参考文献：y.li,j.li,l.xiong,x.zhang and z.xu,“dc fault detection in meshed mtdc systems based on transient average value of current,”ieee trans.ind.electron.,vol.67,no.3,pp.1932
‑
1943,mar.2020.]，其缺点是仅针对双端换流站直流输电系统，不适用于拓扑研究。
[0006]
如现有技术2状态空间方程计算故障电流方法[参考文献1:c.li,c.zhao,j.xu,y.ji,f.zhang and t.an,“a pole
‑
to
‑
pole short
‑
circuit fault current calculation method for dc grids,”ieee trans.power syst.,vol.32,no.6,pp.4943
‑
4953,nov.2017；参考文献2:汤兰西,董新洲.mmc直流输电网线路短路故障电流的近似计算方法[j].中国电机工程学报,2019,39(02):490
‑
498+646.]，其缺点是只能求得时域数值结果而无法获得故障电流的显式表达式，从而难以分析故障电流的影响因素。
[0007]
现有技术3分析了金属回线接地方式下单极故障各特征量变化情况，[参考文献：朱韬析,候元文,王超,陈为化.直流输电系统单极金属回线运行方式下线路接地故障及保护研究[j].电力系统保护与控制,2009,37(20):133
‑
138]其缺点未深入探讨拓扑结构及拓扑参数对故障电流影响，没有提出可以评估拓扑对故障电流影响的指标。


技术实现要素：

[0008]
针对上述问题，本发明的目的在于提供一种直流电网拓扑对故障电流影响的评估方法，通过评估直流电网拓扑对故障电流影响的指标k，确定直流电网故障电流初期主要来自于哪些换流站，能够避免繁琐的计算，直接、快速地评估拓扑对故障电流的影响。技术方案如下：
[0009]
一种直流电网拓扑对故障电流影响的评估方法，包括以下步骤：
[0010]
步骤1：建立用于极地故障分析的mmc和故障直流线路的解耦等效模型
[0011]
将电路等效为解耦的稳态电路和故障电路，对应的将故障电流分为两个分量：稳态分量i0和故障分量i
f
；稳态分量i0由潮流结果获得，由电路参数和控制策略决定；故障分量i
f
通过频域中的故障电路来计算，计算故障分量i
f
时，考虑电感器和电容器的瞬态动态，通过频域中的故障电路来计算；在等效电路中，
[0012][0013]
z0＝r0+(sl0+sl
d
)
[0014]
其中，r
eq
、l
eq
和c
eq
为换流站到与金属回线联结点之间的等效电阻、电感和电容，z0是等效线路阻抗；l
n
为中性线电抗，l
d
为直流电抗器的电感，r0和l0分别为直流线电阻和电感，r
m
和l
m
分别是臂电阻和臂电感；c
m
为mmc换流站单个子模块等效电容；n为单个桥臂子模块数量；s为复频率；
[0015]
步骤2：建立金属回线接地方式下解耦等效电路模型
[0016]
若直流电网为大地回线接地，则其解耦等效模型中各换流站与接地点为独立支路，而当直流电网为金属回线接地时，其解耦等效模型中接地层拓扑复杂，需要解耦以得到与大地回路类似的等效电路模型；
[0017]
将金属回线层解耦等效为各个换流站阻抗增加，将接地电感l
g
和接地电阻r
g
按各个转移阻抗成比例分配到各个换流站支路，使等效电路平面化；
[0018]
在金属回线接地层平面网格中，计算节点i和j之间的实际电感l
ij
，以及从节点i到j的转移电感l
′
ij
，其中，节点i、j表示换流站与金属回线层联结点编号；
[0019]
计算换流站i站出口处到公共接地点的总转移电感值l
if
，然后计算接地电感l
g
分配到换流站i站到的比例h
i
；
[0020]
则将金属回线解耦后换流站i站到接地点的等效电感值l
ieq
为：
[0021][0022]
步骤3：提出拓扑对故障电流影响的评估指标k
[0023]
同一直流电网中，各换流站的等效电感近似相等，因此，n个换流站并联的总等效电感等于任意一个换流站等效电感的1/n倍，即
[0024][0025]
其中，l
′
neq
为总等效电感；
[0026]
通过计算与对比连接不同数量换流站的等效总阻抗，即可明确影响故障电流的主要换流站。因此，提出拓扑对故障电流影响的评估指标为
[0027][0028]
其中，l
line
为换流站之间线路的等效电感；
[0029]
通过上式可计算k值不同时含不同数量换流站的总等效电感。设置评估指标k的临界值，当评估指标k小于临界值时，仅考虑近端换流站和次近端换流站的等效电感与考虑全拓扑(含所有换流站)电感几乎相等，则认为初期故障电流仅由近端换流站和次近端换流站影响；而当评估指标k大于临界值时，仅考虑近端换流站和次近端换流站的等效电感无法代表所有换流站的特性，因此认为所有换流站都会影响初期故障电流；所述近端换流站为与故障线路直接相连的换流站，所述次近端换流站为与近端换流站通过非故障线路连接的换流站。
[0030]
进一步的，所述步骤2中，电网为4端电网且第2端接地时，计算接地电感l
g
分配到换流站i站到的比例h
i
的方法为：
[0031]
从节点1到节点2的转移电感l
′
12
、从节点3到节点2的转移电感l
′
32
、从节点4到节点2的转移电感l
′
42
分别表示为：
[0032]
l
′
12
＝(l
12
)//(l
14
+l
23
+l
34
)
[0033]
l
′
32
＝(l
23
)//(l
14
+l
12
+l
34
)
[0034]
l
′
42
＝(l
12
+l
14
)//(l
23
+l
34
)
[0035]
将公共接地点解耦到独立等效接地点，则等效总转移电感值表示为：
[0036][0037][0038][0039][0040]
其中，l
if
为换流站i站出口处到公共接地点的总转移电感值，i＝1,2,3,4；
[0041]
令h
i
为
[0042][0043]
本发明的有益效果是：本发明明确了拓扑对故障电流影响的评估指标k，评估指标决定了直流电网拓扑对单极接地短路初期故障电流的影响，也即故障初期电流主要由哪些换流站参与放电。根据指标k研究表明，大地回路和金属回路直流电网的影响机制不同，在大地回路直流电网中，故障电流主要受相邻和次相邻换流站的影响，在金属回路直流电网中，所有换流站对故障电流的贡献均不可忽略。提出的拓扑对故障电流影响的评估指标k，可以直接、快速地评估拓扑对故障电流的影响，有利于工程实践。
附图说明
[0044]
图1为大地回路的基于双极mmc的直流电网：(a)大地回路的典型四端直流电网，(b)双极mmc和具有极对地故障的直流线路，(c)正极mmc和直流线路的极点对地故障。
[0045]
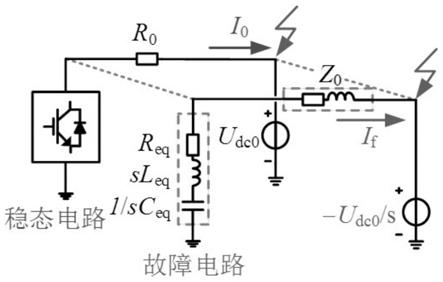
图2为用于极地故障分析的mmc和故障直流线路的解耦等效模型。
[0046]
图3为金属回线解耦模型。
[0047]
图4为直流电网金属回路等效模型：(a)解耦前(b)解耦后。
[0048]
图5为公共接地点去耦前后直流电网模型。
[0049]
图6为链式直流电网示意图。
[0050]
图7为大地回线下不同数量换流站直流电网的等效总阻抗。
[0051]
图8为金属回线下不同数量换流站直流电网的等效总阻抗。
[0052]
图9为不同k值时，zc2和zc4的幅值差图。
[0053]
图10(a)为链式直流电网示意图。
[0054]
图10(b)直流环网示意图。
[0055]
图11为链式直流电网大地回线下不同换流站数量放电示意图。
[0056]
图12为链式直流电网金属回线下不同换流站数量放电示意图。
[0057]
图13为直流环网大地回线下各换流站出口电压示意图。
[0058]
图14为直流环网金属回线下各换流站出口电压示意图。
具体实施方式
[0059]
下面结合附图和具体实施例对本发明做进一步详细说明。
[0060]
1.建立多端系统高频等效模型
[0061]
带接地回路的基于双极mmc的直流电网如图1所示，其中l
n
为中性线电抗，l
d
为直流电抗器的电感，r0和l0分别为直流线电阻和电感，r
m
和l
m
分别是臂电阻和臂电感。
[0062]
基于接地回路的接地方案的配置如图1(a)所示。图1(b)显示了典型的基于双极mmc的直流电网，具有极地故障，其中该站配置有接地回路以用于非对称操作。带接地回路的直流电网在每个换流站的正极和负极之间的中点有一个理想的接地点，所有换流站在接地点处等电位。以正极为重点来说明建模和分析。正极mmc的配置，即mmcp，如图1(c)所示。
[0063]
如图2所示，故障电流由两个分量组成，即稳态分量和故障分量(分别如图2中的i0和i
f
)，可以通过稳态和故障电路计算。更具体地说，故障电流的稳态分量是由潮流结果获得的，它由电路参数和控制策略决定。在计算故障电流的故障分量时，应考虑电感器和电容器的瞬态动态。为此，故障分量可以通过频域中的故障电路来计算(即高频等效模型)，如图2所示，其中u
dc0
是稳态直流电压，电压源
‑
u
dc0
/s，表示馈入的瞬时阶跃信号故障时刻的故障点。r
eq
、l
eq
和c
eq
分别是mmc和dc线路的等效电阻、电感和电容，z0是等效线路阻抗，其计算方式为
[0064][0065]
z0＝r0+(sl0+sl
d
)
ꢀꢀꢀ
(2)
[0066]
其中，l
n
为中性线电抗，l
d
为直流电抗器的电感，r0和l0分别为直流线电阻和电感，r
m
和l
m
分别是臂电阻和臂电感；c
m
为mmc换流站单个子模块等效电容；n为单个桥臂子模块数
量；s为复频率。
[0067]
2.提出金属回线接地方式下解耦等效电路模型
[0068]
金属回线接地方式下考虑全拓扑参数，将金属回线层解耦等效为各个换流站阻抗增加，解耦后与大地回线等效电路模型相似，计算方式相同，此处不再赘述。金属回线具体解耦图如图3。
[0069]
图3的解耦思想相当于将接地电感l
g
和接地电阻r
g
按各个转移阻抗成比例分配到各个换流站支路，见下文具体推导。
[0070]
以4端电网且第2端接地为例，图4表示金属回线接地层四节点平面网格，对应于图3中(b)到(c)的变换。l
ij
表示节点i和j之间的实际电感，l
′
nm
表示从节点n到m的转移电感，其中，节点i、j、n、m表示换流站与金属回线层联结点编号。
[0071]
则从节点1到节点2的转移电感l
′
12
、从节点3到节点2的转移电感l
′
32
、从节点4到节点2的转移电感l
′
42
分别表示为：
[0072]
l
′
12
＝(l
12
)//(l
14
+l
23
+l
34
)
ꢀꢀꢀ
(3)
[0073]
l
′
32
＝(l
23
)//(l
14
+l
12
+l
34
)
ꢀꢀꢀ
(4)
[0074]
l
′
42
＝(l
12
+l
14
)//(l
23
+l
34
)
ꢀꢀꢀ
(5)
[0075]
将公共接地点解耦到独立等效接地点可以如图5所示。
[0076]
如图5所示。等效总转移电感值可表示为
[0077][0078][0079][0080][0081]
其中，l
if
为换流站i站出口处到公共接地点的总转移电感值，i＝1,2,3,4。
[0082]
令h
i
为
[0083][0084]
则
[0085][0086]
其中，l
ieq
表示将金属回线解耦后换流站i站到接地点的等效电感值，h
i
表示接地电感l
g
分配到换流站i站到的比例；l
′
ij
为节点i和j间的转移电感。
[0087]
3.提出拓扑对故障电流影响的简化指标k
[0088]
定义，与故障线路直接相连的换流站成为近端换流站，与近端换流站通过非故障线路连接的换流站称为次近端换流站，其他换流站称为远端换流站。以一个如图6所示的链式直流电流电网为例(其他拓扑形状或其他端数的直流电网中也适用)，计算连接不同数量换流站的等效总阻抗，结果如图7和图8所示。根据工程典型参数(张北模型典型参数)可知，
采用大地回线时近端次近端阻抗等效阻抗(z
c2
)与全拓扑阻抗(z
c4
)接近，而采用金属回线下则需考虑全拓扑换流站阻抗。
[0089]
虽然故障电流可以基于状态空间模型进行解析计算，但该计算需要繁重的计算，当换流站数量增加时，这可能会花费大量时间。因此，研究电网拓扑对故障电流水平的影响，即直流电网的最大故障电流值，既不具有成本效益，也不具有计算效率。为了解决这个问题，需要一种能够以简单快速的方式评估不同直流电网拓扑的故障电流影响的简化指标。同一直流电网中，各换流站的等效电感近似相等，因此，n个换流站并联的总等效电感等于任意一个换流站等效电感的1/n倍，即
[0090][0091]
其中，l
′
neq
为总等效电感；
[0092]
令
[0093][0094]
其中，l
line
为换流站之间线路的等效电感。
[0095]
得到
[0096][0097]
通过上式可计算k值不同时含不同数量换流站的总等效电感。
[0098]
图9表示不同k值时，仅考虑近端、次近端换流站等效阻抗与考虑全拓扑等效阻抗差。由图9可知，不同k值下，忽略远端换流站的误差不同。k越大，忽略远端换流站的误差越大。通过金属回线解耦理论可知，等效于l
eq
增加，k增大，故远端换流站不可忽略。其他参数换流站参数及类型可具体参照图9。
[0099]
为判断直流电网拓扑对单极接地短路故障电流的影响，设置k临界值，当k小于临界值时，认为初期故障电流仅由近端换流站和次近端换流站影响，而当k大于临界值时，认为所有换流站都会影响初期故障电流初期。用于判断直流电网拓扑对故障电流影响的k临界值需要根据工程需要进行设置，如工程对故障电流分析准确性要求较高，则k临界值可设置得较小，使得在故障电流分析时将等效阻抗间的误差考虑得更细致；反之，如工程对故障电流分析准确性要求不太高，而更追求故障电流水平的快速评估，则可将k临界值设置得较大。
[0100]
能够利用指标k判断直流电网单极接地初期故障电流由哪些换流站影响。基于指标k可得出结论，当直流电网采用大地回线且采用典型参数时，在故障电流初期，仅近端，次近端换流站放电；当直流电网采用金属回线且采用典型参数时，在故障电流初期，包括近端、次近端和远端换流站均放电。
[0101]
实施例：
[0102]
为了验证提出的关于电网拓扑对故障电流特性影响的机制，在pscad软件中测试了两个算例：
[0103]
实施例1：一个链式直流电网，如图10(a)所示。应该提到的是，图10(a)是链式直流电网的示意图，显示换流站的连接。因此，没有出现直流线路。线路参数，其中换流站的配置
如表1所示。
[0104]
实施例2：为进一步验证该理论，在五端网格直流电网中进行了案例研究，直流环网示意图如图10(b)所示，其中换流站的配置如表1所示。极对地故障发生在连接换流站1和5的线路上。
[0105]
表1实施例系统参数
[0106][0107]
验证方案1：拓扑影响机制指标验证
[0108]
此处定义当k小于等于3时，认为直流电网的单极接地短路故障仅由近端换流站和次近端换流站决定。实际工程中，采用大地回线时，k约为1；采用金属回线时，k约等于3。因此，采用大地回线时单极接地故障电流主要由近端换流站和次近端换流站影响，而采用金属回线时单极接地故障电流由所有换流站影响。当系统增加特殊装置或改变参数使得k发生变化时，相应结论也即发生变化。
[0109]
实施例1分析结果如图11和12所示。从图11看出，大地回线故障电流主要由相邻和次相邻的换流站及其连接线决定。而且，增加了3个以上换流站的故障电流基本相同。在图12示了带金属返回的直流电网中的故障电流。在图12添加的换流站越多，实现的故障电流就越大，这表明所有换流站都影响故障电流。仿真结果与分析结果吻合较好。
[0110]
实施例2中，直流电压用于评估换流站的放电水平，其中较大的直流电压表示较低的放电水平，对应于对故障电流的微弱贡献。图13和14分别显示了具有接地回路和金属回路的五端直流电网中换流站的直流电压。
[0111]
从图13可以看出，在具有接地回路的直流电网中，相邻的换流站(换流站1和5)和次相邻的换流站(换流站2和4)对极地故障电流的贡献最大(95％以上)，而远距离换流站(换流站3)的贡献小于5％。对于基于金属回流的直流电网，从图14中可以看出，所有换流站的直流电压都降低到一个较大的现存。也就是说，所有相邻的、次相邻的和远处的换流站都以近似平均的水平对极地故障电流做出贡献。仿真结果验证了前面基于指标k的讨论结果。