适用于风储联合调频系统的功率优化分配控制方法及系统

1.本发明属于电气工程领域，更具体地，涉及一种适用于风储联合调频系统的功率优化分配控制方法及系统。


背景技术：

2.随着风电机组等新能源的大量接入电网，由于其发电设备不具备响应系统频率变化的惯量和一次调频能力，会影响系统的频率稳定性，单独依靠传统机组进行一次调频因调频容量有限难以满足调频需求。为了保证系统的频率稳定性，现有大多数风电机组已具备一定的调频能力。
3.除了风电场直接参与电网调频外，储能技术的快速发展也为调频提供了新的解决办法。储能系统响应速度快，能够快速控制双向功率，并且跟踪功率能力强，可以满足多种场景下的调频需求。为了有效改善电网的经济效益和调频性能，大部分现有风电机组和储能装置相结合共同参与系统的一次调频。
4.但是由于储能成本较高，进行风储联合调频时还需要考虑到风储调频的经济成本问题。因此，如何在满足一次调频要求的同时，兼顾风储联合调频成本最小已成为目前的关键问题。


技术实现要素：

5.针对现有技术的以上缺陷或改进需求，本发明提供了适用于风储联合调频系统的功率优化分配控制方法及系统，其目的在于在满足一次调频需求的同时，合理分配风储的输出功率，使调频成本最小化，由此提高风储联合参与调频的经济性。
6.为实现上述目的，按照本发明的一个方面，提供了一种适用于风储联合调频系统的功率优化分配控制方法，其包括：
7.采样k时刻风储联合调频系统的运行参数；
8.根据所述运行参数，在风储联合调频系统状态方程的基础上，建立优化模型，所述优化模型包括控制变量、目标函数和约束条件，其中，所述目标函数为预测时域n
p
内的单位时间调频成本函数，所述控制变量包括k时刻风机桨距角变化量的参考值δβ
ref
(k)和k时刻储能功率变化量的参考值δp
ref
(k)，所述约束条件包括满足调频需求的一次调频功率平衡条件约束p(k+i|k)＝δp
g
(k+i|k)+δp
wind
(k+i|k)+δp
bess
(k+i|k)，其中，p(k+i|k)为当前采样时刻k对k+i时刻系统一次调频功率需求的预测值，δp
g
(k+i|k)为当前采样时刻k对k+i时刻传统机组功率的预测值，δp
wind
(k+i|k)为当前采样时刻k对k+i时刻风电机组功率的预测值，δp
bess
(k+i|k)为当前采样时刻k对k+i时刻储能功率的预测值；i＝1,2,
···
,n
p
；
9.以所述目标函数的值取最小得到所述控制变量；
10.以所述控制变量中的k时刻风机桨距角变化量的参考值δβ
ref
(k)和k时刻储能功率变化量的参考值δp
ref
(k)再次作用于风储联合系统，对风储系统下一时刻的状态进行优化，即更新k+1时刻的系统状态。
11.优选地，所述目标函数为：其中，c为预测时域内风储联合调频系统的单位时间调频成本，c
wind
(k+i|k)为当前采样时刻k对k+i时刻风电机组调频成本的预测值，c
bess
(k+i|k)为当前采样时刻k对k+i时刻储能调频成本的预测值，n
p
为模型预测控制的预测时域。
12.优选地，所述约束条件还包括：
13.储能装置功率变化量约束：
‑
p
b
≤δp
ref
(k+i|k)≤p
b
，其中，δp
ref
(k+i|k)为当前采样时刻k对k+i时刻δp
ref
的预测值，p
b
为储能的额定功率；
14.风机桨距角变化量约束：δβ
ref
(k+i|k)≥
‑
(β0‑
β
min
)，δβ
ref
(k+i|k)≤(β
max
‑
β0)，其中，δβ
ref
(k+i|k)为当前采样时刻k对k+i时刻δβ
ref
的预测值，β
min
为桨距角的最小值，β
max
为桨距角的最大值，β0为初始桨距角。
15.储能荷电状态约束：s
min
≤s(k+i|k)≤s
max
，其中，s(k+i|k)为当前采样时刻k对k+i时刻荷电状态的预测值，s
min
为荷电状态的最小值，s
max
为荷电状态的最大值。
16.优选地，所述一次调频功率平衡条件约束还包括：
17.计算当前采样时刻k对k+i时刻系统一次调频功率需求的预测值p(k+i|k)，p(k+i|k)＝k
·
δf(k+i|k)，其中，p
load
(k+i|k)是以当前采样时刻k为基础的k+i时刻p
load
的绝对值，δf
ref
(k+i|k)为当前采样时刻k对k+i时刻根据系统一次调频达到要求的稳态频率偏差的设定值，δf(k+i|k)为当前采样时刻k对k+i时刻系统频率偏差δf的实时预测值。
18.优选地，所述成本函数其中，c
wind
(k+i|k)为当前采样时刻k对k+i时刻风电机组调频成本的预测值，c
bess
(k+i|k)为当前采样时刻k对k+i时刻储能调频成本的预测值，n
p
为模型预测控制的预测时域，
19.所述当前采样时刻k对k+i时刻风电机组调频成本的预测值c
wind
(k+i|k)＝a1·
δp
wind
(k+i|k)2，α1为风电机组功率偏移的成本系数，δp
wind
(k+i|k)为当前采样时刻k对k+i时刻风电机组功率的预测值；
20.所述当前采样时刻k对k+i时刻储能调频成本的预测值c
bess
(k+i|k)＝a2·
δp
bess
(k+i|k)2+a3·
(s(k+i|k)
‑
s
ref
(k+i|k))2，α2为储能功率偏移的成本系数，α3为储能荷电状态偏移的成本系数，δp
bess
(k+i|k)为当前采样时刻k对k+i时刻储能输出功率的预测值，s(k+i|k)为当前采样时刻k对k+i时刻储能荷电状态的预测值，s
ref
(k+i|k)为当前采样时刻k对k+i时刻储能荷电状态参考值的设定值。
21.按照本发明的另一方面，提供了适用于风储联合调频系统的功率优化分配控制系统，包括：计算机可读存储介质和处理器；
22.所述计算机可读存储介质用于存储可执行指令；
23.所述处理器用于读取所述计算机可读存储介质中存储的可执行指令，执行本发明第一方面所述的适用于风储联合调频系统的功率优化分配控制方法。
24.通过本发明所构思的以上技术方案，与现有技术相比，能够取得以下有益效果：
25.1、本发明提供的适用于风储联合调频系统的功率优化分配控制方法及系统在调频效果方面，采用以一次调频功率平衡条件为约束的技术手段，不仅使调频偏差稳定在要求范围以内，而且加快了调频的速度。
26.2、本发明提供的适用于风储联合调频系统的功率优化分配控制方法及系统采用以目标函数最小的技术手段，使调频过程中风机和储能的功率进一步得到优化分配，从而使风储联合系统的调频成本最小，满足了经济性。
附图说明
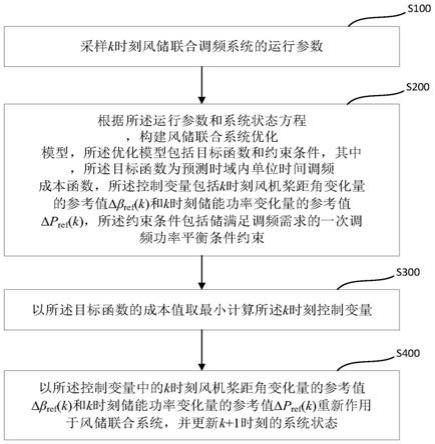
27.图1为本发明实施例提供的一种适用于风储联合调频系统的功率优化分配控制方法的流程框图；
28.图2为交流负荷变化情况；
29.图3为采用本发明实施例提供的适用于风储联合调频系统的功率优化分配控制方法的电网频率变化曲线；
30.图4(a)为传统机组的输出功率变化曲线；
31.图4(b)为风储系统的输出功率变化曲线；
32.图5(a)为风电机组的输出功率变化曲线；
33.图5(b)为储能装置的输出功率变化曲线；
34.图6为储能的荷电状态变化曲线。
具体实施方式
35.为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间不构成冲突就可以相互组合。
36.如图1所示为本技术实施例中的适用于风储联合调频系统的功率优化分配控制方法的流程图，该方法包括：
37.步骤s100：采样k时刻风储联合调频系统的运行参数。
38.具体地，运行参数包括k时刻调速器位置增量p
v
(k)，k时刻再热器输出功率增量p
m
(k)，k时刻传统机组输出功率变化量δp
g
(k)，k时刻储能输出功率变化量δp
bess
(k)，k时刻风机桨距角变化量δβ(k)，k时刻风机输出功率变化量δp
wind
(k)，k时刻储能荷电状态s(k)，k时刻系统输出频率变化量δf(k)，k时刻交流母线上负荷变化量p
load
(k)。
39.步骤s200：根据所述运行参数和系统状态方程，构建风储联合系统优化模型，所述优化模型包括控制变量、目标函数和约束条件，其中，所述目标函数为预测时域内单位时间调频成本函数，所述控制变量包括k时刻风机桨距角变化量的参考值δβ
ref
(k)和k时刻储能功率变化量的参考值δp
ref
(k)，所述约束条件包括储满足调频需求的一次调频功率平衡条件约束。
40.具体地，目标函数为基于k时刻控制变量的成本函数，控制变量包括：在每次采样时刻k，风机桨距角变化量的参考值δβ
ref
(k)，储能功率变化量的参考值δp
ref
(k)。
41.目标函数为预测时域内风储联合系统的单位时间调频成本c，主要包括两部分：当
前采样时刻k对k+i时刻风电机组调频成本的预测值c
wind
(k+i|k)和当前采样时刻k对k+i时刻储能调频成本的预测值c
bess
(k+i|k)：
[0042][0043]
在本实施例中，当前采样时刻k对k+i时刻风电机组调频成本的预测值c
wind
(k+i|k)主要包括风电机组功率偏移成本。其函数关系如下所示：
[0044]
c
wind
(k+i|k)＝a1·
δp
wind
(k+i|k)2[0045]
式中：α1为风电机组功率偏移的成本系数，δp
wind
(k+i|k)为当前采样时刻k对k+i时刻风电机组功率的预测值。
[0046]
当前采样时刻k对k+i时刻储能调频成本的预测值c
bess
(k+i|k)主要包括储能功率偏移成本和荷电状态偏移成本。其函数关系如下所示：
[0047]
c
bess
(k+i|k)＝a2·
δp
bess
(k+i|k)2+a3·
(s(k+i|k)
‑
s
ref
(k+i|k))2[0048]
式中：α2为储能功率偏移的成本系数，α3为储能荷电状态偏移的成本系数，δp
bess
(k+i|k)为当前采样时刻k对k+i时刻储能输出功率的预测值，s(k+i|k)为当前采样时刻k对k+i时刻储能荷电状态的预测值，s
ref
(k+i|k)为当前采样时刻k对k+i时刻储能荷电状态参考值的设定值。
[0049]
按照一般标准，一次调频的稳态频差绝对值不应超过0.2hz，若系统只依靠火电机组一次调频，其在满足频率偏差要求的基础上，稳态时系统能达到的最大出力为δp
g.max
，即：
[0050]
δp
g.max
＝(
‑
1/r
‑
d)
·
δf
ref
(δf
ref
＝
±
0.2hz)
[0051]
其中，r为火电机组一次调频的调差系数，d为负荷调节系数。
[0052]
当|p
load
(k+i|k)|＜|δp
g.max
|时，仅需依靠火电机组一次调频即可达到调频要求，不需要风储出力，其中p
load
(k+i|k)是以当前采样时刻k为基础的k+i时刻p
load
的绝对值。
[0053]
当|p
load
(k+i|k)|＞|δp
g.max
|时，此时需要风储联合系统适当输出来改善调频性能，使系统达到调频要求，同时为了尽量降低风储出力成本，设置一次调频达到要求的最终频率稳定值为
±
0.2hz，当p
load
>0时，δf
ref
＝
‑
0.2hz；当p
load
<0时，δf
ref
＝0.2hz。
[0054]
将风储和电网看作一个整体，当需要风储系统出力时，在此设计整个系统的一次调频等效下垂系数k：
[0055][0056]
式中，p
load
(k+i|k)是以当前采样时刻k为基础的k+i时刻p
load
的绝对值，δf
ref
(k+i|k)为当前采样时刻k对k+i时刻根据系统一次调频达到要求的稳态频率偏差的设定值。
[0057]
则系统一次调频功率需求的实时预测值为：
[0058]
p(k+i|k)＝k
·
δf(k+i|k)
[0059]
式中，δf(k+i|k)为当前采样时刻k对k+i时刻系统频率偏差δf的实时预测值。
[0060]
在本实施例中，约束条件包括满足一次调频需求的功率平衡条件约束p(k+i|k)＝δp
g
(k+i|k)+δp
wind
(k+i|k)+δp
bess
(k+i|k)，其中，p(k+i|k)为当前采样时刻k对k+i时刻系统一次调频功率需求的预测值，δp
g
(k+i|k)为当前采样时刻k对k+i时刻传统机组功率的预测值，δp
wind
(k+i|k)为当前采样时刻k对k+i时刻风电机组功率的预测值，δp
bess
(k+i|
k)为当前采样时刻k对k+i时刻储能功率的预测值。
[0061]
在本实施例中，约束条件还包括储能装置功率变化量约束、风机桨距角变化量约束、储能荷电状态约束。
[0062]
具体地，储能功率变化量约束如下，其表示储能用于调频的功率不超过其额定功率：
[0063]
‑
p
b
≤δp
ref
(k+i|k)≤p
b
[0064]
其中，δp
ref
(k+i|k)为当前采样时刻k对k+i时刻δp
ref
的预测值，p
b
为储能的额定功率。
[0065]
风机桨距角变化量约束如下，其表示风机用于调频的桨距角不能超过液压伺服系统的控制范围：
[0066]
δβ
ref
(k+i|k)≥
‑
(β0‑
β
min
)，δβ
ref
(k+i|k)≤(β
max
‑
β0)
[0067]
其中，δβ
ref
(k+i|k)为当前采样时刻k对k+i时刻δβ
ref
的预测值，β
min
为桨距角的最小值，β
max
为桨距角的最大值，β0为初始桨距角。
[0068]
储能荷电状态约束如下，其表示储能的荷电状态不能超过上下限值：
[0069]
s
min
≤s(k+i|k)≤s
max
[0070]
其中，s(k+i|k)为当前采样时刻k对k+i时刻荷电状态的预测值，s
min
为荷电状态的最小值，s
max
为荷电状态的最大值。
[0071]
通过以上公式构建出风储联合系统的优化模型后，需要对该模型进行求解，因此，该方法还包括：
[0072]
步骤s300：以所述目标函数的成本值取最小计算所述k时刻控制变量。
[0073]
在步骤s200所述的目标函数和约束条件下，利用线性优化求解器对优化模型求解，所得结果中的控制变量包含了一段时间的控制变量序列[δβ
ref
(k)，δp
ref
(k)，δβ
ref
(k+1)，δp
ref
(k+1)，
……
，δβ
ref
(k+n
c
)，δp
ref
(k+n
c
)]，其中，n
c
为控制时域。
[0074]
计算出最优控制变量序列[δβ
ref
(k)，δp
ref
(k)，δβ
ref
(k+1)，δp
ref
(k+1)，
……
，δβ
ref
(k+n
c
)，δp
ref
(k+n
c
)]后，该方法还包括：
[0075]
步骤s400：以所述控制变量中的k时刻风机桨距角变化量的参考值δβ
ref
(k)和k时刻储能功率变化量的参考值δp
ref
(k)重新作用于风储联合系统，并更新k+1时刻的系统状态，直至结束。
[0076]
以下以一具体的实施例验证本技术的适用于风储联合调频系统的功率优化分配控制方法的调频效果和经济性，随机产生如图2所示的变化负荷，并且设置每40s变化一次，用于尽可能模拟实际情况的干扰信号。
[0077]
系统的频率偏差变化曲线为图3，由图3可以发现，本技术的适用于风储联合调频系统的功率优化分配控制方法使系统的频率偏差在一定程度上减小了，并且始终能够保持稳态频差绝对值不超过0.2hz，改善了系统的调频效果。
[0078]
另外，传统机组和风储系统的输出功率变化曲线分别为图4(a)和图4(b)，风电机组和储能装置的输出功率变化曲线分别为图5(a)和图5(b)，储能的荷电状态变化曲线为图6。
[0079]
由图4(a)和图4(b)可知当负荷变化较大时，仅靠火电机组不能满足稳态频差要求，此时风储会适当快速出力；当负荷变化较小时，可仅靠火电机组调频，此时风储整体上
不出力，具体情况如图4(b)中的120s～160s，280s～320s和400s～440s时间段所示，但是由图5(a)，图5(b)和图6可知，由于储能的soc偏移成本影响，这几个时间段内的储能仍会适当出力使soc尽量接近基准值0.5，而这部分出力会由风机来补充。
[0080]
另外，由图4(a)和图4(b)可知在每次较大负荷突变开始的一段时间，由于传统机组响应时间较慢，风储系统的有功会在短时间内增大以满足调频功率需求，之后随着传统机组出力的慢慢增大并趋于稳定，风储总出力会逐渐减小并趋于稳定。并且由图5(a)和图5(b)可知，由于储能变流器响应时间常数比风机桨距角控制响应时间常数更小，所以储能的响应速度比风机更快；另外，在调频过程中为了使调频成本最小，在风储总出力逐渐趋于稳定阶段，风机和储能的功率仍会随着时间的变化而改变。具体来说，由图5(a)和图5(b)可知，由于风储功率偏移成本系数的不同以及储能soc偏移成本的影响，在调频过程中储能调频成本较高，风机调频成本较低，故为了使调频过程中风储的调频总成本最低，风储总出力稳定后在风储内部中储能的功率会慢慢减小，风机的功率会慢慢增大，验证了本技术的适用于风储联合调频系统的功率优化分配控制方法的经济性。
[0081]
本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。