一种风电场一次调频控制系统的制作方法

1.本发明涉及新能源领域中风力发电的调频控制领域，具体而言，涉及一种风电场一次调频控制系统。


背景技术：

2.风力发电作为最突出的可再生资源之一，近年来得到了迅速的发展。随着风力发电在电力系统中的占比份额提高，风电场替代传统电厂的增多，由于风电机组具有弱支撑性和低抗扰性的缺点，必然会降低系统惯性，恶化电力系统的频率响应。由于风力涡轮机通过功率转换器与电网相连，其转子转速与系统频率解耦。此外，它通常工作在最大功率点跟踪模式下，没有频率支持能力。并且风力发电机组的有功调节能力不足，会导致风力发电接入电力系统的频率控制能力不断下降，影响到电网运行的稳定性。在这种情况下，改进风电场的频率支持能力已经成为许多国家的需求。
3.现阶段对风电场实际运行进行减载以预留出一定的调频容量,从而在发生频率事件时提供功率支撑，但是长期减载运行会显著影响风电场的运行经济性。
4.目前市场上已经投入使用的非线性模型预测控制能够对于风电场频率进行调节，但是，这种预测控制方法要集中解决包括大量输入变量的参数优化问题，涉及到很大的计算量。因此需要针对于这种大计算运算控制系统进行设计一种改进的方法。


技术实现要素：

5.针对上述不足，本发明进一步完善了非线性模型预测控制控制技术，在集中式非线性模型预测控制的基础上提出了基于分层控制的分层式非线性模型预测控制风电场一次调频控制系统。
6.一种具有层次结构的风电场一次调频控制系统，其特征在于，包括：
7.一个频率支持控制器、一个中央控制器和若干个风力涡轮机控制器；频率支持控制器输出信号给中央控制器，中央控制器与若干个风力涡轮机控制器通信连接；
8.频率支持控制器为整个风电场提供功率基准将风电场的功率基准发送到中央控制器。中央控制器与若干个风力涡轮机控制器之间进行信息传递；
9.通过一个分层式非线性模型预测控制分配到每一个风力涡轮机；
10.利用分层式非线性模型求解耦合子问题和解耦子问题；中央控制器解决耦合子问题，而每一个风力涡轮机上的单个控制器解决解耦子问题。
11.本发明的技术方案的优点：
12.(1)现代风力发电领域对于电网调频技术还不够完善，在一次调频技术方面还有待提高。
13.(2)大型风场运行时进行并网的频率调整技术需要进一步优化设计，目前所使用的一些控制方案在面对大型风场的庞大数据量时会影响到控制系统的响应快速性进而影
响到电网的稳定性。
14.(3)目前风电场一般采用最大功率跟踪控制的方式运行，即“来多少风，发多少电”，这就加剧了电网有功功率不平衡的风险，势必引起频率波动变大。需要设计一款调频控制系统将随机的风力发电网络进行预测控制，使得电网稳定性大大提高。
15.(4)利用分层求解的方法将控制系统分为若干个模块，对于每个扩展模块进行任务划分，使得中央处理器的技术负担大大减轻。
16.通过本发明所提出的控制技术，实现了非线性模型预测控制风电场一次调频技术的优化控制，使得系统响应和快速性得到进一步提升，大大提高了风电场运行稳定性。
17.通过分层求解非线性模型预测控制优化问题，可以显著减轻中央控制器的计算负担。与集中式非线性模型预测控制相比，可减少多达50％的计算时间。这避免了对高性能计算设备的要求，使分层式非线性模型预测控制在大型风电场的实施中具有优势。并且，分层式非线性模型预测控制的通信拓扑结构与传统的集中控制相同。这避免了对通信网络的修改，并使分层式非线性模型预测控制易于在现有风力发电场实施。
附图说明
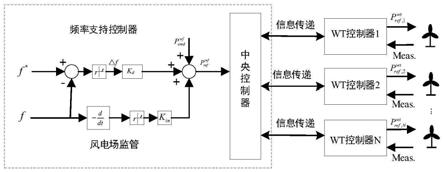
18.图1风力发电场的分级控制框架；
19.图2h-nmpc流程图。
具体实施方式
20.下面结合附图对本发明作进一步描述，应当理解，此处所描述的内容仅用于说明和解释本发明，并不用于限定本发明。
21.缩略语、英文和关键术语定义列表
22.1、wt:风力涡轮机(wind turbine)
23.2、mppt：最大功率点跟踪(maximum power point tracking)
24.3、nmpc：非线性模型预测控制(nonlinear model predictive control)
25.4、c-nmpc：集中式nmpc
26.5、h-nmpc：分层式nmpc
27.6、qp：二次规划(quadratic programming)
28.7、sqp：序列二次规划(sequential quadratic programming)
29.8、admm：交替方向乘子法(alternating direction method of multipliers)
30.9、nlp：非线性规划(nonlinear programming)
31.非线性模型预测控制能够处理风力机的非线性动态约束，已被应用于风电场的频率支持。风电场的风电机组单元数量多、协调控制与稳定运行困难，需从场站级提出解决方案。然而，集中式非线性模型预测控制由于要解决包含大量变量的嵌入式优化问题，计算量大，需要高性能的计算设施。
32.为了解决这一问题，对集中式非线性模型预测控制进行了改进，构造一种新的具有层次结构的风力发电频率支持系统。利用其部分可分离的结构，将非线性模型预测控制优化问题分解为一个耦合子问题和几个解耦子问题。小波变换控制器以并行的方式局部解决解耦子问题，然后将灵敏度和活动集信息发送给中心控制器。然后，位于风电场的中央控
制器立即求解耦合子问题，并计算牛顿方向进行下一次迭代。与集中式非线性模型预测控制的集中计算相比，分层式非线性模型预测控制大大减少了中央控制器的计算负担，在不损失最优性的前提下提高了非线性模型预测控制的效率。数值模拟结果进一步验证了分层式非线性模型预测控制的有效性和效率。
33.如图1所示，构造风电场一次调频控制系统的分层控制框架。
34.风电场调节层包括一个频率支持控制器、一个中央控制器和若干个风力涡轮机控制器。频率支持控制器为整个风电场提供功率基准频率支持控制器包括惯性仿真回路和下垂控制回路，具体来说，等于来自电力系统合作者的功率调度命令加上惯性仿真和下垂控制回路的输出。f是在公共耦合点的频率，f
*
是标称频率。δf＝f
*-f为频率偏差。惯性仿真回路和下垂控制回路分别给出了惯性系数和下垂系数。可以对惯性系数和下垂系数进行优化，以保证频率支持性能。在输出为δf
±
0.02hz处设置死区，防止风电场输出功率波动。
35.下一步，将风电场的功率基准发送到中央控制器。中央控制器与若干个风力涡轮机控制器之间进行信息传递。
36.通过构造一个分层式非线性模型预测控制分配到每一个风力涡轮机并保证其稳定性。为了减少中央控制器的计算量，将非线性模型预测控制优化问题分解为若干子问题，并采用分层的方式进行求解。
37.具体来说，中央控制器解决耦合子问题，而每一个风力涡轮机上的单个控制器解决解耦子问题。其基本控制原理，利用非线性模型预测控制优化问题的部分可分离结构，将问题分解为一个耦合子问题和几个解耦子问题。解耦子问题是一种只与单个风力涡轮机的动力学有关的小规模优化问题。因此，风力涡轮机控制器采用小波变换控制器就可以有效地并行求解。其次，通过分层求解非线性模型预测控制优化问题，大大减轻了中央控制器的计算负担，降低了设备的性能要求。
38.大多数计算昂贵的数值运算，如非凸极小化和导数计算，都分配给小波控制器。中央控制器只解决具有等式约束的二次规划子问题，是一种计算成本低廉的数值运算。
39.小波控制器的解耦子问题
40.每个小波可以变换为一个解耦优化问题，通过应用对偶分解和增广拉格朗日式，解耦优化问题可被表示为：
[0041][0042]
s.t.gi(zi)≤0|ki,i＝1,2,...,n
ꢀꢀꢀ
(8)
[0043]
其中为局部优化变量；z
u,i
∈rh和z
x,i
分别是与控制输入轨迹相关的变量和第i个风力涡轮机的状态变量轨迹；γ∈r
+
为惩罚参数；ki∈r
3h
是约束的对偶变量。
[0044]
进一步可以建立一个无约束二次规划子问题：
[0045][0046]zn+1
为与s相关的局部优化变量。
[0047]
中央控制器的耦合子问题
[0048]
对于中央控制器，构造一个耦合的二次规划子问题，得到原始变量zi的牛顿迭代δzi和下一个迭代的对偶变量y。
[0049]
建立耦合子问题，即牛顿迭代，hessian矩阵hi，梯度gi和雅可比矩阵ci的元素c
i，j
，计算基于解耦子问题(1)-(3)的解。
[0050][0051]
其中，gi∈r
2h+1
；hi∈r
(2h+1)*(2h+1)
(i＝1,
…
,n)；g
n+1
∈rh；h
n+1
∈r
h*h
。ci＝[c
i，1
，c
i，2
，
…
，c
i，2h
]
t
∈r
2h*(2h+1)
。
[0052]
根据式(4)，耦合的二次规划子问题可以表示为:
[0053][0054]
其中y
qp
∈rh是耦合约束的对偶变量。μ∈r
+
是惩罚参数。引入松弛变量δ∈rh以保证问题的可解性。
[0055]
可以看出，本方法求解的二次规划子问题(5)与增广拉格朗日序列二次规划方法求解的二次规划问题相似。唯一的区别是耦合二次规划子问题的活动集(即满足不等式约束的指标为等式)是通过解耦子问题推测出来的，并由ci的非零行表示。利用活动集的推测，将耦合二次规划子问题(5)中的为活动不等式约束强制为等式约束。因此，解决这个问题相当于解决一个线性方程组，这可替换廉价的计算数值运算。
[0056]
非线性模型预测控制优化问题首先被分解为耦合的二次规划子问题、非耦合的非线性规划子问题和非耦合的二次规划子问题。然后用阿拉丁法求解。与交替方向乘子法相似，求解过程包括两个阶段：并行阶段和一致性阶段。
[0057]
在并行阶段阶段，(ζi,y)y∈rh与通过求解基于当前原始迭代和对偶迭代的解耦子问题得到牛顿迭代泰勒级数逼近的线性化点zi同为对偶变量。基于耦合子问题的解，更新下一次迭代的原始迭代和对偶迭代(ζi,y)，通过迭代执行这两个阶段，直到满足停止准则，得到原优化问题的解。
[0058]
具体解算方法如下：
[0059]
步骤一：初始化
[0060]
迭代数r设为0，对于解耦子问题，每个小波变换控制器根据其状态初始化原始变
量拉格朗日乘数y0和惩罚参数γ。对于耦合子问题，中央控制器初始化惩罚参数μ和终止容限ε。
[0061]
步骤二：并行求解解耦子问题
[0062]
在每个小波变换控制器上并行求解解耦的非线性规划子问题(1)-(2)。这是与小波变换动力学相关的小规模优化问题，可以用原始内点算法有效地解决。与松弛变量相关的解耦二次规划子问题(3)可以由任意一个小波变换控制器使用参数活动集方法求解。
[0063]
步骤三：的计算
[0064]
基于解耦子问题的解，每个小波变换控制器通过式(4)计算梯度hessian矩阵和雅可比逼近并将它们发送给中心控制器，而且计算也是并行进行的。
[0065]
步骤四：求解耦合子问题的解
[0066]
从风力涡轮机控制器接收和中央控制器求解耦合的二次规划子问题(5)，得到δzi和y
qp
。
[0067]
步骤五：和y
[r+1]
数值的更新
[0068]
中央控制器更新原始变量和对偶变量y
[r+1]
作为下一个迭代步骤，然后将它们发送给小波控制器。
[0069][0070]
步骤六：迭代求解停止
[0071]
通过对解耦子问题(1)、(3)和耦合子问题(5)进行迭代求解，得到nmpc优化问题的解。迭代将停止，直到满足以下停止标准。
[0072][0073]
最后应说明的是：以上所述仅为本发明的解释，并不用于限制本发明，尽管对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。