一种表贴式永磁同步电机参数辨识方法

1.本发明属于永磁同步电机驱动控制应用领域，尤其是涉及一种表贴式永磁同步电机参数辨识方法。


背景技术：

2.永磁同步电机是同步电机的一种，由多极化永磁转子和带有绕组的定子这两个关键部件组成。因其效率高、转矩大、体积小等优点，在工业自动化领域的运行控制中都扮演了重要的角色。永磁同步电机又分为表贴式永磁同步电机和内置式永磁同步电机两种，对于表贴式永磁同步电机而言，在结构上，其交直轴磁阻的差异很小，相应的交直轴电感的差异也很小，所以表贴式永磁同步电机永磁体的用量较小，更容易产生正弦波磁动势。在实际应用中，由于永磁同步电机的非线性和强耦合性，电机的参数也将随着运行过程发生变化。在参数辨识领域，主要辨识方法分为在线参数辨识和离线参数辨识。常见的参数识别方法有递推最小二乘法、神经网络算法和kalman滤波算法等。递推最小二乘法算法结构简单，易于实现，但该算法比较适用于定常未知参数系统。


技术实现要素：

3.发明目的：为了解决表贴式永磁同步电机参数辨识的可观性问题，提出了一种基于位置角信号注入的方法。与传统的向d轴注入负电流相比，不会影响电机的转速性能，此外由于电感参数与电流有关，所以新的方法也保障了辨识的真实性。因此，提出一种表贴式永磁同步电机参数辨识方法，保证表贴式永磁同步电机参数辨识的精度。
4.技术方案：为实现上述发明目的，本发明所采用的技术方案如下：
5.本发明提供一种表贴式永磁同步电机参数辨识方法，实施步骤包括：
6.步骤1，位置角信号的注入：通过对位置信号注入一个周期性的方波，形成两种d-q轴电压状态；
7.步骤2，验证可观性：联立所形成两种d-q轴电压状态方程，根据非线性系统的可观性原理，利用李导数，证明出系统是可观的；
8.步骤3，参数的解耦：对各种不同的电压状态方程进行处理，实现对各个参数解耦；
9.步骤4，递归最小二乘法的参数辨识：利用递归的最小二乘法观测器，根据解耦出来的方程，实现对各个参数的在线辨识。
10.进一步，所述步骤1的具体过程为：
11.表贴式永磁电机在两相旋转坐标系的电压方程可表示为
[0012][0013]
其中，ud和uq为d-q轴的电压，id和iq为d-q轴的电流，ωe是电角速度，ψf为电机转子磁链，rs为电机的定子电阻，ls为电机定子电感。
[0014]
通过向位置角信号注入一个幅值为δθ，占空比为50％的周期性方波，根据坐标变
换，新的d-q轴的电压和电流可表示为
[0015][0016][0017]
根据i
d’＝0的控制方式，实际的d-q轴电流为
[0018][0019][0020]
此时id和iq为注入位置角信号后的d-q轴电流，id‘
和iq‘
为注入位置角信号前的d-q轴电流，i
q*
为参考的q轴电流，δθ为注入的位置角信号。
[0021]
因此，注入后的d-q轴电压方程为
[0022][0023]
进一步，步骤2所述的具体过程为：
[0024]
根据非线性系统的一般表达式，具体为
[0025][0026]
y＝h(x)
[0027]
其中，x是状态向量，是状态向量的导数，f、h分别是对应的函数表达式，u是控制向量，y是输出向量。
[0028]
对于这样一个非线性系统，其中某一状态x0，定义一个o矩阵，表示为
[0029][0030]
n为状态向量x的维数，p为输出向量y的维数。
[0031]
其中l为可观性辨别矩阵，定义如下
[0032][0033][0034][0035]
其中ld与lq分别为为电机交直轴电感。
[0036]
根据非线性体统的一般表达式，由于内置式与表贴式的永磁同步电机可观性证明相同，考虑到普适性，根据内置式永磁同步电机d-q轴电压方程，可以将其改写如下
[0037][0038][0039][0040]
假定电阻、电感、磁链在短时间内不发生变化。根据非线性系统的定义，可以构造如下形式
[0041]
x＝[id,iq,rs,ld,lq,ψf]
τ
[0042]
y＝h(x)＝[id,iq]
τ
[0043]
u＝[ud,uq,ωe]
τ
[0044][0045]
其0到5阶李导数
[0046]
l
f0
h＝h＝[id,iq]
τ
[0047][0048][0049][0050][0051][0052]
为h对f的n阶李导数，代表梯度。
[0053]
其中，a为
[0054][0055]
根据可观性的原理，就要求o
12
×6满秩，利用0到5阶李导数，o
12
×6矩阵如下所示
[0056]
由于o
12
×6矩阵前两列已经满秩，所以只需要辨别o
12
×6矩阵的子矩阵o4×4’
，具体如下
[0057][0058]
在瞬时状态下，即时，矩阵o4×4’
满秩，此时系统可观。但在稳态情况时，即时，o4×4’
化简如下
[0059][0060]
此时o4×4’
秩为2。同理，对于表贴式永磁同步电机而言，其中的o3×3’
秩也为2，它们都是不可观的。
[0061]
进一步，所述步骤3的具体过程为：
[0062]
注入位置角信号后的表贴式永磁同步电机d-q轴电压方程状态为
[0063][0064]
ud‘
和uq‘
为注入位置角信号后的d-q轴电压。
[0065]
未注入位置角信号后的表贴式永磁同步电机d-q轴电压方程状态为
[0066][0067]
通过相关运算得到各个参数的计算方法，实现各个参数之间的解耦运算，具体如下
[0068][0069]
[0070][0071]
为辨识的定子电感，为辨识的转子磁链，为辨识的定子电阻。
[0072]
由于注入位置角信号取一个非常小的值，那么sinδθ≈δθ，cosδθ≈1，所以
[0073]
进一步，所述步骤4的具体过程为：
[0074]
对于一组数据{yi∈r,xi∈rn,i＝1,
…
,n}，满足
[0075][0076]
辨识n
×
1维参数向量θ＝[θ1,
…
,θn]
[0077]
形式改写为
[0078]yn
＝xnθ
[0079]
目标是最小化估计误差，表示为
[0080][0081]
对求导
[0082][0083][0084][0085]
其中，yn∈rn，xn是个n
×
n的矩阵，每一行对应一个为估计的参数。
[0086]
定义一个修正量m，进行递推运算，更新模型的参数，具体如下
[0087][0088]
下标t与t-1分别代表t时刻与t-1时刻。
[0089]
定义一个变量p
n-1
＝(x
nt
xn)，那么
[0090][0091]
同理就有如下表达式
[0092][0093][0094]
pn＝(p
n-1-1
+xnx
nt
)-1
[0095]
根据矩阵逆引理，对递推最小二乘法求解
[0096]
pn＝p
n-1-p
n-1
xn[i+x
nt
p
n-1
xn]-1
x
nt
p
n-1
[0097][0098]
本发明的有益效果：
[0099]
1)本发明提出的基于位置角信号注入的方法，能够有效的解决参数辨识的可观性问题，同时不影响转速性能，保证了辨识的准确性；
[0100]
2)本发明采用多种状态之间简单运算的方法，实现简单，还起到了参数之间解耦的作用；
[0101]
3)本发明利用递归的最小二乘法观测器，实现了在线的参数辨识，具有收敛速度快、占用内存少、精度较高等优点。
附图说明
[0102]
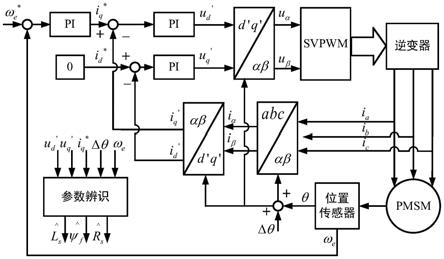
图1为表贴式永磁同步电机参数辨识原理图
[0103]
图2为参数辨识的递归最小二乘法原理图
[0104]
图3为位置信号注入时序图
[0105]
图4为电感真实值与辨识仿真结果对比图
[0106]
图5为磁链真实值与辨识仿真结果对比图
[0107]
图6为电阻真实值与辨识仿真结果对比图
具体实施方式
[0108]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用于解释本发明，并不用于限定本发明。
[0109]
如图1所示，本发明提出一种表贴式永磁同步电机参数辨识方法。
[0110]
所提出的一种表贴式永磁同步电机参数辨识方法的具体实施步骤包括：
[0111]
步骤1：位置角信号的注入
[0112]
表贴式永磁电机在两相旋转坐标系的电压方程可表示为
[0113][0114]
其中，ud和uq为d-q轴的电压，id和iq为d-q轴的电流，ωe是电角速度，ψf为电机转子磁链，rs为电机的定子电阻，ls为电机定子电感。
[0115]
通过向位置角信号注入一个幅值为δθ，占空比为50％的周期性方波，根据坐标变换，新的d-q轴的电压和电流可表示为
[0116][0117]
[0118]
根据i
d’＝0的控制方式，实际的d-q轴电流为
[0119][0120][0121]
此时id和iq为注入位置角信号后的d-q轴电流，id‘
和iq‘
为注入位置角信号前的d-q轴电流，i
q*
为参考的q轴电流，δθ为注入的位置角信号。
[0122]
因此，注入后的d-q轴电压方程为
[0123][0124]
步骤2，验证可观性
[0125]
根据非线性系统的一般表达式，具体为
[0126][0127]
y＝h(x)
[0128]
其中，x是状态向量，是状态向量的导数，f、h分别是对应的函数表达式，u是控制向量，y是输出向量。
[0129]
对于这样一个非线行系统，其中某一状态x0，定义一个o矩阵，表示为
[0130][0131]
n为状态向量x的维数，p为输出向量y的维数。
[0132]
其中l为可观性辨别矩阵，定义如下
[0133][0134][0135][0136]
其中ld与lq分别为为电机交直轴电感。
[0137]
根据非线性体统的一般表达式，由于内置式与表贴式的永磁同步电机可观性证明相同，考虑到普适性，根据内置式永磁同步电机d-q轴电压方程，可以将其改写如下
[0138][0139][0140][0141]
假定电阻、电感、磁链在短时间内不发生变化。根据非线性系统的定义，可以构造
如下形式
[0142]
x＝[id,iq,rs,ld,lq,ψf]
τ
[0143]
y＝h(x)＝[id,iq]
τ
[0144]
u＝[ud,uq,ωe]
τ
[0145][0146]
其0到5阶李导数
[0147]
l
f0
h＝h＝[id,iq]
τ
[0148][0149][0150][0151][0152][0153]
为h对f的n阶李导数，代表梯度。
[0154]
其中，a为
[0155][0156]
根据可观性的原理，就要求o
12
×6满秩，利用0到5阶李导数，o
12
×6矩阵如下所示
[0157]
由于o
12
×6矩阵前两列已经满秩，所以只需要辨别o
12
×6矩阵的子矩阵o4×4’
，具体如下
[0158][0159]
在瞬时状态下，即时，矩阵o4×4’
满秩，此时系统可观。但在稳态情况时，即时，o4×4’
化简如下
[0160][0161]
此时o4×4’
秩为2。同理，对于表贴式永磁同步电机而言，其中的o3×3’
秩也为2，它们都是不可观的。
[0162]
步骤3，参数的解耦
[0163]
注入位置角信号后的表贴式永磁同步电机d-q轴电压方程状态为
[0164][0165]
ud‘
和uq‘
为注入位置角信号后的d-q轴电压。
[0166]
未注入位置角信号后的表贴式永磁同步电机d-q轴电压方程状态为
[0167][0168]
通过相关运算得到各个参数的计算方法，实现各个参数之间的解耦运算，具体如下
[0169][0170][0171][0172]
为辨识的定子电感，为辨识的转子磁链，为辨识的定子电阻。
[0173]
由于注入位置角信号取一个非常小的值，那么sinδθ≈δθ，cosδθ≈1，所以
[0174]
步骤4，递归最小二乘法的参数辨识
[0175]
对于一组数据{yi∈r,xi∈rn,i＝1,
…
,n}，满足
[0176][0177]
辨识n
×
1维参数向量θ＝[θ1,
…
,θn]
[0178]
形式改写为
[0179]yn
＝xnθ
[0180]
目标是最小化估计误差，表示为
[0181][0182]
对求导
[0183][0184][0185][0186]
其中，yn∈rn，xn是个n
×
n的矩阵，每一行对应一个为估计的参数。
[0187]
定义一个修正量m，进行递推运算，更新模型的参数，具体如下
[0188][0189]
下标t与t-1分别代表t时刻与t-1时刻。
[0190]
定义一个变量p
n-1
＝(x
nt
xn)，那么
[0191][0192]
同理就有如下表达式
[0193][0194][0195]
pn＝(p
n-1-1
+xnx
nt
)-1
[0196]
根据矩阵逆引理，对递推最小二乘法求解
[0197]
pn＝p
n-1-p
n-1
xn[i+x
nt
p
n-1
xn]-1
x
nt
p
n-1
[0198][0199]
图4、图5和图6分别为电机实际电感与辨识电感、实际磁链与辨识磁链、实际电阻与辨识电阻的对比图。由图可知，它们的辨识估计值与实际值基本吻合。
[0200]
以上实施例仅用于说明本发明的设计思想和特点，其目的在于使本领域内的技术人员能够了解本发明的内容并据以实施。所以，凡依据本发明所揭示的原理、设计思路所作的等同变化或修饰，均在本发明的保护范围之内。