用于操作直线电动机的方法与流程

用于操作直线电动机的方法
1.本发明涉及一种用于操作直线电动机的方法，该直线电动机具有其上布置有多个驱动线圈的定子，并且具有其上布置有多个驱动磁体的沿该定子移动的传输单元，其中通过在该传输单元的驱动磁体的区域中向驱动线圈通电，产生与该传输单元的驱动磁体相互作用以移动该传输单元的电磁场。
2.在直线电动机中设有初级部件以及相对于该初级部件可移动地布置的次级部件(转子)。驱动线圈布置在初级部件上，并且驱动磁体布置在次级部件上，反之亦然。驱动磁体被实施为永磁体、电线圈或短路绕组。驱动线圈是为了产生电磁场而通电的电线圈。通过驱动磁体和驱动线圈的(电)磁场的相互作用，力作用于次级部件，其使该次级部件相对于初级部件移动。例如，直线电动机可被实施为同步机或异步机。直线电动机也可被实施为平面直线电动机(也称为平面电动机)。直线电动机的驱动线圈沿一移动方向布置，或者在平面电动机的情形中沿两个移动方向、即在一移动平面内布置。次级部件可以沿一移动方向移动，或者在两个移动方向上的移动平面中自由移动。还可以区分短定子直线电动机和长定子直线电动机，其中在长定子直线电动机中，次级部件短于初级部件，并且在短定子直线电动机中，初级部件短于次级部件。在平面电动机的情况下，初级部件通常大于次级部件。
3.直线电动机用于电磁传输系统中，其中传输单元为了执行传输任务而移动。传输单元可被实施为次级部件或初级部件。通常，这种电磁传输系统是以长定子直线电动机或平面电动机的形式来实施的。
4.在长定子直线电动机的情况下，多个电驱动线圈沿定子固定地并排布置。在传输单元上布置有作为永磁体或者作为电线圈或短路绕组的多个驱动磁体，其通过气隙与驱动线圈分离，并且与驱动线圈相互作用。通过驱动磁体和驱动线圈的(电)磁场的相互作用，力作用于传输单元，其使该传输单元沿定子移动。在平面电动机的情况下，定子上的驱动线圈布置在一平面上。同样，在传输单元上存在布置在平面中的驱动磁体。
5.通常在各个定子段上布置有一定数量的驱动线圈。这些定子段还可具有不同的几何形状，如直线、曲线、道岔等。随后，定子段可以通过将它们串在一起来组装成所需的定子。然而，对于根据本发明的直线电动机，这种定子段的使用和这种定子段的数量是无关紧要的，定子段上驱动线圈的数量和布置也是无关紧要的。
6.通过在传输单元的驱动磁体的区域中向驱动线圈通电，可以产生与驱动磁体的磁场相互作用的磁场，以产生作用在该传输单元上的推进力(在沿定子的移动方向上或在平面电动机的情况下在沿定子的移动平面中的移动方向上)和/或法向力(在横向于移动方向的方向上)。通过控制各个驱动线圈来调节产生的磁通量，可以影响产生的力。由此，通过控制驱动线圈来产生沿移动方向移动的磁场，传输单元可以按期望的方式沿传输路径(其在平面电动机的情形中包括传输平面)移动。在此，也可以沿传输路径布置多个传输单元，其移动可以通过以下操作来单独且彼此独立地控制：通常通过施加电压来向各自与一传输单元相互作用的驱动线圈通电。
7.长定子直线电动机的示例可在wo 2013/143783 a1，us 6,876,107 b2，us 2013/0074724 a1或wo 2004/103792 a1中找到。例如，us9,202,719 b2揭示了平面电动机的基本
结构和功能。
8.为了调节传输单元的移动，通常与旋转电动机类似地使用与传输单元一起移动的dq坐标系。在平面电动机的情形中，也在两个移动方向上分开。随后，在dq坐标系中计算期望移动所需的驱动电流，其具有移动方向上的电流分量(通常也称为q分量)，并且可能具有法线方向上的电流分量(即横向于移动方向，通常也称为d分量)。在此，q分量负责产生推进力，而d分量负责产生横向于推进力的法向力。然而，对于沿定子的正常移动，通常不需要活跃的法向力(即，通过向驱动线圈通电)。随后，类似于旋转电动机，在dq坐标系中的驱动电流以逆派克变换被换算成参与力的产生的驱动线圈的线圈电流，其随后借助电力电子装置通过向驱动线圈施加相应的电压来产生。这是以为调节预先给定的时间步长(通常在1/10毫秒范围内)重复的。由于传输单元的移动，在移动期间也涉及到各种驱动线圈。这种调节不管在传输单元的两侧(在传输单元的移动方向上看到)产生力还是仅在一侧产生力。
9.例如，在khong,p.c.等人的“magnetic guidance of the mover in a long-primary linear motor(长初级直线电动机中的移动器的磁引导)”，ieee工业应用学报，卷47，第3期，2011年5月/6月，第1319-1327页中描述了基于长定子直线电动机的dq模型的这种调节。在khong中，描述了一种具有在移动方向上可见的、布置在两侧的驱动线圈的长定子直线电动机，并且在两侧上的法向力被用来使传输单元居中，以便在中间进行引导。
10.在ep 3 385 110a1中描述了一种长定子直线电动机，其中推进力和法向力彼此独立地被调节，以使得法向力能够适应传输路径的条件。在ep 3 109 998 b1中，法向力或力矩被用于控制传输单元在道岔中的移动。
11.为了调节作用在传输单元上的力和/或力矩，使用调节器、通常是由多个连续的调节器组成的调节器级联，以补偿预先给定的设定变量(例如，设定位置或设定速度)与实际变量(例如，实际位置或实际速度)之间的偏差。通常，还沿定子设有多个调节器，例如每定子段一个调节器(如ep 3 422 558 a1中所描述的)。为此，调节器根据所实现的调节规则(通常是pi调节器或pid调节器)来确定调节变量(例如，施加到驱动线圈的电压)，其随后在直线电动机上被实施。例如，调节变量由电力电子装置针对驱动线圈实施，即，产生并且施加到驱动线圈上。传统的调节器包含调节器参数，这些参数必须适应相应的调节路径，在此为具有驱动线圈的定子和具有驱动磁体及其磁耦合的传输单元，以便调整期望的调节行为，如调节误差、超调、稳定性、响应等。因此必须对调节器进行参数化，这意味着必须为调节器参数分配相应的值。这些调节器参数通常是固定的，并且在操作中不会改变。
12.ep 3 251 986 a1描述了长定子直线电动机中调节器参数的参数化。在此，还可规定，对于不同的传输单元或对于传输路径的不同位置使用不同的调节器参数集，以便能够在不同的传输单元上例如由于不同的负载、磨损状态、设计等以最佳的方式适应调节行为。为了进行参数化，利用叠加在调节变量上的激励信号对调节回路进行激励，并以频率响应的形式评估调节回路对激励的响应，从而导出调节器参数。一方面，这是复杂的，而另一方面，只能在传输路径的特定位置处且针对特定传输单元来进行。以此方式，虽然可以改进调节，但仍然缺乏灵活性。
13.本发明的任务在于，改进对直线电动机的传输单元的移动的调节、尤其是使其更加灵活。
14.该任务利用独立权利要求1的特征来解决。
15.为了尽可能精确地调节移动，质量函数包含一质量项，该质量项评估该调节的预先给定的设定变量与该调节的取决于调节变量的实际变量之间的偏差。这允许对传输单元的移动的调节的高调节质量。通过在传输单元的移动的不同移动阶段中使用不同的质量函数，可以使调节灵活地适应于相应的移动，并且在各移动阶段中实现不同的调节目标。移动阶段可以沿定子灵活配置，移动阶段中的质量函数也可以灵活配置。这并不改变对传输单元的移动的调节的基本流程，因为只有不同的质量函数被优化。
16.对传输单元的移动的基于优化的调节允许对质量函数的在线优化和离线优化。这进一步增加了对移动的调节的灵活性。
17.在离线优化的情况下，特别有利的是为各种质量函数预先创建移动特性曲线，其将移动设定变量、尤其是驱动力以及传输单元相对于有源驱动线圈的位置映射到最佳调节变量。因此，用于调节传输单元的移动的最佳调节变量必须仅从正确的特性曲线中在线读出。
18.优选地，该质量函数包括一质量项，该质量项对传输单元的移动所需的电功率进行评估。这使得有可能设有一移动阶段，在该阶段中，传输单元的移动以尽可能小的电损失功率进行。这允许直线电动机的节能操作。
19.如果质量函数包含评估调节变量之和的质量项，则可以减少用于实施调节变量的电力电子装置的各组件的热负荷和定子的加热。
20.有利的是，使用直线电动机的数学模型，利用该数学模型可以确定质量项的变量或该数学模型可用于优化的约束条件。利用该模型可以计算特定变量或参量，而不是在直线电动机中测量这些变量或参量。利用该模型还可以确定直线电动机的状态变量以及所有必要的输出变量。当使用约束条件时，确保了考虑直线电动机的物理规律，这可以普遍改进调节质量。
21.特别有利的是，利用磁阻网络(即利用由磁阻网络导出的反映物理规律的系统方程)来对直线电动机进行数学建模。利用磁阻模型可以相对于模型复杂度实现较高的系统质量(精度)。
22.在下文中将参照图1至图9更详细地阐释本发明，图1至图4示例性、示意性地而非限制地示出本发明有利的设计构造。附图中示出：
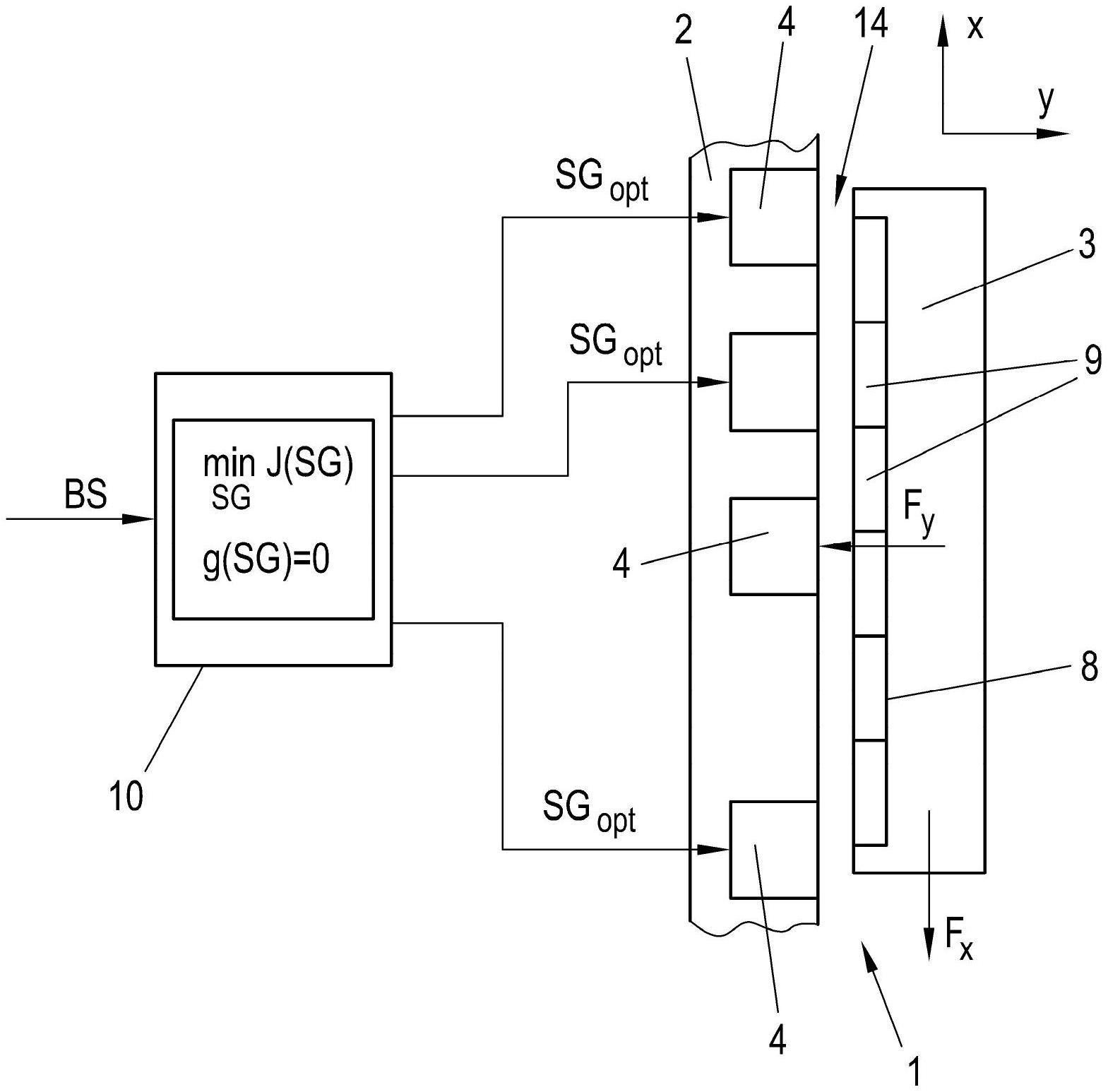
23.图1和图2示出了一种长定子直线电动机的可能结构，该长定子直线电动机具有含有带有驱动线圈的齿的定子且具有带有驱动磁体的传输单元，
24.图3和4示出了定子的磁阻网络，
25.图5示出了转子的磁阻网络及其与定子的耦合，
26.图6示出了通过优化质量函数来调节传输单元的移动
27.图7和图8示出了对传输单元的移动的调节的可能设计，以及
28.图9示出了移动特性曲线的示例。
29.本发明以作为直线电动机的实施方式的长定子直线电动机为例进行了描述，但也可以按类似的方式应用于直线电动机的其他实施方式，例如，平面电动机或短定子直线电动机。
30.在图1中，非常简化地示出了长定子直线电动机1的一示例部段。长定子直线电动机1由定子2和至少一个传输单元3组成，该传输单元3可沿定子2在移动方向x上移动。在所
示的实施例中，定子2是直线电动机的初级部件，而传输单元3是次级部件。通常，多个传输单元3(也是不同的传输单元)沿定子2同时且彼此独立地移动。定子2和传输单元3的结构设计和几何形状对本发明不重要，但当然会影响下面描述的直线电动机1模型的结构。传输单元3如何沿着定子2被引导和保持，对于本发明也不太重要。
31.在移动方向x上，多个驱动线圈4沿着定子2并排布置。驱动线圈4通常布置在由高磁导率材料(例如，铁)制成的定子齿5上，其通过定子轭6彼此相连。在具有驱动线圈4的两个定子齿5之间还可以设有不带驱动线圈4的副齿7。但副齿7也可被移除。在传输单元3上布置有具有多个驱动磁体9的驱动磁体组件8。驱动磁体组件8的在移动方向x上并排布置的驱动磁体9通常是相反极性的。驱动磁体组件8面向驱动线圈4，并通过气隙14与驱动线圈4分离。气隙14的维持通常由传输单元3在定子2上的未示出的、通常是机械的和/或磁性的引导来确保。
32.如前所述，在平面电动机的情况下，驱动线圈4布置在定子2的移动平面中。同样，驱动磁体9布置在一平面上。在平面电动机的情况下，传输单元3通常没有机械引导，但传输单元3通常保持磁性悬浮。
33.在传输单元3的驱动磁体组件8的区域中的多个驱动线圈4与驱动磁体组件8的驱动磁体9相互作用以移动传输单元3。多少驱动线圈4用于传输单元3的移动可以被假定为已知并且可以被确定，但是也可以取决于传输单元3相对于定子2的位置并且也可以取决于以下描述的优化而被确定。因此，驱动线圈4的数量也可以作为优化的结果而得知，优化藉此确定在传输单元3的环境中多少驱动线圈4应被如何通电。这些通电的驱动线圈4(以下也称为有源驱动线圈)由调节单元10调节。在传输单元3相对于定子2移动期间，驱动线圈4中的哪些驱动线圈是有源驱动线圈自然发生变化。
34.然而，应当注意的是，在驱动磁体组件8的区域中的所有驱动线圈4不一定总是有源驱动线圈。可以构想在驱动磁体组件8的区域中仅使用某些驱动线圈4作为有源驱动线圈的情况。例如，驱动线圈4可能已经发生故障，并且因此不能用于传输单元3的移动。尽管如此，传输单元3可以利用驱动磁体组件8的区域中的作为有源驱动线圈的其他驱动线圈4来移动。
35.为了避免在驱动线圈4发生故障时长定子直线电动机1发生故障，可以规定调节单元10简单地忽略故障的驱动线圈4。然而，这可能导致传输单元3的移动受到一定的干扰，但在某些情况下，例如在对传输单元3的移动没有精度要求的移动部段中，这种干扰可以忽略不计。但是，调节单元10还可以用剩余的有源驱动线圈补偿驱动线圈4的故障，以避免长定子直线电动机1的故障。为此，只需要通知调节单元10哪个驱动线圈4发生故障。这也可以在本发明的框架内非常容易地实现，如以下进一步实施的。
36.为了确定驱动线圈4的故障，可以对其施加线圈电流或线圈电压。随后，通过测量线圈电压或线圈电流，可以确定驱动线圈4是短路还是空载，这等于由于驱动线圈不再可操作而导致发生故障。这可以在长定子直线电动机1的操作中连续进行，也可以在调节传输单元3的移动期间进行。
37.驱动线圈4也可布置在沿移动方向x看过去的传输单元3的两侧上。在该情形中，传输单元3也可在沿移动方向x看过去的两侧上具有驱动磁体组件8。因此，在这样的结构中，可以在传输单元3的两侧上产生作用于传输单元3的力。然而，这并不改变以下描述的根据
本发明的调节。
38.调节单元10使用例如由设备控制单元11(例如，经由如图1所示的数据通信总线)预先给定的移动设定变量bs。设备控制单元11例如控制和监视多个传输单元3在定子2上的同时移动。在调节的通常在1/10毫秒范围内的每个时间步长中，由调节单元10根据移动设定变量bs利用在其上实现的调节(例如，以在基于处理器的硬件上运行的调节软件的形式)来确定针对涉及传输单元3的移动的多个有源驱动线圈4或每个有源驱动线圈4的调节变量sg。然而，还可以设有针对每个驱动线圈4的调节单元10。有源驱动线圈4的调节变量sg通常不相等。
39.调节变量sg可以是用于向驱动线圈4通电的线圈电流ic或线圈电压vc。线圈电流ic或线圈电压vc可以由例如ep 3 249 803 a1中描述的未示出的电力电子装置为每个涉及的驱动线圈4产生，并且可以施加到驱动线圈4上。通常，调节变量sg是施加到有源驱动线圈4的线圈电压vc。
40.在线圈电流ic作为调节变量sg的情形中，如以下进一步实施的，可以设有到线圈电压vc的换算，或者设有调节线圈电流ic的电流调节器。这可以在调节单元10中或者在电力电子装置中进行。
41.可以针对调节的每个时间步长预先给定移动设定变量bs，例如，传输单元3沿定子2的设定位置、或者设定速度或设定力。然而，移动设定变量bs也可以在调节单元10本身中确定(例如，根据沿定子2的预定移动(例如，作为传输单元3的位置或速度在时间或路径上的走向))。预定移动可以向调节单元10预先给定，但是也可以在调节单元10中被计算，例如，以便沿定子2到达预先给定的目标位置。
42.为了调节传输单元3的移动，还可以规定，例如根据沿定子2布置的已知位置传感器13(图1中所示)来确定传输单元3沿定子2的移动的实际变量(例如，实际位置)。
43.通常，在调节的每个时间步长中，从用于传输单元3的上游移动调节器中的移动设定变量bs确定必须要施加到传输单元3的驱动力和/或驱动力矩，藉此传输单元3实施期望的和预先给定的移动。移动调节器可以在调节单元10中实现，但也可以是一个独立的单元。随后从待施加的驱动力和/或驱动力矩确定针对有源驱动线圈4的调节变量sg。因此，以产生预先给定的移动所需的驱动力和/或驱动力矩的方式，向用于实施移动的有源驱动线圈4通电。
44.在此，调节单元10还可以考虑任何故障的驱动线圈4，并且确定针对有源驱动线圈4的调节变量sg，以使得在驱动磁体组件8的区域中补偿故障的驱动线圈4以实施期望的和预先给定的移动。因此，利用有源驱动线圈4而非故障线圈来产生传输单元3的移动所需的电磁场。
45.这实现了一种用于操作直线电动机1的方法，该直线电动机1具有其上布置有多个驱动线圈4的定子2，并且具有其上布置有多个驱动磁体9的沿该定子2移动的传输单元3，其中通过在该传输单元3的驱动磁体9的区域中向有源驱动线圈4通电，产生与该传输单元3的驱动磁体9相互作用以移动该传输单元3的电磁场。调节单元10确定针对有源驱动线圈4的调节变量sg、优选地线圈电流ic或线圈电压vc。根据所确定的调节变量sg来向有源驱动线圈4通电，以调节传输单元3的移动。这可以在对移动的调节的预先给定的时间步长中进行。调节单元10具有对故障的驱动线圈4的知识，或者在驱动磁体组件8的区域中自己检测故障的
驱动线圈4。为了移动传输单元3而通过剩余的有源驱动线圈4来补偿故障的驱动线圈4的作用。为此，调节单元10产生针对剩余的有源驱动线圈4的调节变量sg，从而为了移动传输单元3而补偿故障的驱动线圈4。这可以通过如下所述的优化来实现，并在专利权利要求中要求保护。
46.调节单元10和/或移动调节器可以是基于微处理器的硬件，在该硬件上实施调节软件。然而，调节单元10和/或移动调节器也可以实现为在可用的计算机硬件上安装和实施的计算机软件。然而，调节单元10和/或移动调节器也可以实施为集成电路，如专用集成电路(asic)或现场可编程门阵列(fpga)，在其上还可以实现微处理器。然而，调节单元10也可以实施为模拟电路，例如，模拟计算机。它们的组合也是可能的。
47.因此，为了调节传输单元3的移动，在调节的每个时间步长中针对每个有源驱动线圈4确定调节变量sg，即线圈电流ic或优选地线圈电压vc，藉此向有源驱动线圈4通电以产生移动所需的磁通量。
48.为了确定有源驱动线圈4的调节变量sg(例如，线圈电流ic或线圈电压vc)，使用质量函数j，该质量函数j是有源驱动线圈4的至少一个待确定的调节变量sg的函数，即j＝f(sg)，其中sg分别是具有各个涉及的有源驱动线圈4的待确定调节变量的向量。具体而言，质量函数j是数量为k个(k≥1)以加权因子kk加权的质量项jtk的和，即至少一个、优选地每个质量项jtk是有源驱动线圈4的调节变量sg的函数。优选地使用二次函数，因为其具有全局最小值，并且因此非常适合于优化。然而，质量函数j以及因此质量项jtk也可以取决于直线电动机1的其他变量，例如取决于传输单元3相对于定子2的位置、或者取决于定子2中的磁性变量(如磁通量)。
49.如果调节单元10知晓驱动线圈4是否发生故障且哪个驱动线圈4发生故障，则这可以在调节变量sg的向量中的质量函数j中考虑。藉此也将自动补偿驱动线圈4的故障。
50.调节的质量函数j(sg)被优化(最大化或最小化)(通常最小化)，以确定针对涉及的有源驱动线圈4的调节变量sg，该调节变量sg在相应的时间步长中产生以向驱动线圈4通电。优化意味着寻找那些使质量函数j(sg)最小化或最大化的调节变量sg。这些调节变量sg也称为最佳调节变量sg
opt
。
51.优化可以在线进行，即在调节的每个时间步长中进行，也可以离线进行。在离线优化的情况下，对于传输单元3的某个预先给定的移动场景(例如，作为传输单元的位置或速度在时间或路径上的时间走向)，可以预先计算在执行移动场景期间待设置的调节变量sg。为此，可以在某些时间步长中离散移动场景，并且可以在这些时间步长中的每一者中执行优化。时间步长之间也可以进行插值。由此，在传输单元3的移动的每个必要时刻、尤其是在调节的每个时间步长中存在调节变量sg。在传输系统中，由于传输单元3的移动通常是预先计划的，因此该移动场景是已知的。如果移动场景是未知的或仅部分已知的，则传输单元3的实际移动可以被延迟，以使得关于移动的充分信息再次已知。
52.在离线优化的情况下，还可以生成移动特性曲线。在传输单元3以与在移动方向上作用在传输单元3上的特定驱动力相对应的特定速度沿定子2移动的情况下，传输单元3的驱动磁体8移动经过驱动线圈4。然而，由此，这重复了待施加到有源驱动线圈4的线圈电压vc或线圈电流ic。这实现了以位置和驱动力组合的形式为特定的移动场景离线创建针对线
圈电压vc或线圈电流ic的移动特性曲线。随后，在传输单元3的移动期间，必须仅取决于移动特性曲线中的当前所需的驱动力和当前位置来读出所需的线圈电压vc和/或线圈电流ic。也可以针对不同的质量函数j(sg)创建这样的移动特性曲线。
53.在数学上，优化通常可以写成(其中如前所述，成本函数j也可以取决于调节变量sg以外的变量)。
54.优化也可以在考虑约束条件g的情况下进行。约束条件g描述了直线电动机1的物理规律。这些规律以直线电动机1的数学模型的形式表述，优选地也作为调节变量sg的函数，并且在必要时作为直线电动机1的其他变量(如状态变量)的函数。该数学模型可以是对直线电动机1的基本物理规律(例如，线圈电流ic或线圈电压uc与磁性变量(如磁通量)之间的关系)建模的模型。然而，数学模型也可以是经训练模型，例如，本地模型网络或神经网络。通常，利用该模型将直线电动机1的响应以输出变量或状态变量(通常都是向量)或两者的形式映射到输入变量(通常是向量)。输入变量通常是调节变量sg，例如，线圈电流ic或线圈电压uc。输出变量可以是例如作用在传输单元3上的驱动力(推进力和/或法向力)或驱动力矩，但也可以是传输单元3的移动变量，如沿定子2的位置、在移动方向x和/或法向y上的速度、或在移动方向x和/或法向y上的加速度。在平面电动机的情况下，驱动力可以作用在移动平面上，即，在x-z平面上。输出变量也可以是所涉及的驱动线圈4的总电流(如q或d电流)。根据运动学基本定律，驱动力/驱动力矩和移动变量是等价的，或者换言之，所得的移动变量是作用力/力矩的结果。驱动力/驱动力矩对应于总电流。描述长定子直线电动机1的状态的状态变量是例如长定子直线电动机1中由于作用的输入变量而产生的磁性变量(例如，磁通量、磁势或电压)。
55.故障的驱动线圈4也可以被表述为附加的约束条件g(例如，以“编号为xy的驱动线圈发生故障”的数学表述的形式)。例如，这可以通过针对所有驱动线圈4的向量来实现，该向量包含针对每个驱动线圈4的二进制值，其中例如“0”可以表示故障，而“1”表示无故障。
56.在数学上，考虑约束条件g的优化通常可以写成如下形式(其中如前所述，成本函数j和/或约束条件g也可以取决于调节变量sg以外的变量)。
[0057][0058]
g(sg)＝0
[0059]
为了解决这样的优化问题，存在大量已知的求解算法，仅举几例：诸如梯度法、牛顿法、进化法或逐步二次规划法。求解算法的选择对本发明无关紧要，其中当然选择在计算耗费和计算时间方面有利的这种方法(尤其是在在线优化的情况下)。求解方法的共同点是寻找优化问题的(通常是迭代的)可能的解，直到达到所定义的终止标准。例如，终止标准可以是迭代次数，或者优化问题的两个依次的迭代步骤的解之间的差值低于极限值，或者另外的终止标准。对解的选择(即，调节变量sg)在每个迭代步骤中通过求解方法的规则来进行，其中可以在第一迭代步骤中预先给定解的合适选择作为起始值。例如，在梯度法中，确定质量函数的梯度(质量函数相对于调节变量的导数)，并沿该梯度选择针对下一个迭代步骤的调节变量，其中通过求解方法的预先给定的规则来确定从当前调节变量到下一调节变量的步距。
[0060]
由于传输单元3沿定子2的移动应被调节，因此质量函数j(sg)包含质量项jtk
(sg)，该质量项评估对传输单元3的移动的调节的预先给定的移动设定变量bs与该调节的取决于调节变量sg的实际变量is、优选地移动实际变量的偏差，如以下进一步详细实施的。在此，如通常在调节的情况下，这种关系使得在调节的每个时间步长中，应以这样一种方式产生调节变量sg，即由调节变量sg引起的实际变量is应尽可能地对应于预先给定的移动设定变量bs(通常由特定的最大调节误差表示)。实际变量is通常被测量或者根据其他测得的变量来确定。
[0061]
在传输系统的直线电动机1的情况下，通常传输单元3可以沿定子2在某个路径上移动，也可以在多个经由道岔连接的路径上移动。在针对每个传输单元3的移动之前或在移动期间计划路径，这也可包括计划移动轮廓(移动变量，如在时间或路径上的速度)。还可沿路径设有加工站，在这些加工站中加工与传输单元3一起移动的对象。传输单元3也可以在沿路径移动期间输送不同的或变化的对象，例如灌装的瓶子。简言之，对传输单元3的移动的要求可以在直线电动机1沿路径的移动期间改变。
[0062]
为了能够在调节传输单元3的移动中以简单的方式表示这一点，规定在传输单元3沿路径移动的情况下存在至少两个移动阶段，其中在各移动阶段中使用不同的质量函数j(sg)。质量函数j(sg)可以通过所使用的质量项jtk(sg)的数目k和/或通过所使用的质量项jtk(sg)和/或通过加权因子kk来区分。由此，对传输单元3在不同移动阶段中的移动的调节可以根据情况灵活地适应不同的要求。甚至可以在直线电动机1的操作期间这样做。
[0063]
例如，在调节传输单元3的移动不需要特别精度的第一移动阶段中，可以寻求长定子直线电动机1的能量优化操作，而在需要精确调节移动的第二移动阶段中，可以期望对驱动力的精确调节。例如，在道岔的区域中，对传输单元3的移动的调节可以通过对法向力(在横向于移动方向x的y方向上)的调节的更高权重来进行。然而，在道岔之外，以更高的能源效率进行。
[0064]
质量项jtk(sg)评估调节的设定变量bs与调节的实际变量is的偏差，优选地作为偏差的平方，即例如jtk(sg)＝ke(bs-is(sg))2或jtk(sg)＝ke(bs-is(sg))，其中加权因子为ke。这样的质量项jtk(sg)特别可用于在线优化，其中当前实际变量is是可用的(例如通过测量)。实际变量is可以例如利用位置传感器13来测量，但也可以根据现有的已知测量变量(例如，利用观察器)来确定，其中直线电动机1的数学模型也可以作为观察器的基础。在离线优化的情况下，也可以根据直线电动机1的数学模型(即，模型的输出变量或状态变量)来确定实际变量is。由于实际变量is取决于调节变量sg，因此质量项jtk(sg)也间接取决于调节变量sg。在此，可以评估例如设定速度与实际速度的偏差、或设定位置与实际位置的偏差、或设定驱动力(或力矩)与实际驱动力(或力矩)的偏差、或设定磁通量与实际磁通量的偏差。因此，质量项jtk(sg)评估调节误差。由于位置和速度当然是施加在传输单元3上的驱动力和驱动力矩的结果，并且驱动力和驱动力矩取决于磁通量，因此上述偏差是等效的。
[0065]
在此，作用在传输单元3上的驱动力或作用的驱动力矩可以从约束条件g(sg)的数学模型中获得，其中驱动力可以是推进力(也在x-z移动平面中)和/或法向力，但也可以是z方向上的力。驱动力矩通常也可以是围绕轴x、y、z之一的力矩。驱动力和驱动力矩可以是具有不同轴x、y、z的分量的向量。随后可以从模型中计算出实际驱动力或实际驱动力矩。例如，设定驱动力或设定驱动力矩是根据调节的移动设定变量bs来确定的，或者也可以直接预先给定为设定变量。优选地，实现移动调节器，该移动调节器根据所实现的调节规则(例
如，pi或pid调节器)从移动设定变量bs和当前移动实际变量is(如实际位置或实际速度)确定所需的设定驱动力或所需的设定驱动力矩。
[0066]
另一质量项jtk(sg)可例如对传输单元3的移动所需的电功率进行评估。由于可以使用线圈电流ic或线圈电压vc作为调节变量sg，因此可以很容易地从调节变量sg确定电功率。由于可以使用线圈电流ic或线圈电压vc作为调节变量sg，因此所涉及的并且通电的有源驱动线圈4的调节变量sg(可以组合成向量)的欧几里得范数的平方被提供为评估功率的质量项jtk(sg)，即，例如其中加权因子为ki。众所周知，欧几里得范数是调节变量sg的向量的各分量的平方和的根。因此，其平方是向量的各分量的平方和。由于电功率与电流或电压的平方成正比，因此利用欧几里得范数的平方来评估实施的电功率，从而也评估能源效率。
[0067]
另一质量项jtk(sg)可以是涉及传输单元3的移动的驱动线圈4的调节变量sg的值的总和sg
σ
，也可以是和的平方，即例如jtk(sg)＝k
σ
sg
σ2
或jtk(sg)＝k
σ
sg
σ
，其中加权因子为k
σ
。由此，可以实现对调节变量的总和的评估。调节变量sg的总和越小，用于产生调节变量sg的电力电子装置的负荷就越小。这对于长定子直线电动机1的长期操作可能是有利的，因为电力电子装置的负荷尽可能均匀。由此，特别是由于较低的损耗，电力电子装置或电力电子装置中的电路组件的热负荷也可以减小。由此，还可以实现对定子2的较少加热，这也可以简化或省略对定子2的冷却。
[0068]
由此，可能的质量函数j(sg)可以定义如下。
[0069][0070]
例如，如果调节推进力f
x
和法向力fz，则质量函数j(sg)可以写成如下。
[0071][0072]
在平面电动机的情况下，驱动力fz也可以作用在z方向上，并且在质量函数j(sg)中也设有相应的质量项jtk，其中f
xs
、f
ys
、f
zs
是力的预先给定的设定值，并且f
x
(sg)、fy(sg)、fz(sg)是利用数学模型确定的力的实际值。当然，可以仅推进力fx、fz或仅法向力fy被包含在质量函数j(sg)中。以同样的方式，当然也可以考虑驱动力或驱动力矩的附加或其他分量。
[0073]
显而易见，通过改变加权因子kk(例如ki、k
σ
、ke、k
x
、ky、kz)和/或通过添加或删除某些质量项jtk(sg)(例如，可以按简单的方式来改变调节目标和调节行为。当然，除了上述的质量项之外，其他或附加的质量项jtk(sg)也是可能的。
[0074]
因此，通过根据调节变量sg(在线或离线)优化质量函数j(sg)，可以确定最小化(或最大化)质量函数j(sg)的最佳调节变量sg
opt
。这些最佳调节变量sg
opt
在直线电动机1上调节传输单元3的移动的每个时间步中被实施，如图6中示意性地示出的。例如，移动设定变量bs是针对期望的推进力f
x
、fz和法向力fy或传输单元3的待接近位置或待调整速度的预先给定。例如，通过质量项(f
xs-f
x
(sg))2,(f
ys-fy(sg))2,(f
zs-fz(sg))2,(bs-is(sg))2或驱动
力或驱动力矩的其他或附加分量来确保对该移动设定变量bs的遵循，其中该遵循的精确度可由相关的加权因子k
x
、ky、kz、ke影响。在此，其他质量项根本不需要存在，或者可以相对更低地加权。如果不要求高精度，则可以更高地加权或添加表征电功率、尤其是损失功率的质量项以实现尽可能节能的操作。由此，质量函数j(sg)在传输单元3的移动期间在不同的移动阶段中改变。具有不同质量函数j(sg)的不同移动阶段可以预先配置，或者也可以仅在移动期间(例如由设备控制单元11)确定。
[0075]
当然，通过设置进一步的质量项jtk，可以考虑直线电动机1的操作的其他方面。
[0076]
参考图6和图7，描述了在直线电动机1上或在直线电动机1的有源驱动线圈4上实施所确定的最佳调节变量sg
opt
的可能实施例。
[0077]
在根据图7的示例中，通过优化所确定的最佳调节变量sg
opt
(例如有源驱动线圈4的线圈电压vc)经由电力电子装置(未示出)直接产生并施加到驱动线圈4上。在该示例中，移动设定变量bs是传输单元3的设定位置x
set
。该设定位置x
set
也可用于优化，例如用于成本项jtk(sg)＝ke(bs-is(sg))2。为此，还可以确定(例如，测量或计算)移动变量的实际值is，在该情形中例如当前实际位置x
set
，并且在优化中使用。在移动调节器rb(在该示例中为位置调节器)中根据移动设定变量bs和移动变量的实际值is来确定驱动力f
xs
，必须调整该驱动力f
xs
以使实际值is与移动设定变量bs之间的调节误差在调节的当前时间步长中最小化。驱动力f
xs
在优化中可例如用于成本项(f
xs-f
x
(sg))2。然而，该驱动力的设定值f
xs
也可被预先给定为移动设定变量bs。在该情形中，移动调节器rb也可以与调节单元10分开实现(例如，作为具有在其上运行的软件的基于微处理器的硬件，或者作为集成或模拟电路)。在优化中，尤其是在直线电动机1的数学模型中，对于优化的约束条件g(sg)，也可以使用有源驱动线圈4的线圈电流ic的实际值，该实际值可以被测量或从其他已知值确定。调节单元10的这种实施方式特别适合于在线优化，因为在调节的每个时间步长中在直线电动机1上检测到当前实际值，例如，实际位置x和/或线圈电流ic(或线圈电压vc)的实际值。该实施方式也可用于离线优化。
[0078]
在根据图8的实施例中，所确定的最佳调节变量sg
opt
不是直接产生和实施的，而是在直线电动机1上调节的。利用优化所确定的最佳调节变量sg
opt
是例如有源驱动线圈4的最佳线圈电流i
c,opt
。这些最佳线圈电流i
c,opt
在调节单元10中用作调节变量调节器rs中的调节变量。根据最佳调节变量sg
opt
(在此为线圈电流i
c,opt
)和调节变量sg的当前实际值(在此为有源驱动线圈4的线圈电流ic)，具体而言根据其偏差，调节变量调节器rs根据所实现的调节规则(例如，pi或pid调节器)在调节的每个时间步长中确定调节变量sg(在此为有源驱动线圈4的线圈电压vc)。这些调节变量sg(在此为线圈电压vc)由电力电子装置(未示出)产生，并施加到驱动线圈4上。当然，对于有源驱动线圈4中的每一者，都存在这样的调节变量调节器rs。调节变量调节器rs可被实施为软件、基于微处理器的硬件或集成或模拟电路。然而，调节变量调节器rs也可以是电力电子装置的一部分。此外，在优化中，最佳线圈电压v
c,opt
也可被确定最佳调节变量sg
opt
。随后，这些最佳线圈电压v
c,opt
可用作调节变量调节器rs的预调，如图8中以虚线示出的。在此，最佳线圈电压v
c,opt
和利用调节变量调节器rs所确定的调节变量sg相加以得到待施加的线圈电压vc。同样，在该实施例中，类似于根据图7的实施方式，设有移动调节器rb，以便根据移动设定变量bs(例如，设定位置)来确定驱动力f
xs
。
[0079]
根据图8的调节单元10的实施方式特别适合于离线优化，但也可用于在线优化。
[0080]
在离线优化的情况下，可以使用预先创建的移动特性曲线12，其将驱动力f
x
(和/或fy、fz)和传输单元3相对于驱动线圈4的位置x映射到最佳调节变量sg
opt
，例如线圈电流i
c,opt
和/或线圈电压v
c,opt
，如以上阐释的。图9示例性地示出此类移动特性曲线12，其将传输单元3相对于多个有源驱动线圈4的位置x和驱动力f
x
映射到有源驱动线圈4的线圈电流ic。在此，当然，移动特性曲线12可用于不同定义的质量函数j(sg)，以确定不同移动阶段中的最佳调节变量sg
opt
。移动特性曲线12可以存储在调节单元10中，或者存储在外部存储单元中。为了调节传输单元3的移动，只需在正确的移动特性曲线中读出最佳调节变量sg
opt
。为此需要很少的计算能力。
[0081]
移动特性曲线12可以按表格的形式存储。随后可以在表条目之间进行插值。然而，也可以通过例如补偿计算的方法，将数学函数(例如，特定阶的多项式)匹配到移动特性曲线12中的所确定条目。在该情形中，对于移动特性曲线12，仅需要存储特定的数学函数，并且不再需要插值。
[0082]
对于其他移动方向(例如，y或z方向)，当然可以实现等效调节。
[0083]
质量项jtk(sg)的变量(例如(f
xs-f
x
(sg))2,(f
ys-fy(sg))2,(f
zs-fz(sg))2中的f
x
(sg)、fy(sg)或fz(sg))可以利用直线电动机1的数学模型来确定。在此，调节变量sg用作模型的输入变量，并且质量项jtk(sg)的变量是模型的输出变量或状态变量。
[0084]
用于优化的约束条件g(sg)和/或用于基于物理条件来确定质量项jtk(sg)的变量的直线电动机1的数学建模可以按不同的方式进行。直线电动机1的常用和充分已知的模型是dq模型或有限元(fem)模型。
[0085]
例如，dq模型在开头提及的由khong,p.c.等人描述的文档中、或在deng,z.等人的“forces and parameters of permanent magnet linear synchronous machines(永磁线性同步机的力与参数)”，ieee磁学学报，卷mag-23，第1期，1987年1月、或在boldea,i.等人的“linear electric actuators and generators(直线电执行器和发电机)”，剑桥大学出版社，1997的第4章中进行了描述。dq模型描述了dq坐标系中的电流、电压和磁通量与调节变量sg(线圈电流ic和线圈电压vc)之间的关系，并且还包括针对移动方向x(驱动力)和横向方向y(法向力)上的作用力以及其他力或力矩分量的方程。
[0086]
对直线电动机1的行为建模的另一有利的可能性是通过磁阻网络，利用该磁阻网络可以描述线圈电流ic或线圈电压vc与磁通量以及还有产生的驱动力、推进力和/或法向力以及驱动力矩之间的关系。借助磁阻网络建模的优点在于考虑了电动机变量的所有形式，而不仅仅是正弦基波。由此，非线性效应(如饱和度)以及齿槽力(cogging-force)等效应可以被系统地且以足够的抽象性建模，以使得模型也可以在线被计算。
[0087]
使用直线电动机1的磁阻网络模型来调节传输单元3的移动，即使利用与上述不同的调节方法，其本身是新颖的和创造性的。例如，磁阻网络模型可用于创建观察器，该观察器估计随后用于调节的磁通量和/或力的实际值。
[0088]
磁阻网络将直线电动机1描述为由磁阻r(磁电阻)、磁导g(磁电导)和磁电压源组成的网络。众所周知，磁阻描述了磁电压与磁通量φ之间的关系。磁导g是磁阻r的倒数。长度为l且截面为a的磁导体的磁阻r由给出，其中μ0为真空磁导率，并且μr为磁导体
材料的相对磁导率。
[0089]
利用磁阻网络的建模以作为直线电动机1的长定子直线电动机为例根据如图2所示的长定子直线电动机的结构进行了描述。在其他结构设计或其他直线电动机1的情况下(如在平面电动机的情况下)，可导致磁阻网络和模型的相应变化。
[0090]
定子2被建模为具有i＝1,
…
,n个齿(定子齿5和副齿7)的磁阻网络rn。这不一定是定子2上存在的所有齿，而是例如与传输单元3共同作用的齿。通常，选择数个驱动线圈4，这些驱动线圈4为了移动传输单元3的目的而通电。由此得到利用磁阻网络rn建模的齿数n。在j＝1,
…
,nc个定子齿5上(其中nc≤n)，布置有驱动线圈4，副齿7布置在这些驱动线圈4之间。在没有副齿7的情况下，磁阻网络rn相应地简化。定子2和传输单元3的所使用尺寸在图2中给出，并且对于直线电动机1可以假定为已知。
[0091]
每个定子齿5通过微分磁阻(每长度单位的磁阻)来建模，其中定子齿5的截面积ac＝wc·bs
。通过使用取决于磁通量φ的相对磁导率μr对材料进行非线性建模，可以考虑定子齿5的磁饱和。类似地，每个副齿7用微分磁阻来建模，其中副齿5的截面积aa＝wa·bs
。通过两个相邻齿之间具有宽度w
ca
的齿间空间的齿耦合借助微分磁导来建模。j个驱动线圈4可被建模为微分磁电压其中nc表示驱动线圈4的匝数，ls表示齿在(即横向于移动方向x的)y方向上的长度。
[0092]
随后可以用如图3所示的定子2的磁阻网络rn来对定子2在y方向上的微分部段dy进行建模。每个齿在其中形成定子的磁阻网络rn的一个分支，其中该分支由微分磁导g
‘
连接，从而构成磁阻网络rn的节点。其中，φi(y)表示第i个齿(定子齿5或副齿7)中的磁通量，而表示y方向上沿第i个齿的磁势。
[0093]
由此，在定子的磁阻网络rn的n个节点中的每一个节点上，可以建立在y方向上沿齿的磁通量φi(y)和磁势的节点和，从而得到以下2n个方程组作为系统方程。
[0094][0095]
通量和势大小的局部微分描述实现了尤其是考虑齿间空间中的不可忽视的杂散通量。
[0096]
通过用dy去除这些方程，并考虑dy
→
0，得到系统方程：
[0097][0098]
在向量φ(y)和中，n个磁通量和磁势被汇总，即φ＝[φ
1 φ2ꢀ…ꢀ
φn]
t
和系统矩阵a1和a2得到
[0099]
和a2(φ)＝diag[-r'a(φ1),-r'c(φ2),
…
,-r'a(φn)](其中diag表示对角线矩阵)，输入矩阵b得到：
[0100][0101]
为了完全建模定子2，必须将y＝ls(即，定子轭6)和y＝0(即，在去往气隙的过渡部)处的端部建模为边界条件，如图4所阐释的。两个相邻齿之间的在y＝ls处的定子轭6利用线性磁导g
sy
来建模，其中其中μ
ry
是定子轭6的假定为常数的相对磁导率，并且a
sy
＝bs·
lj是定子轭6的截面积。在y＝0的情况下，齿通过漏磁导g
s0
耦合，该漏磁导g
s0
例如可以利用来建模。线性磁导g
sy
和漏磁导g
s0
通过在定子的磁阻网络rn中构成更多的节点来再次连接定子的磁阻网络rn的分支。磁通量φ
σ
＝[φ
σ1 φ
σ2
ꢀ…ꢀ
φ
σn
]
t
表示传输单元3的驱动磁体9的流入定子2的齿的磁通量，即气隙中的磁通量。
[0102]
使用与上述相同的处理方法，再次得到作为针对y＝ls和y＝0的边界条件的方程组。
[0103]
其中矩阵其补充了系统方程。
[0104]
当定子2的齿的材料被假定为磁线性时，磁阻r’a
和r’c
对磁通量φ的依赖性消失，并且可以给出针对上述微分系统方程的解析解。
[0105]
定子2的j＝1,
…
,nc个定子齿5中的链式通量随后得到具有第i个单位向量ei的矩阵以积分选择φ(y)中属于每个定子齿5的磁通量。
[0106]
相反，如果材料是非线性的，并且发生磁饱和，则解析解是不可能的。在该情形中，可以应用近似方法来求解系统方程中的微分方程。
[0107]
例如，齿中的第i个磁通量φi和第i个磁势可以借助近似多项式gj(y)来近似，该近似多项式具有在沿齿的长度ls(在y方向上)的数量为n个支撑位置上的系数和其形式为：
[0108][0109][0110]
通过适当选择近似多项式gj(y)，可以将系统方程中的非线性微分方程组变换为可求解的非线性代数方程组。近似多项式gj(y)的一个可能选择是形式为其中j＝0,
…
,n的拉格朗日(lagrange)插值多项式。该变换是通过将近似多项式gj(y)微分到y并在n个支撑位置上求值得到的。由此根据或得到恒定的微分矩阵d。因此，矩阵d拥有条目作为系统方程的非线性代数方程组随后遵循：
[0111][0112]
其中以及经变换的系统矩阵得到其中
[0113]
和
[0114]
以及具有单位矩阵i的以及具有1＝[1 1
ꢀ…ꢀ
1]
t
和克罗内克积的
[0115]
针对边界的方程也可以按此方式进行变换，由此得到经变换的方程
[0116][0117][0118]
，其中选择矩阵为t
l
和t0，其在边界支撑点(y＝0和ls)处选择和的条目。
[0119]
由此，可以给出取决于近似磁通量的链式通量的近似，
通常可以给出为其中矩阵w由对近似多项式gj(y)和n个支撑点的选择得到。
[0120]
为了确定由传输单元3的驱动磁体9在气隙中产生的磁通量，还利用转子的磁阻网络rn
l
对气隙和传输单元3建模，如图5所阐释的。
[0121]
传输单元3通过气隙磁导g
a,ij
与定子2耦合，其索引i＝1,
…
,n表示齿数，而索引j＝1,
…
,p表示传输单元3上的驱动磁体9的数量。定子2由y＝0时定子2边缘的磁势产生的磁电压us＝[u
s,1 u
s,2
ꢀ…ꢀus,n-1
]
t
表示。利用上述近似，例如，磁电压例如由具有矩阵以及以上阐释的选择矩阵t0的得到。
[0122]
例如，驱动磁体9是由具有恒定磁电压u
msj
＝hclm(具有永磁体的厚度lm和对于所使用的永磁体已知的磁矫顽力hc)的电压源以及线性磁导描述的永磁体，其中am是永磁体的已知截面积，并且μ
rm
是永磁体的已知恒定的相对磁导率。对于其他驱动磁体9，可以使用具有非恒定的磁电压的其他模型。在传输单元3上连接驱动磁体9的磁轭利用线性磁导来描述，其具有已知的截面积a
t
和已知的恒定相对磁导率μ
rt
以及两个驱动磁体9之间的距离w
t
(例如，如图2所示的中心-中心)。传输单元3朝向定子2的一侧的漏通量通过漏磁导描述，其具有两个驱动磁体9之间的空隙的宽度w
ml
。因此，每个驱动磁体9形成具有线性磁导gm和具有磁电压源的磁电压u
msj
的转子的磁阻网络rn
l
的分支，这些分支在构成转子的磁阻网络rn
l
的节点的情况下通过气隙处的漏磁导g
ml
和磁轭处的线性磁导在各分支的末端连接。
[0123]
在气隙处的节点上连接转子的磁阻网络rn
l
的其他分支，在其中设置气隙磁导g
a,ij
。p个驱动磁体9中的每一者分别经由气隙磁导g
a,ij
与定子的磁阻网络rn中的n个所考虑的齿中的每一者连接。具有气隙磁导g
a,ij
的分支分别在构成转子的磁阻网络rn
l
的其他节点的情况下通过具有代表定子2的磁电压us的电压源连接。
[0124]
描述定子2与传输单元3之间的磁耦合的气隙磁导g
a,ij
(xs,ys)取决于传输单元3相对于定子2在移动方向x和横向方向y上的位置xs、ys。每个驱动磁体9与定子2的每个所考虑的齿磁耦合，或者，换言之，每个驱动磁体9对流入一个齿的磁通量φ
σ
做出贡献。气隙磁导g
a,ij
(xs,ys)可以假定为已知(例如，通过测量或模拟计算预先确定)。为此，仅需要确定驱动磁体9的取决于相对于定子齿5的位置xs、ys的气隙磁导g
a,ij
(xs,ys)。如果使用副齿7，则也取决于相对于副齿7的位置。例如，气隙磁导g
a,ij
(xs,ys)随后可以按表格形式、作为数学公式或作为特性曲线存储在调节单元10中。
[0125]
也可以描绘转子的磁阻网络rn
l
中两个相邻传输单元3之间的磁耦合。由此，通过该调节也将考虑到这种依赖性。
[0126]
为了从气隙和传输单元3的磁阻网络rn
l
导出独立方程的方程组，可以从不同的方式出发。一种可能的方式提供了使用众所周知的图论，如下示意性地阐释的。图论的使用是
有利的，因为其提供了用于根据自变量建立和求解方程的系统。
[0127]
转子的磁阻网络rn
l
的拓扑(图5)被分为一棵树和一棵ko树。在此，树的网络连接所有的节点，而不需要形成网(在分支上封闭的循环)，并且ko树包括所有不是树的部分的元素。对树的选择基本上是自由的，其中优选地所有磁电压源都位于树中。例如，一个合适的选择是在ko树中汇总除最后的气隙磁导g
a,np
和漏磁导g
ml
之外的所有气隙磁导g
a，ij
(xs,ys)。随后，树的磁通量φ和ko树的磁通量φc可以被汇总为向量和树元素可以被划分为具有索引ts的定子2的磁电压源，具有索引tm的驱动磁体9的磁电压源以及具有索引tg的树中的磁导。由此得到磁通量的部分向量通量的部分向量以类似的方式，得到树的磁电压u
t
和ko树的磁电压uc的向量，其中磁电压的向量并且以及树和ko树的磁通量和电压经由矩阵v以φ
t
＝vφc和uc＝-v
tut
的形式联接，其中矩阵v是由磁阻网络rn
l
的拓扑以及树和ko树的划分得到的。矩阵v可以根据上述划分以再次划分。
[0128]
矩阵v取决于定子齿元素的所选数量。
[0129]
对于nc个驱动线圈4(以及由此n＝2nc+1个齿)，矩阵vs可以表示为vs＝[v
s1
,0,v
s2
,0,v
s3
,0,v
s4
,0,v
s5
,0,0,0,0]，其中元素0描述零向量，并且v
sj
,j＝1,
…
,5是具有维数dim(v
sj
)＝(n-1)
×
(n-1)的下三角形矩阵，并且该三角矩阵的所有条目都是1。
[0130]
例如，对于五个驱动磁体8(p＝5)，矩阵vm得到vm＝[v
m1
,v
m2
,v
m3
,v
m4
,0,
…
,0,v
ml
]，其具有维数dim(v
mj
)＝p
×
n,j＝1,
…
,p-1的子矩阵。例如，这些子矩阵得到1的子矩阵。例如，这些子矩阵得到
[0131]
从树和ko树的磁通量和电压的联接中，也得到矩阵vg，其中该矩阵再次包含0、1。
[0132]
此外，磁通量φ和磁电压u还经由磁导以φ
tg
＝g
tutg
和φc＝gcuc的形式联接，其中
树的磁导矩阵为g
t
＝diag[gmꢀ…ꢀgm gbꢀ…ꢀgb g
a,np
]，并且ko树的磁导矩阵为gc＝diag[g
a,11
ꢀ…ꢀga,(n-1)p g
ml
ꢀ…ꢀgml
]。
[0133]
为了得到针对整个磁阻网络rn(rns+rn
l
)的系统方程，以上在y＝0的边界处的边界条件下的磁通量φ
σ
通过气隙中的磁通量表达，从而得到矩阵t
cφ
和t
tφ
选择n个齿中的每个齿的气隙通量，并将其相加。例如得到
[0134]
由定子的磁阻网络rn和转子的磁阻网络rn
l
得到的上述方程可以被合并，由此可以按方程组k(x)x-b(ic)＝0的形式表示整个磁阻网络rn的整个系统方程。该方程组表示直线电动机1的模型，并且可用作具有sg＝ic和状态向量x的约束条件g(sg,x)，或用于确定质量函数j(sg)的质量项jtk(sg)的变量。可以针对磁阻网络rn的任何拓扑给出该表示。
[0135]
对于根据图3、4和5的实施例，得到具有状态变量的状态向量和整个系统矩阵
[0136]
输入向量遵循
[0137]
为了得到定义良好的方程组，可以在整个系统方程中补充一行其中确定
[0138]
由此，利用该模型可计算所有系统变量、尤其是作为线圈电流ic的函数的驱动线圈4的链式磁通量ψc。整个系统方程组也可以很容易地转换，从而确定作为磁通量ψc的函数的驱动电流ic。
[0139]
通常，在直线电动机的情况下，通过借助电力电子装置产生线圈电压vc并将其施加到驱动线圈上来将线圈电压vc用作输入变量。在使用已知的电磁感应定律的情况下，利用驱动线圈4的已知欧姆电阻rc和已知电感l，可以从线圈电流ic确定线圈电压vc，反之亦然。
[0140]
根据磁阻网络rn的系统方程，例如在应用已知的磁共能原理的情况下，可以导出驱动力和/或驱动力矩，例如驱动力f
x
和轴力fy，其形式为
[0141][0142]
由此，根据传输单元3相对于定子2的相对位置[xs,ys]，可以确定作用在传输单元3上的驱动力以及驱动力矩。驱动力和驱动力矩可以补充作为直线电动机1的长定子直线电动机的模型。
[0143]
所描述的长定子直线电动机的磁阻模型当然可以扩展到作为直线电动机1的平面电动机的情形。