多时间尺度的基于荷电状态和容量的均衡策略

差异模型。
12.进一步的，所述基于所述单体最小容量-差异模型，通过双扩展卡尔曼滤波器，在多时间尺度下估计电池组中每个单体荷电状态和容量，包括：
13.基于所述单体最小容量模型，通过双扩展卡尔曼滤波器，估计mcc的荷电状态和参数，并基于所述荷电状态估计结果，通过扩展卡尔曼滤波器估计mcc的容量；
14.基于单体差异模型，通过双扩展卡尔曼滤波器，估计其他单体的δsoc和δ参数，并将所述其他单体的δsoc和所述mcc的soc共同载入容量估计ekf，得到剩余单体容量估计。
15.进一步的，所述基于每个单体的荷电状态和容量估计结果，计算每节电池需要均衡的安时积分量，并输出均衡电流，包括：
16.在未达到均衡状态时，持续输出均衡电流，直至达到均衡状态；其中，所述均衡状态为在被动均衡条件下，电池组容量等于mcc容量。
17.进一步的，所述电池组容量等于mcc容量为：
18.所述mcc可释放容量等于所有单体最小可释放容量，且所述mcc可充电容量等于所有单体最小可充电容量；
19.或电池组可释放容量或电池组可充电容量一致。
20.进一步的，所述基于一阶rc模型来建立的单体最小容量模型的状态空间方程为：
[0021][0022]ut，k
＝u
ocv，k
(sock)-u
p，k-r
o，k
(ik+i
equ，k-1
)；
[0023]
其中，k为当前执行周期，k-1为上一个执行周期，δt为执行周期时长。sock为mcc荷电状态。η为mcc库伦效率。c
k-1
为mcc的容量。ik和i
equ，k-1
分别为主回路中的电流和均衡电流，正号为放电，负号为充电。u
t，k
代表mcc端电压。r
p，k
和τk分别为极化内阻和时间常数of rc cirtuit。u
p，k
为rc电路的端电压。r
o，k
为欧姆内阻。u
ocv，k
代表ocv，ocv和soc之间的关系可以用多项式函数来拟合，具体为：
[0024]uocv
＝α1soc6+α2soc5+α3soc4+α4soc3+α5soc2+α6soc1+α7；
[0025]
其中，α1～α7为拟合系数。
[0026]
进一步的，所述基于rint模型建立的单体差异模型的状态空间方程为：
[0027]
δu
t，i，k
＝δu
ocv，i，k
(δsoc
i，k
)-δr
o，i，k
(ik+i
equ，i，k-1
)；
[0028]
其中，δu
t，i，k
代表第i节电池和mcc之间的端电压差异(正号表示大于u
t，k
，负号表示小于u
t，k
)。δu
ocv，i，k
代表第i节电池和mcc之间的ocv差异(正号表示大于u
ocv，k
，负号表示小于u
ocv，k
)。δsoc
i，k
代表第i节电池和mcc之间的soc差异(正号表示大于sock，负号表示小于sock)。δr
o，i，k
代表第i节电池和mcc之间的欧姆内阻差异(正号表示大于r
o，k
，负号表示小于r
o，k
)。
[0029]
进一步的，所述基于所述单体最小容量模型，通过双扩展卡尔曼滤波器，估计mcc的荷电状态和参数中，联合系统的非线性状态空间方程为：
[0030][0031]
容量估计的非线性状态空间方程如下：
[0032]
[ck]＝[c
k-1
]+r
c，k
[0033][0034]
其中，k为当前执行周期，k-1为上一个执行周期，δt为执行周期时长。sock为mcc荷电状态。η为mcc库伦效率。c
k-1
为mcc的容量。ik和i
equ，k-1
分别为主回路中的电流和均衡电流，正号为放电，负号为充电。u
t，k
代表mcc端电压。r
p，k
和τk分别为极化内阻和时间常数of rc cirtuit。u
p，k
为rc电路的端电压。r
o，k
为欧姆内阻。u
ocv，k
代表ocv，ocv和soc之间的关系可以用多项式函数来拟合，具体为：
[0035]uocv
＝α1soc6+α2soc5+α3soc4+α4soc3+α5soc2+α6soc1+α7；
[0036]
其中，α1～α7为拟合系数。
[0037]
进一步的，基于单体差异模型，通过双扩展卡尔曼滤波器，估计其他单体的δsoc和δ参数中，联合系统的非线性状态空间方程为：
[0038][0039][0040]
δu
t，i，k
＝δu
ocv，i，k-δr
o，i，k
(ik+i
equ，i，k-1
)+v
i，k
/e
i，k
；
[0041]
容量估计的非线性状态空间方程为：
[0042][0043][0044]
其中，k为当前执行周期，k-1为上一个执行周期，δt为执行周期时长。sock为mcc荷电状态。η为mcc库伦效率。c
k-1
为mcc的容量。ik和i
equ，k-1
分别为主回路中的电流和均衡电流，正号为放电，负号为充电。u
t，k
代表mcc端电压。r
p，k
和τk分别为极化内阻和时间常数of rc cirtuit。u
p，k
为rc电路的端电压。r
o，k
为欧姆内阻。u
ocv，k
代表ocv，ocv和soc之间的关系可以用多项式函数来拟合，具体为：
[0045]uocv
＝α1soc6+α2soc5+α3soc4+α4soc3+α5soc2+α6soc1+α7；
[0046]
其中，α1～α7为拟合系数。
[0047]
进一步的，当均衡条件为所述mcc可释放容量等于所有单体最小可释放容量，且所述mcc可充电容量等于所有单体最小可充电容量时，均衡状态的计算公式为：
[0048]cr，min，k
＝min(c
r，i，k
)&c
c，min，k
＝min(c
c，i，k
)；
[0049]
[0050]cc，i，k
＝c
c，i，k-1
+c
equ，r，i，k
[0051][0052]cequ，i，k
＝c
equ，r，i，k
+c
equ，c，i，k
；
[0053]
当所述均衡条件为电池组可释放容量或电池组可充电容量一致时，计算公式为：
[0054]cc，1，k
＝c
c，min，k
＝
…
＝c
c，n，k
；
[0055]cequ，i，k
＝max(c
c，i，k
)-c
c，i，k
；
[0056]
其中，c
r，i，k
为单体可释放容量，c
c，i，k
为单体可充电容量，c
equ，r，i，k
为单体可释放均衡容量，c
equ，c，i，k
为单体可释放均衡容量，c
equ，i，k
为总均衡容量。
[0057]
本发明采用以上技术方案，首先建立单体最小容量-差异模型；所述单体最小容量差异模型包括单体最小容量模型和单体差异模型；然后基于所述单体最小容量-差异模型，通过双扩展卡尔曼滤波器，在多时间尺度下估计电池组中每个单体荷电状态和容量；最后基于每个单体的荷电状态和容量估计结果，计算每节电池需要均衡的安时积分量，并输出均衡电流。如此，通过建立包括cmcd和cdm的mcdm模型，从而够准确描述电池组中最小容量单体mcc(minimum-capacity cell，mcc)和其他单体的动态行为，同时基于mcdm利用双扩展卡尔曼滤波器dekf，在多时间尺度上对电池组中单体soc和容量进行准确估计。解决了现有技术中，难以进行准确的容量估计，而且还必须要以准确的soc估计为前提。
[0058]
应当理解的是，以上的一般描述和后文的细节描述仅是示例性和解释性的，并不能限制本技术。
附图说明
[0059]
为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。
[0060]
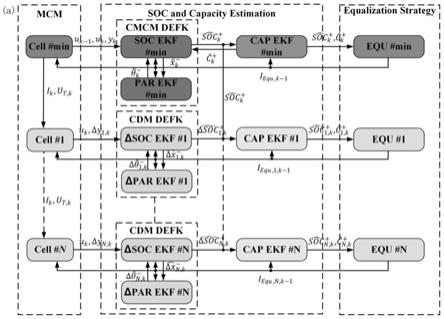
图1(a)为本技术实施例提供的用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略的算法框架图；
[0061]
图1(b)为本技术实施例提供的用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略的算法时序图；
[0062]
图2为本技术实施例提供的本技术用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略中选用的mcdm示意图；
[0063]
图3为本技术实施例提供的本技术用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略中均衡策略的示意图；
[0064]
图4为本技术实施例提供的方案中新电池组soc和容量估计图；
[0065]
图5为本技术实施例提供的方案中老电池组soc和容量估计图；
[0066]
图6为本技术实施例提供的方案中基于电压、soc和soc和容量均衡策略的电池组容量对比图；
[0067]
图7为本技术实施例提供的方案中基于电压、soc和soc和容量均衡策略的能耗对比图；
[0068]
图8为本技术实施例提供的方案中基于电压、soc和soc和容量均衡策略的首次均衡时间对比图。
具体实施方式
[0069]
这里将详细地对示例性实施例进行说明，其示例表示在附图中。下面的描述涉及附图时，除非另有表示，不同附图中的相同数字表示相同或相似的要素。以下示例性实施例中所描述的实施方式并不代表与本技术相一致的所有实施方式。相反，它们仅是与如所附权利要求书中所详述的、本技术的一些方面相一致的装置和方法的例子。
[0070]
锂离子电池单体集成电池组后，由于外部使用环境和内部特性参数的差异性，电池组的循环寿命要远低于单体的寿命。为了减少电池组的差异性，提高电池组的容量，延长循环寿命，均衡管理必不可少。被动均衡以成本低、结构简单和易控制等优点，在电动汽车和储能系统中广泛使用。与被动均衡硬件电路成熟的发展相比，高效能的均衡策略发展相对落后。
[0071]
为了解决上述问题，本技术提供一种用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略，在多时间尺度上对电池组中单体soc和容量进行估计，并给出了基于soc和容量均衡策略的执行过程。具体实现方案通过以下实施例进行详细说明。
[0072]
实施例：
[0073]
图1为本技术实施例提供的用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略，如图1(a)和图1(b)所示，在本技术实施例提供的用于被动均衡电路的多时间尺度的基于荷电状态和容量的均衡策略汇中：
[0074]
算法collective structure主要包括3个部分：第一部分即高精度高保真的多单体模型(multi-cell model，mcm)部分，用于模拟全寿命周期电池组动态、退化和均衡行为。第二部分即荷电状态(state of charge，soc)和容量估计部分，基于单体最小容量模型(cell min capacity model，cmcm)利用双扩展卡尔曼滤波器(dual extend kalman filter，dekf)(记为：cmcm dekf)估计最小容量单体soc和参数(记为：soc ekf#min和par ekf#min)，将后验soc载入容量估计ekf(记为：cap ekf#min)，获得最小容量单体容量估计。基于cdm利用dekf(记为：cdm dekf)估计其他单体(记为#i，i从#1到#n-1，不包括#min，n is cell numbers)δsoc和δ参数(记为：δsoc ekf#i和δpar ekf#i)，将后验δsoc和后验soc共同载入容量估计ekf(记为：cap ekf#i)，获得其他单体容量估计。第三部分即均衡策略部分，基于每个单体的soc和容量后验估计，计算每节电池需要均衡的安时积分量，输出均衡电流给以上各个部分(记为：equ#min和equ#i)。
[0075]
在实际应用中，为了减少算法的计算复杂度，本技术为不同的部分设计了多时间尺度的执行时序，如图1(b)所示。”sclk”主时钟周期为1s，所有部分执行周期均为主时钟周期的整数倍。mcm需要高保真模拟电池组，”cell#min+cell#i”执行周期与主时钟周期保持同步为1s。soc和容量估计部分包含cmcm和cdm部分。cmcm dekf和容量ekf是其他单体ekf的基础，”cmcm dekf+cap ekf#min”执行周期与主时钟周期保持同步为1s。cdm的差异soc和差异参数都是慢变量，因此，”cdm dekf+cap ekf#i”执行周期为(n-1)s。均衡部分需要所有单体soc和容量估计结果，”equ#min+equ#i”执行周期与”cdm dekf+cap ekf#i”周期保持同步为(n-1)s。由于容量估计需要一段时间回归，因此在前期容量回归过程中不进行均衡。
[0076]
需要说明的是，传统的串联电池组mdm is composed of a cmm and n cdms.cmm输出电压在数值上与所有单体电压的平均值对应，每次都需要计算均值，增加计算复杂度。另外，cmm没有与之对应的物理实体，缺乏明确的物理意义。借鉴mdm建模思想，所以在本技术提出mcdm，利用cmcm替换cmm，这样不仅避免平均值的计算，并且cmcm与最小容量单体形成映射关系，有明确的物理意义。此外，cdms由n个减少到n-1个。在本技术中，对比研究了基于rint、first-order和second-order的四种电池组模型。根据之前的研究结果，cmcm选为一阶rc模型，cdm选为rint模型。本技术所选用的mcdm如图2所示。
[0077]
在一些具体的实施过程中，本技术中针对cmcm模型的构建：
[0078]
由于一阶rc模型能够兼顾准度、计算复杂度和退化适应性，被广泛应用在电池管理算法中。在本技术中选择一阶rc模型装载mcdm中的cmcm，如图2(a)所示，其中，图2(a)为mcdm，图2(b)为cdm.。考虑均衡电流的cmcm状态空间方程列写如下：
[0079][0080]ut，k
＝u
ocv，k
(sock)-u
p，k-r
0，k
(ik+i
equ，k-1
).
ꢀꢀꢀꢀꢀ
(2)
[0081]
其中，k为当前执行周期，k-1为上一个执行周期，δt为执行周期时长。sock为cmc荷电状态。η为cmc库伦效率。c
k-1
为cmc的容量。ik和i
equ，k-1
分别为主回路中的电流和均衡电流，正号为放电，负号为充电。u
t，k
代表cmc端电压。r
p，k
和τk分别为极化内阻和时间常数of rc cirtuit。u
p，k
为rc电路的端电压。r
o，k
为欧姆内阻。u
oc，k1
代表ocv，ocv和soc之间的关系可以用多项式函数来拟合，列写如下：
[0082]uocv
＝α1soc6+α2soc5+α3soc4+α4soc3+α5soc2+α6soc1+α7
ꢀꢀꢀ
(3)
[0083]
其中，α1～α7为拟合系数。
[0084]
针对cdm模型的构建：
[0085]
在电池的退化过程中，ocv和欧姆内阻的变化占主导地位。另外，在本技术中，基于rint模型的cdm能够兼顾准度和计算复杂度。因此，在本技术中选择rint模型来建立cdm，如图2(b)所示。cdm的状态空间方程列写如下：
[0086]
δu
t，i，k
＝δu
ocv，i，k
(δsoc
i，k
)-δr
o，i，k
(ik+i
equ，ik-1
)
ꢀꢀꢀ
(4)
[0087]
其中，δu
t，i，k
代表第i节电池和cmc之间的端电压差异(正号表示大于u
t，k
，负号表示小于u
t，k
)。δu
ocv，i，k
代表第i节电池和cmc之间的ocv差异(正号表示大于u
ocv，k
，负号表示小于u
ocv，k
)。δsoc
i，k
代表第i节电池和cmc之间的soc差异(正号表示大于sock，负号表示小于sock)。δr
o，i，k
代表第i节电池和cmc之间的欧姆内阻差异(正号表示大于r
o，k
，负号表示小于r
o，k
)。
[0088]
建立好上述模型后，需要基于模型机芯多时间尺度的电池组soc和容量估计。首先基于cmcm模型，进行soc和参数估计：
[0089]
cmcm中的状态变量sock和u
p，k
不仅依赖于之前的短时间历史，而且随着系统控制变量的变化而迅速变化。与之相对，cmcm中的参数会随着电池老化出现缓慢变化，表明系统参数在短时间内是稳定的。在选择算法时，需要考虑电池状态与参数的变化率差异较大的
情况，最好分别进行传递和修正。因此，选择dekf算法，为建立更加独立的系统参数和状态估计路径提供了一种有效的方法。
[0090]
dekf的过程如图2所示，其中为系统的状态向量的先验估计；为系统的参数向量的先验估计，两者相互交替迭代更新。表1提供了dekf算法的细节，其由两个精心集成的ekf组成。首先，在选定cmcm模型的基础上，用dekf方法建立状态方程、参数方程和测量方程。本技术在上述过程汇中给出了cmcm的状态方程和状态量测方程，在这里状态矩阵xk＝[soc
k u
p，k
]，输入矩阵uk＝i
k-1
+i
equ，k-1
，输出矩阵yk＝u
t，k
，并增加真实系统ωk和vk噪声输入。对于参数方程，参数矩阵θk＝[r
o，k r
p，k τk]。假设两个采样点之间各参数值不变，但它们可能会随着时间的推移缓慢变化，由一个小的虚构过程噪音rk建模。参数量测方程是cmcm输出估计加上估计误差ek。联合系统的非线性状态空间方程将由公式(5)-(7)组成。
[0091][0092][0093]ut，k
＝u
oc，k-u
p，k-r
o，k
(ik+i
equ，k-1
)+vk/ekꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(7)
[0094]
在计算过程中，表1中定义的雅阁比矩阵列写如公式(8)-(12)，其中，δt为每一个执行周期。
[0095][0096][0097][0098][0099][0100]
表1基于双扩展卡尔曼滤波器的cmcm soc和参数估计
[0101][0102]
[0103]
进一步的，基于以上步骤得到结果，进行容量估计：
[0104]
虽然容量也可以作为一个电池参数放入dekf中进行估计，但是容量作为均衡策略的重要控制变量，其准度、稳定性和可靠性至关重要。因此，本技术中将容量从其他参数中剥离出来，单独进行估计。借鉴dekf中的参数估计方法，容量同样可以作为一个缓变参数进行估计。参数方程中，参数矩阵θ
c，k
＝[ck]。量测方程中，输入矩阵输出矩阵y
c，k
＝ηδt(i
k-1
+i
equ，k-1
)。容量估计的非线性状态空间方程和对应的雅阁比矩阵将由公式(13)-(15)组成。
[0105]
[ck]＝[c
k-1
|+r
c，k
[0106]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(13)
[0107][0108][0109]
然后基于cdm进行soc和容量估计。具体包括soc和参数估计和容量估计。
[0110]
对于soc和参数估计：与基于cmcm进行soc和参数估计类似，同样选择dekf来对cdm的状态和参数进行估计。表2提供了基于cdm的dekf算法的细节。首先，需要确定状态方程、参数方程和测量方程。在状态方程中，状态矩阵为δx
i，k
＝[δsoc
i，k
]。与参数估计原理类似，假设在两个执行周期单体#i与cmc的soc差异保持不变，但是随着时间的推移会缓慢变化，由一个小的虚拟噪声ω
i，k
来驱动。本技术上述过程中给出了cdm的状态量测方程，在这里输入矩阵u
i，k
＝ik+i
equ，i，k-1
，输出矩阵δy
i，k
＝δu
t，i，k
，并增加真实系统v
i，k
噪声输入。对于参数方程，参数矩阵δθ
i，k
＝|δr
o，i，k
|。假设两个采样点之间各参数值不变，但它们可能会随着时间的推移缓慢变化，由一个小的虚构过程噪音r
i，k
建模。参数量测方程是cmcm输出估计加上估计误差e
i，k
。联合系统的非线性状态空间方程将由公式(16)-(18)组成。
[0111][0112][0113]
δu
t，i，k
＝δu
ocv，i，k-δr
o，i，k
(ik+i
equ，i，k-1
)+u
i，k
/e
i，k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(18)
[0114]
在计算过程中，表2中定义的雅阁比矩阵列写如公式(19)-(22)。
[0115][0116][0117]
[0118][0119]
表2基于双扩展卡尔曼滤波器的cdm soc和参数估计
[0120]
[0121][0122]
对于容量估计：
[0123]
借鉴基于cmcm进行容量估计。在cdm中，容量同样可以作为一个缓变参数进行估计。参数方程中，参数矩阵量测方程中，输入矩阵可以分解为输出矩阵y
c，i，k
＝ηδt(i
k-1
+i
equ，i，k-1
)。容量估计的非线性状态空间方程和对应的雅阁比矩阵将由公式(23)-(26)组成。
[0124][0125][0126]
[0127][0128]
进一步的，在准确估计各单体soc和容量的基础上，本技术进一步设计基于soc和容量的均衡策略。本技术选择被动均衡电路，后面的讨论均在被动均衡的前提下。例如选择3节不同容量不同初始soc的单体为例来阐述这个过程，这3节电池标号依次为#1～#3，总容量依次为90ah，95ah，100ah，如图3所示，其中，图3为基于soc和容量的均衡策略，图3(a)均衡前c
t，pack，k
＜c
t，min，k
，图3(b)均衡后c
r，min，k
＝min(c
r，i，k
)&c
c，min，k
＝min(c
c，i，k
)，图3(c)均衡后c
c，1，k
＝c
c，min，k
＝...＝c
c，n，k
。在均衡前，3节电池初始soc分别为88.89％，78.95％，95％。根据公式(27)-(28)，计算出单体可释放容量c
r，i，k
分别为80ah，75ah，95ah，单体可充电容量c
c，i，k
分别为]0ah，20ah，5ah。根据公式(29)-(31)，计算出电池组可释放容量c
r，pack，k
，电池组可充电容量c
c，pack，k
和电池组总容量c
t，pack，k
分为75ah，5ah和80ah，如图3(a)所示。在被动均衡条件下，电池组容量小于cmc容量，表明电池组并未处于均衡状态，需要进一步进行均衡。
[0129]cr，i，k
＝c
t，i，k
*soc
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(27)
[0130]cc，i，k
＝c
t，i，k
*(1-soc)
ꢀꢀꢀꢀꢀꢀꢀꢀ
(28)
[0131]cr，pack，k
＝min(c
r，i，k
)
[0132]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(29)
[0133]cc，pack，k
＝min(c
c，i，k
)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(30)
[0134]ct，pack，k
＝c
r，pack，k
+c
c，pack，k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(31)
[0135]
在被动均衡条件下，电池组容量等于cmc容量即为达到均衡状态。这需要同时满足两个条件：1.cmc可释放容量等于所有单体最小可释放容量；2.cmc可充电容量等于所有单体最小可充电容量，如公式(32)所示。进一步，需要计算各单体所需要的均衡容量。根据条件1，各单体可释放均衡容量的计算公式如(33)所示。根据条件2，各单体可充电均衡容量的计算公式如(34)-(35)所示。各单体总均衡容量为可释放均衡容量和可充电均衡容量的和，计算公式如(36)所示。以3节样本电池为例，各单体可释放均衡容量c
equ，r，i，k
分别为5ah，0ah，0ah，各单体可释放均衡容量c
equ，c，i，k
分别为0ah，0ah，10ah，总均衡容量c
equ，i，k
分别为5ah，0ah，10ah。均衡后如图3(b)所示，电池组可释放容量75ah等于cmc可释放容量75ah，电池组可充电容量15ah等于cmc可充电容量15ah，电池组总容量90ah等于cmc总容量90ah。实现了被动均衡条件下电池组的均衡状态。
[0136]cr，min，k
＝min(c
r，i，k
)&c
c，min，k
＝min(c
c，i，k
)
ꢀꢀꢀꢀꢀꢀꢀ
(32)
[0137][0138]cc，i，k
＝c
c，i，k-1
+c
equ，r，i，k
ꢀꢀꢀꢀꢀꢀꢀꢀ
(34)
[0139][0140]cequ，i，k
＝c
equ，r，i，k
+c
equ，c，i，k
ꢀꢀꢀꢀꢀꢀꢀꢀ
(36)
[0141]
从图3(b)可以看出，电池组各单体不论是可释放容量还是可充电容量都没有达到一致，这是一种宽约束的均衡策略，并且计算过程相对复杂。然而，工程实践中通常采用以上均衡策略的一个特例，即可释放容量或可充电容量一致。以可充电容量一致为例说明，可释放容量一致过程类似，不再赘述。各单体可充电容量一致判断条件如(37)所示，均衡容量计算公式如(38)所示。同样，以3节样本为例，可充电容量c
c，i，k
分别为10ah，20ah，5ah，均衡容量c
equ，i，k
分别为10ah，0ah，15ah，如图3(c)所示。虽然，相比前面的均衡策略，首次均衡消耗的电量会大一些，但是计算复杂度会降低，因此本技术的方案中采用后者。
[0142]cc，1，k
＝c
c，min，k
＝...＝c
c，n，k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(37)
[0143]cequ，i，k
＝max(c
c，i，k
)-c
c，i，k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(38)
[0144]
本技术提供一种本文提出基于多时间尺度的电池组soc和容量估计的被动均衡策略。首先，建立了单体最小容量-差异模型，该模型包括单体最小容量模型和单体差异模型，能够准确描述电池组中最小容量单体和其他所有单体的动态行为。其次，基于mcdm利用双扩展卡尔曼滤波器，在多时间尺度上对电池组中单体soc和容量进行估计，并给出了基于soc和容量均衡策略的执行过程。兼顾电池组容量最大化、均衡能耗最小化和首次均衡时间最小化指标，实现全寿命周期高效能均衡。
[0145]
下面将以仿真实验的方式，对本技术提供的方案进行验证。对电池组进行全寿命周期的实验验证存在巨大挑战，包括：单体数量多、实验时间长和实验数据大，这些都不利于原理阶段的验证。另外，实验验证难以得到单体准确的soc和容量，这会带来估计算法缺少基准值。因此，下面将通过仿真的手段验证所提出的估计算法和均衡策略。
[0146]
首先进行实验设计：为了高保真的模拟电池组全寿命周期的动态行为，我们采用基于1阶rc的mcm。在仿真工况中，采用动态压力测试(dynamic stress test，dst)作为放电工况，放电至电池组中单体最低电压达到下限截止电压或最低soc达到0％。采用1c恒流充电作为充电工况，充电至电池组中单体最高电压达到上限截止电压或最高soc达到100％。为了保证模拟的逼真性，模型参数的设置以真实电池组全寿命周期退化过程参数为指导。电池组由四个串联的电池组成，电池带有一个锂(ni0.8co0.1mn0.1)氧阴极和一个石墨阳极。每个电池的额定容量和电压分别为177ah和3.61v。上限和下限截止电压分别为4.2和2.8v。.该电池组经历大约700次循环，cmc的容量达到寿命截止条件，即：初始容量的80％。在真实电池组参数的指导下，仿真mcm参数设置如下：
[0147]
初始soc：正态随机给定，均值93.5％，方差1.3％；平均值：93.5％，最大值95％，最小值92％，差异：3.16％。
[0148]
初始容量c
t，i，1
：正态随机给定，均值177ah，方差2ah；平均值：176.923ah，最大值180.186ah，最小值173.843ah，差异：3.52％。
[0149]
容量退化率c
loss，i，k
：本文的容量衰减模型采用wang等提出的经验模型[19]，其公式为：
[0150]closs
＝kcah
0.55
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(39)
[0151]
其中，kc为容量衰减系数，仿真实验中服从正态分布。电池组进行700次循环，容量损失大约为20％，对应衰减系数均值为0.0413。容量衰减通常无法筛选，因此方差给定较大为0.005。最大kc为0.0448，最小kc为0.0378，均值为0.0412，约有15.55％差异。
[0152]
初始欧姆电阻r
o，i，1
：真实电池组初始欧姆电阻均值为0.349mω，方差为0.005mω。
在仿真实验中给定正态分布，均值、方差与真实值相同。初始欧姆电阻，最大值为0.354mω，最小值为0.336，差异为5.07％。
[0153]
欧姆电阻退化率r
loss，i，k
：本文的欧姆内阻增长模型采用matsushima等提出的线性经验模型，其公式为：
[0154]rloss
＝krah
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(40)
[0155]
其中，ks为欧姆内阻增长系数。仿真实验中欧姆内阻增长系数大小与容量衰减系数大小相关，最大kr为0.0448，最小kr为0.0378，均值为0.0412，约有15.55％差异。
[0156]
极化电阻r
p，i
：4节单体电池极化电阻仿真实验与初始真实值相同，并且全寿命周期保持不变。
[0157]
时间常数τi：4节单体电池时间常数仿真实验与初始真实值相同，并且全寿命周期保持不变。
[0158]
库伦效率ηi：4节单体电池库伦效率真实值非常接近1。在仿真实验中给定正态分布，均值为0.9995，方差为0.0001。4节单体的仿真库伦效率，最大值为0.99967％，最小值为0.99930％，差异为0.04％，在全寿命周期保持不变。
[0159]
均衡电流：4节单体电池的均衡电流均为100ma，并且全寿命周期保持不变。电池组仿真模型参数如表3所示。
[0160]
表3电池组仿真模型参数表
[0161][0162][0163]
需要说明的是，实验大纲包括两个部分：电池组soc和容量估计和均衡性能。第1部分电池组soc和容量估计利用第1次循环的新电池组和第672次循环(倒数第2次循环，最后1次循环不完整)的老电池组soc和容量仿真数据作为参考值，对多时间尺度电池组soc和容量估计算法进行验证。
[0164]
第2部分均衡性能利用全寿命周期电池组容量、均衡能耗和首次均衡时间性能指标，对基于电压、基于soc和基于soc和容量的3种均衡策略进行综合的比较分析。为了使每种均衡策略都能尽可能实现均衡变量的一致性，均衡截止阈值设置尽可能小，以避免其带来的均衡性能下降。完整的均衡性能试验大纲如表4所示，其中，图4为新电池组soc和容量估计。图4(a)为新单体soc估计曲线，图4(b)为新单体soc估计误差曲线，图4(c)为新单体容量估计曲线，图4(d)为新单体容量估计误差曲线。
[0165]
表4均衡性能试验大纲和对比性能
[0166]
[0167]
在完成仿真实验设计后，进行获取以及分析电池组soc和容量估计结果。
[0168]
具体的，第1次循环的新电池组的soc和容量估计结果如图4所示，第672次循环的老电池组的估计结果如图5所示。图4(a)，(b)，图5(a)，(b)分别为单体soc估计曲线和误差曲线。图4(c)，(d)，图5(c)，(d)分别为单体容量估计曲线和误差曲线。在本文中”cell#1～#4real”是由mcm生成的真实值，”cell#1～#4estimation”是由多时间尺度电池组soc和容量估计值，“cell#1～4error”是由真实值与估计值的差值得到。新电池组和老电池组估计的soc和容量的rmse如表5所示。
[0169]
如图4所示，给出了新电池组的单体soc和容量估计结果。从图4(a)的单体soc估计结果，可以看出多时间尺度估计方法能够在全soc范围提供准确的soc估计。从子图能够看出算法的回归速度很快，在10s以内算法回归到真值。图4(b)展示了单体soc估计误差曲线。从结果可以看出本文所提出的方法可以保持soc估计误差在0.015％以内。从图4(c)的单体容量估计结果，可以看出所提出方法能够在4000s左右回归到真值，从此之后一直紧紧跟随真值。图4(d)展示了单体容量估计误差曲线。从结果可以看出本文所提出的方法可以保持容量估计误差在6ah(3.39％full seale)以内。
[0170]
图5为老电池组soc和容量估计。图5(a)为老单体soc估计曲线；土5(b)为老单体soc估计误差曲线；土5(c)为老单体容量估计曲线；土5(d)为老单体容量估计误差曲线。如图5所示，给出了老电池组的单体soc和容量估计结果。从图5(a)的单体soc估计结果，可以看出所提出的方法同样能够在全soc范围提供准确的soc估计，并且能够在10s内回归到真值。图5(b)展示了单体soc估计误差曲线。从结果可以看出本文所提出的方法同样可以保持soc估计误差在0.015％以内。与新电池组估计结果相近。从图5(c)的单体容量估计结果，可以看出所提出方法同样能够在4000s左右回归到真值，从此之后一直紧紧跟随真值。图5(d)展示了单体容量估计误差曲线。从结果可以看出本文所提出的方法可以保持容量估计误差在4ah(2.84％full scale)以内。这个结果比新电池组的估计结果准度高。
[0171]
表5列出了新电池组和老电池组的单体soc和容量估计的rmse值。新电池组单体soc估计的最大rmse为2.3775e-6％，平均rmse为2.1924e-6％。老电池组单体soc估计的最大rmse为2.7529e-6％，平均rmse为2.3547e-6％，两者估计准度都很高，并且相差无几。新电池组单体容量估计的最大rmse为0.1617ah，平均rmse为0.1471ah。老电池组单体容量估计的最大rmse为0.1099ah，平均rmse为0.1059ah。两者估计准度都很高，老电池组略高于新电池组，这主要由于老电池组容量差异性更小。因此，我们可以得出以下结论，本文所提出的方法在新电池组和老电池组上准度都很高，它能够在全寿命周期准确有效地估计每个单体的soc和容量。
[0172]
表5 rmse of new and aged battery cell soc(％)and capacity(ah)estimations.
[0173]
[0174]
紧接着，对均衡性能机芯分析，包括：
[0175]
对于电池容量：基于电压、基于soc和基于soc和容量的均衡策略全寿命周期电池组容量对比结果如图6所示。图6(a)为基于电压的均衡策略电池组容量。图6(b)为基于soc的均衡策略电池组容量。图6(c)为基于soc和容量的均衡策略电池组容量。图6(d)为3种均衡策略电池组容量对比。在本文中”cell#1～#4”是由mcm生成的真实值单体容量，”pack theory”是被动均衡下电池组容量理论值，其数值上等于最小单体容量，“pack real”是由3种均衡策略均衡后得到真实容量，“cycle”为电池组循环数。
[0176]
从图6(a)(b)(c)的电池组容量结果，可以看出基于电压、基于soc和基于soc和容量的3种均衡策略均能够快速回归到电池组容量理论值，并且在全寿命周期紧紧跟随理论值。从图6(d)的电池组容量对比结果，可以看出3种均衡策略的电池组理论值和真实值都达到了标称容量177ah的80％，即为141.6ah。然而，3种均衡策略的全寿命周期的循环次数分别为670，665和673次，基于电压和soc的均衡策略循环次数小于基于soc和容量的均衡策略循环次数，这主要由于前两种均衡策略的均衡能耗大，在全寿命周期中比基于soc和容量的均衡策略放电量多，导致电池组加速退化，这将在下面详细分析。
[0177]
对于均衡能耗：基于电压、基于soc和基于soc和容量的均衡策略全寿命周期均衡能耗对比结果如图7所示。图7(a)为基于电压的均衡策略均衡能耗。图7(b)为基于soc的均衡策略均衡能耗。图7(c)为基于soc和容量的均衡策略均衡能耗。图7(d)为3种均衡策略均衡能耗对比。在本文中”cell#1～#4”是每个单体的均衡能耗，”sum”是所有单体均衡能耗的和。
[0178]
从图6(a)(b)的均衡能耗结果，可以看出基于电压和基于soc的2种均衡策略在全寿命周期中所有单体均在不停进行均衡。然而，从图6(c)的均衡能耗结果，可以看出基于soc和容量的均衡策略在cell#4达到均衡截止阈值条件后就不再进行均衡。从图6(d)的均衡能耗对比结果，可以看出不论是单体均衡能耗还是均衡能耗和，基于soc的均衡能耗最大，总能耗为3435.32wh。基于电压的均衡能耗次之，总能耗为1055.41wh。基于soc和容量的均衡能耗最小，总能耗为381.64wh。另外，每个单体的均衡能耗与库伦效率相关。通过均衡能耗的对比分析，可以看出基于电压和基于soc的均衡策略会经常出现过均衡的问题。然而，基于soc和容量的均衡策略能够有效避免过均衡的问题。
[0179]
对于首次均衡时间：基于电压、基于soc和基于soc和容量的均衡策略首次均衡时间对比结果如图8所示。图8(a)为基于电压的均衡策略首次均衡时间。图8(b)为基于soc的均衡策略首次均衡时间。图8(c)为基于soc和容量的均衡策略首次均衡时间。图8(d)为3种均衡策略首次均衡时间对比。在本文中”cell#1～#4”是由mcm生成的真实值单体容量，”pack theory”是被动均衡下电池组容量理论值，其数值上等于最小单体容量，“pack real”是由3种均衡策略均衡后得到真实容量，“time”为首次均衡时间，“cycle”为电池组循环数。
[0180]
从图8(a)(b)(c)的首次均衡时间结果，可以看出基于电压、基于soc和基于soc和容量的3种均衡策略均能够逐步回归到电池组容量理论值。从图8(d)的首次均衡时间对比结果，可以看出基于电压的首次均衡时间最长，时间为192856s，循环数为6。基于soc的首次均衡时间次之，时间为118890s，循环数为3。基于soc和容量的首次均衡时间最短，时间为114022s，循环数为3。通过首次均衡时间的对比分析，可以看出基于电压的均衡策略会经常出现均衡间隙，这主要由于小电流条件下单体压差无法触发均衡阈值。然而，基于soc和soc
和容量的均衡策略能够准确表达不一致性，有效避免均衡间隙的问题。
[0181]
综上所述，将基于电压、soc和soc和容量均衡策略的均衡性能对比整理列写如表6所示。基于电压的均衡策略的电池组实际容量接近理论容量，循环数处于中等水平；单体和总能耗也处于中等水平；首次均衡时间和循环数处于低水平。基于soc的均衡策略的电池组实际容量和理论容量保持一致，循环数处于低水平；单体和总能耗也处于低水平；首次均衡时间和循环数处于高水平。基于soc和容量的均衡策略的电池组实际容量和理论容量保持一致，循环数处于高水平；单体和总能耗处于高水平；首次均衡时间和循环数也处于高水平。我们可以得出以下结论：传统的基于电压和soc的均衡策略无法同时兼顾电池组容量、均衡能耗和首次均衡时间性能。然而，基于soc和容量的均衡策略则能够兼顾电池组容量最大化、均衡能耗和首次均衡时间最小化性能，实现全寿命周期高效能均衡策略。
[0182]
基于电压、soc和soc和容量3种均衡策略对于计算资源的要求依次从低到高，如果针对一些计算资源和成本比较敏感的场景，推荐采用基于电压的均衡策略，能够兼顾成本和部分性能。另外，也可以考虑采用基于电压和soc结合的均衡策略，当电池组一致性较差时，用基于soc的均衡策略使电池组容量快速回归；当电池组一致性较好时，用基于电压的均衡策略降低均衡能耗。以上场景对均衡硬件电路的散热性能要求较高。如果针对计算资源和成本不敏感，注重均衡性能的场景，推荐采用基于soc和容量的均衡策略。该场景对均衡硬件电路的散热性能要求较低。
[0183]
表6基于电压、soc和soc和容量均衡策略的均衡性能对比
[0184][0185]
针对电池组使用过程中参数差异性逐渐增加的问题，本技术提出一种基于多时间尺度的电池组soc和容量估计的被动均衡策略。首先，建立了mcdm，该模型包括cmcd和cdm，能够准确描述电池组中最小容量单体和其他单体的动态行为。其次，基于mcdm利用双扩展卡尔曼滤波器dekf，在多时间尺度上对电池组中单体soc和容量进行估计。基于此提出了基于soc和容量均衡策略。最后，利用高保真的mcm，在实际电池组退化数据的指导下，对所提出的均衡策略进行全寿命周期的仿真验证。实验结果表明，所提出方法能够在新和老电池组上高效准确地估计单体soc和容量，实现全寿命周期高准度估计。相比于传统的基于工作电压和soc的均衡策略，所提出的均衡策略能够兼顾电池组容量最大化、均衡能耗最小化和均衡时间最小化指标，实现全寿命周期高效能均衡。
[0186]
可以理解的是，上述各实施例中相同或相似部分可以相互参考，在一些实施例中未详细说明的内容可以参见其他实施例中相同或相似的内容。
[0187]
需要说明的是，在本技术的描述中，术语“第一”、“第二”等仅用于描述目的，而不能理解为指示或暗示相对重要性。此外，在本技术的描述中，除非另有说明，“多个”的含义
是指至少两个。
[0188]
流程图中或在此以其他方式描述的任何过程或方法描述可以被理解为，表示包括一个或更多个用于实现特定逻辑功能或过程的步骤的可执行指令的代码的模块、片段或部分，并且本技术的优选实施方式的范围包括另外的实现，其中可以不按所示出或讨论的顺序，包括根据所涉及的功能按基本同时的方式或按相反的顺序，来执行功能，这应被本技术的实施例所属技术领域的技术人员所理解。
[0189]
应当理解，本技术的各部分可以用硬件、软件、固件或它们的组合来实现。在上述实施方式中，多个步骤或方法可以用存储在存储器中且由合适的指令执行系统执行的软件或固件来实现。例如，如果用硬件来实现，和在另一实施方式中一样，可用本领域公知的下列技术中的任一项或他们的组合来实现：具有用于对数据信号实现逻辑功能的逻辑门电路的离散逻辑电路，具有合适的组合逻辑门电路的专用集成电路，可编程门阵列(pga)，现场可编程门阵列(fpga)等。
[0190]
本技术领域的普通技术人员可以理解实现上述实施例方法携带的全部或部分步骤是可以通过程序来指令相关的硬件完成，所述的程序可以存储于一种计算机可读存储介质中，该程序在执行时，包括方法实施例的步骤之一或其组合。
[0191]
此外，在本技术各个实施例中的各功能单元可以集成在一个处理模块中，也可以是各个单元单独物理存在，也可以两个或两个以上单元集成在一个模块中。上述集成的模块既可以采用硬件的形式实现，也可以采用软件功能模块的形式实现。所述集成的模块如果以软件功能模块的形式实现并作为独立的产品销售或使用时，也可以存储在一个计算机可读取存储介质中。
[0192]
上述提到的存储介质可以是只读存储器，磁盘或光盘等。
[0193]
在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本技术的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不一定指的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任何的一个或多个实施例或示例中以合适的方式结合。
[0194]
尽管上面已经示出和描述了本技术的实施例，可以理解的是，上述实施例是示例性的，不能理解为对本技术的限制，本领域的普通技术人员在本技术的范围内可以对上述实施例进行变化、修改、替换和变型。