一种基于仿射的不确定性模态分析方法

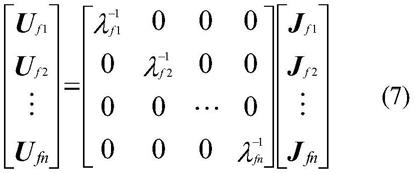
1.本发明属于风电技术领域，具体涉及一种基于仿射的不确定性模态分析方法。


背景技术：

2.随着化石能源的枯竭以及环境的不断恶化，以风电为代表的新能源得到了广泛应用。在风电场的并网过程中存在许多并网电能质量问题，其中，谐波谐振现象所造成的影响尤为明显。谐波谐振会造成风电场中某次谐波幅值突然抬升，形成过电压或过电流，导致风电场中保护误动、设备受损等问题。由于风力发电存在较大的不确定性，风电并网系统输出功率的变化会使得并联补偿电容器的投入与切出成为动态变化的过程，这一过程中风电场的谐振点会随着外界条件的变化而转移。采用能够获取风电并网谐波谐振动态信息的模态分析方法，是分析不确定性对谐波谐振影响的关键。
3.由于传统的模态分析法只能对系统的谐波谐振进行确定性分析，所以目前谐波谐振的相关研究多为确定性分析，尚未考虑不确定变量对新能源并网系统的不确定性影响。为有效调整并网系统的谐振频率以治理谐波谐振现象，需要进一步分析系统参数的不确定性所引起的系统谐振的不确定性变化情况。


技术实现要素：

4.本发明的目的在于提供一种基于仿射的不确定性模态分析方法，该方法有利于抑制风电场并网系统谐振。
5.为实现上述目的，本发明采用的技术方案是：一种基于仿射的不确定性模态分析方法，包括以下步骤：
6.(1)将无功补偿装置svc的补偿容量表示成复仿射形式求得svc对风电场并网系统产生的节点导纳表达式
7.(2)计算出在频率f处的并网系统节点导纳矩阵yf，对其进行特征值分解，对特征值矩阵λ求逆得到模态阻抗矩阵λ-1
；
8.(3)建立仿射量与并网系统谐波次数、并网系统模态阻抗的关联曲面图，得到不同svc补偿容量下的模态阻抗曲线及任一谐振模式下各偶数次谐振频率所对应的区间。
9.进一步地，所述步骤(1)中，对于接入无功补偿装置svc的风电场并网系统，当无功补偿装置svc的补偿容量发生变化时，风电场并网系统的谐振频率随之产生变化；构造svc的补偿容量复仿射表达式如下：
[0010][0011]
其中，q
svc,0
为单个无功补偿装置svc的仿射中心值；qi由svc的额定容量决定，在复
仿射表达式中为噪声元系数；εi表示svc的无功输出波动范围，取值为εi∈[-1,1]；
[0012]
基于复仿射形式的svc的补偿容量计算svc对风电场并网系统产生的节点导纳表达式如下：
[0013][0014]
式中，vb为svc的额定电压，h为谐波次数。
[0015]
进一步地，所述步骤(2)中，模态阻抗的计算方法为：
[0016]
在频率f处接入svc的风电场并网系统节点导纳矩阵yf：
[0017][0018]
若系统产生频率为f的并联谐振现象，其节点电压、电流方程为：
[0019][0020]
其中，yf为在频率f处的并网系统节点导纳矩阵，vf和if分别为节点电压和节点注入电流向量；节点导纳矩阵yf分解如下：
[0021]
yf＝lλt
ꢀꢀꢀ
(5)
[0022]
式中，λ为对角特征值矩阵，λ＝diag(λ1,λ2,
…
λk,
…
)；l＝[l1,l2,
…
lk,
…
]、t＝[t1,t2,
…
tk,
…
]分别为左、右特征向量矩阵，且有l＝t-1
；
[0023]
将式(5)代入式(4)得到：
[0024]vf
＝lλ-1
tifꢀꢀꢀ
(6)
[0025]
定义uf＝tvf为模态电压向量，jf＝tif为模态电流向量，则有uf＝λ-1
jf；即：
[0026][0027]
式中，λ-1
为模态阻抗矩阵。
[0028]
进一步地，采用所述模态分析方法分析并网谐振不确定性的具体步骤如下：
[0029]
1)基于模态分析模型，根据式(1)计算得到svc补偿容量复仿射表达式再根据式(2)计算得到节点导纳复仿射表达式
[0030]
2)计算得到系统节点导纳矩阵y(s)；
[0031]
3)对节点导纳矩阵y(s)进行特征值分解，即y(s)＝l(s)λ(s)t(s)，从而得到左、右特征向量矩阵l(s)、t(s)及对角特征值矩阵λ(s)；
[0032]
4)计算系统频率为f时各模式下的模态阻抗；
[0033]
5)重复步骤2)-4)，直至遍历所有可能引起系统谐振的谐波频率，从而得到各谐波
频率下的系统模态阻抗曲线图，进而分析风电场并网谐振现象；结合svc的仿射模型与节点导纳复仿射表达式，得到各谐波频率下的系统模态阻抗曲线，进而获取svc补偿容量与系统谐振频率的关联曲线。
[0034]
进一步地，所述步骤(3)中，对风电并网系统进行模态分析，建立仿射量与并网系统谐波次数、并网系统模态阻抗的关联曲面图；通过分析模态阻抗最大值所在位置，确认不同下的并网系统谐振频率，建立svc补偿容量与并网系统谐振频率的关联曲线；并网系统谐振频率与svc补偿容量存在正相关的关系，基于此规律，通过分析如何调节大小，实现谐振频率的调整；由于实际电力系统中几乎不存在偶次谐波，调节并网系统谐振频率至偶数次，以达到抑制风电场并网系统谐振的目的。
[0035]
与现有技术相比，本发明具有以下有益效果：本发明基于仿射运算，充分考虑风电场参数不确定性，对svc的补偿容量、并网系统谐振频率与并网系统模态阻抗的关联进行研究分析，获取svc无功补偿容量与风电场并网系统谐振频率的关联曲线，以及某一谐振模式下各偶数次谐振频率所对应的区间。据此能够分析如何调节无功补偿容量大小，将谐振频带有效地移至目标频带(偶数次谐波)，达到抑制风电场并网系统谐振的目的。本发明不仅能够用于分析参数不确定性对系统谐振频率的影响，还能够为谐波谐振治理提供依据，且治理方法无需引入新的滤波装置，不会产生额外的谐振频率。
附图说明
[0036]
图1是本发明实施例的方法实现流程图；
[0037]
图2是本发明实施例中不同svc补偿容量下的模态阻抗曲线图；
[0038]
图3是本发明实施例中svc补偿容量与并网系统谐振频率的关联曲线图。
具体实施方式
[0039]
下面结合附图及实施例对本发明做进一步说明。
[0040]
应该指出，以下详细说明都是示例性的，旨在对本技术提供进一步的说明。除非另有指明，本文使用的所有技术和科学术语具有与本技术所属技术领域的普通技术人员通常理解的相同含义。
[0041]
需要注意的是，这里所使用的术语仅是为了描述具体实施方式，而非意图限制根据本技术的示例性实施方式。如在这里所使用的，除非上下文另外明确指出，否则单数形式也意图包括复数形式，此外，还应当理解的是，当在本说明书中使用术语“包含”和/或“包括”时，其指明存在特征、步骤、操作、器件、组件和/或它们的组合。
[0042]
如图1所示，本实施例提供了一种基于仿射的不确定性模态分析方法，包括以下步骤：
[0043]
(1)将无功补偿装置svc的补偿容量表示成复仿射形式求得svc对风电场并网系统产生的节点导纳表达式
[0044]
(2)计算出在频率f处的并网系统节点导纳矩阵yf，对其进行特征值分解，对特征
值矩阵λ求逆得到模态阻抗矩阵λ-1
。
[0045]
(3)建立仿射量与并网系统谐波次数、并网系统模态阻抗的关联曲面图，得到不同svc补偿容量下的模态阻抗曲线及任一谐振模式下各偶数次谐振频率所对应的区间。
[0046]
1、仿射型节点导纳的计算
[0047]
对于接入无功补偿装置svc的风电场并网系统，当无功补偿装置svc的补偿容量发生变化时，风电场并网系统的谐振频率随之产生变化；构造svc的补偿容量复仿射表达式如下：
[0048][0049]
其中，q
svc,0
为单个无功补偿装置svc的仿射中心值；qi由svc的额定容量决定，在复仿射表达式中为噪声元系数；εi表示svc的无功输出波动范围，取值为εi∈[-1,1]；
[0050]
基于复仿射形式的svc的补偿容量计算svc对风电场并网系统产生的节点导纳表达式如下：
[0051][0052]
式中，vb为svc的额定电压，h为谐波次数。
[0053]
2、模态阻抗的计算
[0054]
在频率f处接入svc的风电场并网系统节点导纳矩阵yf：
[0055][0056]
若系统产生频率为f的并联谐振现象，其节点电压、电流方程为：
[0057][0058]
其中，yf为在频率f处的并网系统节点导纳矩阵，vf和if分别为节点电压和节点注入电流向量；节点导纳矩阵yf分解如下：
[0059]
yf＝lλt
ꢀꢀꢀ
(5)
[0060]
式中，λ为对角特征值矩阵，λ＝diag(λ1,λ2,
…
λk,
…
)；l＝[l1,l2,
…
lk,
…
]、t＝[t1,t2,
…
tk,
…
]分别为左、右特征向量矩阵，且有l＝t-1
；
[0061]
将式(5)代入式(4)得到：
[0062]vf
＝lλ-1
tifꢀꢀꢀ
(6)
[0063]
定义uf＝tvf为模态电压向量，jf＝tif为模态电流向量，则有uf＝λ-1
jf；即：
[0064][0065]
式中，λ-1
为模态阻抗矩阵。
[0066]
在本实施例中，采用所述模态分析方法分析并网谐振不确定性的具体步骤如下：
[0067]
1)基于模态分析模型，根据式(1)计算得到svc补偿容量复仿射表达式再根据式(2)计算得到节点导纳复仿射表达式
[0068]
2)计算得到系统节点导纳矩阵y(s)；
[0069]
3)对节点导纳矩阵y(s)进行特征值分解，即y(s)＝l(s)λ(s)t(s)，从而得到左、右特征向量矩阵l(s)、t(s)及对角特征值矩阵λ(s)；
[0070]
4)计算系统频率为f时各模式下的模态阻抗；
[0071]
5)重复步骤2)-4)，直至遍历所有可能引起系统谐振的谐波频率，从而得到各谐波频率下的系统模态阻抗曲线图，进而分析风电场并网谐振现象；结合svc的仿射模型与节点导纳复仿射表达式，得到各谐波频率下的系统模态阻抗曲线，进而获取svc补偿容量与系统谐振频率的关联曲线。
[0072]
3、不确定量与谐振频率关联分析
[0073]
对风电并网系统进行模态分析，建立仿射量与并网系统谐波次数、并网系统模态阻抗的关联曲面图，如图2所示。根据图2，通过分析模态阻抗最大值所在位置，确认不同下的并网系统谐振频率，建立svc补偿容量与并网系统谐振频率的关联曲线，如图3所示。
[0074]
由图3所示，并网系统谐振频率与svc补偿容量存在正相关的关系。基于此规律，通过分析如何调节大小，实现谐振频率的调整。
[0075]
某一模式下各偶数次谐振频率所对应的区间如表1所示，由于实际电力系统中几乎不存在偶次谐波，因而将表1作为调节的依据，调节并网系统谐振频率至偶数次，以达到抑制风电场并网系统谐振的目的。
[0076]
表1与其对应的并网系统谐振频率
[0077][0078]
以上所述，仅是本发明的较佳实施例而已，并非是对本发明作其它形式的限制，任何熟悉本专业的技术人员可能利用上述揭示的技术内容加以变更或改型为等同变化的等效实施例。但是凡是未脱离本发明技术方案内容，依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与改型，仍属于本发明技术方案的保护范围。