基于DOB死区补偿下EKF的PMSLM无传感器控制方法及系统

基于dob死区补偿下ekf的pmslm无传感器控制方法及系统
技术领域
1.本发明属于电机控制领域，尤其涉及一种基于干扰观测器(dob)死区补偿下扩展卡尔曼滤波算法(ekf)的永磁同步直线电机(pmslm)无传感器控制方法。


背景技术：

2.速度和动子位置辨识精度是实现pmslm高性能控制的基础，死区时间的预留会造成逆变器输出电压误差，除了死区时间外，开关器件的开通、关断时间，开关管和二极管导通压降等非理想特性也会引起逆变器输出电压误差，进而导致采用ekf算法的pmslm无传感器控制系统对速度和动子位置辨识精度降低，因此需要对死区效应进行相应的补偿。
3.死区补偿方法大致可分为两类。一类是基于输出电压矢量脉冲宽度的死区补偿。该方法以伏秒面积相等为原则，根据电流极性产生一个与误差电压矢量大小相等而方向相反的矢量，以抵消死区效应。此类方法大部分都依赖电流极性的判断。另一类是基于脉冲时间的死区补偿法。在脉冲产生畸变之前，根据电流极性对该相加入或减去死区补偿时间，使补偿后的三相脉宽调制脉冲在相位和宽度上更接近理想脉冲，达到修正给定电压与实际输出电压之间偏差的目的。上述方法均存在计算量大的缺陷。


技术实现要素：

4.本发明的目的在于针对现有技术存在的不足，在采用ekf算法的pmslm无传感器控制系统的基础上，提出一种新型dob死区补偿方法，无需判断电流极性且计算量小，使用该方法可以实现因死区效应造成逆变器输出电压误差的补偿，提高ekf算法对速度和动子位置的辨识精度。
5.为实现上述目的，本发明采用如下技术方案：
6.一种基于dob死区补偿下ekf的pmslm无传感器控制方法，包括：
7.采用ekf估算器估计电机转速和动子位置
8.将pmslm的采样电流id、iq、电流pi调节器输出的实际电压ud、uq和转速估计值输入死区补偿dob观测器，得到死区干扰电压
9.将死区干扰电压作为前馈补偿电压，与电流pi调节器输出电压ud、uq叠加后作为死区补偿时所需控制电压指令u
d*
、u
q*
，并经过反park变换得到αβ坐标系下指令电压u
α*
、u
β*
；
10.将死区补偿时指令电压u
α*
、u
β*
，以及采样电流i
α
、i
β
输入至ekf估算器，得到死区补偿时的转速估计值和动子位置估计值
11.进一步地，所述的一种基于dob死区补偿下ekf的pmslm无传感器控制方法，还包括：
12.测量pmslm的实际三相电流，将三相电流经过clark变换得到αβ坐标系下电流i
α
和i
β
，再通过park变换得到dq坐标系下采样电流id和iq；
13.将d轴给定电流i
d*
与id的差值信号和q轴给定电流i
q*
与iq的差值信号经过电流pi
调节器调节，得到dq坐标系下实际电压ud、uq。
14.进一步地，park变换矩阵通过由动子位置换算得到的转子磁链角度建立。
15.进一步地，所述park变换矩阵为：
[0016][0017]
式(1)中：为转子磁链角度估计值，且为转子磁链角度估计值，且为由ekf算法对动子位置估计值；τ为次级极距。
[0018]
进一步地，所述死区补偿dob观测器的模型表示如下：
[0019][0020]
式中，分别为第k时刻dq坐标系下电压扰动估计值分量；ud(k-1)、uq(k-1)分别为第k-1时刻dq坐标系下初级电压分量；rs为初级电阻；id(k-1)、iq(k-1)分别为第k-1时刻dq坐标系下初级电流分量；ld、lq分别为dq坐标系下电感分量；id(k-2)、iq(k-2)分别为第k-2时刻dq坐标系下初级电流分量；ts为采样周期；ψf为次级永磁体磁链；τ为次级极距；为由ekf估计得到的第k-1时刻的初级运动速度。
[0021]
进一步地，所述死区补偿dob观测器通过以下方法构建：
[0022]
将死区效应造成的逆变器输出电压误差视为干扰电压，根据机械响应速度小于电气响应速度，且在一个微秒级采样周期内，干扰电压几乎不变，建立离散状态下干扰电压误差数学模型：
[0023][0024]
式(2)中，u
d_err
(k)、u
q_err
(k)分别表示第k时刻dq坐标系下干扰电压分量；u
d_err
(k-1)、u
q_err
(k-1)分别表示第(k-1)时刻dq坐标系下干扰电压分量；
[0025]
考虑死区效应的影响，建立dq坐标系下的pmslm数学模型：
[0026][0027]
式(3)中：ud、uq分别为dq坐标系下初级电压分量；rs为初级电阻；ld、lq分别为dq坐标系下电感分量；id、iq分别为dq坐标系下初级电流分量；ψf为次级永磁体磁链；为由ekf估计得到的初级运动速度；τ为次级极距；u
d_err
、u
q_err
分别表示dq坐标系下干扰电压分量；
[0028]
将式(3)离散化，并转化为干扰电压方程：
[0029]
[0030]
式(4)中，ud(k)、uq(k)分别为第k时刻dq坐标系下初级电压分量；id(k)、iq(k)分别为第k时刻dq坐标系下初级电流分量；id(k-1)、iq(k-1)分别为第k-1时刻dq坐标系下初级电流分量；ts为采样周期；为由ekf估计得到的第k时刻的初级运动速度；
[0031]
根据干扰电压误差数学模型和干扰电压方程，利用第(k-1)时刻的干扰电压估计第k时刻的干扰电压，得到第k时刻的干扰电压估计值电压方程：
[0032][0033]
进一步地，所述ekf估算器根据如下步骤建立：
[0034]
在αβ坐标系下，建立死区补偿时的pmslm数学模型，并将其转换为电流方程：
[0035][0036]
式(6)中：rs为初级电阻；ls为初级电感，永磁同步直线电机为表贴式pmslm，令ls＝ld＝lq，ld、lq分别为dq坐标系下电感分量；τ为次级极距；ψf为次级永磁体磁链；u
α*
、u
β*
分别为死区补偿时αβ坐标系下指令电压分量；
[0037]
根据机械响应速度小于电气响应速度，得到和的表达式：
[0038][0039]
将死区补偿时的pmslm电流方程和和的表达式转换为空间状态方程：
[0040][0041]
式中：为状态变量；u＝[u
α*uβ*
]
t
为输入变量；y＝[i
αiβ
]
t
为输出变量；f(x)为非线性矩阵，b、c为系统矩阵：
[0042][0043]
采用ekf算法将式(8)离散化，并根据离散化的数学模型搭建ekf估算器。
[0044]
进一步地，所述的一种基于dob死区补偿下ekf的pmslm无传感器控制方法，还包括：将电机的给定转速v
ref
与转速估计值的差值信号经过转速pi调节器调节后，得到q轴给定电流i
q*
。
[0045]
另一方面，一种基于dob死区补偿下ekf的pmslm无传感器控制系统，包括：
[0046]
速度和位置追踪模块，用于根据受死区效应影响下的指令电压和采样电流，采用ekf估算器估计电机转速和动子位置以及根据死区补偿时指令电压u
α*
、u
β*
，以及采样电流i
α
、i
β
，采用ekf估算器估计转速估计值和动子位置估计值
[0047]
干扰电压估算模块，用于将pmslm的采样电流id、iq、电流pi调节器输出的实际电压ud、uq和转速估计值输入死区补偿dob观测器，得到死区干扰电压
[0048]
电压控制模块，用于将死区干扰电压作为前馈补偿电压，与电流pi调节器输出电压ud、uq叠加后作为死区补偿时所需控制电压指令u
d*
、u
q*
，并经过反park变换得到αβ坐标系下指令电压u
α*
、u
β*
。
[0049]
进一步地，所述的基于dob死区补偿下ekf的pmslm无传感器控制系统，还包括：
[0050]
坐标变换模块，用于将测量的pmslm的实际三相电流经过clark变换得到αβ坐标系下电流i
α
和i
β
，再通过park变换得到dq坐标系下电流id和iq；
[0051]
电流控制模块，用于将d轴给定电流i
d*
与id的差值信号和q轴给定电流i
q*
与iq的差值信号经过电流pi调节器调节，得到dq坐标系下实际电压ud、uq。
[0052]
本发明的有益效果：
[0053]
本发明设计的新型死区补偿dob，根据机械响应速度小于电气响应速度，且在一个微秒级采样周期内，干扰电压几乎不变。因此，当前时刻的干扰电压量可由前一时刻的干扰电压估计得到。据此设计的新型dob观测器无需额外的硬件电路支持与参数离线测量，在对死区效应进行在线实时补偿时，也无需判断电流极性、计算量小且易于实现，具有较好的实用价值。
[0054]
本发明通过新型死区补偿dob观测死区干扰电压，并将其前馈补偿给速度调节器输出电压，叠加后作为所需控制电压指令，最终实现对pmslm速度和动子位置的精确辨识与控制。速度与位置检测如果采用传统的硬件传感器，不仅增加系统成本，且易受工作环境影响导致系统可靠性降低，本发明克服了上述诸多弊端的同时，实现了对死区效应导致逆变器输出电压误差的补偿，减小了速度波动，改善了电流波形质量，从而提高了对速度和动子位置辨识的精度，满足了高性能的pmslm控制要求。
附图说明
[0055]
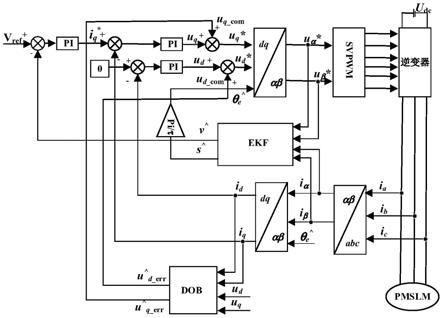
图1为本发明控制方法的系统框图；
[0056]
图2为死区扰动电压观测器框图；
[0057]
图3为理想情况下动子速度估计值、实际值与估计误差变化曲线图；
[0058]
图4为理想情况下动子位置估计值、实际值与位置估计误差变化曲线图；
[0059]
图5为死区效应影响下速度估计值、实际值与估计误差变化曲线图；
[0060]
图6为死区效应影响下动子位置估计值、实际值与位置估计误差变化曲线图；
[0061]
图7为死区补偿下动子速度估计值、实际值与估计误差变化曲线图；
[0062]
图8为死区补偿下动子位置估计值、实际值与位置估计误差图；
[0063]
图中：v
ref
为参考转速，分别为ekf算法对电机转速和动子位置估计值，为由换算得到的转子磁链角度估计值，ia、ib、ic为实际三相电流，i
α
、i
β
分别为αβ坐标系下电
流分量，id、iq分别为dq坐标系下电流分量，i
q*
为q轴给定电流，分别为dq坐标系下电压干扰估计值分量，u
d_com
、u
q_com
分别为dq坐标系下死区补偿电压分量，ud、uq分别为dq坐标系下实际电压分量，u
d*
、u
q*
分别为死区补偿时dq坐标系下指令电压分量，u
α*
、u
β*
分别为死区补偿时αβ坐标系下指令电压分量。
具体实施方式
[0064]
下面结合具体实施例对本发明作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。
[0065]
本发明提出了一种基于dob死区补偿下ekf的pmslm无传感器控制方法，采用ekf算法估计电机速度和动子位置，根据采样电流、实际电压和速度估计值计算死区干扰电压，进而将干扰电压前馈补偿给电流调节器的输出电压，叠加后作为死区补偿时所需控制电压指令，最终实现对pmslm速度和动子位置的精确控制。本发明采用的控制方法实现了对死区效应造成逆变器输出电压误差的补偿，提高了对电机速度和动子位置辨识精度，从而满足高性能的pmslm控制要求。
[0066]
在一实施例中，如图1所示，一种基于dob死区补偿下ekf的pmslm无传感器控制方法，包括以下步骤：
[0067]
步骤1，采用ekf算法估计电机转速和动子位置
[0068]
采用ekf算法的pmslm无传感器控制系统，ekf作为速度和动子位置追踪器，将追踪得到的速度和动子位置估计值作为实际速度和实际位置
[0069]
步骤2，测量pmslm的实际三相电流ia、ib、ic，将三相电流ia、ib、ic经过clark变换得到αβ坐标系下电流i
α
和i
β
，再通过park变换得到dq坐标系下电流id和iq；
[0070]
其中，park变换矩阵通过由动子位置换算得到的转子磁链角度建立。
[0071]
park变换矩阵为：
[0072][0073]
式(1)中：为转子磁链角度估计值，且为转子磁链角度估计值，且为由ekf算法对动子位置估计值；τ为次级极距。
[0074]
步骤3，将电机的给定转速v
ref
与的差值信号经过转速pi调节器调节后，得到q轴给定电流i
q*
；
[0075]
步骤4，将d轴给定电流i
d*
＝0与id的差值信号和q轴给定电流i
q*
与iq的差值信号经过电流pi调节器调节后，得到dq坐标系下实际电压ud、uq；
[0076]
步骤5，将采样电流id、iq，实际电压ud、uq和转速估计值一起输入死区补偿dob观测器，得到受死区效应影响的干扰电压估计值
[0077]
其中，死区补偿dob观测器通过以下步骤构建：
[0078]
步骤51，将死区效应造成的逆变器输出电压误差视为干扰电压，根据机械响应速度小于电气响应速度，且在一个微秒级采样周期内，干扰电压几乎不变，建立离散状态下干扰电压误差数学模型：
[0079][0080]
式(2)中，u
d_err
(k)、u
q_err
(k)分别表示第k时刻dq坐标系下干扰电压分量；u
d_err
(k-1)、u
q_err
(k-1)分别表示第(k-1)时刻dq坐标系下干扰电压分量。
[0081]
步骤52，考虑死区效应的影响，建立dq坐标系下的pmslm数学模型：
[0082][0083]
式(3)中：ud、uq分别为dq坐标系下初级电压分量；rs为初级电阻；ld、lq分别为dq坐标系下电感分量；id、iq分别为dq坐标系下初级电流分量；ψf为次级永磁体磁链；为由ekf估计得到的初级运动速度；τ为次级极距；u
d_err
、u
q_err
分别表示dq坐标系下干扰电压分量。
[0084]
步骤53，将式(3)离散化，并转化为干扰电压方程：
[0085][0086]
式(4)中，ud(k)、uq(k)分别为第k时刻dq坐标系下初级电压分量；id(k)、iq(k)分别为第k时刻dq坐标系下初级电流分量；id(k-1)、iq(k-1)分别为第k-1时刻dq坐标系下初级电流分量；ts为采样周期；为由ekf估计得到的第k时刻的初级运动速度。
[0087]
步骤54，根据干扰电压误差数学模型和干扰电压方程，利用第(k-1)时刻的干扰电压估计第k时刻的干扰电压，得到第k时刻的干扰电压估计值电压方程：
[0088][0089]
式(5)中，分别为第k时刻dq坐标系下电压扰动估计值分量；ud(k-1)、uq(k-1)分别为第k-1时刻dq坐标系下初级电压分量；id(k-2)、iq(k-2)分别为第k-2时刻dq坐标系下初级电流分量；为由ekf估计得到的第k-1时刻的初级运动速度。
[0090]
步骤6，将作为前馈补偿电压，与电流pi调节器输出电压ud、uq叠加后作为死区补偿时所需控制电压指令u
d*
、u
q*
，并经过反park变换得到αβ坐标系下指令电压u
α*
、u
β*
；
[0091]
步骤7，将死区补偿时指令电压u
α*
、u
β*
，以及采样电流i
α
、i
β
输入至ekf估算器，得到转速估计值和动子位置估计值
[0092]
其中，ekf估算器根据如下步骤建立：
[0093]
步骤71，在αβ坐标系下，建立死区补偿时的pmslm数学模型，并将其转换为电流方程；
[0094]
死区补偿时的pmslm数学模型，即死区补偿时的pmslm电压方程为：
[0095][0096]
将上式转化为电流方程：
[0097][0098]
其中：rs为初级电阻；ls为初级电感，永磁同步直线电机为表贴式pmslm，令ls＝ld＝lq；τ为次级极距；ψf为次级永磁体磁链；u
α*
、u
β*
分别为死区补偿时αβ坐标系下指令电压分量。
[0099]
步骤72，根据机械响应速度小于电气响应速度，得到和的表达式：
[0100][0101]
步骤73，将死区补偿时的pmslm电流方程和和的表达式转换为空间状态方程：
[0102][0103]
式中：为状态变量；u＝[u
α*uβ*
]
t
为输入变量；y＝[i
αiβ
]
t
为输出变量；f(x)为非线性矩阵，b、c为系统矩阵：
[0104][0105]
步骤74，采用ekf算法将式(8)离散化，据此搭建ekf估算器；
[0106]
式(8)离散化后的数学模型为：
[0107][0108]
其中，v(k)为系统噪声，w(k)为测量噪声。
[0109]
假设v(k)和w(k)均为零均值白噪声，即有
[0110]
[0111]
式中，e{}表示数学期望值。
[0112]
分别利用v、w的协方差矩阵q、r在ekf算法的递推过程中进行运算，其定义分别为：
[0113][0114]
假定v(k)和w(k)是不相关的，初始状态x(0)是随机矢量，也与v(k)和w(k)不相关。
[0115]
ekf的状态估计可由预测和校正两个阶段组成，具体步骤如下：
[0116]
利用u(k)和预测其表达式为：
[0117][0118]
式(12)中，“^”代表状态估计；“～”代表预测值；为k+1时刻状态变量预测值。
[0119]
计算对应的其表达式为：
[0120][0121]
误差协方差矩阵为：
[0122][0123]
式(14)中，f(k)为雅可比矩阵，
[0124][0125]
增益矩阵k(k+1)为：
[0126][0127]
对预测的进行反馈校正，以获得优化的状态估计即：
[0128][0129]
为了下一次的估计，要预先计算出估计误差协方差矩阵，即：
[0130][0131]
基于死区补偿时指令电压u
α*
、u
β*
，以及采样电流i
α
、i
β
估算和可以实现对pmslm速度和动子位置的辨识。
[0132]
步骤8，将u
α*
、u
β*
通过svpwm控制逆变器输出，实现对电机的转速和位置的精确辨识与控制。
[0133]
为了验证本发明控制方法的有效性，在空载条件下进行了下述对比仿真试验，参考转速v
ref
＝3mm/s，用于仿真的永磁同步直线电机参数及工况如表1所示。
[0134]
表1永磁同步直线电机参数及仿真工况
[0135][0136][0137]
由局部放大图可知，在0.25～0.3s内，如图3所示，理想情况时实际速度约为2.998mm/s，其稳态速度误差率仅为-0.067％，动子速度估计误差的波动范围为-0.053～0.035mm/s；如图4所示，动子位置估计误差的波动区间为-1.926～1.958μm。无论是对参考速度的快速追踪性还是对动子位置的高精度估计均验证了在理想情况下搭建的ekf永磁同步直线电机无传感器控制模型的正确性。
[0138]
而如图5所示，在含有死区效应影响下电机实际动子速度稳定运行在2.9365mm/s范围内，其稳态速度误差率为-2.117％，速度估计误差的波动范围变为-0.121～0.022mm/s，如图6所示，动子位置估计误差范围为-2.815～2.726μm。
[0139]
由图3～图6中数据分析对比可知，与不含死区效应的理想实际参数相比，在死区效应影响下的动子稳态速度误差率增加了2.05％，实时速度误差估计和位置误差估计波动范围增加，精度下降，表明了死区效应对ekf的pmslm无传感器控制系统性能的影响。
[0140]
由局部放大图知，在0.25～0.3s内，如图7所示，在线死区补偿下实际转速稳定运行在2.9975mm/s范围内，其稳态速度误差率为-0.083％，速度估计误差的波动范围为-0.064～0.055mm/s，如图8所示，动子位置估计误差稳定在零附近，其最小值约为-2.294μm，最大值约为2.223μm。
[0141]
由图5～图8中数据分析对比可知，与含有死区效应影响下的参数相比，在线死区补偿下的稳态速度误差率降低了2.034％，实时速度误差估计和位置误差估计波动范围减小，估计精度提高，表明本发明方法可以有效改善死区效应对ekf的pmslm无传感器控制系统带来的不利影响，证实了本控制策略的有效性。
[0142]
在另一实施例中，一种基于dob死区补偿下ekf的pmslm无传感器控制系统，包括：
[0143]
速度和位置追踪模块，用于根据受死区效应影响下的指令电压和采样电流，采用ekf估算器估计电机转速和动子位置以及根据死区补偿时指令电压u
α*
、u
β*
，以及采样电流i
α
、i
β
，采用ekf估算器估计转速估计值和动子位置估计值
[0144]
干扰电压估算模块，用于将pmslm的采样电流id、iq、电流pi调节器输出的实际电压
ud、uq和转速估计值输入死区补偿dob观测器，得到死区干扰电压
[0145]
电压控制模块，用于将死区干扰电压作为前馈补偿电压，与电流pi调节器输出电压ud、uq叠加后作为死区补偿时所需控制电压指令u
d*
、u
q*
，并经过反park变换得到αβ坐标系下指令电压u
α*
、u
β*
。
[0146]
进一步地，所述的基于dob死区补偿下ekf的pmslm无传感器控制系统，还包括：
[0147]
坐标变换模块，用于将测量的pmslm的实际三相电流经过clark变换得到αβ坐标系下电流i
α
和i
β
，再通过park变换得到dq坐标系下电流id和iq；
[0148]
电流控制模块，用于将d轴给定电流i
d*
与id的差值信号和q轴给定电流i
q*
与iq的差值信号经过电流pi调节器调节，得到dq坐标系下实际电压ud、uq。
[0149]
以上已以较佳实施例公布了本发明，然其并非用以限制本发明，凡采取等同替换或等效变换的方案所获得的技术方案，均落在本发明的保护范围内。