隔离型双有源桥直流变换器的预测控制方法及其控制装置

1.本技术属于电力电子技术领域，尤其涉及一种隔离型双有源桥直流变换器的预测控制方法及其控制装置。


背景技术：

2.近年来，隔离型双有源桥（isolated dual active bridge, dab）直流变换器拓扑因其具有功率密度高、功率可以双向流动以及易于实现软开关等优点而被广泛应用到分布式储能、直流微网、电动汽车等新兴的能源变换系统。隔离型双有源桥直流变换器的拓扑结构示意图如图1所示，在上述应用方式中隔离型双有源桥直流变换器拓扑起到了重要的接口作用，考虑到在这些应用当中，输入端的电压会产生波动且负载端也存在扰动，因此，提升隔离型双有源桥的动态响应性十分重要。
3.目前针对隔离型双有源桥控制主要采用基于线性控制器的方法对输出端电压进行跟踪控制，其中最常用的控制方法是单电压环控制，即采集输出端的电压与参考电压作差，再通过pi控制器产生移相比进行控制。然而考虑到pi控制器的参数是基于稳定运行工况点设计的，因此当系统的负载发生较大变化以及电压传输变比偏离设计值时，系统的动态响应性能会严重下降。为解决此问题，dinesh segaran等人在标题为adaptive dynamic control of a bi-directional dcdc converter（in proc. ieee 2nd energy convers. congr. expo., atlanta, ga, sep. 12
–
16, 2010, pp. 1442
–
1449.）的文献中，提出一种根据传输功率查表的方法去自适应调节控制器的参数，然而这种方法在实际执行起来比较复杂，且需要占用控制器很大的ram。随后，赵文广等人在标题为improved model-based phase-shift control for fast dynamic response of dual active bridge dc/dc converters（ieee j. emerg. sel. top. power electron., vol. 9, no. 1, pp. 223-231, feb. 2021）中提出一种基于模型的移相控制方法。这种方法虽然提高了系统的动态响应性能，但是由于控制器仍然是基于线性控制器的方法，因此在暂态过程仍存在超调和稳态误差的问题。为了进一步提升隔离型双有源桥的动态响应，研究人员提出了非线性控制策略。例如陈玲林在标题为model predictive control for dual-active-bridge converters supplying pulsed power loads in naval dc micro-grids（ieee trans. power electron., vol. 35, no. 2, pp. 1957-1966, feb. 2020）的文献中，针对接脉冲功率负载的隔离型双有源桥直流变换器提出了移动离散控制集模型预测控制方法。这种控制方法借鉴了有限控制集模型预测控制方法的思想，获得离散控制集，并通过设计自适应移相比机制对离散控制集进行更新。最后通过滚动优化的方式选择使评价函数最小的移相比作为控制输出。这种控制方法使得隔离型双有源桥直流变换器的输出电压在暂态过程几乎没有超调且稳态误差小，因此系统的动态性能得到极大的提升。
4.尽管上述控制算法能够使隔离型双有源桥直流变换器具有良好的动态性能，但是它们的性能依赖于模型的精度。而实际过程中隔离型双有源桥直流变换器的滤波电容的容值会随着使用时间的递归而有所降低，同时高频变压器的漏感感值会在变压器磁饱和时下
降。因此，在这种情况下，上述控制算法的动态性能将降低，当系统参数发生较大偏差时，动态性能甚至会恶化。


技术实现要素：

5.本技术的目的在于提供一种控制方法，用于控制隔离型双有源桥直流变换器，解决现有技术中存在的控制方法性能依赖于模型精度且鲁棒性差的问题。
6.基于以上目的，本技术提供一种隔离型双有源桥直流变换器的预测控制方法，所述方法包括以下步骤：采集第k周期的输入端电压、输出端电压和负载电流，并计算第k周期的输出端电流和输出端电压差，第k周期表示当前控制周期；构建数据驱动模型，用于表示第k周期中输出端电压差关于输出端电流和负载电流的关系，其中，所述数据驱动模型包括与第k周期的输出端电流对应的第一待定系统参数，以及，与第k周期的负载电流对应的第二待定系统参数；通过带自适应遗忘因子的递归最小二乘算法计算第k周期对应的第一待定系统参数和第二待定系统参数；采用多层递归模型，根据所述第k周期对应的第一待定系统参数和第二待定系统参数，并结合历史数据，预测第k+1周期对应的第一待定系统参数和第二待定系统参数，所述历史数据包括在第k周期前连续的r个周期所对应的r个第一待定系统参数和r个第二待定系统参数，r为自然数，表示历史数据深度；以第k周期时隔离型双有源桥直流变换器的移相比为中心确定移动离散控制集，其中，所述移动离散控制集中包括至少3个元素，各个相邻元素之间的步长为自适应步长，所述自适应步长与输出端电压参考值和第k周期输出端电压之间的电压差相关，将各个元素分别作为第k+1周期的待评估移相比；采用两步预测算法，根据所述数据驱动模型、第k周期的移相比以及第k+1周期不同的待评估移相比，预测得到分别对应不同待评估移相比的第k+2周期的输出端电压；对预测的各个第k+2周期的输出端电压进行评价，根据评价结果选择其中一个第k+2周期的输出端电压，将与该第k+2周期的输出端电压对应的第k+1周期的待评估移相比作为最优移相比，并根据所述最优移相比产生第k+1周期用于控制隔离型双有源桥直流变换器的控制信号。
7.进一步的，所述数据驱动模型表示为：；式中，；其中，δv2(k)表示的是第k周期时的输出端电压差，i
l
(k)表示的是第k周期时采样的负载电流，i2(k)表示的是第k周期时的输出端电流，a(k)表示第k周期对应的第一待定系统参数，b(k)表示第k周期对应的第二待定系统参数。
8.进一步的，所述带自适应遗忘因子的递归最小二乘算法包括如下步骤：根据所述数据驱动模型，最小二乘算法表示为：
；式中，；；根据所述最小二乘算法，带自适应遗忘因子的递归最小二乘算法的辨识过程表示为：；其中，k(k)和p(k)是k时刻的相关增益矩阵，λ是遗忘因子。
9.进一步的，所述遗忘因子的自适应算法表示为：；其中，λ0表示设定的遗忘因子边界值，τ表示一个正的时间常数， ε0表示系统设计误差范围，ε(k) 表示第k周期的辨识误差。
10.所述第k周期的系统辨识误差定义为：。
11.进一步的，其特征在于，所述多层递归模型表示如下：；式中，αi(k)和βi(k)表示在k时刻的多项式系数 (i=1，2
…
r)，r表示历史数据的深度。
12.进一步的，αi(k)和βi(k)的辨识过程表示为：；
；式中，式中，式中，式中，式中，λ
α
和λ
β
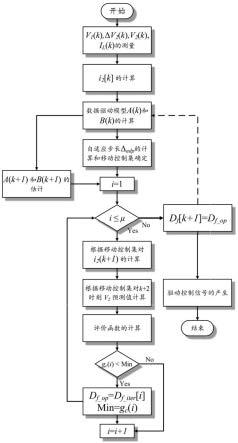
表示遗忘因子，λ
α
和λ
β
的取值接近1且不小于0.9，k
α
(k)、k
β
(k)、p
α
(k)和p
β
(k)表示在k时刻相关的增益矩阵。
13.进一步的，采用两步预测算法，预测得到第k+2周期的输出端电压表示如下：。
14.进一步的，通过评价函数对预测的第k+2周期的输出端电压进行评价，选择使评价函数计算结果为最小的一个第k+2周期时的输出端电压，将与该第k+2周期时的输出端电压对应的第k+1周期的待评估移相比作为最优移相比，所述评价函数表示如下：；式中，γ表示的权重因子，v
2ref
表示预设的输出端电压期望值，v2(k+2)表示预测的第k+2周期的输出端电压，v2(k)表示第k周期的输出端电压。
15.进一步的，所述自适应步长δ
adp
表示如下：；式中，；vs表示预设的临界电压，c表示正的调节系数，用于自适应移相比动态性能的调节，v
2ref
表示预设的输出端电压期望值。
16.本技术还提供一种隔离型双有源桥直流变换器的控制装置，包括：数据采集单元，用于采集第k周期的输入端电压、输出端电压和负载电流，并计算
第k周期的输出端电流和输出端电压差；数据处理单元，用于根据如上任一项所述的隔离型双有源桥直流变换器的预测控制方法进行数据处理，生成最优移相比；控制信号生成单元，根据所述最优移相比产生第k+1周期用于控制隔离型双有源桥直流变换器的控制信号。
17.基于以上说明，本技术提供的控制方法通过采集隔离型双有源桥直流变换器的输入和输出的变量的数据构建数据驱动模型，摆脱了传统预测控制对模型参数的依赖。并且，通过带自适应遗忘因子的递归最小二乘算法提升数据驱动模型的系统参数辨识性能，使得系统在参数或运行工况发生改变时仍能快速和准确的辨识出模型参数。同时，本技术还通过系统的实时跟踪误差确定自适应步长δ
adp
(k)的大小，并以第k周期的移相比为中心获得移动离散控制集，使得系统具有快速的动态响应能力和系统鲁棒性。同时，采用两步预测算法，预测得到第k+2周期的输出端电压以补偿数字控制延时带来的误差。
附图说明
18.图1为现有技术中隔离型双有源桥直流变换器结构示意图；图2为现有技术中三相双有源桥直流变换器的结构示意图；图3为本技术实施例提供的隔离型双有源桥直流变换器的预测控制方法流程图；图4为本技术实施例的自适应遗忘因子变化规律图；图5为本技术实施例提供的隔离型双有源桥直流变换器的控制装置示意图；图6为本技术实施例对带自适应遗忘因子的递归最小二乘算法和多层递归模型的验证结果示意图；图7为本技术实施例的控制方法的电压跟踪实验结果波形图；图8为现有技术的离散控制集模型预测控制方法的电压跟踪实验结果波形图。
具体实施方式
19.为了使阅读者能够更好的理解本方法之设计宗旨，特提供下述具体实施例，以使得阅读者能够形象的理解本方法所涉及到结构、结构组成、作用原理和技术效果。但应当注意，下述各实施例并非是对本方法技术方案的限定，本领域技术人员在对各实施例进行分析和理解的同时，可结合现有知识对本方法提供的技术方案做一系列变形与等效替换，该变形与等效替换而得的新的技术方案亦被本方法囊括在内。
20.本技术提供一种隔离型双有源桥直流变换器的预测控制方法。如图1所示，其示出了隔离型双有源桥直流变换器的结构示意图。隔离型双有源桥直流变换器包括原边电路、副边电路、变压器。通过控制器对隔离型双有源桥直流变换器的工作状态进行控制。
21.其中，原边电路的直流侧与输入端直流源v1连接，原边电路的交流侧与变压器的原边绕组电性连接。副边电路的交流侧与变压器的副边绕组电性连接，副边电路的直流侧通过输出端稳压电容与负载相连，负载端电压为v2。
22.隔离型双有源桥直流变换器的功率流向可以控制，例如，功率可以从原边电路向副边电路传递，也可以从副边电路向原边电路传递。为了便于说明，在本技术实施例中，隔离型双有源桥直流变换器的功率流向从原边电路向副边电路传递。即，原边电路的直流侧
与输入直流电源连接，其输入端电压表示为v1，副边电路的直流侧与负载相连接，其输出端电压表示为v2。在本技术实施例中，变压器的原边绕组与副边绕组匝比表示为n。
23.如图1所示，在隔离型双有源桥直流变换器的副边电路中，包括稳压电容co，设置于副边电路直流侧，用于稳定副边电路直流侧的电压。作为一种可选的实现方式，副边电路的直流侧作为隔离型双有源桥直流变换器的输出端，与负载连接。
24.因此，在隔离型双有源桥直流变换器进行功率传输时，副边电路的实际输出电流等于流经稳压电容的电流与流经负载的电流之和。为了便于说明，如图1所示，在本技术实施例中，将副边电路的实际输出电流称为输出端电流，并将输出端电流标识为i2，将流经负载的电流称为负载电流，并将负载电流标识为i
l
。
25.作为一种可选的实现方式，在对隔离型双有源桥直流变换器进行控制时，原边电路和副边电路的开关频率相同。并且，原边电路中各个开关管的导通信号与副边电路中各个开关管的导通信号之间相差一个桥间移相角，桥间移相角可以通过移相比表示，在本技术实施例中，将移相比标识为df。
26.值得说明的是，本技术实施例提供的预测控制方法不仅适用于图1所示的单相双有源桥直流变换器，同时，还适用于其它衍生类拓扑，例如三相双有源桥直流变换器、多端口双有源桥直流变换器等。如图2所示，其示出了本技术实施例提供的预测控制方法所适用的三相双有源桥直流变换器的结构示意图。
27.以上为本技术实施例提供的隔离型双有源桥直流变换器的相关说明，下面，将结合附图对本技术提供的控制方法进行详细说明。
28.为了便于说明，在本技术实施例中，第k周期表示任一周期，例如，第k周期可以表示当前控制周期，并将与当前控制周期相邻的下一周期定义为第k+1周期，将与第k+1周期相邻的下一周期定义为第k+2周期。
29.如图3所示，为本技术实施例提供的隔离型双有源桥直流变换器的预测控制方法流程图。控制方法包括如下步骤：采集第k周期的输入端电压v1、输出端电压v2和负载电流i
l
，并计算第k周期的输出端电流i2和输出端电压差δv2。
30.构建数据驱动模型，用于表示第k周期中输出端电压差δv2关于输出端电流i2和负载电流i
l
的关系，其中，所述数据驱动模型包括与第k周期的输出端电流i2对应的第一待定系统参数，以及，与第k周期的负载电流i
l
对应的第二待定系统参数。
31.通过带自适应遗忘因子的递归最小二乘算法计算第k周期对应的第一待定系统参数和第二待定系统参数。
32.采用多层递归模型，根据所述第k周期对应的第一待定系统参数和第二待定系统参数，并结合历史数据，预测第k+1周期对应的第一待定系统参数和第二待定系统参数；其中，所述第k+1周期为与所述第k周期相邻的下一控制周期，所述历史数据包括在第k周期前连续的r个周期所对应的r个第一待定系统参数和r个第二待定系统参数。r为自然数，表示历史数据的深度。
33.以第k周期时隔离型双有源桥直流变换器的移相比为中心确定移动离散控制集，其中，所述移动离散控制集中包括至少3个元素，各个相邻元素之间的步长为自适应步长，所述自适应步长与输出端电压参考值和第k周期输出端电压v2之间的电压差相关，将各个
元素分别作为第k+1周期的待评估移相比。
34.采用两步预测算法，根据所述数据驱动模型、第k周期的移相比以及第k+1周期不同的待评估移相比，预测得到分别对应不同待评估移相比的第k+2周期的输出端电压。
35.对预测的各个第k+2周期的输出端电压v2进行评价，根据评价结果选择其中一个第k+2周期的输出端电压v2，将与该第k+2周期的输出端电压v2对应的第k+1周期的待评估移相比作为最优移相比，并根据所述最优移相比产生第k+1周期用于控制隔离型双有源桥直流变换器的控制信号。
36.以上为本技术实施例提供的隔离型双有源桥直流变换器的预测控制方法，下面将结合具体情形，进一步的对该控制方法进行说明。
37.在本技术实施例中，首先采集了第k周期时隔离型双有源直流桥变换器的输入端电压v1（k）、输出端电压v2（k）和负载电流i
l
（k），并计算第k周期的输出端电流i2（k）和输出端电压差δv2（k）。
38.作为一种可选的实现方式，任一周期时的输出端电流i2可以通过公式（1）计算获得，公式（1）表示如下：
ꢀꢀ
(1)其中，i2表示任一周期对应的输出端电流，n表示变压器中原边绕组与副边绕组之间的匝比，v1表示任一周期对应的输入端电压，df表示任一周期对应的移相比，fs表示隔离型双有源直流桥变换器中开关管的开关频率，ls表示变压器的漏感之和。
39.为了摆脱传统预测控制中对模型参数的依赖，本技术实施例提供的预测控制方法构建了数据驱动模型。作为一种可选的实现方式，第k周期时的输出端电压差δv2（k）可以通过公式（2）计算获得，公式（2）表示如下：
ꢀꢀꢀꢀ
(2)式中，v2（k）表示第k周期的输出端电压，v2（k+1）表示第k+1周期的输出端电压。
40.作为一种可选的实现方式，可以认为任意相邻两个周期的输出端电压差近似，因此，输出端电压差δv2（k）还可以表示为：
ꢀꢀꢀꢀꢀ
(3)式中，v2（k）表示第k周期的输出端电压，v2（k-1）表示与第k周期相邻的上一周期的输出端电压。
41.作为一种可选的实现方式，本技术实施例提供的数据驱动模型可以通过公式（4）表示，公式（4）表示如下：
ꢀꢀꢀꢀ
(4)式中，i2（k）表示第k周期对应的输出端电流，可以通过公式（1）计算获得，i
l
(k)表示采集获得的第k周期对应的负载电流，a(k)表示第k周期的第一待定系统参数，b(k) 表示第k周期的第二待定系统参数。
42.为了实现带遗忘因子的递归最小二乘算法，可以将公式（3）改写为公式（5），公式（5）表示如下：(5)式中，；；基于公式（5），则数据驱动模型的带遗忘因子递归最小二乘辨识过程可以通过公式（6）表示，公式（6）表示如下：
ꢀꢀꢀ
(6)式中，k(k)和p(k)是k时刻的相关增益矩阵，λ是遗忘因子，它的取值通常是接近1而不小于0.9。
43.值得注意的是λ值的选择会影响递归最小二乘算法的辨识精度和收敛速度。例如当λ远小于1时，系统对待估计参数的跟踪能力将会提高，但是对噪声的鲁棒性会降低。同样地，当λ值接近1时，系统对噪声的鲁棒性能将会提升，但是对待估计参数的跟踪能力将会降低。考虑到实际过程中系统参数可能会发生变化，因此，辨识过程中λ也需要自适应变化以保证递归最小二乘算法在辨识过程中的性能。
44.作为一种可选的实现方式，本技术实施例结合公式（5）和公式（6）给出了第k周期的辨识误差的定义，辨识误差的定义可以通过公式（7）表示，公式（7）表示如下：
ꢀꢀꢀꢀꢀ
(7)根据公式（7），本技术实施例给出了自适应遗忘因子算法，自适应遗忘因子算法可以通过公式（8）表示，公式（8）表示如下：
ꢀꢀ
(8)式中，λ0是设定的遗忘因子边界值，τ是一个正的时间常数，ε0是设计的误差范围。
45.进一步的，自适应遗忘因子的变化规律如图4所示。
46.进一步的，在本技术实施例中，采用多层递归模型，根据第k周期对应的第一待定
系统参数a(k)和第二待定系统参数b(k)，并结合历史数据，预测第k+1周期对应的第一待定系统参数和第二待定系统参数。
47.作为一种可选的实现方式，将第k+1周期对应的第一待定系统参数表示为a(k+1)，将第k+1周期对应的第二待定系统参数表示为b(k+1)。
48.采用多层递归模型，根据第k周期对应的第一待定系统参数a(k)和第二待定系统参数b(k)，并结合历史数据，预测第k+1周期对应的第一待定系统参数a(k+1)和第二待定系统参数b(k+1)。
49.具体的，多层递归模型可以通过公式（9）表示，公式（9）表示如下：
ꢀꢀ
(9)式中，αi(k)和βi(k)表示在k时刻的多项式系数(i=1，2
…
r)，r表示历史数据的深度。理论上r值越大，则对a(k+1)和b(k+1)的估计就越精确，但是相应的算法结构也会变得更加复杂，从而增加系统的计算负担。在综合考虑系统的运算负担和估计的精度情况下本发明设置。
50.αi(k)和βi(k)的辨识过程可以表示为：
ꢀꢀꢀꢀꢀ
(10)
ꢀꢀ
(11)式中，式中，式中，式中，
式中，λ
α
和λ
β
表示的是上述递归最小二乘辨识过程中的遗忘因子，λ
α
和λ
β
的取值范围通常为接近1且不小于0.9，考虑到实际过程中αi(k)和βi(k)参数突变的情况很少，因此为了降低算法的复杂度在本文中的遗忘因子取定值。k
α
(k)、k
β
(k)、p
α
(k)和p
β
(k)表示在k时刻相关的增益矩阵。
51.为了提高系统的动态响应性能，本技术实施例提供一种自适应步长，用于更新移动离散控制集。作为一种可选的实现方式，在本技术实施例中，移动离散控制集中包括3个元素，各个相邻元素之间的步长为自适应步长δ
adp
。其中，自适应步长δ
adp
可以通过公式(12)表示，公式(12)表示如下：
ꢀꢀꢀꢀ
(12)式中，；vs表示预设的临界电压，c表示正的调节系数，用于自适应移相比动态性能的调节，v
2ref
表示预设的输出端电压期望值。
52.因此，以第k周期时隔离型双有源桥直流变换器的移相比df(k)为中心确定的移动离散控制集包括元素如下：d
f_iter
[i]∈[df(k)-δ
adp
，df(k)，df(k)+δ
adp
]。
[0053]df_iter
[i]表示第i次计算时对应的移动离散控制集中元素的取值。
[0054]
将以上列出的移动离散控制集中各个元素分别作为第k+1周期的待评估移相比。
[0055]
如图3所示，根据本技术提供的控制方法，在确定了自适应步长δ
adp
以及移动离散控制集后，需要通过滚动优化的方法，求得不同移相比下的控制电流i2(k+1)，并计算出对应预测获得的第k+2周期的输出端电压v2(k+2)。
[0056]
具体的，本技术实施例需要进行i（i= 1，2，
…
, μ）次滚动优化，其中，μ等于移动离散控制集中元素的数量，例如，在本技术实施例中，μ=3。
[0057]
为了补偿数字控制延时带来的误差，作为一种可选的实现方式，采用两步预测算法，分别代入移动离散控制集中的各个元素可以预测得到多个第k+2周期的输出端电压v2(k+2)。
[0058]
作为一种可选的实现方式，结合公式（4）提供的数据驱动模型，可以得到第k+2周期时的输出端电压表达式，第k+2周期时的输出端电压表达式可以通过公式（13）表示，公式（13）表示如下：(13)对于公式（13），第k+2周期时的输出端电压v2(k+2)的计算结果可以结合公式（1）、公式（5）以及公式（9）获得。其中，在利用公式（1）预测第k+1周期对应的输出端电流i2(k+1)时，根据待评估移相比的选择不同，其计算的输出端电流i2(k+1)也有所不同，因此，最终可以获得多个第k+2周期的输出端电压v2(k+2)。
[0059]
作为一种可选的实现方式，本技术实施例提供评价函数，用于对预测的各个第k+2
周期的输出端电压v2进行评价。评价函数通过公式（14）表示，公式（14）表示如下：
ꢀꢀꢀꢀꢀ
（14）式中，γ表示的是权重因子。
[0060]
依次将各个第k+2周期时的输出端电压v2(k+2)代入评价函数中，选择使评价函数计算结果为最小的一个第k+2周期时的输出端电压v2(k+2)，将与该第k+2周期时的输出端电压v2(k+2)对应的第k+1周期的待评估移相比作为最优移相比，根据所述最优移相比产生第k+1周期用于控制隔离型双有源桥直流变换器的控制信号。
[0061]
具体的，如图3所示，根据本技术实施例提供的控制方法，min=gc(i)表示取i个评价函数中的最小值，i表示滚动优化次数，d
f_iter
[i]表示第i次计算时对应的移动离散控制集中元素的取值，d
f_op
表示最优移相比。根据以上说明可知，本技术提供的控制方法选择使评价函数最小的移相比作为最优移相比，并将该最优移相比用于第k+1周期。
[0062]
如图5所示，本技术还提供一种隔离型双有源桥直流变换器的控制装置，包括：数据采集单元，用于采集第k周期的输入端电压、输出端电压和负载电流，并计算第k周期的输出端电流和输出端电压差；数据处理单元，用于根据如上任一项所述的隔离型双有源桥直流变换器的预测控制方法进行数据处理，生成最优移相比；控制信号生成单元，根据所述最优移相比产生第k+1周期用于控制隔离型双有源桥直流变换器的控制信号。
[0063]
如图6所示，其示出了本技术实施例对带自适应遗忘因子的递归最小二乘算法和多层递归模型的验证结果示意图。实验结果给出了数据驱动模型中，第k周期对应的第一待定系统参数a(k)和第二待定系统参数b(k)，及预测第k+1周期对应的第一待定系统参数a(k+1)和第二待定系统参数b(k+1)的估计值。从结果可以发现本发明提出的算法在0.2s内就能实现算法的收敛，且多层递归模型对a(k+1)和b(k+1)的估计误差小于1%符合工程要求。
[0064]
为了验证本发明的控制算法的鲁棒性，我们与传统的移动离散控制集模型预测控制进行电压跟踪对比实验。实验中控制器中采用的输出电容参数和变压器漏感参数偏离实际值的20%。
[0065]
结合图7和图8，其示出了电压跟踪实验结果。从实验结果可以发现本发明在参数不匹配情况下仍然具体良好的动态响应能力且稳态误差很小。因此本发明提出的针对隔离双有源桥直流变换器拓扑的无模型移动离散控制集预测控制算法具有优异的动态响应和参数鲁棒能力。
[0066]
上述对实施例的描述是为便于本技术领域的普通技术人员能理解和应用本发明。熟悉本领域技术的人员显然可以容易地对上述实施例做出各种修改，并把在此说明的一般原理应用到其他实施例中而不必经过创造性的劳动。因此，本发明不限于上述实施例，本领域技术人员根据本发明的揭示，对于本发明做出的改进和修改都应该在本发明的保护范围之内。