一种含SVG风电场的振荡控制方法与流程

一种含svg风电场的振荡控制方法
技术领域
1.本发明属于新能源发电建模领域，具体来说，涉及一种含svg的风电场全尺度电磁暂态建模及对其振荡影响因素分析的方法。


背景技术：

2.随着地球资源的日渐衰竭以及人们对环境问题的关注，可再生能源的接入越来越受到世界各国的重视。风是没有公害的能源之一，而且它取之不尽，用之不竭。对于缺水、缺燃料和交通不便的沿海岛屿、草原牧区、山区和高原地带，因地制宜地利用风力发电，非常适合。
3.风力发电的原理，是利用风力带动风车叶片旋转，再透过增速机将旋转的速度提升，来促使发电机发电。依据风车技术，大约是每秒三米的微风速度(微风的程度)，便可以开始发电。风力发电正在世界上形成一股热潮，因为风力发电不需要使用燃料，也不会产生辐射或空气污染。
4.然而，当前环境下的风力发电仍然存在着诸多问题和挑战急需解决，由于依赖于风速这种不稳定能源，风力发电的功率具有波动性和间歇性的特点，而大量基于电力电子设备的非同步电源和的接入形成了新型电力系统，使得大型风力发电场和临近电力电子设备以及电网之间的交互作用会变得十分复杂。而当系统中出现扰动时，风电场极有可能产生振荡，并对电网稳定性产生挑战。因此，风电机组必须接入svg系统实现动态无功补偿功能，以保证故障出现时能维持其运行的稳定性。此外，还需对风电机组振荡原因进行具体分析，以保证其稳定性。


技术实现要素：

5.本部分的目的在于概述本发明的实施例的一些方面以及简要介绍一些较佳实施例。在本部分以及本技术的说明书摘要和发明名称中可能会做些简化或省略以避免使本部分、说明书摘要和发明名称的目的模糊，而这种简化或省略不能用于限制本发明的范围。
6.鉴于上述现有存在的问题，提出了本发明。
7.因此，本发明解决的技术问题是：实现svg接入风电机组并分析其受扰动下如何提高稳定性避免振荡，该模型能够实现风电机组面对故障时能依靠svg实现动态无功补偿保持稳定性，且能根据对振荡的影响因素分析有效提高风电机组的稳定运行能力，使在产生扰动时保持稳定运行，尽可能降低振荡对风电机组的影响。
8.为解决上述技术问题，本发明提供如下技术方案：一种含svg的风电场建模及对其振荡影响因素分析的方法，包括：
9.基于风电场实际情况搭建全尺度电磁暂态模型；
10.在已搭建好的风电机组模型中接入svg并验证接入svg的作用；
11.针对风机和svg内部各控制参数对振荡的影响进行分析，通过控制风电机组的参数变量，从而抑制振荡。
12.作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：搭建风电场全尺度电磁暂态模型，包括：
13.本发明基于实际情况搭建风力发电机组模型。本全尺度风电机组模型的建模思路是构建风力机模型，后构建齿轮箱组件连接感应发电机，再接入系统中。风电机组模型是根据特定的风能利用系数、风速和发电机转速来模拟实际运行中的风电机组的工作状况。风力机内部由模拟风速输出的风源元件和相关调速器组成。
14.作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：本风力机仿真模型的特点在于，包括：
15.输入风机的风速信号vw由风源元件产生，风源风速采用了内部输入与外部输入并行的方式，可在运行过程中自行调整外部的风速输入，也可分别自行设定风轮扫动面积、空气密度等影响风机输出的参数，来实现可完全模拟任何实际的运行状况以达到全尺度仿真的目的。其中该模型设置的风力机传递至发电机的风功率表示为：
[0016][0017]
其中p
out
为风力机的功率输出，单位：瓦；ρ为空气密度，单位：千克/立方米；a为风轮扫掠面积，单位：立方米；vw为风速，单位：米/秒；η
gr
为齿轮箱效率系数；c
p
为风能利用系数，他是桨距角β与叶尖速比λ的函数。
[0018]
该全尺度风机模型实现并网的基本的工作原理是：在发电机的转速建立以前，通过反并联晶匣管并网，此时系统中为其提供有功功率和无功功率，而风力机则提供转矩，带动着发电机增速。晶匣管的触发角随着发电机速度的增大而逐渐减小，因此，通过所述方法即可实现发电机速度平稳上升，进而可以避免产生冲击电流干扰稳定性。
[0019]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：所述仿真模型还包括：
[0020]
将搭建好的风机模型与系统侧用于模拟无穷大母线的三相交流电源相连接。此模型的重点在于双pwm变换器及其控制。网侧变换器的数学模型可表示为：
[0021][0022][0023][0024]
根据上三式，可以得到
[0025]
ed＝-lx1+vd+ωliq[0026]eq
＝-lx2+ωlid[0027]
其中，r和l为变换器的连接阻抗和电感；id，iq分别为d轴，q轴的实际电流；vd为系统电压的d轴分量；ed和eq分别为变换器输出电压的d轴和q轴分量。
[0028]
忽略连接电阻r时，若按照以上公式进行变换器输出参考电压的计算，将可实现dq
解耦控制。基于电力系统计算机辅助设计/含直流电磁暂态仿真(英文简称：pscad/emtdc)平台搭建仿真风机机组并网模型，调试运行直至不产生报错。
[0029]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：在已搭建好的风电机组模型中接入svg，包括：
[0030]
根据以上步骤搭建好的风电机组模型，将svg部件接入该风机系统中，并验证其是否发挥作用。其中，svg系统是建立在一个静止的同步电压源的基础上，其具体的工作原理是将自换相桥式电路经过一个串联电抗(其中包括有变压器的漏抗及其他电抗)与电网相连，根据输入的系统的无功功率和有功功率的指令，适当地调节桥式电路交流侧输出电压的幅值和相位，或者直接控制其交流侧电流就可以使该系统吸收或发出满足系统所需的无功电流，实现动态无功补偿的目的。在接入svg后，调试程序至不产生报错，并观察电压功率输出波形是否稳定。
[0031]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：验证接入svg的作用，包括：
[0032]
在实现svg接入风电机组并调试运行成功后，在风电机组并网点处设置一个短时的故障工况，分别记录未接入svg和接入svg后系统的电压及功率变化情况，在此基础上分析svg是否实现其作用。在接入svg之后，在风机并网处设置一个短时间三相短路故障，分别观察接入和接入svg前风机侧受故障影响下的仿真波形，并进行比较。若svg正确接入，在并网处产生故障时，svg将输出无功，维持风机侧电压和有功在极短时间内恢复稳定运行时的状态。根据仿真结果，进行适当参数调整，保证svg能正常发挥作用。
[0033]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：分析风机侧参数对于振荡可能产生的影响，包括：
[0034]
分析风机对系统扰动的响应与风机侧参数的关系。在系统产生扰动的情况下，由于双馈风力发电机组的定子侧直接会与系统侧相连，所以扰动量会存在与风电机组的定子中，因此机组内部的控制系统所采集到的瞬时电气参数均会发生相应的变化，进而导致转子侧输出的电压，电流产生变化。与其同时，由于定子侧与转子侧之间存在耦合相互作用，使得定子侧也会出现对应的电压电流的变化，然后与系统侧产生的原始扰动产生叠加，使情况更加复杂，若此时风电机组产生了明显振荡，则可能存在无法恢复稳态，严重时甚至产生电压崩溃的情况。而双馈风电机组转子侧变流器内部的电流内环控制参数则是该风机系统面对扰动时影响振荡的关键，该电流表示为：
[0035][0036]
其中，i
re
代指双馈机组反馈到系统侧的受扰动后的电流，a为常数，td为积分时间常数，kd为内环增益。
[0037]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：还包括：
[0038]
根据参数与振荡的具体关系完成仿真的设计。可以看出由于转子侧内环控制的积分时间常数td与内环增益kd存在数学关系使得这两个参数可以控制双馈风电机组受扰动后反作用于系统的相互激励的情况。由此采用控制变量的思想，在原本受到扰动会产生振荡的仿真场景下：
[0039]
[1]保持参数kd的数值不变，适当增大td的值，由于正相关的数学关系存在，此时反
作用于系统的相互激励就越弱，即系统应该可以更快恢复稳定性。
[0040]
[2]验证在保持参数td不变的情况下，适当减小参数kd的值，观察对应情况。
[0041]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：分析接入的svg侧相关控制参数对于系统产生扰动时风机组产生振荡可能的影响，包括：
[0042]
分析svg对系统扰动的响应与svg参数间的关系。由于静止无功发生器的内环控制策略与双馈风力发电机组相似，在svg内部也存在控制参数p
gain
和时间常数t
const
共同控制反作用于系统的激励，故采取一样的分析方法来研究。在系统扰动下，svg内部内部的控制系统采集的瞬时电压会发生变化，导致交流电压控制环路输出的触发脉冲信号产生了变化，并使svg感应出扰动电流，该扰动电流将与原始扰动叠加，对振荡起到附加作用，该扰动电流表示为：
[0043][0044]
其中，i
ref
代指svg反馈到系统侧的受扰动后的电流，g为控制回路的参数，此处可视为常数，t
const
为积分时间常数。
[0045]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：还包括：
[0046]
根据参数与振荡的具体关系完成仿真的设计。可以看出由于控制回路的积分时间常数t
const
与内环增益p
gain
存在某种数学关系使得这两个参数可以控制svg受扰动后反作用于系统的相互激励的情况。由此采用控制变量的思想，在原本受到扰动会产生振荡的仿真场景下：
[0047]
[1]保持参数p
gain
的数值不变，适当增大t
const
的值，由于正相关的数学关系存在，此时反作用于系统的相互激励就越弱，即系统应该可以更快恢复稳定性。
[0048]
[2]验证在保持参数t
const
不变的情况下，适当减小参数p
gain
的值，观察对应情况。
[0049]
本发明的有益效果：该风电机组全尺度电磁暂态仿真模型的建立，有助于更加准确的模拟实际风电场的运行特性，分析影响振荡的关键因素，有利于提高风电场的振荡抑制能力，支撑风电场安全稳定运行。
附图说明
[0050]
为了更清楚地说明本发明实施例的技术方案，下面将对实施例描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其它的附图。其中：
[0051]
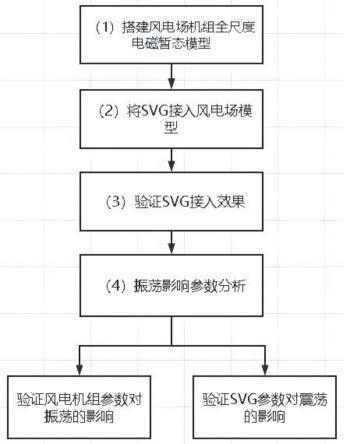
图1是本发明实施例提供的一种含svg风电场的振荡控制方法的整体流程图；
[0052]
图2是本发明实施例提供的一种含svg风电场的振荡控制方法的结构原理图；
[0053]
图3是本发明实施例一提供的一种含svg风电场的振荡控制方法的接入svg前系统遇到故障时电压变化情况；
[0054]
图4是本发明实施例一提供的一种含svg风电场的振荡控制方法的接入svg后电压变化情况；
[0055]
图5是本发明实施例一提供的一种含svg风电场的振荡控制方法的svg无功释放情况；
[0056]
图6是本发明实施例二提供的一种含svg风电场的振荡控制方法的初始场景下的系统振荡仿真结果图；
[0057]
图7是本发明实施例二提供的一种含svg风电场的振荡控制方法的控制一个参数下的系统振荡仿真结果图；
[0058]
图8是本发明实施例二提供的一种含svg风电场的振荡控制方法的控制另一参数下的系统振荡仿真结果图。
具体实施方式
[0059]
为使本发明的上述目的、特征和优点能够更加明显易懂，下面结合说明书附图对本发明的具体实施方式做详细的说明，显然所描述的实施例是本发明的一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明的保护的范围。
[0060]
在下面的描述中阐述了很多具体细节以便于充分理解本发明，但是本发明还可以采用其他不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似推广，因此本发明不受下面公开的具体实施例的限制。
[0061]
其次，此处所称的“一个实施例”或“实施例”是指可包含于本发明至少一个实现方式中的特定特征、结构或特性。在本说明书中不同地方出现的“在一个实施例中”并非均指同一个实施例，也不是单独的或选择性的与其他实施例互相排斥的实施例。
[0062]
本发明结合示意图进行详细描述，在详述本发明实施例时，为便于说明，表示器件结构的剖面图会不依一般比例作局部放大，而且所述示意图只是示例，其在此不应限制本发明保护的范围。此外，在实际制作中应包含长度、宽度及深度的三维空间尺寸。
[0063]
同时在本发明的描述中，需要说明的是，术语中的“上、下、内和外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。此外，术语“第一、第二或第三”仅用于描述目的，而不能理解为指示或暗示相对重要性。
[0064]
本发明中除非另有明确的规定和限定，术语“安装、相连、连接”应做广义理解，例如：可以是固定连接、可拆卸连接或一体式连接；同样可以是机械连接、电连接或直接连接，也可以通过中间媒介间接相连，也可以是两个元件内部的连通。对于本领域的普通技术人员而言，可以具体情况理解上述术语在本发明中的具体含义。
[0065]
实施例1
[0066]
参照图1—2，为本发明的一个实施例，提供了一种基含svg风电场的振荡控制方法，包括：
[0067]
s1：搭建风电场全尺度电磁暂态模型
[0068]
基于实际情况搭建风力发电机组模型。本全尺度风电机组模型的建模思路是构建风力机模型，后构建齿轮箱组件连接感应发电机，再接入系统中。风电机组模型是根据特定的风能利用系数、风速和发电机转速来模拟实际运行中的风电机组的工作状况。风力机内部由模拟风速输出的风源元件和相关调速器组成。本风力机仿真模型的特点在于，输入风机的风速信号vw由风源元件产生，风源风速采用了内部输入与外部输入并行的方式，可在
运行过程中自行调整外部的风速输入，也可分别自行设定风轮扫动面积、空气密度等影响风机输出的参数，来实现可完全模拟任何实际的运行状况以达到全尺度仿真的目的。其中该模型设置的风力机传递至发电机的风功率为
[0069][0070]
在式(1)中，p
out
为风力机的功率输出，单位：瓦；ρ为空气密度，单位：千克/立方米；a为风轮扫掠面积，单位：立方米；vw为风速，单位：米/秒；η
gr
为齿轮箱效率系数；c
p
为风能利用系数，他是桨距角β与叶尖速比λ的函数。
[0071]
该全尺度风机模型实现并网的基本的工作原理是：在发电机的转速建立以前，通过反并联晶匣管并网，此时系统中为其提供有功功率和无功功率，而风力机则提供转矩，带动着发电机增速。晶匣管的触发角随着发电机速度的增大而逐渐减小，因此，通过所述方法即可实现发电机速度平稳上升，进而可以避免产生冲击电流干扰稳定性。
[0072]
将搭建好的风机模型与系统侧用于模拟无穷大母线的三相交流电源相连接，线电压额定值设定为220kv；线路参数为2.5ω电阻串联0.04h电抗。升压变为y/y联结，电压比为20kv/0.69kv。其中绕线电动机设置为额定线电压0.69kv，额定功率2.5mva，定转子绕线比为0.3。此模型的重点在于双pwm变换器及其控制。
[0073]
网侧变换器的数学模型可表示为：
[0074][0075][0076][0077]
根据上三式，可以得到
[0078]
ed＝-lx1+vd+ωliqꢀꢀ
(5)
[0079]eq
＝-lx2+ωlidꢀꢀ
(6)
[0080]
上述式中，r和l为变换器的连接阻抗和电感；id，iq分别为d轴，q轴的实际电流；vd为系统电压的d轴分量；ed和eq分别为变换器输出电压的d轴和q轴分量。
[0081]
忽略连接电阻r时，若按照式(2)-(6)进行变换器输出参考电压的计算，将可实现dq解耦控制。基于电力系统计算机辅助设计/含直流电磁暂态仿真(英文简称：pscad/emtdc)平台搭建仿真风机机组并网模型，调试运行直至不产生报错。
[0082]
s2：在已搭建好的风电机组模型中接入svg并验证接入svg的作用。
[0083]
根据搭建好的风电机组模型，将svg部件接入该风机系统中，并验证其是否发挥作用。其中，svg系统是建立在一个静止的同步电压源的基础上，其具体的工作原理是将自换相桥式电路经过一个串联电抗(其中包括有变压器的漏抗及其他电抗)与电网相连，根据输入的系统的无功功率和有功功率的指令，适当地调节桥式电路交流侧输出电压的幅值和相位，或者直接控制其交流侧电流就可以使该系统吸收或发出满足系统所需的无功电流，实现动态无功补偿的目的。在接入svg后，调试程序至不产生报错，并观察电压功率输出波形是否稳定。接入svg后的仿真风机组出口电压690v，经过升压变接入220kv母线，风电机组出
力200mw左右；svg容量为300mvar，电压为25kv；系统短路容量为476.3mva，短路比约为2.13。
[0084]
在实现svg接入风电机组并调试运行成功后，在风电机组并网点处设置一个短时的故障工况，分别记录未接入svg和接入svg后系统的电压及功率变化情况，在此基础上分析svg是否实现其作用。在接入svg之后，在风机并网处设置一个短时间三相短路故障，分别观察接入和接入svg前风机侧受故障影响下的仿真波形，并进行比较。若svg正确接入，在并网处产生故障时，svg将输出无功，维持风机侧电压和有功在极短时间内恢复稳定运行时的状态。根据仿真结果，进行适当参数调整，保证svg能正常发挥作用。结果如图3，图4所示，图3为接入svg前系统遇到故障时电压变化情况，图4为接入svg后电压变化情况；svg无功释放情况如图5所示，可以清楚看到，接入svg之后的风电机组面对故障时能够更快地恢复到原有的运行状态。
[0085]
s3：针对风机和svg内部各控制参数对振荡的影响进行分析，通过控制风电机组的参数变量，从而抑制振荡。
[0086]
首先分析风机侧参数对于振荡可能产生的影响。
[0087]
应说明的是，分析风机对系统扰动的响应与风机侧参数的关系。在系统产生扰动的情况下，由于双馈风力发电机组的定子侧直接会与系统侧相连，所以扰动量会存在与风电机组的定子中，因此机组内部的控制系统所采集到的瞬时电气参数均会发生相应的变化，进而导致转子侧输出的电压，电流产生变化。与其同时，由于定子侧与转子侧之间存在耦合相互作用，使得定子侧也会出现对应的电压电流的变化，然后与系统侧产生的原始扰动产生叠加，使情况更加复杂，若此时风电机组产生了明显振荡，则可能存在无法恢复稳态，严重时甚至产生电压崩溃的情况。而双馈风电机组转子侧变流器内部的电流内环控制参数则是该风机系统面对扰动时影响振荡的关键。
[0088][0089]
在式(7)中，i
re
代指双馈机组反馈到系统侧的受扰动后的电流，a为常数。
[0090]
根据参数与振荡的具体关系完成仿真的设计。可以看出由于转子侧内环控制的积分时间常数td与内环增益kd存在某种数学关系使得这两个参数可以控制双馈风电机组受扰动后反作用于系统的相互激励的情况。由此采用控制变量的思想，在原本受到扰动会产生振荡的仿真场景下：
[0091]
[1]保持参数kd的数值不变，适当增大td的值，由于正相关的数学关系存在，此时反作用于系统的相互激励就越弱，即系统应该可以更快恢复稳定性。
[0092]
[2]验证在保持参数td不变的情况下，适当减小参数kd的值，观察对应情况。
[0093]
接着是分析接入的svg侧相关控制参数对于系统产生扰动时风机组产生振荡可能的影响。
[0094]
应说明的是，分析svg对系统扰动的响应与svg参数间的关系。由于静止无功发生器的内环控制策略与双馈风力发电机组相似，在svg内部也存在控制参数p
gain
和时间常数t
const
共同控制反作用于系统的激励，故采取一样的分析方法来研究。在系统扰动下，svg内部内部的控制系统采集的瞬时电压会发生变化，导致交流电压控制环路输出的触发脉冲信号产生了变化，并使svg感应出扰动电流，该扰动电流将与原始扰动叠加，对振荡起到附加
作用。
[0095][0096]
在式(8)中，i
ref
代指svg反馈到系统侧的受扰动后的电流，g为控制回路的参数，此处可视为常数，t
const
为积分时间常数。
[0097]
作为本发明所述的含svg风电场的振荡控制方法的一种优选方案，其中：还包括：
[0098]
根据参数与振荡的具体关系完成仿真的设计。可以看出由于控制回路的积分时间常数t
const
与内环增益p
gain
存在某种数学关系使得这两个参数可以控制svg受扰动后反作用于系统的相互激励的情况。由此采用控制变量的思想，在原本受到扰动会产生振荡的仿真场景下：
[0099]
[1]保持参数p
gain
的数值不变，适当增大t
const
的值，由于正相关的数学关系存在，此时反作用于系统的相互激励就越弱，即系统应该可以更快恢复稳定性。
[0100]
[2]验证在保持参数t
const
不变的情况下，适当减小参数p
gain
的值，观察对应情况。
[0101]
实施例2
[0102]
仿真的svg风电系统设计如图4所示。首先，根据实际情况分析，适当地降低了系统的短路电流，从而减小风电场的短路比，将短路比降低到了1.5左右，此时的系统相比原来更加不稳定，更容易观察出振荡。设置在某一时刻断开连接在风电机组并网侧的负荷，观察并网点处的电压振荡情况，并基于该系统分别考虑分别考虑双馈风电机组转子侧变流器控制参数和statcom控制参数对并网系统稳定性的影响。振荡情况如图6所示，从图中可以很清晰的观察到，在此场景下风机系统振荡持续了很长时间。记录此时的参数,：kd＝0.1；td＝＝0.2；p
gain
＝10；t
const
＝1；
[0103]
将kd的值调整为0.005，保持其他参数不变，结果如图7所示，可以观察到系统振荡有了明显改善，并且在很短的时间内恢复稳定。
[0104]
调整td的值为0.5，保持其他参数不变，结果如图7所示，可以观察到系统振荡有了明显改善，并且在很短的时间内恢复稳定。
[0105]
调整t
const
的值为2，保持其他参数不变，结果如图8所示，可以观察到系统振荡有了明显改善，并且在很短的时间内恢复稳定。
[0106]
调整p
gain
的值为2，保持其他参数不变，结果如图8所示，可以观察到系统振荡有了明显改善，并且在很短的时间内恢复稳定，且此场景下系统振荡幅度最小。
[0107]
经实际验证，双馈风电机组的控制参数和svg的控制参数均会对系统在经受扰动时振荡的情况产生影响，而具体的仿真结果也验证了之前分析的合理性。
[0108]
本发明所设计出的含svg的风电场建模及在此模型基础上的振荡影响因素的分析，使得风电场遭遇故障以及连接大电网后遭遇系统扰动时，均能实现尽快恢复到稳定运行的状态，有助于对于新能源系统并网稳定性的认识，并提供了一种可行的分析方法。