一种基于模型预测控制的直驱式波浪发电系统弱磁控制策略

1.本发明属于可再生能源发电的技术领域，特别涉及了波浪能发电技术，具体而言涉及一种基于模型预测控制的直驱式波浪发电系统弱磁控制策略。


背景技术：

2.科学的开发和利用波浪能对缓解能源危机和环境污染问题，具有重要的意义。在众多类型的波浪发电装置中，直驱式波浪发电系统具有系统结构简单、效率高的优点，已经成为波浪能开发利用的研究热点。为了提高直驱式波浪发电系统的发电效率，必须采取有效的控制策略，以在满足发电系统状态量实际约束的前提下，实现波浪能最大功率捕获。传统波浪发电系统控制策略包括实部控制和复共轭控制，其中，实部控制捕获的功率较小，复共轭控制捕获的功率很大，但系统状态量易超出实际允许范围，影响系统的正常工作。另一方面，对于波浪发电系统中永磁直线发电机定子电流矢量控制，为降低损耗，常采用id＝0的控制方式。而实际海况变化复杂，且时有大幅波动，易导致浮子速度超出允许值，此时若不采取额外控制，将超过发电机额定容量，且发电机反电动势的升高会导致直流母线电压过调制，引起定子电流波形的畸变。


技术实现要素：

3.针对现有技术存在的缺陷与不足，本发明目的在于提供一种基于模型预测控制的直驱式波浪发电系统弱磁控制策略，使得直驱式波浪发电系统能够在满足物理约束的情况下，提取的功率达到最大；另外，利用弱磁控制的定子电流矢量控制方式，有效地拓宽了永磁直线电机的运行速域。
4.根据本发明为实现上述发明目的采用如下技术方案：
5.一种基于模型预测控制的直驱式波浪发电系统弱磁控制策略，包括以下步骤：
6.s1：根据直驱式波浪发电系统中浮子的受力情况和牛顿第二定律，建立直驱式波浪发电系统的机械运动模型；
7.s2：建立直驱式波浪发电系统的直线永磁电机模型；
8.s3：根据直驱式波浪发电系统的机械运动模型和直线永磁电机模型，建立基于模型预测控制的直驱式波浪发电系统的状态空间模型；
9.s4：基于直驱式波浪发电系统的控制目标，建立功率优化目标函数，再根据功率优化目标函数对状态空间模型进行增广并转换到离散域，得到直驱式波浪发电系统的离散状态空间模型；
10.s5：对离散状态空间模型进行状态量的滚动优化，直至完成滚动预测控制，实现系统的在线优化求解；
11.s6：设置系统的约束条件，在直线永磁电机的动子速度处于正常范围内时，采用id＝0的控制方法，在动子速度超过正常范围时，采用弱磁控制方法。
12.本发明的进一步方案是，s1建立的直驱式波浪发电系统的机械运动模型表达式
为：
[0013][0014]
式中，m为浮子质量，m
add
为水的附加质量，两者共同组成了浮子的等效总质量；z(t)为浮子的升沉位移，为浮子的运动速度，为浮子的运动加速度；阻尼系数k(t)与速度的卷积项对应浮子受到的辐射力fr(t)；浮子位移z(t)与弹性系数ks的乘积对应浮子受到的等效弹簧阻力fs(t)；f
wave
为作为输入的波浪激励力；f
pto
为来自系统动力输出装置(power take-off，pto)的外加电磁推力。
[0015]
本发明的更进一步方案是，采用状态空间模型近似替代机械运动模型表达式中的辐射力fr(t)。
[0016]
本发明的进一步方案是，s3建立的状态空间模型表达式为：
[0017][0018]
式中，v(t)为缩放后的波浪激励力；uq(t)为系统的控制量。
[0019]
本发明的进一步方案是，s4建立的功率优化目标函数包含pto力f
pto
惩罚项，该功率优化目标函数的表达式为：
[0020][0021]
式中，为浮子的速度变化量，r表示惩罚系数。
[0022]
本发明的进一步方案是，s6的约束条件包括线性约束和非线性约束，其中线性约束包括浮子的升沉位移z(t)、运动速度和pto力f
pto
，表达式如下：
[0023][0024]
非线性约束包括直线永磁电机的定子电压、定子电流和弱磁率τ，表达式如下：
[0025][0026]
式中，ud为d-q旋转坐标系下d轴电压，uq为q轴电压；id为d轴电流，iq为q轴电流，is为定子绕组的电流；ls为定子绕组的电感；ψ
pm
为永磁体转子在定子中产生的磁链。
[0027]
本发明与现有技术相比，具有以下有益效果：
[0028]
在满足系统约束的情况下，提高直驱式波浪发电系统的功率捕获性能，并有效拓宽永磁直线发电机的运行速域，提高系统运行的稳定性。
附图说明
[0029]
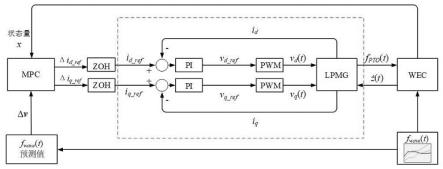
图1为基于模型预测控制的直驱式波浪发电系统内外环控制框图；
[0030]
图2为直驱式波浪发电系统受力图；
[0031]
图3为永磁直线电机定子电流矢量运行范围示意图。
具体实施方式
[0032]
下面配合所附图式对发明的技术方案进行详细说明：
[0033]
基于模型预测控制的直驱式波浪发电系统内外环控制框图如图1所示，在外环模型预测控制结构中，为获得较高的调节速度和控制精度，将直线电机的定子q轴电流参考值增量δi
q_ref
、d轴电流参考值增量δi
d_ref
作为控制算法的控制量输出，未来波浪力预测值δv作为不可控输入，浮子的位移z(t)、速度等参数作为状态量。经滚动优化输出的最优控制量通过零阶保持后得到q轴电流参考值i
q_ref
、d轴电流参考值i
d_ref
，再经电流内环解耦后采用pi控制器跟踪参考信号，最后采用pwm技术调制信号，完成系统的优化控制过程。
[0034]
本发明涉及的具体步骤描述见下：
[0035]
步骤1、建立直驱式波浪发电系统的机械运动模型：
[0036]
对于直驱式波浪发电系统的机械运动方程，根据直驱式波浪发电系统中浮子的受力情况(如图2所示)和牛顿第二定律，建立直驱式波浪发电系统的简化运动方程，表达式如下：
[0037][0038]
式中，m为浮子质量，m
add
为水的附加质量，两者共同组成了浮子的等效总质量；z(t)为浮子的升沉位移，为浮子的运动速度，为浮子的运动加速度；阻尼系数k(t)与速度的卷积项对应浮子受到的辐射力fr(t)；浮子位移z(t)与弹性系数ks的乘积对应浮子受到的等效弹簧阻力fs(t)；利用wamit软件计算得方程所涉及的水动力参数(包括浮子质量m、浮子附加质量m
add
、阻尼系数k(t)和弹性系数ks)；f
wave
为作为输入的波浪激励力；f
pto
为来自系统动力输出装置(power take-off，pto)的外加电磁推力。
[0039]
为了提高控制过程的计算效率，本发明采用状态空间模型近似替代机械运动模型表达式中的辐射力fr(t)卷积项，转换的过程如下：
[0040]
先使用prony算法拟合k(t)曲线，得到其复指数加权和的形式，再经过拉氏变换得到辐射系数的s域表达式，然后采用平衡截断法对上式进行降阶，求得参数ar∈r4×4、br∈r4×1，cr∈r1×4和dr∈r1×1，得到fr(t)的四阶状态空间模型，表达形式如下：
[0041][0042]
式中，xr(t)∈r4×1，它没有实际物理意义，只是表示状态空间模型中的状态变量；z(t)表示浮子的位移，其微分项即为浮子的运动速度，
[0043]
步骤2、建立直驱式波浪发电系统的直线永磁电机模型：
[0044]
建立直线永磁电机在a-b-c坐标系下的定子端电压方程，表达式如下
[0045][0046]
式中，u
s_abc
为定子端的电压向量；r＝diag(rs,rs,rs)，rs为定子绕组的电阻；l为定子电感矩阵；i
abc
为定子绕组电流向量；ψ
pm_abc
为永磁体转子在定子中产生的磁链；
[0047]
将静止a-b-c坐标系转化为d-q旋转坐标系，获得dq轴电压平衡方程如下：
[0048][0049]
式中，ω为直线永磁电机的电角速度，ω＝2πv/λ，λ为电机的极距；id为定子d轴电流，iq为定子q轴电流，m为定子绕组之间的互感，l
ss
为定子绕组的自感，ls＝l
ss-m；
[0050]
根据直线永磁电机各参量之间的关系，推导得到q轴电流i
qs
与pto力f
pto
的线性关系式：
[0051][0052]
步骤3、建立基于模型预测控制的直驱式波浪发电系统状态空间模型：
[0053]
建立波浪发电系统装置运动方程等价表达式，如下
[0054][0055]
式中，代表缩放后的波浪激励力；作为系统的控制量；获得控制量uq(t)和定子q轴电流i
qs
(t)的关系式如下：
[0056][0057]
以浮子的升沉位移z(t)、运动速度和中间量xr(t)作为状态变量，获得波浪发电系统的连续状态空间模型如下：
[0058][0059]
其中，系数矩阵为：
[0060][0061]
步骤4、建立模型预测控制的目标函数，搭建离散状态空间模型：
[0062]
基于直驱式波浪发电系统控制目标，建立包含pto力f
pto
惩罚项的功率优化目标函数，形式如下：
[0063][0064]
基于目标函数，结合考虑弱磁控制的直驱式波浪发电系统的工作原理，将控制量uq(t)、缩放后的波浪激励力v(t)、速度变化量和d轴电流id(t)作为新加入的状态量，对模型进行增广，并转换到离散域，最终得到系统的离散状态空间模型：
[0065][0066]
式中系数矩阵为：
[0067][0068][0069][0070]
式中，υ＝[0 1 0]，t
l
为采样间隔，ac、bc、fc分别为步骤3中所得连续状态空间模型的系数矩阵。
[0071]
步骤5、状态量的滚动优化：
[0072]
迭代k时刻起始的未来n步时域内的输出序列进行状态量的滚动预测，表达式如下：
[0073][0074]
式中，
[0075][0076][0077][0078][0079]
x(k)表示k时刻处的系统状态变量，表示缩放波浪力在k时刻起始的未来n步增量序列。
[0080]
仅取第一个增量作用于系统，得到下一时刻的控制量：
[0081]
u(k)＝δu(k)+u(k-1)
[0082]
重复上述过程直至完成滚动预测控制，实现系统的在线优化求解。
[0083]
步骤6、约束条件：
[0084]
在控制过程中将直驱式波浪发电系统的物理限制纳入算法的约束中，其中线性约束包括浮子的升沉位移z(t)、运动速度和pto力f
pto
，表达式如下：
[0085][0086]
非线性约束包括定子电压幅值、定子电流幅值和弱磁率τ。其中，定子电压幅值极限值u
max
取决于pwm整流器直流侧电压，在spwm的脉宽调制方式下为直流母线电压u
dc
的1/2；定子电流幅值极限值i
max
取决于电机温升和pwm整流器输出容量的限制；还需特别指出的是，在永磁电机实际弱磁运行过程中，若直轴去磁电流过大，会导致永磁体面临永久退磁的危险，故应控制弱磁率τ始终小于等于1，其中弱磁率τ的定义式如下：
[0087][0088]
由此可总结得非线性约束的表达式如下：
[0089][0090]
由此可得受非线性约束的定子电流运行范围示意图如图3所示，当发电机处于低速区，在id＝0控制下定子电流矢量位于iq轴上，此时满足最大功率捕获所需的fpto1对应的电流参考值i
qref
始终位于电流极限圆和电压极限圆内，如点a所示；随动子速度升高，电压极限环收缩，所需fpto2对应电流参考值与电压极限圆相交，处于临界状态，如点b所示；动子速度进一步升高，电压极限圆收缩，所需fpto3对应电流参考值与q轴交点位于极限圆之外，故此时应增大直轴电流参考值i
dref
，工作点向右移动直至满足限制条件，如点c所示，电流矢量控制由id＝0控制切换为弱磁控制。
[0091]
综上所述，本发明能够在满足系统约束的情况下，提高直驱式波浪发电系统的功率捕获性能，并采用id＝0控制与弱磁控制结合的定子电流矢量控制方式，有效拓宽永磁直线发电机的运行速域，提高系统运行的稳定性。