一种永磁同步电机自适应积分滑模预测控制方法

1.本发明属于永磁同步电机控制技术领域，特别涉及基于bp神经网络和参数自调节的永磁同步电机双闭环控制技术。


背景技术：

2.永磁同步电机控制中对于系统的稳定性、控制精度、动态响应速度以及抗干扰能力等性能均具有较高的要求，矢量控制是现有永磁同步电机调速系统中应用较广泛的手段，其中目前最常用的是转速环和电流环双闭环控制策略。然而，这种矢量控制策略仍然存在一些缺陷，譬如在闭环控制中被较多使用的pi线性控制，其控制动态性能和控制精度较差；而基于滑模控制的非线性策略也会由于系统状态始终在滑模面附近来回颤动，而存在抖振问题。此外，控制参数直接影响着控制器的性能，不同工况对应的控制参数也不同，因此无论是线性或非线性控制策略都存在参数整定复杂的弊端。


技术实现要素：

3.有鉴于此，针对上述本领域中存在的技术问题，本发明提供了一种永磁同步电机自适应积分滑模预测控制方法，具体包括以下步骤：
4.步骤一、构建永磁同步电机的等效数学模型，并针对转速环和电流环先后建立自适应积分滑模预测控制器模型，转速环和电流环滑模面均可表示为：
[0005][0006]
式中，s(t)和e(t)分别为t时刻的滑模面和跟踪误差；c表示积分增益系数且c＞0；
[0007]
且采用以下指数趋近律：
[0008][0009]
其中，趋近律系数q＞0、ε＞0，上标
·
表示对应参数的一阶导数；
[0010]
步骤二、在转速环的滑模预测控制器模型中，对转速环s
ω
滑模面的一阶导数引入自适应因子，改进为以下形式：
[0011][0012]
其中，c
ω
为转速环滑模面的积分增益系数且c
ω
＞0，ωm为转子机械角速度，上标*表示对应参数的参考值；
[0013]
步骤三、选择在不同目标转速和负载转矩下使控制性能达到最优的转速环滑模预测控制器模型的控制参数：积分增益系数c
ω
、趋近律系数q
ω
和λ，与对应的目标转速和负载转矩共同组建训练集对bp神经网络进行训练；所述bp神经网络以目标转速和负载转矩作为输入层节点，c
ω
、q
ω
和λ作为输出层节点；
[0014]
步骤四、利用训练好的bp神经网络结合转速环和电流环的滑模预测控制器模型，
实现转速环的参数自适应调节及控制。
[0015]
进一步地，步骤一中对于永磁同步电机具体建立以下旋转坐标系下的电压方程：
[0016][0017]
式中，ud和uq分别为d、q轴定子电压分量；id和iq分别为d、q轴定子电流分量；rs，ls和ψf分别为定子电阻、定子电感和转子永磁体磁链，ωe为电角速度；t为时间变量；
[0018]
以及建立以下电磁转矩方程和动力学方程：
[0019][0020]
式中，te为电磁转矩；p为极对数，t
l
为负载转矩；b为粘滞摩擦系数，j为转子转动惯量；
[0021]
则利用一阶前向欧拉公式离散化后，转速环的滑模预测控制器模型具体形式为：
[0022][0023]
式中，r
ωlaw
表示转速环滑模预测控制器模型的自适应趋近律；t为转速环控制周期；
[0024]
电流环的滑模预测控制器模型具体形式为：
[0025][0026]
其中，s
d,q
为电流环控制器d、q轴定子电流的滑模面，c
d,q
为电流环滑模面的积分增益系数且c
d,q
》0，r
d,qlaw
表示电流环滑模控制器的自适应趋近律，q
d,q
为趋近律系数且q
d,q
＞0，ts为电流环控制周期。
[0027]
进一步地，转速环的滑模预测控制器模型中，其滑模面具体为以下形式：
[0028]
[0029][0030]
式中，上标..表示对应参数的二阶导数，下标ω为转速环对应的各参数；
[0031]
电流环的滑模预测控制器模型中，其滑模面具体为以下形式：
[0032][0033][0034]
式中，下标d和q为电流环对应的d轴、q轴各参数。
[0035]
进一步地，步骤三所述bp神经网络的具体训练过程包括：
[0036]
a.选取不同目标转速和负载转矩下的最优控制参数，构建包括训练样本与测试样本的训练集；
[0037]
b.训练样本数据归一化；
[0038]
c.构建bp神经网络模型，设置训练次数、学习速率、训练目标最小误差等参数，隐含层节点设置为5，设置权重和偏置的初始值；
[0039]
d.测试样本归一化；
[0040]
e.利用bp神经网络对测试样本进行预测；
[0041]
f.将预测结果反归一化并与真实值进行比较；
[0042]
g.若预测结果符合预期误差，则结束训练，输出神经网络的权重和偏置，得到训练好的bp神经网络；否则更新权重和偏置，重复步骤d-g直至完成训练。
[0043]
进一步地，步骤四中利用训练好的bp神经网络，首先输入目标转速和负载转矩并输出最优的参数c
ω
、q
ω
和λ；
[0044]
再将上述参数c
ω
、q
ω
和λ输入建立的滑模预测控制器模型，并完成转速环的参数自适应调节及控制。
[0045]
上述本发明所提供的永磁同步电机自适应积分滑模预测控制方法，通过构建转速环与电流环的自适应积分滑模预测控制模型，并对其中的转速环部分引入自适应因子进行改进，再利用运行工况和最优控制参数训练bp神经网络，实现了转速环控制器的自适应调节控制，从而能够有效克服现有技术中控制器参数整定不便的缺陷，并显著双闭环控制策略的动态控制性能。
附图说明
[0046]
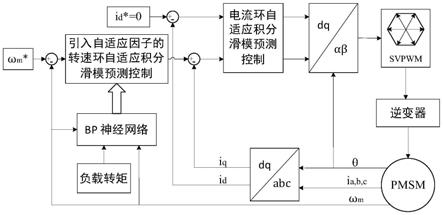
图1为本发明所提供方法的控制系统框架示意图；
[0047]
图2为本发明所提供方法中对bp神经网络训练的流程图；
[0048]
图3为现有技术中对转速和电流控制的效果图
[0049]
图4为基于本发明的实例中对转速和电流控制的效果图。
具体实施方式
[0050]
下面将结合附图对本发明的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0051]
本发明所提供的一种永磁同步电机自适应积分滑模预测控制方法，如图1所示，具体包括以下步骤：
[0052]
步骤一、构建永磁同步电机的等效数学模型，并针对转速环和电流环先后建立自适应积分滑模预测控制器模型，转速环和电流环滑模面均可表示为：
[0053][0054]
式中，s(t)和e(t)分别为t时刻的滑模面和跟踪误差；c表示积分增益系数且c＞0；
[0055]
指数趋近律表达式如下：
[0056][0057]
其中，趋近律系数q＞0、ε＞0。
[0058]
采用一阶前向欧拉对积分滑模面进行离散化，结合指数趋近律可得：
[0059][0060]
推导得到s(t+t)表达式为：
[0061]
s(t+t)＝m[s(t)]
[0062]
其中，
[0063]
滑模面s(t)递减的充分条件是∣m∣《1，即：
[0064][0065]
取且得到以下自适应滑模趋近律：
[0066][0067]
上标
·
表示对应参数的一阶导数；
[0068]
步骤二、在转速环的滑模预测控制器模型中，对转速环s
ω
滑模面的一阶导数引入自适应因子，改进为以下形式：
[0069][0070]
其中，c
ω
为转速环滑模面的积分增益系数且c
ω
＞0，ωm为转子机械角速度，上标*表示对应参数的参考值；
[0071]
步骤三、选择在不同目标转速和负载转矩下使控制性能达到最优的转速环滑模预测控制器模型的控制参数：积分增益系数c
ω
、趋近律系数q
ω
和λ，与对应的目标转速和负载转矩共同组建训练集对bp神经网络进行训练；所述bp神经网络以目标转速和负载转矩作为
输入层节点，c
ω
、q
ω
和λ作为输出层节点；
[0072]
步骤四、利用训练好的bp神经网络结合转速环和电流环的滑模预测控制器模型，实现转速环的参数自适应调节及控制。
[0073]
在本发明的一个优选实施方式中，步骤一中对于永磁同步电机具体建立以下旋转坐标系下的电压方程：
[0074][0075]
式中，ud和uq分别为d、q轴定子电压分量；id和iq分别为d、q轴定子电流分量；rs，ls和ψf分别为定子电阻、定子电感和转子永磁体磁链，ωe为电角速度；t为时间变量；
[0076]
以及建立以下电磁转矩方程和动力学方程：
[0077][0078]
式中，te为电磁转矩；p为极对数，t
l
为负载转矩；b为粘滞摩擦系数，j为转子转动惯量；
[0079]
则利用一阶前向欧拉公式离散化后，转速环的滑模预测控制器模型具体形式为：
[0080][0081]
式中，r
ωlaw
表示转速环滑模预测控制器模型的自适应趋近律；t为转速环控制周期；
[0082]
电流环的滑模预测控制器模型具体形式为：
[0083][0084]
其中，s
d,q
为电流环控制器d、q轴定子电流的滑模面，c
d,q
为电流环滑模面的积分增益系数且c
d,q
》0，r
d,qlaw
表示电流环滑模控制器的自适应趋近律，q
d,q
为趋近律系数且q
d,q
＞0，ts为电流环控制周期。
[0085]
在本发明的一个优选实施方式中，转速环的滑模预测控制器模型中，其滑模面具体为以下形式：
[0086][0087][0088]
式中，上标
··
表示对应参数的二阶导数，下标ω为转速环对应的各参数；
[0089]
电流环的滑模预测控制器模型中，其滑模面具体为以下形式：
[0090][0091][0092]
式中，下标d和q为电流环对应的d轴、q轴各参数。
[0093]
在本发明的一个优选实施方式中，步骤三所述bp神经网络的训练具体过程如图2所示，包括：
[0094]
a.选取不同目标转速和负载转矩下的最优控制参数，构建包括训练样本与测试样本的训练集；
[0095]
b.训练样本数据归一化；
[0096]
c.构建bp神经网络模型，设置训练次数、学习速率、训练目标最小误差等参数，隐含层节点设置为5，设置权重和偏置的初始值；
[0097]
d.测试样本归一化；
[0098]
e.利用bp神经网络对测试样本进行预测；
[0099]
f.将预测结果反归一化并与真实值进行比较；
[0100]
g.若预测结果符合预期误差，则结束训练，输出神经网络的权重和偏置，得到训练好的bp神经网络；否则更新权重和偏置，重复步骤d-g直至完成训练。
[0101]
在本发明的一个优选实施方式中，步骤四中利用训练好的bp神经网络，首先输入目标转速和负载转矩并输出最优的参数c
ω
、q
ω
和λ；
[0102]
再将上述参数c
ω
、q
ω
和λ输入建立的滑模预测控制器模型，并完成转速环的参数自适应调节及控制。
[0103]
附图3和附图4分别示出了未引入自适应因子与bp神经网络的现有控制策略与基于本发明的控制策略的转速和电流控制效果对比。其中，转速环控制周期为500μs，电流环控制周期为50μs。两者实验工况相同，包括电机带载3nm启动至转速为850rpm(图3左和图4左)以及电机带载5nm启动至转速为400rpm(图3右和图4右)。实验结果表明，改进前的控制策略由于控制参数与复杂多变的实际运行工况不匹配，导致电流动态响应速度慢且稳定性差，稳态运行时转速和电流波动较大，而改进后的控制策略不受运行工况的限制，可以自动调节至最优控制参数，增强了控制器的鲁棒性，保证了各种工况下电机的动态响应性能和
稳态性能。
[0104]
应理解，本发明实施例中各步骤的序号的大小并不意味着执行顺序的先后，各过程的执行顺序应以其功能和内在逻辑确定，而不应对本发明实施例的实施过程构成任何限定。
[0105]
尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定。