一种柔性直流电网的稳定性分析方法及装置与流程

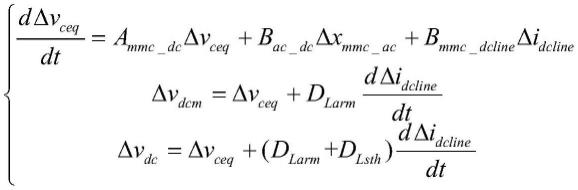
1.本发明涉柔性直流电网仿真技术领域，具体涉及一种柔性直流电网的稳定性分析方法及 装置。


背景技术：

2.近年来，基于全控型器件的电压源换流器直流输电技术(voltage source converter basedhvdc，vsc-hvdc)发展迅速，已成为实现大规模新能源接入，输电系统高可控性和灵活 性的一种有效手段。其中，基于模块化多电平换流器的直流输电技术(modular multilevelconverter based hvdc，mmc-hvdc)因其低谐波含量、可扩展性等优势在高压大容量柔性 直流输电工程中广泛应用。
3.柔性直流电网是由多个电压源型换流器互联构成，以直流方式进行电能传输的电力网 络。柔性直流电网不仅具备双端柔性直流系统快速、灵活可控等技术特点，还可以最大限度 的综合各种新能源、负荷的分布特性进行多元互补，因此已经成为当前电力系统的研究热点。 目前，已经建设完成了张北
±
500kv四端柔性直流电网示范工程，将对张北地区的大规模可 再生能源汇集消纳发挥重要作用，在全世界范首次实现了大规模可再生能源经直流电网向特 大城市供电。世界范围内，欧洲及美国等电网发展规划都对柔性直流输电技术提出了建设规 划，特别是欧洲国家在原先智能电网概念的基础上提出了超级电网计划，本质上都是基于模 块化多电平换流器或类似拓扑构建成柔性直流电网。
4.柔性直流电网的发展建设将使电网呈现越来越强烈的交直流相互耦合、暂态过程复杂多 变的特性，对系统分析提出了严峻的挑战。柔性直流动态行为及控制环节较为复杂，系统运 行方式的变化、功率参考值的变化以及其他外部因素的干扰均有可能引发系统振荡甚至失稳 现象，国内外多个柔性直流输电工程在调试或运行阶段发生振荡现象，振荡频率覆盖低、中 和高频段。为揭示系统耦合振荡的机理，需要建立柔性直流电网的小信号模型及稳定性分析 理论，探讨主电路参数和控制环节对系统稳定性的影响规律，揭示系统振荡模式及模态特征， 从而为构建振荡源辨识方法并提出有效的振荡抑制措施提供理论依据。


技术实现要素：

5.为了克服上述缺陷，本发明提出了一种柔性直流电网的稳定性分析方法及装置。
6.第一方面，提供一种柔性直流电网的稳定性分析方法，所述柔性直流电网的稳定性分析 方法包括：
7.利用预先确定的柔性直流电网的小干扰模型进行仿真；
8.在仿真系统中对柔性直流电网进行小干扰稳定性分析。
9.优选的，所述预先确定的柔性直流电网的小干扰模型的确定过程包括：
10.建立柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模型和 柔性直流电网直流线路小干扰模型；
11.基于所述柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模 型和柔性直流电网直流线路小干扰模型确定柔性直流电网的小干扰模型。
12.进一步的，所述柔性直流电网换流器对应的交流侧小干扰模型的数学模型如下：
[0013][0014]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号，a
mmc_ac
为柔性直流 电网换流器对应的状态矩阵信号向量，
△
x
mmc_ac
为柔性直流电网换流器对应的状态变量矩阵信 号向量，bu为柔性直流电网换流器对应的第一输入矩阵，
△uref
为柔性直流电网换流器对应 的输入变量矩阵信号向量，b
dc_ac
为柔性直流电网换流器对应的第二输入矩阵，
△vdcm
为柔性 直流电网换流器对应的测量点的直流电压信号。
[0015]
进一步的，所述柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电网换 流器对应的交流侧小干扰信号的数学模型如下：
[0016][0017]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电 网换流器对应的交流侧小干扰信号，
△
id为交流侧电流的d轴分量信号，
△iq
为交流侧电流的 q轴分量信号，
△vcd
为阀侧电压的d轴分量信号，
△vcq
为阀侧电压的q轴分量信号，
△
θ为锁 相环输出的相角信号，
△
x
ω
为pcc点电压q轴分量的积分信号，
△
x
p
为有功功率给定值与实测 值偏差的积分信号，
△
x
dc
为直流电压实测值与给定值偏差的积分信号，
△
xq为无功功率给定值 与实测值偏差的积分信号，
△
x
id
为交流电流d轴分量给定值与实测值偏差的积分信号，
△
x
iq
为 交流电流q轴分量给定值与实测值偏差的积分信号，t为转置符号。
[0018]
进一步的，对于定有功功率换流站，所述柔性直流电网换流器对应的状态矩阵信号向量 中第m个换流器对应的状态矩阵信号的数学模型如下：
[0019][0020]
所述柔性直流电网换流器对应的第一输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0021][0022]
所述柔性直流电网换流器对应的第二输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0023][0024]
上式中，ω0为锁相环输出的初始角速度，为电流内环控制比例控制系数，为电流 内环控制积分控制系数，di为电流内环控制解耦系数，为有功功率外环控制比例控制系数，为有功功率外环控制积分控制系数，为无功功率外环控制比例控制系数，为无功功率 外环控制积分控制系数，为锁相环比例控制系数，为锁相环积分控制系数，v
pd
为pcc 点电压的d轴分量，v
pq
为pcc点电压的q轴分量，id为交流电流d轴分量，iq为交流电流q 轴分量，tc为阀基控制系统等效惯性环节时间常数，ls为交流系统等效阻抗，lc为柔直换流 器交流侧等效阻抗，vs为交流系统等效理想电源电压，θ0为锁相环输出的初始锁相角，v
cdref
为换流器输出的阀侧电压d分量参考值，v
dcrate
为额定直流电压，lc＝l
t
+l
arm
/2，l
t
为换 流变压器漏抗，l
arm
为换流器桥臂电抗，v
cqref
为换流器输出的阀侧电压q分量参考值。
[0025]
进一步的，对于定直流电压换流站，所述柔性直流电网换流器对应的状态矩阵信号向量 中第m个换流器对应的状态矩阵信号的数学模型如下：
[0026][0027]
所述柔性直流电网换流器对应的第一输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0028][0029]
所述柔性直流电网换流器对应的第二输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0030][0031]
上式中，为直流电网外环控制比例控制系数，为直流电网外环控制积分控制系数。
[0032]
进一步的，所述柔性直流电网换流器直流侧小干扰模型的数学模型如下：
[0033][0034]
上式中，
△vceq
为换流器直流侧等效电容电压信号，a
mmc_dc
为柔性直流电网换流器直流侧 的状态矩阵信号向量，b
ac_dc
为柔性直流电网换流器直流侧的第一输入矩阵，b
mmc_dcline
为柔性 直流电网换流器直流侧的第二输入矩阵，
△idcline
为直流线路电流信号，
△vdcm
为测量点的直流 电压信号，d
larm
为与柔性直流电网拓扑相关的桥臂电感矩阵，
△vdc
为测量点的平波电抗器后 的直流电压信号，d
lsth
为与柔性直流电网拓扑相关的平波电抗矩阵；
[0035]
其中，所述柔性直流电网换流器直流侧的状态矩阵信号向量的数学模型为：
[0036][0037]
所述柔性直流电网换流器直流侧的第一输入矩阵的数学模型为：
[0038][0039]
所述柔性直流电网换流器直流侧的第一输入矩阵中第m行第m列个元素的计算式为：
[0040]
[0041]
所述柔性直流电网换流器对应的第二输入矩阵的数学模型为：
[0042][0043]
所述与柔性直流电网拓扑相关的桥臂电感矩阵的数学模型如下：
[0044][0045]
所述与柔性直流电网拓扑相关的平波电抗矩阵的数学模型如下：
[0046][0047]
上式中，为柔性直流电网第m个换流器交流侧电压d轴分量，为柔性直流电网第 m个换流器交流侧电压q轴分量，为柔性直流电网第m个换流器直流侧等效电容， 为柔性直流电网第m个换流器子模块电容，n为柔性直流电网第m个换 流器桥臂子模块数，为柔性直流电网第m个换流器直流侧等效电容电压，为柔性直 流电网第m个换流器交直流侧电气量的关联矩阵，为柔性直流电网第m个换流器桥臂电 感，为柔性直流电网第m个换流器直流侧电流与直流网络线路电流的关系矩阵，为 柔性直流电网第m个换流器平波电抗。
[0048]
进一步的，所述柔性直流电网直流线路小干扰模型的数学模型如下：
[0049][0050]
上式中，
△vline
为直流线路等效电容电压，
△idcline
为直流线路电流信号，b
line_i
为表征换流 器在直流电网中相对位置的关联矩阵，a
line_i
为直流线路等效电感矩阵，a
line_v
为直流线路等 效电容矩阵，
△vdc
为测量点的平波电抗器后的直流电压信号；
[0051]
所述直流线路等效电容矩阵的数学模型如下：
[0052][0053]
所述直流线路等效电感矩阵的数学模型如下：
[0054][0055]
上式中，为第n条直流线路的等效集中电容值，为第n条直流线路的等效集中 电感值。
[0056]
进一步的，所述柔性直流电网的小干扰模型的数学模型如下：
[0057][0058]
上式中，为柔性直流电网的小干扰信号，a
sys
为柔性直流电网的状态矩阵信号向量，
ꢀ△
x
sys
为柔性直流电网的状态变量矩阵信号向量，b
sys
为柔性直流电网的输入矩阵；
[0059]
其中，所述柔性直流电网的状态变量矩阵信号向量的数学模型如下：
[0060][0061]
所述柔性直流电网的状态矩阵信号向量的数学模型如下：
[0062][0063]
所述柔性直流电网的输入矩阵的数学模型如下：
[0064][0065]
上式中，t为转置符号，e
2n
×
2n
为2n
×
2n的单位矩阵，n为直流线路总条数，a
dcline
为第 一中间变量，a
dcline
＝[e
2n
×
2n-b
line_i
(d
larm
+d
lsth
)]-1aline_i
，b
dcline
为第二中间变量， b
dcline
＝[e
2n
×
2n-b
line_i
(d
larm
+d
lsth
)]-1bline_i
，em×m为m
×
m的单位矩阵。
[0066]
第二方面，提供一种柔性直流电网的稳定性分析装置，所述柔性直流电网的稳定性分析 装置包括：
[0067]
仿真模块，用于利用预先确定的柔性直流电网的小干扰模型进行仿真；
[0068]
分析模块，用于在仿真系统中对柔性直流电网进行小干扰稳定性分析。
[0069]
优选的，所述仿真模块中，预先确定的柔性直流电网的小干扰模型的确定过程包括：
[0070]
建立柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模型和 柔性直流电网直流线路小干扰模型；
[0071]
基于所述柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模 型和柔性直流电网直流线路小干扰模型确定柔性直流电网的小干扰模型。
[0072]
进一步的，所述柔性直流电网换流器对应的交流侧小干扰模型的数学模型如下：
[0073][0074]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号，a
mmc_ac
为柔性直流 电网换流器对应的状态矩阵信号向量，
△
x
mmc_ac
为柔性直流电网换流器对应的状态变量矩阵信 号向量，bu为柔性直流电网换流器对应的第一输入矩阵，
△uref
为柔性直流电网换流器对应 的输入变量矩阵信号向量，b
dc_ac
为柔性直流电网换流器对应的第二输入矩阵，
△vdcm
为柔性 直流电网换流器对应的测量点的直流电压信号。
[0075]
进一步的，所述柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电网换 流器对应的交流侧小干扰信号的数学模型如下：
[0076][0077]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电 网换流器对应的交流侧小干扰信号，
△
id为交流侧电流的d轴分量信号，
△iq
为交流侧电流的q轴分量信号，
△vcd
为阀侧电压的d轴分量信号，
△vcq
为阀侧电压的q轴分量信号，
△
θ为锁 相环输出的相角信号，
△
x
ω
为pcc点电压q轴分量的积分信号，
△
x
p
为有功功率给定值与实测 值偏差的积分信号，
△
x
dc
为直流电压实测值与给定值偏差的积分信号，
△
xq为无功功率给定值 与实测值偏差的积分信号，
△
x
id
为交流电流d轴分量给定值与实测值偏差的积分信号，
△
x
iq
为 交流电流q轴分量给定值与实测值偏差的积分信号，t为转置符号。
[0078]
进一步的，对于定有功功率换流站，所述柔性直流电网换流器对应的状态矩阵信号向量 中第m个换流器对应的状态矩阵信号的数学模型如下：
[0079][0080]
所述柔性直流电网换流器对应的第一输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0081][0082]
所述柔性直流电网换流器对应的第二输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0083][0084]
上式中，ω0为锁相环输出的初始角速度，为电流内环控制比例控制系数，为电流 内环控制积分控制系数，di为电流内环控制解耦系数，为有功功率外环控制比例控制系数，为有功功率外环控制积分控制系数，为无功功率外环控制比例控制系数，为无功功率 外环控制积分控制系数，为锁相环比例控制系数，为锁相环积分控制系数，v
pd
为pcc 点电压的d轴分量，v
pq
为pcc点电压的q轴分量，id为交流电流d轴分量，iq为交流电流q 轴分量，tc为阀基控制系统等效惯性环节时间常数，ls为交流系统等效阻抗，lc为柔直换流 器交流侧等效阻抗，vs为交流系统等效理想电源电压，θ0为锁相环输出的初始锁相角，v
cdref
为换流器输出的阀侧电压d分量参考值，v
dcrate
为额定直流电压，lc＝l
t
+l
arm
/2，l
t
为换 流变压器漏抗，l
arm
为换流器桥臂电抗，v
cqref
为换流器输出的阀侧电压q分量参考值。
[0085]
进一步的，对于定直流电压换流站，所述柔性直流电网换流器对应的状态矩阵信号向量 中第m个换流器对应的状态矩阵信号的数学模型如下：
[0086][0087]
所述柔性直流电网换流器对应的第一输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0088][0089]
所述柔性直流电网换流器对应的第二输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0090][0091]
上式中，为直流电网外环控制比例控制系数，为直流电网外环控制积分控制系数。
[0092]
进一步的，所述柔性直流电网换流器直流侧小干扰模型的数学模型如下：
[0093][0094]
上式中，
△vceq
为换流器直流侧等效电容电压信号，a
mmc_dc
为柔性直流电网换流器直流侧 的状态矩阵信号向量，b
ac_dc
为柔性直流电网换流器直流侧的第一输入矩阵，b
mmc_dcline
为柔性 直流电网换流器直流侧的第二输入矩阵，
△idcline
为直流线路电流信号，
△vdcm
为测量点的直流 电压信号，d
larm
为与柔性直流电网拓扑相关的桥臂电感矩阵，
△vdc
为测量点的平波电抗器后 的直流电压信号，d
lsth
为与柔性直流电网拓扑相关的平波电抗矩阵；
[0095]
其中，所述柔性直流电网换流器直流侧的状态矩阵信号向量的数学模型为：
[0096][0097]
所述柔性直流电网换流器直流侧的第一输入矩阵的数学模型为：
[0098][0099]
所述柔性直流电网换流器直流侧的第一输入矩阵中第m行第m列个元素的计算式为：
[0100]
[0101]
所述柔性直流电网换流器对应的第二输入矩阵的数学模型为：
[0102][0103]
所述与柔性直流电网拓扑相关的桥臂电感矩阵的数学模型如下：
[0104][0105]
所述与柔性直流电网拓扑相关的平波电抗矩阵的数学模型如下：
[0106][0107]
上式中，为柔性直流电网第m个换流器交流侧电压d轴分量，为柔性直流电网第 m个换流器交流侧电压q轴分量，为柔性直流电网第m个换流器直流侧等效电容， 为柔性直流电网第m个换流器子模块电容，n为柔性直流电网第m个换 流器桥臂子模块数，为柔性直流电网第m个换流器直流侧等效电容电压，为柔性直 流电网第m个换流器交直流侧电气量的关联矩阵，为柔性直流电网第m个换流器桥臂电 感，为柔性直流电网第m个换流器直流侧电流与直流网络线路电流的关系矩阵，为 柔性直流电网第m个换流器平波电抗。
[0108]
进一步的，所述柔性直流电网直流线路小干扰模型的数学模型如下：
[0109][0110]
上式中，
△vline
为直流线路等效电容电压，
△idcline
为直流线路电流信号，b
line_i
为表征换流 器在直流电网中相对位置的关联矩阵，a
line_i
为直流线路等效电感矩阵，a
line_v
为直流线路等 效电容矩阵，
△vdc
为测量点的平波电抗器后的直流电压信号；
[0111]
所述直流线路等效电容矩阵的数学模型如下：
[0112][0113]
所述直流线路等效电感矩阵的数学模型如下：
[0114][0115]
上式中，为第n条直流线路的等效集中电容值，为第n条直流线路的等效集中 电感值。
[0116]
进一步的，所述柔性直流电网的小干扰模型的数学模型如下：
[0117][0118]
上式中，为柔性直流电网的小干扰信号，a
sys
为柔性直流电网的状态矩阵信号向量，
ꢀ△
x
sys
为柔性直流电网的状态变量矩阵信号向量，b
sys
为柔性直流电网的输入矩阵；
[0119]
其中，所述柔性直流电网的状态变量矩阵信号向量的数学模型如下：
[0120][0121]
所述柔性直流电网的状态矩阵信号向量的数学模型如下：
[0122][0123]
所述柔性直流电网的输入矩阵的数学模型如下：
[0124][0125]
上式中，t为转置符号，e
2n
×
2n
为2n
×
2n的单位矩阵，n为直流线路总条数，a
dcline
为第 一中间变量，a
dcline
＝[e
2n
×
2n-b
line_i
(d
larm
+d
lsth
)]-1aline_i
，b
dcline
为第二中间变量， b
dcline
＝[e
2n
×
2n-b
line_i
(d
larm
+d
lsth
)]-1bline_i
，em×m为m
×
m的单位矩阵。
[0126]
第三方面，提供一种计算机设备，包括：一个或多个处理器；
[0127]
所述处理器，用于存储一个或多个程序；
[0128]
当所述一个或多个程序被所述一个或多个处理器执行时，实现所述的柔性直流电网的稳 定性分析方法。
[0129]
第四方面，提供一种计算机可读存储介质，其上存有计算机程序，所述计算机程序被执 行时，实现所述的柔性直流电网的稳定性分析方法。
[0130]
本发明上述一个或多个技术方案，至少具有如下一种或多种有益效果：
[0131]
本发明提供了一种柔性直流电网的稳定性分析方法及装置，包括：利用预先确定的柔性 直流电网的小干扰模型进行仿真；在仿真系统中对柔性直流电网进行小干扰稳定性分析。本 发明提供的技术方案，能够基于特征根法进行柔性直流电网的小干扰稳定分析，定位系统可 能存在的负阻尼或弱阻尼模态，并提取影响系统稳定性的关键因子；
[0132]
其中，本发明确定的柔性直流电网的小干扰模型具有模块化的建模特性，能够方便扩展 至任意端数、任意拓扑的柔性直流电网，并能够方便地在商业机电暂态仿真软件的小干扰分 析程序中实现。与电磁暂态pscad模型对比，本发明确定的柔性直流电网的小干扰模型在 柔性直流系统额定运行工况下，低频振荡模式的频率和阻尼比误差小于10％，能够适用于不 少于20个换流站的直流电网。
附图说明
[0133]
图1是本发明实施例的柔性直流电网的稳定性分析方法的主要步骤流程示意图；
[0134]
图2是本发明实施例的mmc直流侧动态模型；
[0135]
图3是本发明实施例的单条直流线路模型；
[0136]
图4是本发明实施例的柔性直流电网的稳定性分析装置的主要结构框图。
具体实施方式
[0137]
下面结合附图对本发明的具体实施方式作进一步的详细说明。
[0138]
为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附 图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明 一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有 做出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。
[0139]
如背景技术中所公开的，柔性直流电网是由多个电压源型换流器互联构成，以直流方式 进行电能传输的电力网络。柔性直流电网不仅具备双端柔性直流系统快速、灵活可控等技术 特点，还可以最大限度的综合各种新能源、负荷的分布特性进行多元互补，因此已经成为当 前电力系统的研究热点。目前，已经建设完成了张北
±
500kv四端柔性直流电网示范工程， 将对张北地区的大规模可再生能源汇集消纳发挥重要作用，在全世界范首次实现了大规模可 再生能源经直流电网向特大城市供电。世界范围内，欧洲及美国等电网发展规划都对柔性直 流输电技术提出了建设规划，特别是欧洲国家在原先智能电网概念的基础上提出了超级电网 计划，本质上都是基于模块化多电平换流器或类似拓扑构建成柔性直流电网。
[0140]
柔性直流电网的发展建设将使电网呈现越来越强烈的交直流相互耦合、暂态过程复杂多 变的特性，对系统分析提出了严峻的挑战。柔性直流动态行为及控制环节较为复杂，系统运 行方式的变化、功率参考值的变化以及其他外部因素的干扰均有可能引发系统振荡甚至失稳 现象，国内外多个柔性直流输电工程在调试或运行阶段发生振荡现象，振荡频率覆盖低、中 和高频段。为揭示系统耦合振荡的机理，需要建立柔性直流电网的小信号模型及稳定性分析 理论，探讨主电路参数和控制环节对系统稳定性的影响规律，揭示系统振荡模式及模态特征， 从而为构建振荡源辨识方法并提出有效的振荡抑制措施提供理论
依据。
[0141]
为了改善上述问题，本发明提供的一种柔性直流电网的稳定性分析方法及装置，包括： 利用预先确定的柔性直流电网的小干扰模型进行仿真；在仿真系统中对柔性直流电网进行小 干扰稳定性分析。本发明提供的技术方案，能够基于特征根法进行柔性直流电网的小干扰稳 定分析，定位系统可能存在的负阻尼或弱阻尼模态，并提取影响系统稳定性的关键因子；
[0142]
其中，本发明确定的柔性直流电网的小干扰模型具有模块化的建模特性，能够方便扩展 至任意端数、任意拓扑的柔性直流电网，并能够方便地在商业机电暂态仿真软件的小干扰分 析程序中实现。与电磁暂态pscad模型对比，本发明确定的柔性直流电网的小干扰模型在 柔性直流系统额定运行工况下，低频振荡模式的频率和阻尼比误差小于10％，能够适用于不 少于20个换流站的直流电网。下面对上述方案进行详细阐述。
[0143]
实施例1
[0144]
参阅附图1，图1是本发明的一个实施例的柔性直流电网的稳定性分析方法的主要步骤 流程示意图。如图1所示，本发明实施例中的柔性直流电网的稳定性分析方法主要包括以下 步骤：
[0145]
步骤s101：利用预先确定的柔性直流电网的小干扰模型进行仿真；
[0146]
步骤s102：在仿真系统中对柔性直流电网进行小干扰稳定性分析。
[0147]
本实施例中，所述步骤s102具体可以按下述方式执行：
[0148]
采用特征根分析法，求解预先确定的柔性直流电网的状态矩阵的特征根，分析特征根是 否处于复平面区域，若是，则柔性直流电网稳定，否则，柔性直流电网不稳定；
[0149]
具体的，所述预先确定的柔性直流电网的小干扰模型主要包括以下三个部分：(1)换流 器交流侧小干扰模型；(2)换流器直流侧小干扰模型；(3)直流线路小干扰模型。根据上述 各个部分的小干扰模型可以组合成任意端数、任意拓扑、考虑交流系统强弱特性的柔性直流 电网小干扰稳定模型。最后，基于影响因子和灵敏度分析提出了一种柔性直流电网稳定性的 评价方法，能够有效分析交直流电网弱阻尼的交互影响。
[0150]
在一个实施方式中，所述预先确定的柔性直流电网的小干扰模型的确定过程包括：
[0151]
建立柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模型和 柔性直流电网直流线路小干扰模型；
[0152]
基于所述柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模 型和柔性直流电网直流线路小干扰模型确定柔性直流电网的小干扰模型。
[0153]
其中，所述柔性直流电网换流器对应的交流侧小干扰模型的数学模型如下：
[0154][0155]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号，a
mmc_ac
为柔性直流 电网换流器对应的状态矩阵信号向量，
△
x
mmc_ac
为柔性直流电网换流器对应的状态变量矩阵信 号向量，bu为柔性直流电网换流器对应的第一输入矩阵，
△uref
为柔性直流电网换流器对应 的输入变量矩阵信号向量，b
dc_ac
为柔性直流电网换流器对应的第二输入矩阵，
△vdcm
为柔性 直流电网换流器对应的测量点的直流电压信号。
[0156]
其中，所述柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电网换流器 对应的交流侧小干扰信号的数学模型如下：
[0157][0158]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电 网换流器对应的交流侧小干扰信号，
△
id为交流侧电流的d轴分量信号，
△iq
为交流侧电流的 q轴分量信号，
△vcd
为阀侧电压的d轴分量信号，
△vcq
为阀侧电压的q轴分量信号，
△
θ为锁 相环输出的相角信号，
△
x
ω
为pcc点电压q轴分量的积分信号，
△
x
p
为有功功率给定值与实测 值偏差的积分信号，
△
x
dc
为直流电压实测值与给定值偏差的积分信号，
△
xq为无功功率给定值 与实测值偏差的积分信号，
△
x
id
为交流电流d轴分量给定值与实测值偏差的积分信号，
△
x
iq
为 交流电流q轴分量给定值与实测值偏差的积分信号，t为转置符号。
[0159]
具体的，对于定有功功率换流站，所述柔性直流电网换流器对应的状态矩阵信号向量中 第m个换流器对应的状态矩阵信号的数学模型如下：
[0160][0161]
所述柔性直流电网换流器对应的第一输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0162][0163]
所述柔性直流电网换流器对应的第二输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0164][0165]
上式中，ω0为锁相环输出的初始角速度，为电流内环控制比例控制系数，为电流 内环控制积分控制系数，di为电流内环控制解耦系数，为有功功率外环控制比例控制系数，为有功功率外环控制积分控制系数，为无功功率外环控制比例控制系数，为无功功率 外环控制积分控制系数，为锁相环比例控制系数，为锁相环积分控制系数，v
pd
为pcc 点电压的d轴分量，v
pq
为pcc点电压的q轴分量，id为交流电流d轴分量，iq为交流电流q 轴分量，tc为阀基控制系统等效惯性环节时间常数，ls为交流系统等效阻抗，lc为柔直换流 器交流侧等效阻抗，vs为交流系统等效理想电源电压，θ0为锁相环输出的初始锁相角，v
cdref
为换流器输出的阀侧电压d分量参考值，v
dcrate
为额定直流电压，lc＝l
t
+l
arm
/2，l
t
为换 流变压器漏抗，l
arm
为换流器桥臂电抗，v
cqref
为换流器输出的阀侧电压q分量参考值。
[0166]
对于定直流电压换流站，所述柔性直流电网换流器对应的状态矩阵信号向量中第m个换 流器对应的状态矩阵信号的数学模型如下：
[0167][0168]
所述柔性直流电网换流器对应的第一输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0169][0170]
所述柔性直流电网换流器对应的第二输入矩阵中第m个换流器对应的状态矩阵信号的数 学模型如下：
[0171][0172]
上式中，为直流电网外环控制比例控制系数，为直流电网外环控制积分控制系数。
[0173]
本实施例中，mmc内部动态特性较为复杂，子模块电容中的高频谐波特性在机电暂态 仿真软件中也难以模拟。因此，本发明主要关注柔性直流电网的外部动态特性，忽略换流器 内部的电磁暂态过程，通过交直流之间的功率耦合建立mmc直流侧平均值模型，如图2所 示。
[0174]
所述柔性直流电网换流器直流侧小干扰模型的数学模型如下：
[0175][0176]
上式中，
△vceq
为换流器直流侧等效电容电压信号，a
mmc_dc
为柔性直流电网换流器直流侧 的状态矩阵信号向量，b
ac_dc
为柔性直流电网换流器直流侧的第一输入矩阵，b
mmc_dcline
为柔性 直流电网换流器直流侧的第二输入矩阵，
△idcline
为直流线路电流信号，
△vdcm
为测量点的直流 电压信号，d
larm
为与柔性直流电网拓扑相关的桥臂电感矩阵，
△vdc
为测量点的平波电抗器后 的直流电压信号，d
lsth
为与柔性直流电网拓扑相关的平波电抗矩阵；
[0177]
其中，所述柔性直流电网换流器直流侧的状态矩阵信号向量的数学模型为：
[0178][0179]
所述柔性直流电网换流器直流侧的第一输入矩阵的数学模型为：
[0180]
[0181]
所述柔性直流电网换流器直流侧的第一输入矩阵中第m行第m列个元素的计算式为：
[0182][0183]
所述柔性直流电网换流器对应的第二输入矩阵的数学模型为：
[0184][0185]
所述与柔性直流电网拓扑相关的桥臂电感矩阵的数学模型如下：
[0186][0187]
所述与柔性直流电网拓扑相关的平波电抗矩阵的数学模型如下：
[0188][0189]
上式中，为柔性直流电网第m个换流器交流侧电压d轴分量，为柔性直流电网第 m个换流器交流侧电压q轴分量，为柔性直流电网第m个换流器直流侧等效电容， 为柔性直流电网第m个换流器子模块电容，n为柔性直流电网第m个换 流器桥臂子模块数，为柔性直流电网第m个换流器直流侧等效电容电压，为柔性直 流电网第m个换流器交直流侧电气量的关联矩阵，为柔性直流电网第m个换流器桥臂电 感，为柔性直流电网第m个换流器直流侧电流与直流网络线路电流的关系矩阵，为 柔性直流电网第m个换流器平波电抗。
[0190]
本实施例中，直流线路采用π型集中参数线路表示，如图3所示。π型线路的段数将决 定直流线路模拟频率的上限，理论上段数越多线路高频响应特性的模拟越精确。但是段数的 增加也会加大模型的阶数，降低模型的整体计算效率。另一方面，高频响应特性在机电暂态 仿真软件中难以模拟，单个π型线路已经能够满足直流线路在中低频段的模拟精度。因此， 综合考虑模拟精度和模型阶数，本发明选择单段π型线路来模拟直流线路。所述柔性直流电 网直流线路小干扰模型的数学模型如下：
[0191][0192]
上式中，
△vline
为直流线路等效电容电压，
△idcline
为直流线路电流信号，b
line_i
为表征换流 器在直流电网中相对位置的关联矩阵，a
line_i
为直流线路等效电感矩阵，a
line_v
为直流线路等 效电容矩阵，
△vdc
为测量点的平波电抗器后的直流电压信号；
[0193]
所述直流线路等效电容矩阵的数学模型如下：
[0194][0195]
所述直流线路等效电感矩阵的数学模型如下：
[0196][0197]
上式中，为第n条直流线路的等效集中电容值，为第n条直流线路的等效集中 电感值。
[0198]
综上，所述柔性直流电网的小干扰模型的数学模型如下：
[0199][0200]
上式中，为柔性直流电网的小干扰信号，a
sys
为柔性直流电网的状态矩阵信号向量，
ꢀ△
x
sys
为柔性直流电网的状态变量矩阵信号向量，b
sys
为柔性直流电网的输入矩阵；
[0201]
其中，所述柔性直流电网的状态变量矩阵信号向量的数学模型如下：
[0202][0203]
所述柔性直流电网的状态矩阵信号向量的数学模型如下：
[0204][0205]
所述柔性直流电网的输入矩阵的数学模型如下：
[0206][0207]
上式中，t为转置符号，e
2n
×
2n
为2n
×
2n的单位矩阵，n为直流线路总条数，a
dcline
为
第 一中间变量，a
dcline
＝[e
2n
×
2n-b
line_i
(d
larm
+d
lsth
)]-1aline_i
，b
dcline
为第二中间变量， b
dcline
＝[e
2n
×
2n-b
line_i
(d
larm
+d
lsth
)]-1bline_i
，em×m为m
×
m的单位矩阵。
[0208]
在一个最优的实施方式中，采用本发明提供的柔性直流电网的小干扰模型与电磁暂态 pscad模型对比，小干扰稳定模型在柔性直流系统额定运行工况下，低频振荡模式的频率和 阻尼比误差小于10％，能够适用于不少于20个换流站的直流电网。
[0209]
实施例2
[0210]
基于同一种发明构思，本发明还提供一种柔性直流电网的稳定性分析装置，如图4所示， 所述柔性直流电网的稳定性分析装置包括：
[0211]
仿真模块，用于利用预先确定的柔性直流电网的小干扰模型进行仿真；
[0212]
分析模块，用于在仿真系统中对柔性直流电网进行小干扰稳定性分析。
[0213]
优选的，所述仿真模块中，预先确定的柔性直流电网的小干扰模型的确定过程包括：
[0214]
建立柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模型和 柔性直流电网直流线路小干扰模型；
[0215]
基于所述柔性直流电网换流器交流侧小干扰模型、柔性直流电网换流器直流侧小干扰模 型和柔性直流电网直流线路小干扰模型确定柔性直流电网的小干扰模型。
[0216]
进一步的，所述柔性直流电网换流器对应的交流侧小干扰模型的数学模型如下：
[0217][0218]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号，a
mmc_ac
为柔性直流 电网换流器对应的状态矩阵信号向量，
△
x
mmc_ac
为柔性直流电网换流器对应的状态变量矩阵信 号向量，bu为柔性直流电网换流器对应的第一输入矩阵，
△uref
为柔性直流电网换流器对应 的输入变量矩阵信号向量，b
dc_ac
为柔性直流电网换流器对应的第二输入矩阵，
△vdcm
为柔性 直流电网换流器对应的测量点的直流电压信号。
[0219]
进一步的，所述柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电网换 流器对应的交流侧小干扰信号的数学模型如下：
[0220][0221]
上式中，为柔性直流电网换流器对应的交流侧小干扰信号中第m个柔性直流电 网换流器对应的交流侧小干扰信号，
△
id为交流侧电流的d轴分量信号，
△iq
为交流侧电流的 q轴分量信号，
△vcd
为阀侧电压的d轴分量信号，
△vcq
为阀侧电压的q轴分量信号，
△
θ为锁 相环输出的相角信号，
△
x
ω
为pcc点电压q轴分量的积分信号，
△
x
p
为有功功率给定值与实测 值偏差的积分信号，
△
x
dc
为直流电压实测值与给定值偏差的积分信号，
△
xq为无功功率给定值 与实测值偏差的积分信号，
△
x
id
为交流电流d轴分量给定值与实测值偏差的积分信号，
△
x
iq
为 交流电流q轴分量给定值与实测值偏差的积分信号，t为转置符号。
[0222]
进一步的，对于定有功功率换流站，所述柔性直流电网换流器对应的状态矩阵信号向量 中第m个换流器对应的状态矩阵信号的数学模型如下。