基于MFMA叠加调制的多频多负载MCR-WPT设计方法

基于mfma叠加调制的多频多负载mcr-wpt设计方法
技术领域
1.本发明涉及一种设计方法，尤其是一种基于mfma叠加调制的多频多负载mcr-wpt设计方法。


背景技术：

2.相比于传统有线电力的传输方式，无线电能传输技术的优势不言而喻，这种技术既方便又安全，人们一直希望能够摆脱对于有线电能传输方式的依赖。因此，无线电能传输技术的研究越来越深入，并且越来越多地被应用于现代社会的实际应用中，例如医学设备、电子设备、交通工具等领域。
3.当前wpt(wireless power transmission)技术日益普及，用户侧的设备需求也呈现出不同频率、功率等复杂多样的特点。基于无线充电联盟(wpc)提出qi充电标准的紧耦合感应技术以及基于airfuel组织的松散耦合磁谐振技术，已经被逐渐应用于多接收机wpt系统中，可以满足对于不同充电标准的负载设备供电需求。
4.根据接收机各自的谐振频率是否相同，多接收机wpt系统可分为单频多接收wpt系统和多频多接收wpt系统。多频多接收wpt系统已经逐渐成为目前多负载wpt系统研究的重点，该系统具有不同谐振频率的接收机；同时，发射机将与接收机谐振频率相同的频率混合输出，实现每个接收机与发射侧电源建立独立的功率传输通道的效果。
5.通过多频多接收wpt系统，可在发射侧就实现不同负载上的功率分配，即调节发射端相应频率的功率，也有助于减少接收线圈间的交叉耦合影响。现有多频多接收mcr-wpt(magnetically coupled resonant wireless power transfer，磁耦合谐振式无线电能传输)系统设计大部分采用多逆变器耦合至发射侧，体积与成本代价较大。
6.因此，设计体积小、成本低且不增加损耗的多频多负载mcr-wpt是目前急需解决的技术难题。


技术实现要素：

7.本发明的目的是克服现有技术中存在的不足，提供一种基于mfma叠加调制的多频多负载mcr-wpt设计方法，其所设计的多频多负载mcr-wpt，能够在单逆变器的基础上，实现多频多通道功率独立传输，工作在zcs状态，能有效降低成本与损耗。
8.按照本发明提供的技术方案，所述基于mfma叠加调制的多频多负载mcr-wpt设计方法，
9.构建一所需的多频多负载mcr-wpt系统，其中，所述多频多负载mcr-wpt系统包括发射基于mfma叠加调制混频信号的发射侧以及用于接收发射侧发射混频信号的接收侧，所述发射侧包括单逆变器以及一与所述单逆变器适配连接的发射回路，所述发射回路包括lcl补偿拓扑网络；所述接收侧包括n路相互独立的接收机，接收侧内的任一接收机耦合接收混频信号内与所述接收机谐振频率匹配的基频信号，以给连接至所述接收机的负载提供直流功率；
10.确定多频多负载mcr-wpt系统的零相位工作频率、系统基本参数以及目标工作频率，以根据所确定的零相位工作频率、系统基本参数以及目标工作频率构建适应度函数；
11.基于上述构建的适应度函数，寻优确定发射回路内lcl补偿拓扑网络的补偿网络参数，以在基于所确定补偿网络参数的发射回路下工作时，配置所述多频多负载mcr-wpt系统处于zcs状态。
12.所述单逆变器为基于氮化镓场效应管构建得到的逆变器；
13.发射回路包括n-2路lc谐振回路以及一lcl基本补偿网络，所述发射回路内的lc谐振回路依次适配连接，所述基本补偿网络包括发射线圈l
p
；
14.将n个待调制基频信号基于mfma叠加调制的混频信号发射输出时，n个接收机的谐振频率与mfma叠加调制n个基频信号的频率呈一一对应。
15.n个基频信号的频率完全不同，且任一基频信号的幅值独立可调。
16.采用基波分析法确定所述多频多负载mcr-wpt系统的电路模型矩阵，并根据所确定的电路模型矩阵得到总反射阻抗频率特性曲线，其中，对所得到的总反射阻抗频率特性曲线，利用图解法得到所述多频多负载mcr-wpt系统的零相位工作频率。
17.对任一接收机，包括耦合电感线圈以及不可控整流器，耦合电感线圈的两端分别通过一接收机回路导线电阻、一接收调谐电容与所述不可控整流器适配连接，以通过所述不可控整流器与负载适配连接，以给所述负载提供所需的直流功率。
18.确定的系统基本参数包括接收机的期望谐振频率f
ei
(i＝1,2,...,n)、发射线圈l
p
的电感、接收线圈l
si
的电感(i＝1,2,...,n)、发射线圈l
p
与各耦合电感线圈l
si
间互感m
psi
(i＝1,2,...,n)、接收机负载r
li
(i＝1,2,...,n)以及接收调谐电容c
si
(i＝1,2,...,n)。
19.根据零相位工作频率、系统基本参数以及目标工作频率构建适应度函数为：
[0020][0021]
其中，fitness为所构建的适应度函数，f
ei
表示第i个接收机的期望谐振频率，f
si
为系统第i个实际谐振频率，即系统第i个零相位工作频率，i
si
为第i个接收机的负载电流，i
sj
为第j个接收机负载电流，k
si
为系统输入阻抗角频率特性曲线在第i个实际谐振频率点处的导数，k
sj
为系统输入阻抗角频率特性曲线在第j个实际谐振频率点处的导数，w1为谐振频率的寻优权重系数、w2为负载电流的寻优权重系数与w3为谐振点系统输入阻抗角频率特性曲线导数的权重系数。
[0022]
对构建的适应度函数，基于pso方法寻优确定发射回路内lcl补偿拓扑网络的补偿网络参数，其中，确定补偿网络参数的过程包括如下步骤：
[0023]
步骤1、将发射回路内的发射谐振电感配置为电感粒子，将发射回路内的发射谐振电容配置为电容粒子，并确定第i个电感粒子l
fi
以及第i个电容粒子c
fi
相应的取值范围与运动速度范围，其中，i＝1,2,...,n-1；
[0024]
步骤2、随机初始化电感粒子l
fi
以及电容粒子c
fi
；
[0025]
步骤3、根据上述随机初始化后的电感粒子l
fi
以及电容粒子c
fi
，确定适应度函数的值，更新电感粒子l
fi
、电容粒子c
fi
相应的个体最佳适应度与群体最佳适应度；
[0026]
步骤4、根据上述更新电感粒子l
fi
、电容粒子c
fi
相应的个体最佳适应度与群体最佳适应度，更新电感粒子l
fi
、电容粒子c
fi
相对应的速度和位置，其中，
[0027][0028]
式中，l
mi
为电感粒子l
fi
个体最优粒子，y
lmi
为电感粒子l
fi
的群体最优粒子，li为电感粒子l
fi
当代种群所有粒子；c
mi
为电容粒子c
fi
个体最优粒子，y
cmi
为电容粒子c
fi
群体最优粒子，ci为电容粒子c
fi
当代种群所有粒子；β为惯性权重，λ1与λ2分别为自我学习因子和群体学习因子；rand为随机数产生器；
[0029]
步骤5、进行迭代次数控制，直至寻找到最佳适应度的电感粒子l
fi
与电容粒子c
fi
，以确定发射回路内lcl补偿拓扑网络的补偿网络参数。
[0030]
步骤1中，电感粒子l
fi
以及电容粒子c
fi
相应的取值范围与运动速度范围为：
[0031][0032][0033]
其中，vl
fi
为第i个电感粒子l
fi
的速度，vc
fi
为第i个电容粒子c
fi
相应的速度。
[0034]
基于mfma叠加调制的基频信号为正弦波信号；
[0035]
基于mfma叠加调制内基频信号的幅值为归一化幅值，对接收侧的多个接收机，与接收机所适配连接负载的直流功率与所述接收机所耦合基频信号的幅值呈一一对应。
[0036]
本发明的优点：构建多频多负载mcr-wpt系统时，发射侧发射基于mfma叠加调制混频信号，发射侧包括单逆变器以及一与所述单逆变器适配连接的发射回路，所述发射回路包括lcl补偿拓扑网络；
[0037]
采用mfma叠加调制法可解决现有多逆变器经变压器耦合至发射侧带来的高成本与高损耗问题；根据接收侧的接收机数量，发射侧采用合适的lcl拓扑补偿网络，从而可为多频多负载mcr-wpt系统带来相同数量的系统自然谐振频率，即可建立独立的功率通道进行传输；采用pso算法对基对系统谐振频率、负载电流与谐振点输入阻抗角频率特性曲线导数构建的适应度函数fitness进行寻优，从而可保证传输频率在各接收机的自然谐振频率点附近，且控制各负载接收功率保持平衡。
附图说明
[0038]
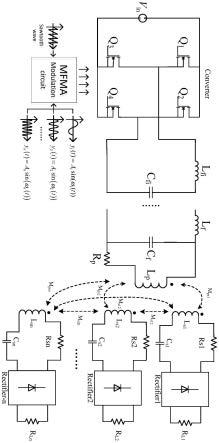
图1为本发明构建多频多负载mcr-wpt系统的电路原理图。
[0039]
图2为本发明构建双频双负载mcr-wpt系统的具体实施电路原理图。
[0040]
图3为图2中双频双负载mcr-wpt系统基于基波分析法建立等效电路模型的示意图。
[0041]
图4为图2中实施例的输入阻抗角与输入频率的关系图。
[0042]
图5为图3中实施例的输入阻抗与输入频率的关系图。
[0043]
图6为图2中实施例的双负载经输入端归一化电压幅值ai调节后负载电压的一种实施情况示意图。
[0044]
图7为图2中实施例的双负载经输入端归一化电压幅值ai调节后负载电压的另一种实施情况示意图。
[0045]
图8为图2中实施例的双负载经输入端归一化电压幅值ai调节后负载电压的第三种实施情况示意图。
[0046]
图9为图2中实施例的对双接收机经输入端归一化电压幅值ai调节后输出电压一种实施情况的fft分析图。
[0047]
图10为图2中实施例的对双接收机经输入端归一化电压幅值ai调节后输出电压另一种实施情况的fft分析图。
[0048]
图11中实施例的对双接收机经输入端归一化电压幅值ai调节后输出电压第三种实施情况的fft分析图。
具体实施方式
[0049]
下面结合具体附图和实施例对本发明作进一步说明。
[0050]
如图1所示：对所设计的多频多负载mcr-wpt，为了能够在单逆变器的基础上，实现多频多通道功率独立传输，工作在zcs状态，能有效降低成本与损耗，本发明基于mfma叠加调制的多频多负载mcr-wpt设计方法，具体地：
[0051]
构建一所需的多频多负载mcr-wpt系统，其中，所述多频多负载mcr-wpt系统包括发射基于mfma叠加调制混频信号的发射侧以及用于接收发射侧发射混频信号的接收侧，所述发射侧包括单逆变器以及一与所述单逆变器适配连接的发射回路，所述发射回路包括lcl补偿拓扑网络；所述接收侧包括n路相互独立的接收机，接收侧内的任一接收机耦合接收混频信号内与所述接收机谐振频率匹配的基频信号，以给连接至所述接收机的负载提供直流功率；
[0052]
确定多频多负载mcr-wpt系统的零相位工作频率、系统基本参数以及目标工作频率，以根据所确定的零相位工作频率、系统基本参数以及目标工作频率构建适应度函数；
[0053]
基于上述构建的适应度函数，寻优确定发射回路内lcl补偿拓扑网络的补偿网络参数，以在基于所确定补偿网络参数的发射回路下工作时，配置所述多频多负载mcr-wpt系统处于zcs状态。
[0054]
具体地，根据实际工作场景需求等构建一多频多负载mcr-wpt系统，与现有的mcr-wpt系统类似，所构建的mcr-wpt系统也包括发射侧以及与所述发射侧对应的接收侧，但与现有mcr-wpt不同的时，本发明所构建的mcr-wpt的发射侧能发射基于mfma(multi-frequency multi-amplitude多频率多幅值)叠加调制的混频信号，其中，发射侧包括单逆变器以及与所述单逆变器适配的发射回路，所述单逆变器即为一个逆变器，即本发明构建的多频多负载mcr-wpt系统中，发射侧包括一逆变器以及一与所述逆变器适配的发射回路。为了解决发射回路中没有补偿网络，增加损耗的问题，本发明实施例中，在发射回路内设置lcl补偿拓扑网络，即通过lcl补偿拓扑网络能减少损耗等问题。
[0055]
对所构建的mcr-wpt系统，接收侧可接收发射侧所发射的混频信号，接收侧一般可以包括n路相互独立的接收机，接收侧内接收机的路数n可以根据实际需要选择；n路接收机相互独立，具体是指每路接收机具有的谐振频率互不相同，任一路接收机在接收与谐振频率匹配的基频信号时，不会影响其他接收机对对应基频信号的接收。接收机的谐振频率与基频信号匹配，具体是指接收机的谐振频率与基频信号的频率相一致。具体工作时，任一接收机与一负载适配连接，从而在根据所接收到的基频信号实现给连接至所述接收机的负载
提供直流功率，接收机给负载提供直流功率的具体情况与现有相一致，具体提供直流功率的情况以能满足实际应用需求为准。
[0056]
具体实施时，对所构建的多频多负载mcr-wpt系统，接收侧接收机的工作参数等可以根据实际需要确定，即对构建的多频多负载mcr-wpt系统，需要确定发射侧内发射回路内lcl补偿拓扑网络的工作参数，以便使得多频多负载mcr-wpt系统能满足所需的工作状态需求，如配置多频多负载mcr-wpt系统处于zcs(zero-current switching、零电流开关)状态，多频多负载mcr
–
wpt系统处于zcs状态时，可减少开关损耗，通过谐振的方法，使开关关断时电子开关两端电流处于为零的状态，开关损耗接近于零。
[0057]
lcl补偿拓扑网络的工作参数即为lcl补偿拓扑网络的补偿网络参数。为了确定发射回路内lcl补偿拓扑网络的补偿网络参数，需要建立适应度函数，其中，建立适应度函数时，需要确定所述多频多负载mcr-wpt系统的零相位工作频率、系统基本参数以及目标工作频率。所述多频多负载mcr-wpt系统的零相位工作频率、系统基本参数以及目标工作频率的具体情况，下面进行具体解释说明。
[0058]
在建立适应度函数后，根据所构建的适应度函数，采用寻优方式确定发射回路内lcl补偿拓扑网络的补偿网络参数，当确定发射回路内lcl补偿拓扑网络的补偿网络参数后，即可确定的发射回路工作参数，在确定发射回路工作参数后，即实现多频多负载mcr-wpt系统的构建与设计。
[0059]
进一步地，所述单逆变器为基于氮化镓场效应管构建得到的逆变器；
[0060]
发射回路包括n-2路lc谐振回路以及一lcl基本补偿网络，所述发射回路内的lc谐振回路依次适配连接，所述基本补偿网络包括发射线圈l
p
；
[0061]
将n个待调制基频信号基于mfma叠加调制的混频信号发射输出时，n个接收机的谐振频率与mfma叠加调制n个基频信号的频率呈一一对应。
[0062]
本发明实施例中，单逆变器采用基于氮化镓场效应管构建的逆变器，即逆变器内的桥臂由氮化镓场效应管连接形成，逆变器内的桥臂采用基于氮化镓场效应管时，使得所形成的单逆变器具有更高的频率工作性能，导通损耗也较小。
[0063]
图1中，示出了单逆变器的一种具体实施情况，具体地，单逆变器包括nmos管q1、nmos管q2、nmos管q3以及nmos管q4，即nmos管q1、nmos管q2、nmos管q3以及nmos管q4均为氮化镓场效应管，nmos管q1的漏极端、nmos管q2的漏极端与信号源v
in
的正极端连接，nmos管q1的源极端与nmos管q3的漏极端连接，nmos管q2的源极端与nmos管q4的漏极端连接，nmos管q3的源极端以及nmos管q4的源极端均与信号源v
in
的连接端。
[0064]
对于发射回路，发射回路的一端与nmos管q1的源极端以及nmos管q3的漏极端连接，发射回路的另一端与nmos管q2的源极端以及nmos管q4的漏极端连接。
[0065]
对于发射回路，包括n-2路lc谐振回路以及一个lcl基本补偿回路，所述lcl基本补偿网络可为系统提供两个谐振频率，每增加一个lc谐振回路，即可为系统增加一个谐振频率。因此，当n-2个lc谐振回路与基本lcl补偿网络依次适配连接时，可为系统提供n个谐振频率，即实现n个不同频率通道的功率传输。
[0066]
图1中，l
p
为发射线圈，r
p
为基本补偿回路内的发射回路电阻，lc谐振回路内的电容为发射谐振电容，lc谐振回路内的电感为发射谐振电感，其中，发射谐振电容c
p1
与发射谐振电感l
f1
构成一路谐振lc谐振回路，发射谐振电感l
f1
的第一端、发射谐振电容c
p1
的第一端与
发射线圈l
p
的一端连接，发射线圈l
p
的另一端与发射回路电阻r
p
的一端连接，发射回路电阻r
p
的另一端与所有发射谐振电容的第二端以及nmos管q2所在的桥臂连接。
[0067]
具体实施时，lc谐振回路内发射谐振电容的第二端均与发射回路电阻r
p
以及nmos管q2所在的桥臂适配连接，发射谐振电容的第一端与形成lcl结构的发射谐振电感的端部适配连接，如发射谐振电容c
p1
的第一端与发射谐振电感l
f1
以及发射线圈l
p
连接，当存在发射谐振电容c
p2
时，所述发射谐振电容c
p2
的第一端与发射谐振电感l
f1
以及发射谐振电感l
f2
适配连接。
[0068]
具体地，当发射回路内存在多个lc谐振回路时，具体可以参考图1以及上述说明，此处不再赘述。
[0069]
发射侧发射基于mfma叠加调制混频信号时，即采用mfma叠加调制将n种不同频率、不同幅值的正弦波信号在时域上进行叠加，得到包含n种正弦波信息的混频信号，即基于mfma叠加调制的基频信号为正弦波信号，具体有：
[0070][0071]
其中，ω1≠ω2≠
…
≠ωn∈[ω
min
,ω
max
]，max|y(t)|≤y
max
，y1(t)、y2(t)、
…yn
(t)为n种不同频率、不同幅值的正弦波信号。为了方便后续分析与实验，a1，a2，
…
，an分别代表n种正弦波信号归一化后的电压幅值。
[0072]
具体实施时，混频信号可由外部的信号源产生，外部信号源所产生混频信号内基频信号的电压幅值可根据需要调节。为了能实现混频信号的传输，将包含n种基频信号的混频信号与高频三角载波进行比较，以根据比较结果分别输出高电平与低电平，以利用相应的高电平、低电平控制两对单逆变器内相应nmos管的导通状态，即根据单逆变器的导通状态，即可通过发射回路发射所需的混频信号。ω
min
、ω
max
具体可以根据实际需要选择确定，以能满足实际应用需求为准。
[0073]
图1和图2中，mfma modulation circuit即为实现上述对已基于mfma叠加的混频信号进行调制，得到互补方波控制信号的电路模块。具体地，高频三角波的频率需要大于最大输入电压信号频率的两倍；本发明实施例中，外部信号源产生混频信号，采用所述电路模块内的电压比较器实现混频信号与高频三角波的比较，将两种信号分别输入电压比较器的同相输入端与反向输入端，当混频信号的电压大于三角波电压时，输出高电平，否则，输出低电平。具体实施时，将得到的方波信号进行反相，由此得到一组互补的方波控制信号。所述方波信号包含混频信号里基频信号的幅值和频率信息，此时为控制信号。通过所述控制信号控制单逆变器内相应nmos开关管导通，将所述控制信号转化为功率信号，这个功率信号同样包含基频信号的幅值和频率信息，其电压幅值由输入单逆变器的直流电源v
in
决定。
[0074]
综上，即可实现生成基于mfma叠加调制的混频信号，混频信号经发射回路向所述多频多负载mcr-wpt系统的接收侧。
[0075]
具体地，任一基频信号的幅值独立可调，如第i个基频信号归一化电压幅值ai可以
单独调节，以调节对应谐振频率的第i个接收机的输出电压，从而实现各负载间功率独立分配。具体实施时，基频信号可以采用现有常用的技术手段实现电压幅值的调节，具体调节电压幅值的方式可以根据需要选择，以能满足电压幅值调节为准。是单逆变器实际输出相对应频率的电压的有效值，计算公式如下：
[0076][0077]
其中，a1，a2，
…
，an分别为n个基频信号归一化后的电压幅值，v
in
为直流电源的电源电压幅值。
[0078]
由上述说明可知，将n个待调制基频信号基于mfma叠加调制的混频信号发射输出时，n个接收机的谐振频率与mfma叠加调制n个基频信号的频率呈一一对应，即一接收机只接收与谐振频率相对应的基频信号。
[0079]
具体实施时，发射侧内发射混频信号内基频信号的传输频率在各接收机的自然谐振频率点附近，基于mfma叠加调制内基频信号的幅值为归一化幅值时，对接收侧的多个接收机，与接收机所适配连接负载的直流功率与所述接收机所耦合基频信号的幅值呈一一对应，即可实现各负载接收功率独立调节；其中，实现各负载接收功率独立调节，具体是指接收侧负载接收到的直流功率与所连接接收机基频信号的幅值对应，如两个基频信号的幅值单独调节时，则两个正对应负载直流功率的比值与调节后的幅值比值相一致。
[0080]
进一步地，对任一接收机，包括耦合电感线圈以及不可控整流器，耦合电感线圈的两端分别通过一接收机回路导线电阻、一接收调谐电容与所述不可控整流器适配连接，以通过所述不可控整流器与负载适配连接，以给所述负载提供所需的直流功率。
[0081]
图1中示出了接收侧包含n路接收机的情况，n路接收机一般可采用相同的形式，下面以图1中第一路接收机的情况进行举例说明，图1中，第一路接收机包括接收机回路导线电阻r
s1
，接收调谐电容c
s1
以及耦合电感线圈l
s1
，耦合电感线圈l
s1
的同名端与接收机回路导线电阻r
s1
的一端连接，耦合电感线圈l
s1
的非同名端与接收调谐电容c
s1
的一端连接，接收机回路导线电阻r
s1
的另一端以及接收调谐电容c
s1
的另一端均与不可控整流器(rectifler1)连接，通过不可控整流器为负载r
l1
提供直流功率，不可控整流器具体可以采用现有常用的形式，具体可以根据需要选择。
[0082]
第一路接收机的自然谐振频率由所述接收机内的接收调谐电容c
s1
以及耦合电感线圈l
s1
决定，其他路接收机的自然谐振频率与所述第一路接收机自然谐振频率的情况相一致，此处不再一一举例说明。具体实施时，其他路接收机的实施情况可以参考图1以及上述说明，此处不再一一列举说明。
[0083]
具体实施时，确定的系统基本参数包括接收机的期望谐振频率f
ei
(i＝1,2,...,n)、发射线圈l
p
的电感、接收线圈l
si
的电感(i＝1,2,...,n)、发射线圈l
p
与各耦合电感线圈l
si
间互感m
psi
(i＝1,2,...,n)、接收机负载r
li
(i＝1,2,...,n)以及接收调谐电容c
si
(i＝1,2,...,n)。
[0084]
本发明实施例中，对构建的多频多负载mcr-wpt系统，根据实际应用场景等情况，系统基本参数可以具体确定，此外，图1中的发射回路电阻r
p
为根据线路长度决定，接收机回路导线电阻也为根据线路长度决定阻值，负载电阻r
l1
等的阻值根据所接收机输出给的设备阻值决定。因此，待确定的参数即为上述lcl补偿拓扑网络内的发射谐振电感以及发射谐
振电容相对应的参数。
[0085]
进一步地，采用基波分析法确定所述多频多负载mcr-wpt系统的电路模型矩阵，并根据所确定的电路模型矩阵得到总反射阻抗频率特性曲线，其中，对所得到的总反射阻抗频率特性曲线，利用图解法得到所述多频多负载mcr-wpt系统的零相位工作频率。
[0086]
具体地，根据kcl(基尔霍夫电流定律)和kvl(基尔霍夫电压定律)进行，采用基波分析(fha，fundamental harmonic analysis)方法进行稳态分析，只考虑基波分量，而忽略直流分量或高次谐波。混频信号中各个不同频率的信号分别作为基波，将所述多频多负载mcr-wpt系统内看成相同数量的电路，各个电路中只存在一种对应频率的基波信号。
[0087]
本发明实施例中，采用基波分析法建立一对多通道mcr-wpt系统的等效电路，将原多频多负载mcr-wpt系统按功率通道分为多个单频多负载mcr-wpt系统来进行分析，每个单一系统由一个交流电压源驱动，所有单一系统均具有相同的电路结构。
[0088]
对基于基波分析法生成多频多负载mcr-wpt系统的电路模型矩阵，进行系统阻抗分析，计算出系统总输入阻抗z
in(i)
与系统工作频率fi之间的关系，以便可绘制系统输入阻抗角频率特性曲线。各接收机在发射侧的反射阻抗为z
rn(i)
，其计算公式如下：
[0089][0090]
其中，ωi表示系统实际工作角频率，m
ps1
，m
ps2
，...，m
psn
分别为发射线圈l
p
与各耦合电感线圈之间的互感，c
s1
，c
s2
，...，c
sn
分别为各接收机内接收调谐电容的电容值，l
s1
，l
s2
，...，l
sn
分别为各接收机内耦合电感线圈的线圈自感，r
s1
，r
s2
，...，r
sn
分别为各接收机内接收机回路导线电阻的阻值，r
eq1
，r
eq2
，...，r
eqn
分别为各接收机内不可控整流器与所接负载的等效电阻。
[0091]zr1(i)
为第一接收机在发射侧的反射阻抗，z
r2(i)
为第二接收机在发射侧的反射阻抗，其余类推，如z
rn(i)
为第n个接收机在发射侧的反射阻抗。在得到任一接收机在发射侧相应的反射阻抗后，根据电路理论，可计算出系统在工作频率fi下的输入阻抗为z
in(i)
。
[0092]
当工作频率为fi时，系统输入阻抗角θi计算公式为：θi＝arctan(im(z
in(i)
)/re(z
in(i)
))，基于此，可绘制出系统输入阻抗角频率特性曲线，通过对系统输入阻抗角频率特性曲线的分析，可以得出系统工作在零相位角(zero phase angle，zpa)的频率，即得到构建多频多系统mcr-wpt系统的实际谐振频率，从而实现利用图解法得到所述多频多负载mcr-wpt系统的零相位工作频率。所述工作频率为输入阻抗角为0
°
时，与系统输入阻抗角频率特性曲线相交点的频率，如图4所示。
[0093]
进一步地，根据零相位工作频率、系统基本参数以及目标工作频率构建适应度函
数为：
[0094][0095]
其中，fitness为所构建的适应度函数，f
ei
表示第i个接收机的期望谐振频率，f
si
为系统第i个实际谐振频率，即系统第i个零相位工作频率，i
si
为第i个接收机的负载电流，i
sj
为第j个接收机负载电流，k
si
为系统输入阻抗角频率特性曲线在第i个实际谐振频率点处的导数，k
sj
为系统输入阻抗角频率特性曲线在第j个实际谐振频率点处的导数，w1为谐振频率的寻优权重系数、w2为负载电流的寻优权重系数与w3为谐振点系统输入阻抗角频率特性曲线导数的权重系数。
[0096]
本发明实施例中，建立适应度函数fitness后，可进行寻优确定发射回路内lcl补偿拓扑网络的补偿网络参数。具体实施时，对第i个接收机期望谐振频率f
ei
，具体频率范围可为100khz-300khz，其中，第i个接收机的期望谐振频率f
ei
即为第i个接收机的目标工作频率，可根据接收机的数量分配期望谐振频率点。
[0097]
系统第i个实际谐振频率f
si
由图解法得出系统零相位工作频率点，一般地，当接收侧存在n个接收机时，且发射侧采用n-2路lc谐振回路与一lcl基本补偿网络依次适配连接时，则所述多频多负载mcr-wpt系统存在n个系统实际谐振频率。接收机的期望谐振频率根据需求预设确定，通过lcl补偿拓扑网络，可以得到系统总输入阻抗(所述系统具体是指构建的多频多负载mcr-wpt系统，即包含发射侧与接收侧)，图解法得到所述多频多负载mcr-wpt系统在满足zcs状态下的实际谐振频率，其中，实际谐振频率要尽可能靠近设计的期望谐振频率，以保证功率传输。
[0098]
具体实施时，谐振频率的寻优权重系数w1》负载电流的寻优权重系数w2≥谐振点输入阻抗角频率特性曲线导数的权重系数w3，如可分别设置为0.6，0.2，0.2。
[0099]
第i个接收机的负载电流i
si
为根据系统电路理论矩阵，由matlab解方程得出第i个接收机的负载电流；其他接收机的负载电流，可以采用相同的方式确定得到。根据系统输入阻抗频率特性曲线，在得出系统零相位工作频率工作点后，计算该点的导数，即得到在第i个实际谐振频率点处的导数k
si
，k
sj
的具体确定情况与在第i个实际谐振频率点处的导数k
si
类似，此处不再赘述。
[0100]
因此，对适应度函数fitness，具体可基于系统基本参数、目标工作频率、负载电流与谐振点输入阻抗角频率特性曲线导数构建得到。
[0101]
进一步地，对构建的适应度函数，基于pso方法寻优确定发射回路内lcl补偿拓扑网络的补偿网络参数，其中，确定补偿网络参数的过程包括如下步骤：
[0102]
步骤1、将发射回路内的发射谐振电感配置为电感粒子，将发射回路内的发射谐振电容配置为电容粒子，并确定第i个电感粒子l
fi
以及第i个电容粒子c
fi
相应的取值范围与运动速度范围，其中，i＝1,2,...,n-1；
[0103]
具体地，电感粒子l
fi
以及电容粒子c
fi
相应的取值范围与运动速度范围为：
[0104]
[0105][0106]
其中，vl
fi
为第i个电感粒子l
fi
的速度，vc
fi
为第i个电容粒子c
fi
相应的速度。
[0107]
步骤2、随机初始化电感粒子l
fi
以及电容粒子c
fi
；
[0108]
具体地，随机初始化时，电感粒子l
fi
以及电容粒子c
fi
相应的取值范围、运动速度范围需要在上述的取值范围内。
[0109]
步骤3、根据上述随机初始化后的电感粒子l
fi
以及电容粒子c
fi
，确定适应度函数的值，更新电感粒子l
fi
、电容粒子c
fi
相应的个体最佳适应度与群体最佳适应度；
[0110]
步骤4、根据上述更新电感粒子l
fi
、电容粒子c
fi
相应的个体最佳适应度与群体最佳适应度，更新电感粒子l
fi
、电容粒子c
fi
相对应的速度和位置，其中，
[0111][0112]
式中，l
mi
为电感粒子l
fi
个体最优粒子，y
lmi
为电感粒子l
fi
的群体最优粒子，li为电感粒子l
fi
当代种群所有粒子；c
mi
为电容粒子c
fi
个体最优粒子，y
cmi
为电容粒子c
fi
群体最优粒子，ci为电容粒子c
fi
当代种群所有粒子；β为惯性权重，λ1与λ2分别为自我学习因子和群体学习因子；rand为随机数产生器；
[0113]
具体地，通过步骤4的更新可得出下一代电感粒子与电容粒子。惯性权重β决定每一代电感粒子与电容粒子位置更新的幅度大小，决定适应度函数的收敛能力；自我学习因子λ1可调节电感粒子、电容粒子对自身最佳粒子的学习能力；群体学习因子λ2可调节电感粒子、电容粒子向群体最佳粒子学习的能力。一般地，惯性权重β一般设为0.9，自我学习因子λ1与群体学习因子λ2一般可均设置为1.2。
[0114]
具体实施时，在基于pso寻优时，将发射谐振电感、发射谐振电容的参数与系统基本参数代入到系统输入阻抗公式中，可以绘制系统输入阻抗角频率特性曲线，由系统输入阻抗角频率特性曲线可以得出构建多频多负载mcr-wpt系统的实际谐振频率以及相应实际谐振频率点处的导数。
[0115]
将发射谐振电感、发射谐振电容的参数与系统基本参数代入到电路矩阵模型中，可以计算出负载电流；由此，可以计算所构建适应度函数的值，即完成发射谐振电感、发射谐振电容到适应度的转化过程。
[0116]
例如，随机初始化100组电感粒子、电容粒子，每一个电感粒子、电容粒子都是一个个体，计算出每一组电感粒子、电容粒子对应的适应度并记录，作为个体最佳适应度，横向比较得出最低的适应度为群体最佳适应度，对应的这一组电感电容被记录为历史群体最佳粒子。
[0117]
根据速度和位置更新公式，得出下一代100组电感电容的值，再进行适应度计算，这一代适应度进行横向比较，得出当代最佳适应度，再与群体最佳适应度进行纵向比较，更新群体最佳适应度。
[0118]
步骤5、进行迭代次数控制，直至寻找到最佳适应度的电感粒子l
fi
与电容粒子c
fi
，以确定发射回路内lcl补偿拓扑网络的补偿网络参数。
[0119]
具体实施时，迭代次数一般可设为500次，若迭代完后，最佳适应度仍然较高，则继
续添加迭代次数，直至得出系统最佳适应度。具体实施时，最佳适应度最优为0，在具体实施时，计算得到的适应度值越靠近0越好，具体可以根据实际需要选择确定，以能满足实际的应用需求为准。
[0120]
本发明实施例中，在迭代次数的范围内，将最佳适应度值对应电感粒子、电容粒子相应的值作为发射谐振电感、发射谐振电容相应的取值，即实现利用pso寻优方式确定发射回路内lcl补偿拓扑网络的补偿网络参数。当然，具体实施时，还可以采用其他方式确定补偿网络参数的方式，具体可以根据需要选择。
[0121]
如图2所示，下面以一对二双频双负载mcr-wpt系统为例，来具体说明上述基于mfma叠加调制方法的多频多负载mcr-wpt系统及其参数设计过程，此时，接收侧包括两个接收机。
[0122]
具体地，构建双频双负载mcr-wpt系统，所构建的双频双负载mcr-wpt的具体情况可参考图2和上述说明，此处不再赘述。
[0123]
构建双频双负载mcr-wpt后，配置期望的传输频率：f
e1
＝180khz和f
e2
＝220khz，即一接收机的期望谐振频率为f
e1
＝180khz，另一接收机的期望谐振频率为f
e2
＝220khz。
[0124]
采用mfma叠加调制方法，将系统期望传输频率的正弦波信号在时域上进行叠加，得到包含这两种正弦波信息的混频信号，则有：
[0125][0126]
其中，ω1＝2πf
e1
，ω2＝2πf
e2
，max|y(t)|≤y
max
。
[0127]iin(i)
，i
p(i)
，i
s1(i)
，i
s2(i)
分别是系统输入电流，发射侧电流和接收机回路电流，其中，括号中的i代表开关频率fi(i＝1,2)。和是逆变器实际输出相对应频率的电压的有效值，则有：
[0128][0129]
不可控整流器与负载的等效负载r
eq1
和r
eq2
可以表示为：
[0130][0131]
利用kcl和kvl定理，建立如下的双频双负载mcr-wpt系统的电路模型矩阵，则有：
[0132][0133]
由上述说明可知，根据系统基本参数，接收机回路电流i
s1(i)
，i
s2(i)
可通过matlab求解，利用matlab求解得到接收机回路电流i
s1(i)
，i
s2(i)
的具体过程与现有相一致，为本技术领域人员所熟知，此处不再赘述。具体实施时，对于多频多负载mcr-wpt系统，接收机回路
电流的具体情况，可以参考此处双频双负载mcr-wpt系统的求解确定过程，具体为本技术领域人员所熟知。
[0134]
采用基波分析法建立双频双负载mcr-wpt系统的等效电路，将原双频mcr-wpt系统按功率通道分为两个单频多负载mcr-wpt系统来进行阻抗分析，如图3所示；此时，接收机在发射侧的反射阻抗为z
r1(i)
和z
r2(i)
，公式如下：
[0135][0136]
因此，双频双负载mcr-wpt系统在某一工作频率fi时的输入阻抗z
in(i)
可以表示为：
[0137][0138]
利用matlab绘制并分析系统输入阻抗角频率特性曲线，得出系统的实际谐振频率与实际谐振频率点处的导数。
[0139]
上述给出了根据在发射侧的反射阻抗z
r1(i)
和发射侧的反射阻抗z
r2(i)
，确定对应的双频双负载的输入阻抗z
in(i)
的方式以及过程，对于多频多负载确定工作频率fi时的输入阻抗z
in(i)
的情况，可以参考此处说明，具体为技术领域人员所熟知，此处不再赘述。
[0140]
图4中为系统输入阻抗角频率特性曲线，图4中纵坐标为输入阻抗角频率，横坐标为输入频率；图5为系统输入阻抗频率特性曲线，图5中纵坐标为输入阻抗，横坐标为输入频率。由图4和图5，即可得到双频双负载mcr-wpt系统相应的实际谐振频率。
[0141]
设置双频双负载mcr-wpt系统的系统基本参数，如下表所示：
[0142] 电参数v
in
100vl
p
100μhl
s1
100μhl
s2
100μhc
s1
8nfc
s2
5nfr
l1
10ωr
l2
10ωm
ps1
50μhm
ps2
50μh
[0143]
在设置系统基本参数之后，选取剩余的发射侧lcl补偿拓扑网络内发射谐振电感lf与发射谐振电容c
p
作为pso算法的待优化量，确认期望谐振频率、接收机回路电流与谐振点输入阻抗角频率特性曲线导数为寻优目标。
[0144]
以期望谐振频率为主寻优目标，设置w1为谐振频率的寻优权重系数、w2为负载电流
的寻优权重系数与w3为谐振点输入阻抗角频率特性曲线导数的权重系数分别为0.6，0.2，0.2。构建的适应度函数为：
[0145]
fitness＝w1(|f
s1-f
e1
|2+|f
s2-f
e2
|2)+w2|i
s1-i
s2
|2+w3|k
s1-k
s2
|2[0146]
采用pso寻优方式时，最后的寻优结果具体为：
[0147]
lf＝72μh，c
p
＝10nf，f
s1
＝180.7khz,f
s2
＝211.5khz。
[0148]
综上，通过上述给出了双频双负载mcr-wpt系统以及具体设计方法的设计过程，其他情况设计情况可以参考上述说明。
[0149]
通过调节输入端各频率归一化电压幅值，两负载电压如图6～图8所示。图6中，一接收机输出的负载电压u
l1
为16.08v、另一接收机输出的负载电压u
l2
为15.95v，此时，基频信号对应的幅值a1＝a2＝1。图7中，为a1＝1.5，a2＝0.5，此时，一接收机输出的负载电压u
l1
为22.57v、另一接收机输出的负载电压u
l2
为8.375v；图8中，为a1＝1，a2＝0.8，此时，一接收机输出的负载电压u
l1
为15.55v、另一接收机输出的负载电压u
l2
为12.44v。
[0150]
对两接收机输出的电压进行fft(fast fourier transform)分析，如图9～图11所示。由图示可知，系统输出电压变化与对应频率归一化电压幅值一致，即基频信号的幅值决定对应接收机所接收频率信号的大小，可以决定输出给负载的功率电压大小。
[0151]
在matlab中，利用fft分析工具对接收机输出电压进行fft分析，其横坐标为频率，纵坐标为各频率在该信号中的分量；matlab中fft分析工具对电压具体进行fft分析的方式以及过程均与现有相一致。图9中，接收机输出电压包含上述系统实际谐振频率f
s1
与系统实际谐振频率f
s2
频率分量，其比例与基频幅值a1＝a2＝1相对应的比值相同。图10中，接收机输出电压包含上述f
s1
与f
s2
频率分量，其比例与基频幅值a1＝1.5，a2＝0.5相对应的比值相同。图11中，接收机输出电压包含上述f
s1
与f
s2
频率分量，其比例与基频幅值a1＝1，a2＝0.8相对应的比值相同。
[0152]
以上实施例仅是为充分说明本发明而所举的较佳的实施例，本发明的保护范围不限于此。本技术领域的技术人员在本发明基础上所作的等同替代或变换，均在本发明的保护范围之内。本发明的保护范围以权利要求书为准。