一种储能装置等效虚拟惯性时间常数计算方法

1.本发明涉及电力系统动态频率特性分析技术领域，具体涉及一种储能装置等效虚拟惯性时间常数计算方法。


背景技术：

2.利用电化学储能装置的快速功率调节能力，参与系统频率调节，是储能的重要应用技术之一。近年来，随着新能源大力发展，系统惯量水平不断降低。储能装置通过附加虚拟惯性控制，改变其输出有功功率释放能量进行惯性响应，从而提高系统惯量水平，改善系统动态频率特性。储能主动参与系统惯性响应，使系统等效惯性时间常数由已知变得未知，系统动态频率特性也将发生变化。定量表征储能惯性响应能力，计算储能虚拟惯性时间常数表达式是研究上述问题的关键。当前，尚未获得储能虚拟惯性时间常数的完整表达结果。


技术实现要素：

3.本发明提出一种储能装置等效虚拟惯性时间常数计算方法，通过计算储能装置等效虚拟惯性时间常数，为进一步研究含储能虚拟惯性控制的电力系统动态频率特性等相关问题奠定了重要基础。
4.本发明采取的技术方案为：
5.一种储能装置等效虚拟惯性时间常数计算方法，包括以下步骤：
6.步骤1：引入典型微分惯性控制方法，定义储能装置虚拟惯性时间常数表达式：
[0007][0008]
式中：ωe、
△
ωe分别为电力系统同步角速度、角速度变化量；ub、sb分别为储能装置的额定电压、额定容量；qn为储能装置满充状态下的额定电量；
△
γ
soc
′
为储能装置的荷电状态变化率；
[0009]
典型微分惯性控制方法通过引入电网频率微分信号，根据频率变化率和惯性控制增益大小，产生有功功率参考值和功率响应，执行储能惯性控制。微分惯性控制下，储能装置具备惯性响应能力，在此前提下可定义储能装置的虚拟惯性时间常数表达式。
[0010]
步骤2：根据步骤1定义的储能装置虚拟惯性时间常数表达式可知，若要定量求解h
bess
，须进一步求解间的比值关系；
[0011]
步骤3：根据步骤2得到代入步骤1，进而计算h
bess
的复频域值；
[0012]
步骤4：带入相关参数，通过拉普拉斯反变换计算得到h
bess
的时频域值。
[0013]
相关参数具体指下面式(8)中的参数，包括控制器增益k
df
，储能装置的额定电压ub，额定容量sb，储能并网侧电压直轴分量ud，电力系统同步角速度ωe以及滤波器时间常数t1、t2。
[0014]
所述步骤2中，储能装置的荷电状态变化率与电力系统同步角速度变化量之比的表达式为：
[0015][0016]
式(6)中：k
df
为微分惯性控制器增益；t1、t2为滤波器时间常数；ud为储能并网侧电压直轴分量；s为复频域计算符。
[0017]
式(6)中5400是结合储能逆变器控制模型计算所得，具体可参考说明书附图中的图4，1/5400＝(1/3600)*(2/3)，其中的3600为模型中小时与秒间的转换单位，2/3为储能逆变器有功功率参考值与d轴参考电流的关系表达式的系数。
[0018]
所述步骤3中，所述h
bess
的复频域值表达式为：
[0019][0020]
式(7)中5400是结合储能逆变器控制模型计算所得，具体可参考说明书附图中的图4，1/5400＝(1/3600)*(2/3)，其中的3600为模型中小时与秒间的转换单位，2/3为储能逆变器有功功率参考值与d轴参考电流的关系表达式的系数。
[0021]
所述步骤4中，所述h
bess
的时频域值表达式为：
[0022][0023]
其中：
[0024]
式(8)中：为常数，k1、k2为拉氏反变换部分分式展开式的系数，ωe为电力系统同步角速度。
[0025]
k的参数表达式中，10800根据式(7)中5400*2得来，为式(6)代入步骤1中储能h
bess
的定义式计算所得。
[0026]
本发明一种储能装置等效虚拟惯性时间常数计算方法，技术效果如下：
[0027]
1)本发明在储能装置附加微分惯性控制的前提下，计算储能等效虚拟惯性时间常数，与同步机组具有恒定惯性时间常数不同的是，本发明中储能虚拟惯性时间常数具有明显的动态时变特性，计算结果精确性较高。
[0028]
2)本发明中储能装置等效虚拟惯性时间常数具有明显的动态时变特性，与同步机组具有恒定惯性时间常数的特征存在显著差异。本发明为进一步研究含储能虚拟惯性控制的电力系统动态频率特性奠定了重要基础。
附图说明
[0029]
图1为本发明实施例的流程图。
[0030]
图2为储能装置虚拟惯性控制模型图。
[0031]
图3为储能装置逆变器控制模型图。
[0032]
图4为含虚拟惯性控制的储能装置传递函数模型图。
[0033]
图5为独立微电网结构示意图。
[0034]
图6为储能装置虚拟惯性时间常数计算值与仿真值对比图。
具体实施方式
[0035]
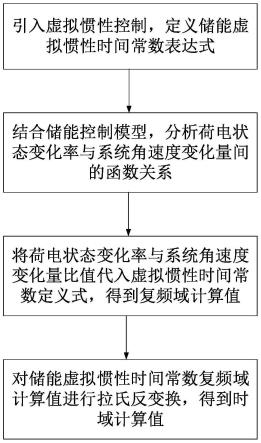
一种储能装置等效虚拟惯性时间常数计算方法，在储能附加微分惯性控制下，定义储能虚拟惯性时间常数，并通过分析定量表征其值。结合储能逆变器控制模型，探讨惯性响应过程储能荷电状态变化率与系统同步角速度变化量间的比值关系，将其代入储能虚拟惯性时间常数定义式，得到惯性时间常数的复频域表达式，再经拉氏反变化得到时域值，最后通过算例系统，验证了储能虚拟惯性时间常数计算的精确性。本发明实施的具体流程图如图1所示，包括以下步骤：
[0036]
步骤1：将储能装置在频率响应过程中释放的能量，表示为与同步发电机旋转动能相似的形式，得到：
[0037][0038]
式(1)中：ub、ib(t)、γ
soc
、qn分别为储能装置的额定电压、放电电流、荷电状态及满充状态下的额定电量；sb为储能装置额定容量；pn、j
vir_b
分别为等效同步发电机的极对数、虚拟转动惯量；ωe为电力系统同步角速度。
[0039]
由上式可得：
[0040][0041]
进一步得到储能虚拟惯性时间常数定义式：
[0042][0043]
式(3)中：
△
ωe为电力系统角速度变化量；
△
γ
soc
′
为储能装置的荷电状态变化率。
[0044]
步骤2：为定量求解h
bess
，需进一步讨论间的比值关系，结合图2的储能装置虚拟惯性控制模型，可得：
[0045][0046]
根据图3的储能装置逆变器控制模型，可得储能逆变器有功功率参考值与d轴参考
电流的关系表达式如下所示：
[0047][0048]
进一步分析得到储能荷电状态变化率和同步角速度变化量的关系如图4所示，由图4可得：
[0049][0050]
上式中：k
df
为微分惯性控制器增益；t1、t2为滤波器时间常数；ud为储能并网侧电压直轴分量；s为复频域计算符。
[0051]
步骤3：由步骤2中的计算结果，代入步骤1中h
bess
的定义式，可得h
bess
的复频域表达式：
[0052][0053]
式(7)中，可设k＝ubωe/(10800udsb)，通过分析可知，分母多项式的判别式
△
≥0，即分母多项式有两个单根。
[0054]
步骤4：对步骤3中h
bess
的复频域表达式进行拉普拉斯反变换，得到h
bess
时域表达式：
[0055][0056]
式(8)中：
[0057]
在matlab/simulink环境下，搭建如图5所示的独立微电网系统模型，验证h
bess
(t)计算结果正确性，微电网系统中电源配置容量及参数如表1所示。
[0058]
表1微电网配置
[0059][0060]
t＝15s时，设置突增负荷l2，模拟系统功率缺额下的频率扰动。比较储能装置频率响应动态过程中h
bess
(t)的计算值与仿真值，如图6所示。其中，h
bess
(t)仿真值通过提取储能虚拟惯性响应过程中
△
γ
soc
′
/
△
ωe，并带入式(3)中计算得到，h
bess
(t)计算值，由式(8)并代入相关参数获得。
[0061]
从图6可以看出，按照本发明所定义、推导计算获得的h
bess
(t)值与仿真值总体较为吻合，表明h
bess
(t)计算值精确性较高。此外，图6中的h
bess
(t)曲线具有明显的动态时变特性，与同步机组具有恒定惯性时间常数的特征存在显著差异，为进一步研究含储能虚拟惯
性控制的电力系统动态频率特性奠定了重要基础。